Journal of Applied Mathematics and Physics
Vol.02 No.08(2014), Article ID:47947,8 pages
10.4236/jamp.2014.28092
Curvature Motion on Dual Hyperbolic Unit Sphere 
Ziya Yapar, Yasemin Sağıroğlu*
Karadeniz Technical University, Trabzon, Turkey
Email: *sagiroglu.yasemin@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 1 June 2014; revised 1 July 2014; accepted 13 July 2014

ABSTRACT
In this paper, we define dual curvature motion on the dual hyperbolic unit sphere 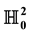 in the dual Lorentzian space
in the dual Lorentzian space 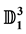 with dual signature
with dual signature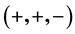 . We carry the obtained results to the Lorentzian line space
. We carry the obtained results to the Lorentzian line space  by means of Study mapping. Then we make an analysis of the orbits during the dual hyperbolic spherical curvature motion. Finally, we find some line congruences, the family of ruled surfaces and ruled surfaces in
by means of Study mapping. Then we make an analysis of the orbits during the dual hyperbolic spherical curvature motion. Finally, we find some line congruences, the family of ruled surfaces and ruled surfaces in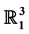 .
.
Keywords:
Dual Curvature Motion, Dual Lorentzian Space, Study Mapping

1. Introduction
Dual numbers had been introduced by W.K. Clifford (1845-1849) as a tool for his geometrical investigations. After him, E. Study (1860-1930) used dual numbers and dual vectors in his research on the geometry of lines and kinematics [1] . He devoted special attention to the representation of directed lines by dual unit vectors and defined the mapping that is known by his name. There exists one-to-one correspondence between the vectors of dual unit sphere 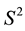 and the directed lines of space of lines
and the directed lines of space of lines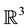 . Hence, a differentiable curve on the sphere
. Hence, a differentiable curve on the sphere 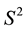 corresponds to a ruled surface in the line space
corresponds to a ruled surface in the line space 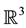 [2] - [4] . Ruled surfaces have been widely applied in surface design, manufacturing technology and simulation of rigid bodies [5] .
[2] - [4] . Ruled surfaces have been widely applied in surface design, manufacturing technology and simulation of rigid bodies [5] .
E. Study’s mapping plays a fundamental role in the real and dual Lorentzian spaces [6] . By this mapping, a curve on a dual hyperbolic unit sphere 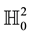 corresponds to a timelike ruled surface in the Lorentzian line space
corresponds to a timelike ruled surface in the Lorentzian line space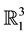 , in other words, there exists a one-to-one correspondence between the geometry of curves on
, in other words, there exists a one-to-one correspondence between the geometry of curves on 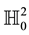 and the geometry of timelike ruled surfaces in
and the geometry of timelike ruled surfaces in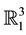 . Similarly, a timelike (spacelike) curve on a dual Lorentzian unit sphere
. Similarly, a timelike (spacelike) curve on a dual Lorentzian unit sphere 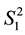 corresponds to a spacelike (timelike) ruled surface in the Lorentzian line space
corresponds to a spacelike (timelike) ruled surface in the Lorentzian line space , this means that, there exists a one-to-one correspondence between the geometry of timelike (spacelike) curves on
, this means that, there exists a one-to-one correspondence between the geometry of timelike (spacelike) curves on 





Real spherical curvature motion had been introduced by A. Karger and J. Novak [8] . Also, a dual spherical curvature motion has been defined by Z. Yapar [9] . In recent years, study about the real spherical motion has been generalized to the Lorentz spherical motion [6] [7] [10] [11] . In this work, we consider the curvature motion on the dual hyperbolic unit sphere 

2. Preliminaries and Definitions
In this section, we give a brief summary of the theory of dual numbers, dual Lorentzian vectors and Study’s mapping.
Let 


where 

A vector 






The norm of a vector 



tors in


If 




The set of all dual numbers forms a commutative ring over the real numbers field and is denoted by 𝔻. Then the set
is a module over the ring 𝔻 which is called a 𝔻-module or dual space. The elements of 

where 


If 


Let 


where 

The norm 

Then we can write
The Lorentzian inner product of two dual vectors

where 



A dual vector 


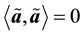
where 

The set of all dual Lorentzian vectors is called dual Lorentzian space and it is denoted by
The Lorentzian cross product of dual vectors 

where 

Lemma 2.1. Let
1)
2) 

3) 
4) 
Let





The set of all dual timelike unit vectors (resp., all dual spacelike unit vectors) is called the dual hyperbolic unit sphere (resp., dual Lorentzian unit sphere) and is denoted by 

Theorem 2.2. (E. Study Map) [6] There exists one-to-one correspondence between directed timelike (resp., spacelike) lines of 




Definition 2.1. A directed timelike line in 




is called the moment of the vector 
This means that the direction vector 




Let


and
[7] . In this case the orthonormal system 

A ruled surface is a surface generated by the motion of a straight line in
Definition 2.2. A ruled surface is said to be timelike if the normal of surface at every point is spacelike, and spacelike if the normal of surface at every point is timelike [7] .
Let 

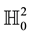








3. Dual Curvature Motion on the Dual Hyperbolic Unit Sphere
Let us consider a fixed dual orthonormal frame 














endpoints of segment 











where the vector 


where 

i.e. 




Thus, we have the orthonormal dual frame






Denote the dual hyperbolic angles of 



where 



where 








Let 



Since 



and

If





From Equation (9) we have

which represents a line congruence. Thus, we have the following theorem.
Theorem 3.1. During the dual hyperbolic spherical curvature motion 
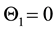




If we take 

Thus, we have the following theorem.
Theorem 3.2. During the dual hyperbolic spherical curvature motion 




In addition, if we take 
which represents a right helicoid.
If





If we put

From Equation (14) we have

which represents a cone whose axis is the vector
Theorem 3.3. During the dual hyperbolic spherical curvature motion, the orbit drawn on 




If we put

From Equation (16) we have

which represents a cone whose axis is the vector
Theorem 3.4. During the dual hyperbolic spherical curvature motion, the orbit drawn on 




4. Analysis of the Orbit of 
Seperating real and dual parts of


Equations (18) and (19) have only two parameters 






Since 


In the case of 

From Equation (22) we obtain

which represents an one-parameter family of cone in
If we put 

which represents an elliptic cone, whose axis is the vector
Theorem 4.1. During the dual hyperbolic spherical curvature motion, the orbit drawn on 




In addition, putting various values of parameters in the Equations (21) or (22) we have different line congruences or ruled surfaces in
5. Conclusion
This paper presents the curvature motion on the dual hyperbolic unit sphere




References
- Study, E. (1903) Geometrie der Dynamen. Mathematiker Deutschland Publisher, Leibzig.
- Guggenheimer, H.W. (1963) Differential Geometry. McGraw-Hill, New York.
- Hacısalihoğlu, H.H. (1972) On the Pitch of a Closed Ruled Surface. Mechanism and Machine Theory, 7, 291-305. http://dx.doi.org/10.1016/0094-114X(72)90039-0
- Veldkamp, G.R. (1976) On the Use of Dual Number, Vector and Matrices in Instantaneous Spatial Kinematics. Mechanism and Machine Theory, 11, 141-156. http://dx.doi.org/10.1016/0094-114X(76)90006-9
- Zha, X.F. (1997) A New Approach to Generation of Ruled Surfaces and Its Application in Engineering. The Interna- tional Journal of Advanced Manufacturing Technology, 13, 155-163. http://dx.doi.org/10.1007/BF01305867
- Uğurlu, H.H. and Çalışkan, A. (1996) The Study Mapping for Directed Spacelike and Timelike Line in Minkowski 3-Space
. Mathematical and Computational Applications, 1, 142-148.>http://html.scirp.org/file/12-1720166x306.png" class="200" />. Mathematical and Computational Applications, 1, 142-148.
- Yaylı, Y., Çalışkan, A. and Uğurlu, H.H. (2002) The E Study Maps of Circles on Dual Hyperbolic and Lorentzian Unit Spheres
and
and
. Mathematical Proceedings of the Royal Irish Academy, 102A, 37-47.>http://html.scirp.org/file/12-1720166x308.png" class="200" />. Mathematical Proceedings of the Royal Irish Academy, 102A, 37-47.
- Karger, A. and Novak, J. (1985) Space Kinematics and Lie Groups (Translated by Michal Basch). Gordon & Breach, New York.
- Yapar, Z. (1989) On the Curvature Motion. Communications, Faculty of Sciences, University of Ankara, Series A1, 38, 103-114.
- Uğurlu, H.H., Çalışkan, A. and Kılıç, O. (2001) On the Geometry of Spacelike Congruence. Communications Faculty of Sciences, University of Ankara, Series A1, 50, 9-24.
- Kazaz, M., Özdemir, A. and Uğurlu, H.H. (2009) Elliptic Motion on Dual Hyperbolic Unit Sphere
. Mechanism and Machine Theory, 44, 1450-1459. >http://html.scirp.org/file/12-1720166x309.png" class="200" />. Mechanism and Machine Theory, 44, 1450-1459. http://dx.doi.org/10.1016/j.mechmachtheory.2008.11.006
- Çalışkan, A., Uğurlu, H.H. and Kılıç, O. (2003) On the Geometry of Timelike Congruence. Hadronic Journal Supple- ment, 18, 311-328.
- Akutagawa, K. and Nishikawa, S. (1990) The Gauss Map and Spacelike Surfaces with Prescribed Mean Curvature in Minkowski 3-Space. Tohoku Mathematical Journal, 42, 67-82. http://dx.doi.org/10.2748/tmj/1178227694
- Birman, G.S. and Nomizu, K. (1984) Trigonometry in Lorentzian Geometry. American Mathematical Monthly, 91, 543-549. http://dx.doi.org/10.2307/2323737
- O’Neil, B. (1983) Semi-Riemannian Geometry with Applications to Relativity. Academic Press, London.
- Yaglom, I.M. (1979) A Simple Non-Euclidean Geometry and Its Physical Basis. Springer-Verlag, New York.
NOTES
*Corresponding author.




























 . Mathematical and Computational Applications, 1, 142-148.>http://html.scirp.org/file/12-1720166x306.png" class="200" />. Mathematical and Computational Applications, 1, 142-148.
. Mathematical and Computational Applications, 1, 142-148.>http://html.scirp.org/file/12-1720166x306.png" class="200" />. Mathematical and Computational Applications, 1, 142-148. and
and and
and . Mathematical Proceedings of the Royal Irish Academy, 102A, 37-47.>http://html.scirp.org/file/12-1720166x308.png" class="200" />. Mathematical Proceedings of the Royal Irish Academy, 102A, 37-47.
. Mathematical Proceedings of the Royal Irish Academy, 102A, 37-47.>http://html.scirp.org/file/12-1720166x308.png" class="200" />. Mathematical Proceedings of the Royal Irish Academy, 102A, 37-47. . Mechanism and Machine Theory, 44, 1450-1459. >http://html.scirp.org/file/12-1720166x309.png" class="200" />. Mechanism and Machine Theory, 44, 1450-1459.
. Mechanism and Machine Theory, 44, 1450-1459. >http://html.scirp.org/file/12-1720166x309.png" class="200" />. Mechanism and Machine Theory, 44, 1450-1459. 