Open Journal of Philosophy
Vol.06 No.01(2016), Article ID:64011,20 pages
10.4236/ojpp.2016.61012
Structures of Confinements as an Empirical Property of Consciousness and a Fundamental Property in Physics
Nikolai Lyng
Moss, Norway

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 January 2016; accepted 26 February 2016; published 29 February 2016
ABSTRACT
Our consciousness is confined to experience our own thoughts. By subjectively investigating associations between conscious experiences from different senses, it can be shown how confinement must be an existing property relating to smaller parts of our conscious experiences as well. In this article, it is investigated how entities confining other entities may serve as fundamental building blocks of physics and consciousness. The model evolves by changing the structure of confinements. It turns out that classical mechanics, relativity, quantum mechanics, non-locality, and a solution to the measurement problem in quantum mechanics follow from the definition of this model. The model also clarifies how different conscious experiences can be determined by different physical states, which is related to the hard problem of consciousness.
Keywords:
Consciousness, Ontology, Confinement, Entities, Modeling Physics

1. Introduction
If consciousness is fundamental, it means that objective reality exists in the same way which consciousness exists. Is it necessary with more than one possible explanation for how existence generally occurs? In order to understand how consciousness can be fundamental, we will identify further properties related to consciousness. We do not experience somebody else’s experiences and we are confined to only experience our own conscious experiences. Therefore, confinement is a property which relates to our consciousness. It will also be shown how confinement of other confinements is a fundamental property within our conscious experiences as well.
In this article, I will model physics in terms of entities confining other entities. The model evolves by changing its structure of confinements. It will be shown how classical mechanics, relativity, charge, quantum mechanics and a solution to the measurement problem in quantum mechanics are mathematical consequences that follow from the definition of this model.
2. Generalizing Structures of Confinements
If consciousness is fundamental, then structures of confinements must be fundamental as well. That which is fundamental can be generalized to explain those concepts which are less fundamental. As such we will identify possible fundamental explanations for how we relate to numbers, what information is and quantum mechanics. While the property of confinement does not explain what conscious experience is, it can tell us something about how conscious experience is subject to change. This will be relevant to understand how physical states in the brain can possibly determine different conscious experiences.
2.1. The Concept of Fundamental
If you have a bottle, you can say that this bottle consist of molecules. Then, molecules are the more fundamental concept. That is because we can explain a bottle in terms of molecules, but we cannot explain molecules in terms of bottles.
If you have a more fundamental understanding of something, you are likely to be able to find more information due to generalization. By generalizing this fundamental concept, you can predict more. For example, by identifying the more fundamental concept of molecules we can predict chemistry. Chemistry can be generalized to explain properties of objects.
The concept of fundamental is only relevant to how we mentally categorize how basic we predict the objective reality, but is not otherwise really a property of the objective reality itself. In reality what we perceive as a bottle, is neither molecules nor a bottle, we don’t even know what it truly is.
2.2. Symmetry and Generalization
In physics, the most fundamental way of explaining information is by the concept of symmetry. To observe a symmetry is to observe that something is similar while something else is different (Obviously the property of difference is required to not be the exact same thing). For example, if I am observing that a ball always falls each and every time I drop it, I assume that it will fall the next time as well. All the laws of physics and knowledge can be described in terms of symmetry. The same goes for formulas due to the equality sign.
If two things have one similarity, it is at least somewhat more probable that they have more similarities in common. That is because causes which are similar often create results which are similar. Perhaps one way we can understand it is due to that cause and effect can be considered a transformation, where certain similarities survive the transformation. This is why evolution has found it constructive to give us the ability to generalize. Most likely our brain can be categorized into similar areas, because they are generalizing similar type of information. E.g. sight perception is related to information from electromagnetic waves (similar cause is the different electromagnetic waves), and emotions to particular contexts (similar cause is the different situations defining the context) and so on. Despite that generalizing to find a conclusion often isn’t reliable, it is undeniably fundamental. Every time we learn something new, it is based on generalization. Similarities observed at a more fundamental level often have fewer possible causes. This results in that generalization becomes more reliable. It is most likely the reason why the concept of symmetry is commonly taught in particle physics, which is because particles are fundamental. As an example how things are simpler at a fundamental level consider that molecules can result in what we can label as an infinite amount of objects (less fundamental and more complex). However at a more fundamental level, we know that all molecules consist of protons, electrons and neutrons (more fundamental and simpler). We see that generalizing and saying that the fundamental concept of particles constitutes three dimensional objects will be correct. Generalization is that which compensates for that fundamental knowledge is simpler.
Let us look at an example of how according to a book in particle physics the concept of symmetry explains conservation of momentum: “Invariance under translation in space implies conservation of momentum.” Here invariance implies the similarity. Translation in space is what I earlier referred to as “transformation”, or “difference”. That momentum is always conserved implies the generalization.
Any observation we make is the result of particles interacting with each other. That includes light which consists of photons interacting with other particles. In order to go beyond what we can observe, e.g. identifying properties inside particles, the concept of symmetry is used in particle physics. We will use the same concept to investigate our consciousness and its relation to the objective reality. Then we will see how harmoniously the generalizations fit into the laws of physics.
2.3. Consciousness and Structure of Confinements
I would like to show that a basic property of consciousness is confinement and containment. In this case the word containment refers to that confinements can confine other confinements. Our consciousness is that which is conscious of our mental experiences. Try to notice that some thoughts seem to be distinguishable from others, while we perceive that some are more related. This is really a general property of our thoughts within our consciousness. For example if you imagine a house built of bricks, aren’t the bricks somehow more related to each other, than they are to another perception of for example a river? Notice that the property of confinement has this same property. It relates to what it confines and is not related to what it doesn’t confine.
Let us consider a group of three marbles. Notice that you now associate the word “group” with the three marbles. If I would ask anybody why, they would most likely say that it is because it is a property of the brain to make us associate them together, and that is true. However what also happens to be true is that the relation between the word “group” and the three marbles occurs entirely within the realm of our conscious experiences as well. The word “group” is an existing thought, and the perceptions of marbles are existing thoughts as well. This means that the relation between the word “group” and the three marbles truly exists as well. Since the word “group” relates to all the three marbles in the same way, we can refer to it as the property of confinement.
Imagine two marbles. We can refer to one of them as “marble 1” and the other as “marble 2”. The marble referred to as marble 1 has a scent of chocolate, while marble 2 does not. Let us further refer to the collection of both of the marbles as the word “group”. In this example we can observe the property of containment, which is confinement of confinements. Within our conscious experience, the word “group” relates to both marble 1 and marble 2 resulting in a confinement of the two marbles. Another confinement within this confinement is how marble 1 is confined together with the perception of the scent of chocolate and that marble 2 is excluded from this confinement. Something confines marble 1 and marble 2. Something else confines only marble 1 and the scent of chocolate.
Let us from now define that which confines or contains as a unified entity. The word “unified” is chosen to indicate the property of confinement and the word “entity” implies that it exists. I will clarify more why unified entities exist in a later chapter. Every thought within our consciousness can be explained in terms of unified entities. We can investigate random thoughts within our consciousness to see that unified entities represent a fundamental property of any thought.
For example a thought about a laptop can be considered a unified entity confining the mental picture of the laptop and the word “laptop”. Within our perception of the laptop, we can discover that it consist of more objects such as buttons. The buttons can be related to the word “button” and our perception of buttons can be considered as separate from the screen and the word “screen”. In other words, the buttons are more related to the word “button” than to the word “screen”. Still the word button and screen are confined by our perception of the laptop and more related to the perception of laptop than any other random thought which is not a part of the laptop. We can explain this as such. The thought of a laptop is a unified entity containing a unified entity which contains the word screen and the mental picture area of the screen, and another unified entity containing the word “button” and the mental picture of a button on the laptop. In other words our conscious experiences consist of objects containing other objects. This structure of containment is fundamental in our consciousness.
What about music? It is conscious mental experience. Objectively speaking, music and variation of tones occur only in the “now”. How long is now? It is perhaps shorter than the shortest time you can imagine. Yet while we listen to music, we perceive tones in our conscious experiences that are long enough to be counted in units of time, and even sequences of different tones. This in itself implies that our consciousness relates sequences of tones together in terms of confinement. In fact, we cannot enjoy music nor relate it to any emotion without perceiving that it consists of more than one tone. As such a unified entity confines many tones together including their associated emotion.
Even the shape of a mental picture defines a structure based on confinement. If you imagine a mental picture of a cup it has a shape. This implies that each point in the shape has a relative position to any other point on the shape. As such each point on the shape must be confined from another point. We can distinguish between different parts of the shape. Yet our brain is not structured to let us associate with those confinements responsible for defining the relative positions in a mental picture. In the chapter called “foundational layers of confinement” we will see an example of how a structure of unified entities can define relative positions.
Until now we have observed the property of connection as confinement or containment and generalized it to assume that it is a property describing any of our thoughts. It can be subjectively observed in our consciousness that any thought may relate to other thoughts due to the property of confinement.
2.4. What Is Our Consciousness?
In the previous chapter we defined unified entities to be that which contains and confines, such that one unified entity can confine other unified entities. This property of confinement defines a connection between what it confines. What about our consciousness itself, is it very different from how we defined a unified entity?
Our whole consciousness consists of many thoughts. In other words, our consciousness contains all of our thoughts. My consciousness and somebody else’s are different because I do not directly experience another person’s thoughts. Thus I am somehow confined into my own existence and perceptions. We see that our consciousness itself has the exact same property as unified entities. They both have the property of confinement.
If you recall the chapter called “symmetry and generalization”, we concluded that similar causes tend to produce similar results. Also if the concepts are fundamental, generalization becomes more reliable. Our consciousness is undoubtedly fundamental since it is the very process of existence itself. If there is a similar cause behind why our consciousness exists and has the property of containment and why our individual thoughts exist and has the property of containment, it can be worthwhile to hypothetically generalize properties between our thoughts, and our consciousness. What if our individual thoughts are individual consciousness? That would imply that each unified entity is confined due to observing its contents just like our consciousness. The generalization of assuming that consciousness is a unified entity is necessary in order to generalize cause and effect in a later chapter.
2.5. Confinement and Existence
I would like to emphasize the strong foundation unified entities have in reality. Let us find yet another example to subjectively observe the very existence of unified entities within our consciousness. Imagine a cup, and that you associate the word “cup” with the mental picture of the cup. What makes you experience the word “cup” as related to the mental picture of the cup? There is no other reason than that these two existing thoughts are somehow related to each other in a way that they are not related to any other thoughts. Since these two thoughts exist, then the relation between them must exist as well, since if it did not exist, nothing could relate these existing thoughts together. This relation defines a confinement. Therefore unified entities must exist as the cause behind this relation between thoughts.
One could argue that the property of confinement doesn’t exist, but is just a way of observing, or a perspective caused by observation. The response to such a claim is that whether it is a property of the observer or a property of the individual thoughts, or both, there is no denying that the mechanism of confinement occurs and that we have observed it to be a fundamental property describing any thought. Furthermore if it is a property of the observer or a property of perspective, it still exists, because we as observers exist.
2.6. A Fundamental Explanation of Numbers
Numbers were first defined as elements containing other elements. Later this definition was abandoned, due to a contradiction. It was replaced with modern set theory, where a set is a collection of elements, but the set is not an element itself.
What is interesting here is that the concept of unified entities itself is a fundamental explanation of how numbers exist and is more similar to the properties of older set theory. Both unified entities and older set theory have the property, that one element contains other elements. We have already observed that unified entities contain other unified entities. Since unified entities are fundamental, the origin of numbers is due to the existence of unified entities. Each unified entity is then one unit. Units can be counted and thus follow the rules of mathematics. Older set theory was claimed to be disproved. However this disproof cannot be applied to unified entities without being based on an overgeneralization. Below is the contradiction of older set theory.
So let us look at the so called contradiction which disproved the older version of set theory. The contradiction is as follows: If one defines the element containing only all elements which do not contain themselves. Then if this element does not contain itself, it does not contain all elements which don’t contain themselves, which would be a contradiction. If it contains itself it would be a contradiction as well.
If applied to unified entities, the overgeneralization occurs by claiming the necessity of the existence of “an element containing only all elements which do not contain themselves”. The existence of such an element is not a necessity for the existence of numbers.
2.7. A Fundamental Explanation of Quantum Mechanics
We have seen how unified entities represent the fundamental structure of our consciousness. Quantum mechanics is said to be fundamental so we will see how the concept of unified entities coincides with those properties of quantum mechanics that are truly fundamental.
The Schrödinger equation is the most fundamental equation in quantum mechanics, yet it is an equation which is based on Newton’s second law as any wave equation is. That means that classical mechanics is more fundamental than the Schrödinger equation itself. Then why is quantum mechanics considered to be fundamental? I believe that it is not the waves themselves which are fundamental. What make quantum mechanics considered as fundamental are concepts such as entanglement, the measurement problem and quantum events. I’ll refer to fundamental processes in a quantum measurement as a quantum event. Quantum events and entanglement are concepts which are closely related to each other. It is because entanglement defines an instantaneous relation between particles, such that quantum events depend on entanglement in order to maintain conservation of energy and momentum.
In quantum mechanics we see that fundamental concepts such as the quantum event and instantaneous relations occur on what seems to be a less fundamental level than what is described by classical mechanics. In other words, the quantum realm occurs not only on sub atomic levels and in relation to space, but occurs on molecular level as well. How could that be possible if we assume that the mentioned quantum concepts should be as fundamental as the smallest building blocks in physics? One way to explain it could be by assuming that unified entities are the most fundamental building blocks in physics and that they are a generalization of the instantaneous relations implied by the concept of entanglement. That implies that the property of instantaneous relation implied by the concept of entanglement is the same property from the definition of unified entities which would be the instantaneous relation due to confinement. Then we see how it is possible that fundamental properties of nature occur at molecular level and beyond molecular level, which is due to the property of containment. For example it could be that a unified entity confines unified entities related to molecules which again confine unified entities related to sub particles, which again confine areas of space and so on.
The theory of quantum decoherence explains that when one measures the particles quantum state, one of the quantum states will be related to the measurement instrument and the others to the environment ( Kiefer & Joos, 1998 ). What happened in that case is that some of the quantum states were disconnected from the particle, and related to the environment or the measurement instrument. What does it mean that quantum states become related to the measurement instrument or the environment? Most likely such “relations” is a result of the property of confinement. Then we see that a fundamental basic step of changes/action in the universe (the quantum event) seems to be that the contents of quantum states are connected and disconnected to other quantum states. So if our hypothetical generalizations are correct, a result of the quantum event is that the quantum states exit or enter confinements.
Where in our brain is our consciousness? We have observed the property of confinement to exist within our consciousness. As such it is possible that our consciousness exists as something confining many superpositions. In that case how spread out in space superpositions themselves can become do not determine the limit of the confinement by our consciousness. This may clarify the mystery of how consciousness can exist within the brain. While a single neuron cannot explain the property of thoughts, a collection of larger parts of the brain as e.g. an entanglement between more superpositions may contain enough information to explain a thought. In other words, our consciousness confines many superpositions within our brain, such that the collection of these superpositions contains more information than a single neuron and contains the information which we consciously experience. This process is not bound by locality, because the property of confinement itself contradicts locality.
2.8. The Most Basic Event
Changes constantly occur in the universe, because it is not constant. “The most basic event” must then be the most fundamental explanation of how the universe changes. From the previous chapter we discussed how consciousness and quantum mechanical concepts such as quantum events and entanglement coincide at an equally fundamental level from an objective point of view. Consciousness truly exists according to Descartes, and if we assume that it is fundamental in nature, it should be related to cause and effect or in other words “the most basic event”.
Evolution functions by the principle of natural selection. Natural selection lets those individuals with advantageous differences survive. Conscious experiences and their subjectively experienced values are only relevant to how our consciousness is aware of them or observes them. Consciously experiencing the positivity or negativity associated with thoughts cannot result in any physical difference, since the act alone of observing them as such has no objective relevance. Thus consciousness must be able to do something else than simply observing in order for subjective value experiences to have been selected by natural selection. That which consciousness can do which resulted in natural selection will be what we refer to as “the most basic event”.
In the following I will illustrate the argument in greater detail. The brain seems to carefully select what information should enter our consciousness, and that it is constructive and coherent. Why would the brain do that? Does it make any difference what information our consciousness is processing? If a consciousness can’t make any difference based on the information which it confines, then it would not matter what information is filtered into the consciousness, right? Evolution would not select the brain to give coherent and relevant information into the consciousness if it served no purpose that exactly this information is experienced by consciousness, while more irrelevant information is processed subconsciously.
Notice how positive and negative emotions are related to our thoughts. It seems as if our consciousness is rewarded with pleasure when eating, for a purpose. If we were passive observers (unable to perform “the most basic event”), being subjectively rewarded and punished by our emotions would serve no purpose which could not be accomplished by neutral experiences. If there would be something else instead of our consciousness which would be responsible for our choices, it wouldn’t depend on the subjective experience of pleasure or pain. So if we take into account that our emotions are selected by evolution in order to appeal to our consciousness for a purpose, consciousness itself must be able to cause a difference based on it.
If we somehow associated everything that was positive to be negative instead and everything that was negative to be positive instead, would that make any difference in our behavior? If the answer is yes, then subjective value perceptions definitely have a purpose. They have a purpose because our thoughts and how our thoughts are related to each other is carefully selected by evolution with the only purpose of being experienced by our consciousness. Since the concept of value only exists as an experience by our consciousness, then our consciousness is the only thing which can fulfill the purpose of value. Hence our consciousness must be able to perform “the most basic event”. In order to truly understand this, it might be necessary to subjectively realize the nature of the conscious experience of value, that it has a subjective meaning to us in terms of pleasure and pain.
I will summarize again. The relevance of value of our subjective experiences of pleasure and pain only exists in relation to our consciousness. Thus if there is a purpose behind experiencing value then our consciousness is the only possible thing which can fulfill this purpose, cause the experience of value exist in relation to nothing else. Thus our consciousness must be able to be a cause which results in an effect. Let us understand these arguments purely in terms of cause and effect:
Evolution → Brain → Conscious value experiences which only have subjective relevance (not objective relevance) are experienced by consciousness → Consciousness executes the most basic event because that is the only way to explain how the initial purpose of evolution is fulfilled.
So since the coherence or value of subjective experiences is only relevant to our consciousness, our consciousness performs the most basic event to fulfill the purpose of survival selected by evolution.
Now we need to make the final generalization to complete the model of unified entities, which is that all unified entities can perform the most basic event. According to the definition of unified entities and our generalizations between unified entities and quantum decoherence, it seems that the result of the most basic event is to change the structure of confinement between unified entities. Recall that the earlier generalization was that entanglement and unified entities are assumed to be the same. We also assumed that when the quantum states become related to the measurement instrument or the environment that this “relation” is due to confinement by unified entities. Also when different thoughts enter or exit our consciousness we can also say that they enter or exit confinement. Hence the assumption that the result of the most basic event is a change in the structure of confinement seems consistent with how we observe changes on the most fundamental level of reality.
It is difficult to identify how we as a consciousness perform the most basic event. We cannot be aware of it, since the act itself of causing a change is not information itself based on how we explain information in the following chapter. We notice it as change of information. Obviously not all the changes in our consciousness are caused by our own consciousness. Most of the time it is due to other unified entities.
2.9. A Fundamental Explanation of Information
It can be explained in terms of structures of confinements. For example, if the thoughts of an object and its name are confined, then it is information that they are the same. In other words it is information about the name of the object. Besides being confined, we can still distinguish between the object and its name because they are also confined from each other by other confinements. We see that this satisfies the property of symmetry as it is defined in physics and which I defined earlier as; observing a similarity while something else is different. The property of symmetry is satisfied if two thoughts are confined together by the same confinement (similarity), while the two thoughts themselves are different or distinguishable from each other. Symmetry is today considered a fundamental explanation of information.
There is also a type of symmetry in our consciousness which is not as directly caused by being contained by unified entities. That is when different thoughts consist of equal qualitative properties. Such as that two different objects can have the same “qualitative property” (e.g. same color). That these two different objects have the same color is not caused by those unified entities being related together by another unified entity, unlike the perception that outside and hot is the same. The structure of unified entities may also be information. An example of that could be conscious experience of observing equal shapes.
The philosopher David Hume mentioned that some objects are clear in our mind and some are not as clear. Perhaps how clear or thoughts are, may be proportional to the amount of unified entities within them. Our perception of sight is after all very clear, and seems to be rich in unified entities structuring our mental picture.
2.10. The Hard Problem of Consciousness
The philosopher David Chalmers presented what he refers to as the “hard problem of consciousness”. I will quote him as follows:
It is undeniable that some organisms are subjects of experience. But the question of how it is that these systems are subjects of experience is perplexing. Why is it that when our cognitive systems engage in visual and auditory information-processing, we have visual or auditory experience: the quality of deep blue, the sensation of middle C? How can we explain why there is something it is like to entertain a mental image, or to experience an emotion? It is widely agreed that experience arises from a physical basis, but we have no good explanation of why and how it so arises. Why should physical processing give rise to a rich inner life at all? It seems objectively unreasonable that it should, and yet it does ( Chalmers, 2010 ).
Is it possible to explain the very act of experiencing? It relates directly to existence and is thus fundamental. Recall the chapter called “the concept of fundamental”, where we can explain bottles in terms of molecules, but we cannot explain molecules in terms of bottles. We arrive at a similar dilemma while trying to explain the very act of experiencing.
However, we have seen how the property of confinement is as fundamental as our consciousness. Our consciousness and conscious experiences can be understood as structures of confinements. The property of confinement explains the origin of information, as explained in the previous chapter. Moreover we have seen how structures of confinements explain those concepts in quantum mechanics which can be considered fundamental. Thus the property of confinement is fundamental enough to provide new understanding of how consciousness and information arises from the brain.
The information which we perceive within our brains seems to be stored on a molecular level. Different molecules and their combinations is information. Fundamentally molecules are structured in terms of protons, neutrons and electrons. This fact alone does not explain the origin of information. Then the only relevant thing which varies between different molecule combinations is how they vary in terms of their structures of confinements, for example in terms of their molecular structures in terms superpositions and how molecules become subject to entanglement. This is something we can conclude based on how we generalized unified entities into quantum mechanics. The argument for such a generalization should be strengthened by how consistent modeling physics in terms of unified entities turns out to be with current models in physics. As such it seems that different qualia are determined by different structures of confinements.
Another argument could be that we can consciously experience the property of confinement, and thus a change in the structure of confinements alters our conscious experiences as well. For example if we imagine an elephant and then later a room, and then again unify these two perceptions into the perception that the elephant is in the room, this perception has then turned into something with a different qualitative property than the two original perceptions in themselves. Recall earlier discussion where it was concluded that even perceived positions within perceptions of sight implies structures of confinements. We can conclude that the qualitative properties change, based on how unified entities are connected. Can this be generalized to explain why we see colors? We have seen one way how qualitative properties of subjective experiences vary. Why would there need to be any other explanation for the case of different colors?
It seems that there is a limit to how many layers of containment which we can observe. Perhaps when the layer of confinement becomes too small or deep, perceptions of confinements become replaced with the perceptions of sensations such as for example colors. Fundamentally the subjective sensation of different colors is caused by the very act of experience. As discussed the act of experience is also related to confinement, since we only experience those thoughts which our consciousness confines. Since our brain determines our thoughts by storing information on a molecular level, different colors have to be determined by structures of confinements.
Why do we experience time as slow compared to how fast changes occur at for example particle level? As we know, any change has to be the cause of the most basic event. Perhaps before our own consciousness performs the most basic event, it needs to experience enough internal change to reach a point of motivation. Individual unified entities that are of deeper layer of containment may need to perform an amount of most basic events before our consciousness reaches point of motivation to perform the most basic event itself. Therefore unified entities which are in relatively deeper layers of containment execute the most basic event at a higher rate. They need to make an amount of internal change, before the unified entities confining them can cause the most basic event. This could be why we experience time as slow compared to the enormous rate of displacements more directly related to planch length for example.
3. Modeling Physics as Structures of Confinements
Physics objectively exist, and according to Descartes, our consciousness exists as well. At some point physics and consciousness must even relate to each other. Perhaps it is reasonable to assume that they exist in a similar way? The approach to model physics in this article will have foundation based on generalizing existing fundamental properties of consciousness. We have determined that unified entities represent a truly existing property within our consciousness, which is the property of confinement. This property is fundamental because we can identify it as a general property of any of our subjective thoughts. Moreover we have seen the similarities unified entities have with those properties of quantum mechanics that are truly fundamental. With fundamental understanding, we can generalize. Just like we generalize molecules to explain materials, we can generalize unified entities to explain physics. By generalizing we can obtain new information and obtain a deeper understanding of physics.
The following models will be hypothetical investigations of how physics may arise from properties of consciousness. I will present two different models based on unified entities. One of the models will be explained in the chapter called “Introducing some of the potential of the mathematical model”. The other model will be introduced in the chapter called “foundational layers of confinement”. The latter model will be different and more detailed. Despite the differences of these two models, both of them imply basic laws of physics including relativity. These implications seem to be a natural result of the definition of the model itself. Due to the amount of details in physics which we will be able to model in terms of unified entities, it seems likely that by the logic of induction that further details in physics can be modeled in terms of unified entities.
3.1. The Mathematical Model of Unified Entities
A mathematical model of unified entities is shown in Figure 1. The purpose of this model is to visualize the
Figure 1. The figure shows different unified entities and how we may model the result of the most basic event.
properties and structure of unified entities, and to show how the most basic event can possibly occur. Unified entities are represented as circles confining other circles. The property of unified entities is that they can:
1) Contain other unified entities.
2) Perform the most basic event by changing the structure of confinements.
By investigating quantum decoherence combined with the assumption that unified entities and entanglement is the same concept, we concluded that the most basic event results in a change in the structure of how unified entities are confined. A possible result of a most basic event can be seen in Figure 1 as the difference between the left and right side of the arrow. In this case the outermost unified entity caused the most basic event. It could not be for example the unified entity labeled “2”, because it cannot change the structure of unified entities which it does not contain. Also the most basic event depends on structure of confinements since different structures of confinements imply different information.
Even if the most basic event must result in a change in structure of confinement, we do not know exactly how this occurs. There are concepts such as for example positivity, negativity and information which determine the most basic event. We do not fully understand how these concepts relate to the most basic event, or how positivity and negativity relates to structures of confinement. Perhaps lack of symmetry within the structures of unified entities (lack of information) or chaos could result in the sensation of negativity. It is because I can personally and generally relate negativity to the unknown. The question would then be whether evolution caused this fact or discovered this fact. Similarly positivity is often associated with the feeling that things are known and within control.
3.2. Introducing Some of the Potential of the Mathematical Model
In this chapter, I will present the first of the two mentioned models in physics. This one will be an introductory example of how unified entities may predict physics. It already seems to lie in the definition of the model of unified entities to be consistent with those properties of physics which may seem mysterious. Unified entities are per definition non-local which in itself demystifies the non-locality in quantum mechanics. We will now see how unified entities can easily unify the properties of mass, momentum, time and relativity in a simple analogy representing a one dimensional case. This is an example of how the property of confinement and the most basic event imply fundamental properties in physics.
Consider Figure 2. We will consider an analogy to the properties of unified entities. Imagine that the black circles are barrels. The red or green circles within some of them are red and green marbles. Then imagine that every minute a person will pick a random marble. If the person picks a red marble, he will take all of the marbles and move them to the next barrel to the right. If the person picks a green marble, nothing happens. He will just leave the marbles there until a red marble is picked at a later time. You can imagine that there are an infinite amount of barrels continuing to the right outside of the drawing.
The result of these set of rules which I just gave is that the marbles with red ones among them will be slowly displaced over time in the direction to the right. The group of only green marbles will be standing still forever. We see that the more red marbles there are, the faster the marbles travel. If the red marbles represent momentum and the green ones mass, then it follows that when we have more momentum, the particle travels faster.
If there are a lot more green marbles than red ones, the red and green marbles become inversely proportional
Figure 2. Analogy in terms of barrels and marbles which illustrates the relationship between mass and momentum. The green marbles represent mass and the red marbles represent momentum.
to each other in relation to how they predict velocity. The formula for momentum indicates that mass and mo- mentum are inversely proportional to each other. So then the green marbles would be proportional to mass and the red ones proportional to velocity. Comparable to the assumption that there are a lot more green marbles than red marbles, the formula for momentum only applies to objects with a velocity which is much more close to standing still than the velocity of light.
Assume from now that the rules change a bit such that every minute when the person picks any marble, he will move the marbles to the next barrel, regardless of whether the marble is red or green. What is the result then? It is that the marbles will travel at the same max velocity regardless of how many marbles are within the group.
Let us translate this analogy to the properties of unified entities. The circles represent confinements. The most basic event occurs at a steady rate and is in the analogy represented by that a person chooses a marble each minute. The green marbles represent mass. When the most basic event relates to mass, the system remains in its current position. The red marbles represent momentum and when the most basic event relates to momentum, the whole group of marbles is displaced to the next position. If another unified entity which is not illustrated in Figure 2 would happen to confine the marbles, they could all be displaced in a single most basic event, if the unified entity confining the marbles was to be displaced to adjacent “barrels”.
In relativity we know that as velocity increases to a comparable velocity of light, the system gains more mass. Let us see how this can become a natural consequence of this same analogy except that we now introduce the perspective of relative velocities. Let us look at Figure 4. It is kind of similar to Figure 3 except that the blue marbles are gone. The upper barrel with marbles still contains 3 more red marbles than the one below. This means that there will be relative motion between the marbles in the upper barrels and the marbles in the barrels below. The question is which relative motion is faster? Is it the one from Figure 3 or from Figure 4? It is the relative motion in Figure 4 which is faster, because the red marbles will be displaced often compared to the few other green ones. In Figure 3 the red marbles will be picked so rarely, that the relative motion will be very slow.
Now for a similar reason that the relative motion in Figure 3 is slower than in Figure 4, could be why relative motion within a rocket at relativistic velocity is slower. If all relative motion is slower, it follows that perceived time, and length is slower as well. The analogy between the figure and physics is as follows. The green marbles represent mass, the blue marbles represent momentum and the red marbles represent momentum as well. However, the blue marbles gain the property of mass, when evaluating only the motion due to the red marbles. What is the difference between the red and the blue marbles then? It is simply that the red and blue marbles represent motions which are relative to each other.
The inverse proportionality between marbles representing mass and marbles representing momentum remains true according to the mechanism in Figure 4, for slow relative motion. Since the blue marbles gain the property of mass, there are few red marbles compared to the total marbles representing mass. When there are many enough marbles representing mass compared to marbles representing relative motion, inverse proportionality is the case. When the blue marbles gain the property of mass, it shows how momentum and mass increases when velocity increases. When mass increases time decreases. Length contraction occurs because length is a function of time.
Figure 3. Analogy in terms of barrels and marbles which illustrates relativistic effects of relative motion. The green marbles represent mass, the blue marbles represent momentum for non-relative motion and the red marbles represent momentum for relative motion.
Figure 4. Analogy in terms of barrels and marbles which illustrates how lower velocities results in less relativistic effects. The green marbles represent mass and the red marbles represent momentum.
3.3. Time Is Relatively Slower in Both Frame of References?
What I’ve always found to be intriguing about relativity is how two frames of references both predict that the time is slower in the other frame of reference. In the models based on unified entities presented in this article, only one frame of reference can truly be slower than another relative to space. That is not a problem, so I will clarify how it is fundamental that one frame of reference can predict that the other is slower, even if it isn’t really slower.
Let us assume in this thought experiment that there is only one frame of reference which is standing still relative to space. Then imagine two frames of references; Earth which is standing still and a rocket which is moving at a relativistic velocity. Then time will be truly slower in the rocket than on Earth. The person within the rocket will falsely measure that time is slower on Earth than in the rocket. Is this possible?
First we will see how a person on Earth would measure time within the rocket. Then we will analyze what happens when a person within the rocket performs the same procedure of the measurement to measure time on Earth. We evaluate both of these measurements in Earth’s frame of reference. Earth’s frame of reference would in this thought experiment be the “true” one, or the one which is standing still relative to space.
If the person on Earth wants to measure that time is slower in the rocket, he needs to do as follows. First he measures the time interval, t on Earth. At the beginning of this time interval we assume that the rocket is right above Earth traveling at velocity, v, and that he observes light signals showing the time from the clock inside the rocket. After time, t, the rocket has traveled a distance of v∙t, so now the light signals showing what is the time
on the rocket clock needs to travel for a time, 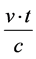 , before it can be read back on Earth again. Hence the person on Earth must wait
, before it can be read back on Earth again. Hence the person on Earth must wait 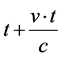 seconds between two clock readings of the clock in the rocket, to see how much time has passed within the rocket during the time interval, t, on Earth.
seconds between two clock readings of the clock in the rocket, to see how much time has passed within the rocket during the time interval, t, on Earth.
If a person within the rocket does the same measurement still considered from Earth’s frame of reference, the person within the rocket travels further than he is aware of when he waits the time  according to his
according to his
clock. That is because when time is slower for him, he will travel for a longer time and will reach a further distance in space. This means that the light which he sees has traveled a much longer distance too to catch up and thus the light will be much older, showing an earlier time. As such the person within the rocket predicts an older time at Earth, making him conclude that time on Earth is slower than it is. But it is truly a direct result of that it is his time within the rocket which is slower. If you make the calculations, the person in the rocket predicts that time on Earth is just as much slower as the person on Earth predicts that the time within the rocket is slower. For example if the person on Earth thinks that time is half as slow within the rocket, the person within the rocket will think that time is half as slow on Earth. In other words the light from a clock on Earth that catches up to the
rocket after waiting the time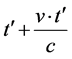 , shows an early clock reading such that it looks like time is as much slower on Earth as the time dilation formula corresponding to v would predict.
, shows an early clock reading such that it looks like time is as much slower on Earth as the time dilation formula corresponding to v would predict.
It is important to note that the person within the rocket does not measure time on Earth to be slower because there are relativistic effects on Earth. He only predicts time to be slower on Earth because his own frame of reference has slower time. This is why the following models in terms of unified entities which accommodate only one inertial frame of reference remains consistent with relativity.
It is known that each frame of reference predicts that each other are slower. I’ll refer to this fact as that they are making symmetric predictions. We can assume that there is a very fundamental reason for why this symmetric prediction occurs. Going back to our example of Earth and the rocket, it follows from the Lorentz factor that by making predictions based only on Earth’s frame of reference, that a person on Earth predicts that a person in the rocket predicts that Earth is slower. This mathematical prediction occurs when the person in the rocket is assumed to be in a frame of reference which is truly slower than Earth’s frame of reference. This prediction of a frame of reference with such a different property which is that only one of the frame of references is the inertial one is a necessary element in order to explain the consistency of symmetric predictions, since without it we see that the person on Earth would not know how the person in the rocket predicts the symmetric prediction. Thus the prediction of an inertial frame of reference is more fundamental than the fact that they make the symmetric prediction. Why do such predictions of inertial frame of references emerge when we try to understand why the symmetric prediction occurs?
3.4. Directional Symmetry
Before we model physics in more than one dimension, we need to understand what I will refer to as directional symmetry. Why is Pythagoras Theorem the relation which describes vector addition? Why isn’t it the case that we describe vector addition as the sum of their lengths? This is easiest to explain by the help of illustrations:
Let’s say that the length of each red vector in Figure 5 is 1. Then the length of the green vector is given by the vector sum:
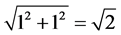
The vector sum of the two green vectors in Figure 6 is given by:
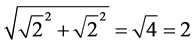
What is interesting to notice is that the result of the vector addition of the green vectors equals the sum of the decomposed red vectors. Let us now assume that vector addition occurred by summing the whole length of each vector instead of following the Pythagorean Theorem. The vector sum of the green vectors would then be 2 + 2 = 4. This would not anymore give the same result as summing the decomposed red vectors.
This means that if vector addition occurred by summing the lengths of the vectors, we could increase or decrease the speed and calculated energy of objects only by changing their direction of motion. Let us refer to the fact that vector addition follows Pythagoras law in any direction as directional symmetry.
A model accommodates vector addition if motion occurs equally fast in any direction. Figure 7 illustrates
Figure 5. The green vector represents the velocity of an object and the red vectors are the decomposition of the green vector.
Figure 6. The figure to the left shows two green vectors, representing two velocity components of an object, and the red vectors is the decomposition of the green vectors. The figure to the right shows the result of summing the green vectors.
Figure 7. A model of two two-dimensional space which is consistent with vector addition for motions occurring in any direction.
how this property can be maintained. We assume that Figure 7 represents only a tiny part of a larger structure and that the circles intersect randomly with no directional bias, to nearby circles. The confinement of each circle defines a position. Position may be changed from one circle to another, only if the circles intersect, such that the property of length is maintained. The property of length is that before one may reach one position, one has to travel through those in between, if there are any. After traveling through one million circles, in any particular direction, one would travel equally far, which means that the model accommodates vector addition in any direction. It is the randomness of how the circles relate to each other which results in directional symmetry, or in other words that vector addition is accommodated in any direction.
3.5. Foundational Layers of Confinement
From Figure 7, it seems that when unified entities relate to each other in what seems to be arbitrary ways, that they satisfy directional symmetry, and thus vector addition. Figure 8 can be considered a more detailed version of Figure 7 and models two dimensional space. Still we can assume that it is only a simplified version of even more realistic models in terms of confinement. A more realistic model could for example contain more layers of unified entities and, have different amounts of unified entities within their confinements and be generalized to accommodate three dimensions. However, by studying Figure 8, we may already see how the laws of physics may naturally fall into place.
In Figure 8, we can see different layers of confinement. The colored squares are the outermost confinements in the illustration. They confine the black circles. The black circles confine the brown confinements. Let us refer to the layer represented by colored squares as d-entities. The black circles are referred to as p-entities and the brown confinements are referred to as s-entities.
We can see that d-entities relate to each other because that they sometimes confine the same p-entities. This causes d-entities to have relative positions to other d-entities. We can assume that Figure 8 continues with the same logic in terms of layers and confinements outside of its drawing. If we look at Figure 7, d-entities would correspond to the black circles. Then by comparing Figure 7 with Figure 8, we see that the black circles in Figure 7 can possibly relate to each other by confining common unified entities where they intersect.
In general d-entities displace s-entities between p-entities. If an s-entity is displaced to a p-entity which is also within the confinement of new d-entities, it can possibly be displaced to other p-entities which it previously could not. As such it can travel to p-entities which are confined by d-entities that are far away. This results in the property of length and displacement in physics. The most basic event executed by d-entities occurs at a limited rate, but in an average constant rate, which possibly results in the concept of time as it is defined in physics. This limitation is the source of a maximum amount of displacements and defines the limitation in how fast s-entities can travel. It is the reason why the speed of light is the maximum velocity.
3.6. A Fundamental Model of Classical Mechanics and Relativity
Based on the model from Figure 8 we can assume that a particle is a structure of confinements which to some local extent confine certain s-entities. Those s-entities are then displaced by d-entities at an average rate. Since the particle confines these s-entities, it may follow them or the majority of them wherever they are displaced. If
Figure 8. The figure illustrates how unified entities can relate to each other in order to accommodate the properties of two-dimensional space, maintain consistency with vector addition in any direction and define motion.
s-entities within the confinement of the particle are constantly displaced in a certain direction, the particle as a whole will also move in that direction. We will discuss what determines directions of motion in the next chapter.
A single d-entity is responsible for displacing the particle in any direction. If the particle moves for example 5 times in the x direction, but in the meantime moves 3 times in the +y direction and another 3 times in the ?y direction, the particle will spend longer time to reach destinations along the x-axis. This basically results in the property of mass, since mass slows down particles.
When we observe the movement of a macroscopic object, we know that it consists of particles. These particles have a large amount of inner motion which we do not see and which is not in the same direction as the motion which we observe on a macroscopic level. We know of the mentioned inner motions due to being caused by inner forces of the particles such as orbiting electrons etc. Since these motions occur in more than one direction, they will slow down the motion in the observed direction of motion according the current model. We can conclude that based on the discussion in the previous paragraph. The property of mass is to give particles the opportunity to move at velocities which are less than the max speed of light, and thus mass slows down particles. The current model in general predicts the concept of mass in terms of the mentioned unobservable motions such as orbiting electrons and so on.
Newer research, Gauthier (2015) , suggests that an electron is a spin ½ charged photon moving in a helical path. We see that in addition to moving in the observed direction of motion, it has a circular component. Since it is a photon it moves at the speed of light. However, this circular component causes it to move a longer path than what we observe. Gauthier concludes that the radius of this circular motion determines the velocity of the particle, such that a larger radius implies lower velocity. Increasing the velocity can also be considered a vector rotation, such that the electron changes direction of motion to move more towards the forward motion component of the helical path than the circular. This seems consistent with how the current model in terms of unified entities predicts mass, if we generalize the properties of Figure 8 to accommodate three dimensions. This is possible by assuming that there are more d-entities which confine common p-entities with other d-entities.
Figure 9 shows the light paths from Einstein’s thought experiment from which the Lorentz factor is derived. The triangle shows a vector addition. Let us consider two frames of references. Frame of reference with zero velocity has an observer in it referred to as observer A. The frame of reference with velocity, v, has observer in it referred to as observer B. Observer A observes motion v*t and A, but not side B. Then side B is non-observable motion and thus motion due to the property of mass. Observer A concludes that motion due to traveling the length v*t is observable motion, and thus forward motion in his frame of reference. However, observer A knows that observer B considers motion due to traveling length v*t as unobservable motion, which is why observer A predicts that this unobservable motion has the property of mass such that it slows down the time for observer B. It turns out that a more general definition of the property of mass is as unobservable motion. We concluded that observer A concludes that motion v*t has the property of mass, in frame of reference B, simply because this motion is unobservable or indeterminable within frame of reference B.
In the limit where the velocity is far from the speed of light, the Lorentz factor predicts classical mechanics. Then the question is how the current model is consistent with the Lorentz factor. Increasing the velocity v becomes a vector rotation of side A towards side v*t such that side B becomes smaller. This is similar to how Gauthier predicts the relationship between mass and velocity. Such a vector rotation remains consistent with the current model in terms of unified entities. We will discuss further details related to this in the following chapters.
Figure 9. The figure illustrates the frame of reference dependent observed lengths of light paths in Einstein’s thought experiment used to derive time dilation.
3.7. Ideas Explaining Charge
In the standard model in particle physics, fundamental particles are classified according to their mass, charge and spin. In the case of the charged photon model of the electron, Gauthier (2015) suggests that mass and spin may be the result of the helical motion. This is how the current model in terms of unified entities would account for mass and spin in general. What about charge? How can the concept of charge fit into the current model of unified entities?
Charge seems to relate to directions of motion. Equal charges repel each other and opposite charges attract each other. In order to understand why one direction of motion occurs instead of another, it must ultimately depend on the most basic event. The most basic event depends on information. An understanding of charge must incorporate information. Imagine a unified entity in a higher level of confinement than d-entities. Let us refer to such a unified entity as c-entity. If a c-entity confines for example s-entities in a line across several d-entities, then the c-entity confines information about this line which determines two possible directions along the line. Then the information relating to the difference of a positive or negative charge could decide which of the two directions the c-entity travels. The most basic event does not only depend on information. Perhaps it depends on some kind of value perception as well, such as positivity and negativity. Then such information about positivity or negativity could be a property within the mentioned line of s-entities. These properties could be maintained by higher levels of confinement as a characteristic structure of confinements within the s-entities in the line. We may need to learn more about such value perceptions and how it relates to the most basic event to come up with sufficiently detailed models of charge and how it relates to direction of motion.
Let us assume that a charge is a unified entity which confines larger areas of space. They can possibly emit c-entities traveling in random directions. These c-entities together constitute the electric field around the charge. Let us denote c-entities which are emitted from a positive charge as cp-entities, and c-entities which are emitted from a negative charge as cn-entities. When a charge travels near c-entities they accelerate. We assume that the charge absorbs c-entities such that they confine them. This absorption occurs as follows. The charge confines a very large area of space. There are unified entities within the charge causing absorption of c-entities to the charge by the most basic event and this occurs from each p-entity which the charge confines. Thus absorption of c-entities depends not on frame of reference but on the density of c-entities. If a positive charge absorbs cp-entities, it accelerates in the same direction as the cp-entities. If a positive charge absorbs cn-entities, it accelerates in the opposite direction which the cn-entities travel. For a negative charge the opposite is the case.
How do c-entities contribute to the acceleration of a charge? Perhaps it could be similar to how marbles of different colors compete with each other in the introductory example illustrated in Figures 2-4. Then c-entities causing relative motion or motion in different directions are comparable to marbles of different colors. When there are few c-entities representing relative motion, it is like Figure 3, where there are few red marbles compared to the rest. If there are many c-entities causing unobservable motion such as the circular component in the helical motion which is mass, compared to c-entities causing observable motion such as the straight forward motion which we can observe in objects, then classical physics and inverse proportionality applies. The inverse proportionality is then between c-entities representing observable and unobservable motion. It is similar to how motion due to red marbles would be inverse proportional to the green marbles in Figure 2, if there were a huge amount of green marbles compared to red ones. This implies that c-entities are proportional to velocity in the direction which they are contributing in the limit where these velocities are far from the speed of light. However, why does the Lorentz factor apply and not inverse proportionality? It is because we assume that the most fundamental particles move in helical paths. This path is longer than the observed path of motion. The helical path and observed path of motion mathematically relate to each other similar to how side v*t and side A relate to each other in Figure 9. It is because the true direction of motion of the particle is not in the observable path of motion, but in a helical path which is a rotating vector with constant non-zero angle relative to the observed direction of motion. We understand the motion of a particle in a helical path as such that it has a rotating vector component. Then moving along the forward component of this helical path with a constant angle relative to this direction implies that velocity relates to mass similar to how side v*t relates to side B in Figure 9. This is how the current model is consistent with the Lorentz factor. In order to completely outcompete the c-entities responsible for mass, and accelerate the particle to the max velocity, an infinite amount of c-entities contributing to forward motion would be required. Similarly relativity predicts that an infinite amount of momentum is required to accelerate a particle to the speed of light. In this case side A and thus side v*t would become infinitely long and side B infinitely small. This would all be caused by that side A gains an infinite amount of c-entities compared to side B.
What is the exact mechanism causing c-entities to decide the direction of motion of the charge? Further knowledge of the most basic event may be required to answer this question with more certainty. There could be a line or at least two points which determine the direction of motion. Each c-entity could then contribute to changing the direction of these two points in a way which is consistent with the previous paragraph. Another way could perhaps be to assume that each c-entity is confined and still in motion, but the charge just follows or in other words remain confined to the majority of them, or a random amount of them. Maybe there are other more complicated ways depending on information, higher levels of confinement and the most basic event even in ways that the current model does not sufficiently predict yet. It could also be that the foundational levels of confinements modeled in Figure 8, need to be reconsidered to determine another structure of space to predict further details in physics, or that further layers of confinement would have to be added.
The formula for the electric field around a point charge, predicts the density of c-entities. The density of c-entities is proportional to the electric field strength. The c-entities do not occupy space in a way which resembles how electric field lines are drawn. It is only when a charge itself travels near c-entities that it accelerates according to how the electric field lines are drawn. This occurs due to how the densities of c-entities vary. The densities dissipate away from the charge because the amount of d-entities which c-entities can travel to increase when they travel away from the charge. Since our model of space is directionally symmetric, the density of c-entities will decrease at a similar rate as the formula for the point charge would predict how the electric field decreases. The formula for a point charge predicts that electric fields on top of each other are the sum of the field of each charge. This addition implies that the density of c-entities are unaffected by other nearby c-entities.
3.8. A Fundamental Model of Newton’s Laws of Physics
Is how we modeled charge and electric fields consistent with Newton’s laws of physics? Newton’s first law says that once a charge is accelerated it maintains its motion for all eternity until accelerated again. According to how we modeled charge, only c-entities and thus acceleration can change its current state of motion. Thus the model is consistent with Newton’s first law.
Newton’s second law predicts that how much an amount of mass accelerates is a measure of force. Earlier we hypothesized how direction of motion changes when a charge absorbs c-entities. In helical motion, there is a circular and forward component. Accelerating the particle would be equivalent to changing the proportion between the circular and forward component of the helical motion. We interpreted the proportion between the circular component and forward component as a proportion between different c-entities. In the limit where the velocity is measured as far from the speed of light, inverse proportionality between mass and velocity applies. Then each c-entity has an approximately equal contribution to acceleration which implies consistency with Newton’s second law.
Newton’s third law states that for every force there is an opposing equal force. Let us assume that fundamentally each smallest particle or unified entity with the property of charge has an equal charge. If they have equal strength in charge, they produce the same field and will obviously experience an equal force. Let us look at an example to see how the current model is consistent with Newton’s third law. We will refer to a positively charged particle and a neutral one which are binded together by e.g. the strong force as group 1. Then we will refer to another equally positively charged particle which is relatively far away as group 2. We further assume that the neutral particle has the same mass as the two positively charged particles in this example. The positively charged particles will produce an equal electric field and thus emit an equal amount of c-entities towards each other. However, due to having more mass group 1 will accelerate slower. In group 1 the positively charged particle accelerates and will then transfer c-entities to the neutral one through their own binding, such that the neutral particle obtains the same acceleration. This means that while group 1 obtains the same amount of c-entities in total, it is used to accelerate twice as much mass, and thus accelerate twice as slow as group 2. This means that the force exerted between group 1 and group 2 is the same.
How does the current model account for conservation of energy? Perhaps conservation of energy only occurs as a result of the equality between kinetic and potential energy. Any kinetic energy is the result of potential energy during particle interaction. Thus the kinetic energy will always be the same before and after particle interaction.
3.9. Higher Levels of Confinement
What about unified entities which confine d-entities and so on which we do not see in Figure 8? If there are unified entities which confine d-entities, they are in a higher level of confinement than d-entities. As such we can imagine an increasing hierarchy in layers of confinements. This could explain the non-locality which we observe in quantum mechanics. In lower levels of confinement, d-entities are responsible for displacing s-entities limited to possibly being displaced to adjacent d-entities for each most basic event. In higher levels of confinement, it must be the case that unified entities could displace entire particles beyond the scope of single d-entities. As such non local events are a natural consequence of the definition of unified entities.
Concepts such as entanglement and consciousness are in higher levels of confinement. Our consciousness follows the movement of particles, but not space itself. It could be because consciousness confines particles without confining space. Another explanation could be that consciousness confines both space and particles, but only follows particles, due to statistical reasons, or reasons related to the most basic event which we do not know enough about. In that case we do not observe space itself, because it is in a too deep layer of confinement. What confines our consciousness? If something confines our consciousness, does information appear to us similarly as it appears to unified entities in even higher levels of confinement?
3.10. A Solution to the Measurement Problem in Quantum Mechanics
The measurement problem is how quantum measurements are unpredictable. Quantum mechanics can only predict the outcome of a measurement with a certain probability. However, a probability indicates randomness. Is this randomness fundamental, or is there a more fundamental explanation for why quantum waves are limited to only give us information about the probability?
A solution to the measurement problem follows from generalizing the concept of entanglement. Previously we have discussed how unified entities and entanglement describe the same objectively. Unified entities are in that case the generalized version of entanglement. The fact that unified entities can confine other unified entities implies non-locality per definition.
The concept of entanglement is not predicted by the Schrödinger equation itself. It is observed and then it is accepted and generalized into the theory of quantum mechanics. This is yet another reason why it can be logical to generalize it even further and assume that entanglement can be more than just related to waves and quantum phenomena, and to something such as unified entities which represent basic properties of consciousness. The very nature of unified entities and the most basic event solves the problem of the principle of locality. Let us investigate an example of how unified entities could possibly explain the relevant properties of the wave function in relation to a quantum measurement.
A wave function in position space, describes the probability of measuring a certain position. This probability is indicated by the height of the wave function in a coordinate system, where the x-axis represents the position and the y-axis is proportional to the probability ( Griffiths, 2004 ). What quantity could represent such a probability? I think that it has to represent an amount of unified entities. If a quantum event relates to “the most basic event”, unified entities are the only quantity that can be the cause of it. From now on I will refer to unified entities constituting the height of a wave function as h-entities.
The result of a quantum measurement is that one of the quantum states constituting the wave function becomes related to the measurement instrument. According to the model of unified entities this must be caused by the most basic event. There may be unified entities confining the environment, the wave function and the measurement instrument. For simplicity, let us assume that there is one such unified entity responsible for confining these systems. We refer to it as an mp-entity.
The question is why is the wave function’s height proportional to the probability of the corresponding position being measured? The mp-entity causes one of the positions to be measured by executing the most basic event. In Figure 10, we see that it is modeled as such that a wave function contains b-entities (blue rectangles) which contain h-entities (black circles). The b-entities are those unified entities which relate h-entities to a particular position due to confining the h-entities. They could be the quantum states which the wave function is in a superposition of. In that case b-entities would be smaller waves, and slightly more spread in space than they appear in the drawing. Now, what if the mp-entity chooses which b-entity will be measured, based on any random h-entity? Then the b-entity which confines the responsible h-entity will be measured. The result is a uniform distribution among h-entities, causing those b-entities with more h-entities to be measured with a larger
Figure 10. The figure illustrates how unified entities can model the measurement problem. The black circles represent h- entities, the blue rectangles represent b-entities, the red circle represents a unified entity which is part of the measurement instrument and the green unified entity represents the mp-entity.
probability. So this means that the b-entities which relate to positions, are chosen with a probability proportional to its height as is the mentioned property of a wave function.
There are probably many ways to explain how unified entities can explain the measurement problem. Such an explanation would be reliable if it explains why the choice of b-entities relies on a uniform distribution of all the h-entities in the wave function, such that if one h-entity is picked, the b-entity containing that h-entity will be related to and measured by the measurement instrument.
If we consider how our own consciousness relates to the brain, it can be quite similar to the example above. Similar to that an mp-entity will choose a b-entity based on h-entities. Our consciousness needs to choose which part of the brain that processing of information should be increased. Let us say that we would be looking for a particular pattern in our sense perception of sight. Then we identify a mental object (which is a unified entity) containing this pattern and “choose” this object. Obviously an object with more sense perception within it will have a larger probability to contain the desired pattern than an object with less sense perception in it. As concluded much earlier, sense perception is constituted by unified entities. After choosing the mental object (comparable to b-entity) with the desired pattern (comparable to h-entities) the most basic event could occur by displacing this object. The most basic event in quantum mechanics and in our consciousness is after all the same concept.
4. Conclusion
Unified entities are based on the property of confinement which is determined to be a fundamental and existing property within our consciousness. Fundamental concepts are reasonable to generalize. It turns out that problems such as the hard problem of consciousness, how information exists, how numbers exist and how consciousness relates to the brain can be further understood in terms of structures of confinements. The most basic event is implied by analyzing consciousness, subjective value experiences, evolution and the brain. If consciousness is fundamental, it should directly relate to cause and effect.
It cannot be denied that the laws of physics seem to mathematically arise from basic properties of consciousness. We investigated two different models of physics in terms of unified entities. Both of them predicted how classical physics and relativity related to each other. The more detailed model predicted vector addition, classical physics, relativity, charge and Newton’s laws of physics. Non-locality and a solution to the measurement problem in quantum mechanics are implied by the definition of unified entities. Considering the fact that both of the different models predict properties in physics and the amount of details in physics predicted, the logic of induction strengthens an argument for that more properties related to physics can be modeled in terms of unified entities.
Cite this paper
NikolaiLyng, (2016) Structures of Confinements as an Empirical Property of Consciousness and a Fundamental Property in Physics. Open Journal of Philosophy,06,120-139. doi: 10.4236/ojpp.2016.61012
References
- 1. Chalmers, D. (2010). Ch. 2: Facing up to the Problem of Consciousness. Oxford: Oxford University Press. http://dx.doi.org/10.1093/acprof:oso/9780195311105.003.0001
- 2. Gauthier, R. (2015). Electrons Are Spin ? Charged Photons Generating the de Broglie Wavelength. SPIE9570, The Nature of Light.�
- 3. Griffiths, D. J. (2004). Introduction to Quantum Mechanics (2nd ed.). New York: Pearson Education International.
- 4. Kiefer, C., & Joos, E. (1998). Decoherence: Concepts and Examples. Universitat Freiburg: Fakultat für Physik.











