Received 10 November 2015; accepted 26 December 2015; published 29 December 2015

ABSTRACT

This paper proposes a decomposition of the cost of risk (as measured by a risk premium) across intervals/quantiles of the payoff distribution. The analysis is based on general smooth risk preferences. While this includes the expected utility model as a special case, the investigation is done under a broad class of non-expected utility models. We decompose the risk premium into additive components across quantiles. Defining downside risk as the risk associated with a lower quantile, this provides a basis to evaluate the cost of exposure to downside risk. We derive a local measure of the cost of risk associated with each quantile. It establishes linkages between the cost of risk, risk preferences and the distribution of risky prospects across quantiles (as measured by quantile variance and skewness). The analysis gives new and useful information on how risk aversion, exposure to downside risk and departures from the expected utility model interact as they affect the risk premium.

Keywords:

Risk, Quantile, Variance, Skewness, Downside Risk

1. Introduction

For risk-averse decision makers, the cost of risk can be measured by the risk premium reflecting the willingness-to-pay to replace a risky outcome by its mean. In general, the cost of risk depends on the nature of risk exposure. Special attention has also focused on the role played by downside risk, i.e. the risk associated with unfavorable events. Previous research has examined safety first models (e.g., [1] ), concerns with exposure to losses (e.g., [2] ), disappointments (e.g., [3] [4] ), below-target returns (e.g., [5] ) and catastrophic events located in the lower tail of the payoff distribution(e.g., [6] ). Much progress has been made characterizing aversion to downside risk (e.g., [7] -[15] ). Building on Arrow and Pratt’s seminal contributions ( [16] [17] ), the measurement of risk aversion “in the small” has been extended to apply to downside risk, generating local measures of intensity of downside risk aversion applied to small risks (e.g., [10] [12] [14] [15] )¹. But the strong linkages established by Pratt between risk aversion “in the small” and “in the large” have proved more difficult to extend to downside risk. For example, Keenan and Snow ([14] , p. 1097 and 1101) showed that no single local measure can provide a global characterization of downside risk aversion.

The complexities associated with a global analysis of aversion to downside risk suggest a need to explore a different approach. Like Pratt [16] , Arrow [17] and others, it is natural to start with the risk premium as a measurement of the cost of risk. But while Arrow and Pratt examined the linkages between the risk premium and risk exposure “around the mean”, such an approach appears less fruitful when focusing on risk located in the lower tail of the payoff distribution². This paper examines the cost of risk (as measured by the risk premium) using a quantile approach. This is done by dividing the range of stochastic payoff into intervals, each interval characterizing a quantile of the underlying distribution. This allows us to examine the nature and welfare effect of risk exposure in each interval/quantile. We first show that the risk premium can be decomposed into additive components across quantiles. This result is global and applies “in the large”. It provides a direct measure of the cost of exposure to downside risk. Indeed, defining downside risk as the risk located in the lower quantile(s) of the payoff distribution, the cost of downside risk is just the component of the risk premium associated with such quantile(s). We also show our global decomposition can generate local measures that apply “in the small”. In turn, these local measures provide some useful information about linkages between risk preferences and moment-based measures of risk exposure.

We present our arguments under general risk preferences represented by a general smooth preference functional over the probability distribution function of payoff. While most previous research on downside risk aversion has focused on the expected utility model (e.g., [8] [10] [12] [14] [15] ), this seems unsatisfactory for three reasons. First, the expected utility model assumes that risk preferences are “linear in the probabilities”; but there is strong evidence that this provides an inaccurate representation of risk preferences (e.g., [2] [18] -[20] ). Second, prospect theory has documented that individuals tend to “overweight” the probability of rare events [2] . This is relevant in the evaluation of downside risk when these rare events are located in the lower tail of the distribution (e.g., the case of catastrophic risk). Third, models of disappointment aversion have tried to capture how individuals react to poor outcomes (e.g., [3] [4] [21] [22] ). In all cases, the arguments lead to non-expected utility models that allow risk preferences to be “non-linear in probabilities”. In this paper, we start with a L_p-Fréchet differentiable preference functional over the probability distribution function of payoff. As showed by Wang [23] , this has two attractive features: 1) it covers a broad class of non-expected utility models; and 2) following Machina [19] , it supports a “local utility analysis” that will prove useful in deriving local results. Our approach includes as a special case rank-dependent utility models that can exhibit non-linearity in the probabilities (e.g., [20] [24] -[27] ). This is relevant in our analysis of the cost of downside risk when these probabilities are associated with unfavorable events.

This paper makes four contributions. The first two contributions were noted above. First, our analysis of the cost of risk and downside risk is presented under a non-expected utility model. This extends previous analyses that have focused on the expected utility model. Second, we propose an additive decomposition of the cost of risk across quantiles, each component identifying the role of risk associated with each quantile. Besides being global and applying “in the large”, this result is useful in the sense that the component of the risk premium associated with lower quantile(s) gives anexplicit measure of the cost of exposure to downside risk. This provides a basis to assess the relative importance of downside risk in the evaluation of the cost of risk³.

Our third contribution is to derive a local measure of the cost of risk associated with each quantile. This measure is approximate and applies “in the small.” It relies on quantile moments to evaluate risk exposure in each quantile⁴. A quantile moment is a moment defined over a specific interval/quantile of the payoff distribution. Our local measure establishes linkages between the cost of risk and quantile moments (including quantile variance and quantile skewness) in each and every quantile. This is of practical value as moments have been commonly used in empirical investigations of risk and downside risk (e.g., [5] [7] [29] -[32] ). Our quantile-based measures generalize previous literature on local risk premium in two directions: 1) they rely on quantile moments across quantiles; and 2) they hold under non-expected utility models (in contrast with many previous analyses of local risk premium that have been obtained under the expected utility model; see [10] [12] [14] [16] [17] ). In this context, we show how quantilevariance and skewness associated with relevant quantiles capture the role of risk located in different intervals of the payoff distribution. This is particularly useful in evaluating the cost and economics of exposure to downside risk (i.e., risk located in the lower tail of the distribution).

Our fourth contribution is to use our local quantile-based measures to examine how departures from the expected utility model affect the risk premium. This is of particular interest when such departures occur for low probability events located in the lower tail of distribution. Our analysis identifies interaction effects between the degree of risk aversion and non-linearity in the probabilities of facing unfavorable events. It shows how departures from expected utility and exposure to downside risk can interact to increase the cost of risk.

2. Quantile-Based Measure of the Cost of Risk

Consider a decision maker facing an uncertain payoff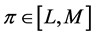. The uncertainty about π is given by the distribution function, where D is the set of all probability functions 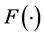over the interval. Throughout the paper, we assume that the interval is bounded.

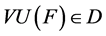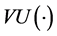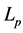Assume that the decision maker’s preferences are represented by the real-valued utility functional. Following Machina [19] and Wang [23] , letting D be equipped with the topology of weak convergence, we assume that is -Fréchet differentiable on D which satisfies with, where V is the class of differentiable functions that are strongly monotonic in payoff⁵. As showed by Wang [23] , the utility functional covers a broad class of non-expected utility models. It includes as special case the rank-dependent utility

model when 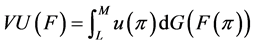where 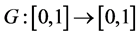is a monotonic increasing function satisfying and 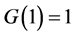(see [20] [23] [24] )⁶. When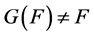, this allows to be non-linear

in the probabilities. As noted by Kaheman and Tversky [2] , Machina [19] and others, this can accommodate several empirical violations of the expected utility model (including the Allais paradox). And when,

this reduces to the expected utility model with, being linear in the probabilities.

Denote the overall mean of by

. (1)

Let be the distribution function of a random payoff with probability amassed at the overall mean payoff when. Then, define the risk premium as the sure amount R satisfying

, (2)

where R is the decision maker’s willingness-to-pay to replace π by its overall mean. Under general risk preferences, the risk premium R in (2) provides a measure of the private cost of risk bearing. Under non-degenerate risk, it can be used to characterize the nature of risk preferences: the decision maker is said to be

when.

In this paper, we explore the economics of exposure to downside risk using a quantile approach. For that purpose, let be some finite integer and consider a sequence satisfying

. Assume that the b_k’s are chosen such that. Denote the k-th interval by, where events in correspond to the risk associated with the k-th interval/quantile,. We will be particularly interested in downside risk associated with the interval located in the lower tail of the distribution.

Define

, (3)

. It follows that is the distribution function obtained from after a stochastic change eliminating the risk below and moving the associated probability mass to the payoff mean. In this context, letting, Equation (3) implies that. And letting, is the distribution function of a degenerate random variable with all probability mass located at point, with when.

Define the mean of π in the interval as

, (4)

. We call m_k1 the k-th quantile mean. Note that the overall mean is a weighted sum of the quantile means m_k1’s:.

Consider the willingness-to-pay to eliminate the risk in the first quantile, moving it to the mean payoff. This willingness-to-pay is defined as the sure amount that satisfies

. (5a)

Next, consider the incremental willingness-to-pay to eliminate the risk of the k-th quantile, moving it the mean payoff while risk has already been eliminated in lower quantiles,. Define this willingness-to-pay as the sure amount that satisfies

. (5b)

for. Note that this sequential elimination of risk across quantiles does affect the mean of the distribution. Indeed, the change in mean payoff going from distribution to is

(5c)

using (4). Equation (5c) makes it clear that eliminating the risk in the k-th quantile (and moving it to) affects mean payoff. Thus, the’s in (5a)-(5b) reflect both risk reductions and mean changes. We are interested in isolating the welfare effect of risk in the above sequential risk elimination scheme. For each quantile k, this can be done by subtracting the change in mean given in (5c) from, as stated next.

Definition: The k-th incremental risk premium is defined as the sure amount that satisfies

, (6a)

By adjusting the willingness-to-pay for the corresponding change in mean payoff, in (6a) can be properly interpreted as the incremental risk premium associated with the elimination of risk in the k-th quantile. The validity and intuition of this interpretation are strengthened from our next result. (See the proof in the Appendix).

Proposition 1: Under the risk preferences, the risk premium R defined in (3) can be decomposed into additive components across quantiles as follows:

, (6b)

where is the incremental risk premium associated with risk in the k-th interval(as defined in (6a)).

Equation (6b) is our first main result. Importantly, it applies under general risk preferences. It includes non-expected utility models, where risk preferences are non-linear in the probabilities. It also includes situations where income effects are present (i.e. where a ceteris paribus change in mean payoff affects willingness-to-pay). In the presence of income effects, the risk premium R and its incremental components’s would be affected by changes in mean payoff⁷. In this case, while the decomposition of the risk premium R given in (6b) remains globally valid, evaluating the cost of risk associated with each quantile becomes more complex⁸. Alternatively, measuring the incremental risk premium would become simpler in the absence of income effects⁹. In this context, the’s would no longer depend on changes in means. And the values taken by each incremental risk premium would be invariant to the ordering of the quantiles in (5a)-(5b).

Equation (6b) shows that the overall risk premium R is equal to the sum of the incremental risk premium’s across all quantiles. As such, (6b) provides a useful decomposition of the risk premium R into additive parts across the K intervals. This decomposition identifies the role of risk exposure in each of the K quantiles. Of special interest is the contribution of to the cost of risk R. Indeed, given, measures the proportion of the risk premium due to exposure to downside risk (i.e., to risk located in the lower quantile).

3. Local Quantile-Based Measures of the Risk Premium

This section explores local measures of the risk premium, with a focus on the decomposition identified in Proposition 1. The analysis proceeds in several steps. In a first step, following Machina [19] and Wang [23] , we explore the linkages between the preference functional and “local utility analysis”. In a second step, we propose to rely on moment-based measurements of risk exposure (including quantile moments). In a third step, we derive local measures of the cost of risk across quantiles.

3.1. Expressing Risk Preferences Using a Local Utility Function

Following Machina [19] and Wang [23] , we first explore how a local utility function can be used to evaluate risk preferences under a general -Fréchet differentiable preference functional. This is stated in the following lemma. (See the proof in the Appendix).

Lemma 1: Given two distribution functions and, there exists a, a distribution function, and a function such that

(7)

where

. (8)

Lemma 1 shows that the welfare effect of a change from to can be measured by the change in expected utility, , based on the utility function defined in

(8). This result is global in the sense that it does not restrict the distribution functions and to be in the same neighborhood of D. From (8), note that the strong monotonicity assumption implies that is

strictly increasing in π and satisfies. As discussed by Machina [19] , is a “local utility function” that provides all the relevant information to evaluate. is lo-

cal in the sense that the distribution function can change with and, thus possibly affecting the impact of π on. Equation (7) indicates that the expected utility model remains useful in the evaluation of risk changes under general conditions. This result applies to non-expected utility models when the preference functional is -Fréchet differentiable (see [19] [23] ). In this case, Lemma 1 shows that we can proceed with our analysis of risk effects using Equations (7)-(8). Note that the expected utility model becomes a special case in situations where the local utility function is globally valid, i.e. where for all.

3.2. Moment-Based Measures of Risk

We have defined the overall mean of π by in Equation (1). We now expand our characterization of risk exposure using moments. First, we denote the j-th central moment of π as

, (9)

Both the variance and skewness have been commonly used in the empirical analysis of risk exposure. As noted above, we want to rely on moment-based measures associated with particular quantiles of the distribution. We defined the k-th quantile mean in (4). In a similar way, we define the j-th central moment of π associated with the k-th interval/quantile as

, (10)

, and In the context of the k-th interval/quantile, is the k-th quantile variance, is the k-th quantile skewness, and more generally is the k-th quantile (central) moment of order j.

Note that quantile moments in (4) and (10) are related to partial moments. First, when, they extend the analysis to an arbitrary number of intervals. Second, following Winkler et al. [35] , define the j-th partial moment in the interval as. For, it follows that. And for, we have, where is the j-th

(non-central) quantile moment in the interval. This shows that (non-central) partial moments are proportional to the corresponding (non-central) quantile moments, the proportionality factor being the probability of

being in the k-th quantile. Noting that and ¹⁰, this establishes the relationship existing between partial moments and quantile moments¹¹.

The central moments given in (1) and (9) as well as the quantile moments, quantile

given in (4) and (10) provide convenient measures of risk exposure. Of special interest are the mean, variance and skewness associated with downside risk, as given by, and in the first quantile. Below, we establish formal linkages between these measures and the cost of risk.

3.3. An Alternative Characterization of the Risk Premium

Our derivation of a local quantile-based measure of the cost of risk is long and tedious. It starts with an alternative representation of the risk premium (presented in lemma 2 below), following a two-step approach. From Equation (2), recall that the risk premium R is the willingness-to-pay to replace the random payoff π by its mean. In a first step, we consider a move where, for each k, π in the k-th interval is replaced by its quantile

mean given in (4), where occurs with probability. In a second step, we consider replacing the quantile means’s by the sure overall mean given in (1).

Consider the first step. Letting, define

, (11)

where the quantile mean is given in (4),. The parameters reflect a change in risk within each quantile. Letting and, note that and when. It follows that a change of from to represents a stochastic shift redistributing risk from π to the quantile means. This shift in risk implied by the function is illustrated in Figure A1.

For a given in (11), let be the distribution function of the payoff given in (11). For a given,the effects of changes in mean payoff on represent a horizon shift in the distribution function, holding the distribution of “deviations from the mean” constant. This is used below in our welfare evaluation as any sure willingness-to-pay corresponds to a horizontal shift in the distribution function. Define as the sure amount satisfying

, (12a)

where is the agent’s willingness to pay to replace the random payoff by. Equation (12a) implies that. And measures the willingness-to-pay to replace π by the quantile means

’s, with occurring with probability.

For given, note that Lemma 1 implies that there exists a distribution function such that Equation (12a) can be alternatively written as

, (12b)

where is defined in (11), and for some.

Next, consider the second step. Letting, define

when. (13)

Note that, and. It follows that a change of s from 1 to 0 represents a redistribution of risk from the’s to the overall mean. This shift in risk implied by the function in (13) is illustrated in Figure A2.

For a given in (13), let be the distribution function of the payoff given in (13). Again, for a given s, the effects of changes in mean payoff on represent a horizon shift in the distribution function. Define as the sure amount satisfying

, (14a)

where is the agent’s willingness to pay to replace the random payoff by. Equation (14a) implies that. And measures the willingness-to-pay to replace the quantile means

’s by the overall mean M, each occurring with probability.

For a given s, Lemma 1 implies that there exists a distribution function such that equation (14a) can be alternatively written as

, (14b)

where is defined in (13) and for some.

Noting that, , , and combining (2), (12a) and (14a), we obtain the following result.

Lemma 2: The risk premium R given in (2) can be decomposed as follows

, (15)

where and satisfy Equation (12) and Equation (14), respectively.

Equation (15) states that the risk premium R can be decomposed into two additive parts: measuring the value of moving the risk in each interval to the corresponding quantile means; and measuring the value of moving the risk from the quantile means to the overall mean. This decomposition will prove useful in deriving a local measure of the risk premium, as discussed below.

3.4. Local Measures

We now proceed with deriving expressions that provide a local approximation of the decomposition of the risk premium given in Proposition 1. Note that, in contrast with the Arrow-Pratt analysis of risk aversion, the linkages between local and global characterizations of downside risk aversion are complex. As noted in the introduction, Keenan and Snow [14] showed that there is no local measure that can give a global characterization of downside risk aversion. Yet, the local characterization of risk aversion and downside risk aversion remains useful as it establishes linkages between the cost of risk and moment-based measures of risk exposure (e.g., [10] [12] [13] ). Below, we derive local measures of the risk premium expressed across quantiles based on the central moments given in (9)-(10).

Our analysis proceeds first with the local measurement of defined in (12a) or (12b) and then with the measurement of defined in (14a) or (14b). Under non-expected utility models, our derivations will rely on (12b) and (14b) and the local utility function given in Lemma 1. In this section, we assume that the local utility function is three times -Fréchet differentiable on ¹².

Under differentiability, we now present an approximate measure of. (See the proof in the Appendix).

Proposition 2: A local measure of the risk premium component is

(16)

where, , , is the quantile variance of π in the interval, and is the quantile skewness of π in the interval.

Equation (16) gives an approximate measure of, the component of the risk premium associated with replacing π in each by its quantile mean, where occurs with probability

.

An approximate measure of is given next. (See the proof in the Appendix).

Proposition 3:A local measure of the risk premium component is

(17)

where, and.

Combining Lemma 2 with Propositions 2 and 3, we obtain the following key result.

Proposition 4: The overall risk premium R can be approximated as

(18)

Equation (18) provides an approximate decomposition of the overall risk premium R in terms of the contribution made by each interval. For the k-th interval, it shows the role of risk preferences (where reflects aversion to variance, and reflects aversion to skewness). Note that these results are consistent with previous research. When there is single interval (K = 1), Pratt [16] , Arrow [17] , and Machina [19] have identified as a local measure of risk aversion. And Crainich and Eeckhoudt [12] , Modica and Scarsini [10] and Jindapon and Nielson [13] have shown that is a local measure of aversion to downside risk. By using a quantile approach, our analysis extends this research by identifying the role of risk aversion and downside risk aversion relative to risk exposure in different intervals/quantiles of the distribution (with K being any integer greater than 1).

Equation (18) also shows how risk exposure across intervals affects the (approximate) cost of risk. It meas-

ures risk exposure by the probability of being in the k-th interval, the quantile mean, the quantile variance, the quantile skewness, and the terms and.

Finally, Equation (18) shows that the overall cost of risk R is (approximately) equal to the sum of the interval-specific cost of risk across all intervals,. This is consistent with the quantile-decomposition of the risk premium presented in Proposition 1. Equation (18) shows how this decomposition can be expressed in terms of quantile moments across quantiles. This is useful to the extent that moments provide a convenient measure of risk exposure.

4. Implications

This section discusses the implications of the quantile-based measures of the risk premium and its decomposition given in Proposition 4. As noted above, our analysis applies under non-expected utility preferences. This section proceeds in three steps. First, we study the implications of Proposition 4 under general risk preferences. Second, we examine the special case where risk preferences satisfy the expected utility model. Third, we evaluate how departures from expected utility affect the cost of risk. The analysis provides new information on the role of downside risk exposure and its effects on the risk premium.

Combining Propositions 1, 2, 3 and 4, we obtain the following result. (See the proof in the Appendix).

Proposition 5: Let V be the class of functions that are differentiable and strongly monotonic in payoff. Then, for all, the k-th component of the risk premium associated with the k-th interval can be approximated as

, (19a)

where

(19b)

(19c)

.

Equations (19a)-(19c) are consistent with the decomposition of the risk premium R given in (6b) (defining satisfying) and in (15) (defining and satisfying).

And they are consistent with the approximations given in (16), (17) and (18). As such, Equation (19b) defining can be interpreted as an approximate measure for the part of associated with moving the risk in the k-th interval to the quantile mean. It includes two additive terms: a variance component (including the quantile variance), and a skewness component (including the quantile skewness).

Each of these terms is weighted by the probability of being in the k-th interval,. The variance component is also weighted by the term, reflecting risk prefe-

rences with respect to variance. Under risk aversion (where), this means that an increase in variance in the k-th interval tends to increase the incremental cost of risk. And the skewness component is

weighted by the term, reflecting risk preferences with respect to

skewness. Under downside risk aversion (where; see [8] ), this implies that an increase in skewness in the -th interval tends to reduce exposure to downside risk and decrease the incremental cost of risk.

Similarly, Equation (19c) defining can be interpreted as an approximate measure for the part of associated with moving the risk from the quantile mean to the overall mean. Again, it in-

cludes two additive terms: a variance component (including the squared deviation from the mean, , and a skewness component (including the cubed deviation from the mean,). Each of these terms is weighted by the probability of being the k-th interval,. The variance component is also weighted by the term, reflecting risk preferences with respect to variance. Under risk aver-

sion (where), this implies that an increase in squared deviation of from the mean tends to increase the incremental cost of risk. And the skewness component is weighted by the term

, reflecting risk preferences with respect to skewness. Under downside risk aversion (where

), this means that an increase in cubed deviation of from the mean tends to reduce exposure to downside risk and decrease the incremental cost of risk.

These results provide useful information on the economics of downside risk. To the extent that most decision makers are averse to downside risk, they provide a way to assess the cost of downside risk exposure. First, since our analysis applies to all intervals’s, it clearly applies to the lowest interval. As such, when, Proposition 5 gives a local measure of the cost of risk associated with the low end of the payoff distribution. Assuming the first interval captures relevant information on downside risk, this measure is useful in evaluating downside risk aversion. Under downside risk aversion, this is the type of risk exposure that may be of greatest concern (e.g., [6] [8] ).

Note that our analysis includes the expected utility model as a special case. Indeed, as noted above, the expected utility model holds when for all, i.e. when the local utility function does not depend on F. Then, the k-th component of the risk premium associated with interval is given by Equations (19b) and (19c) with, To illustrate, consider the case of expected utility where, and belongs to the class of hyperbolic absolute risk aversion utility function:

(20)

Under (20), we have, , and

¹³. Substituting these expressions into (19b)-(19c) shows how our analysis can

be used to provide simple measurements of the component of the risk premium associated with the k-th quantile of the payoff distribution. When focusing on the lowest quantile (), this provides explicit linkages between quantile variance and skewness measures, risk preferences and the cost of exposure to downside risk under the expected utility model. An empirical illustration of the usefulness of the approach is given in Kim et al. [28] , which presents a case study documenting the importance of downside risk in the evaluation of the cost of risk.

More importantly, our analysis applies to non-expected utility models. This corresponds to situations where the local utility function depends on F. As discussed by Machina [19] and Wang [23] , this allows for preferences that are nonlinear in the probabilities, thus relaxing the independence axiom. Our analysis provides new and useful insights on the implications of non-expected utility models for the evaluation of the risk premium. To illustrate, consider the rank-dependent utility model

(21)

where is a differentiable and strictly increasing function, and is a differentiable and strictly increasing function satisfying and. Using integration by parts, (21) can be alternatively written as which implies that

. It follows that, under the rank-dependent utility model (21), the local utility function in (8) can be written as

, (22)

where and. Under differentiability, (22) implies

(23a)

(23b)

where, and,

(23c)

where, and. Equations (23a)-(23c) give the

derivatives of the local utility function associated with the rank dependent utility model (21). Substituting these expressions into (19b)-(19c) provide simple measurements of the (approximate) component of the risk premium associated with the k-th quantile of the payoff distribution. When focusing on the lowest quantile (), this provides linkages between quantile variance and skewness measures, risk preferences and the cost of exposure to downside risk under the rank-dependent utility model (21).

Of special interest here is the case of risk preferences that tend to “overweight” the probability of rare events located in the lower tail of the distribution (e.g., [2] ). As noted by Quiggin ([20] [24] ), Schmeidler [33] , Gonzalez and Wu [36] and others, this oversensitivity to the probabilities of unfavorable events is consistent with the

function in (21) being strictly concave in the interval for some. When, it means that for. Equation (23b) then implies that when

. In this case, compared to the expected utility model (obtained as a special case of (21) when), oversensitivity to rare unfavorable events makes the term more negative. From (19b), this gives an important result: for a risk averse decision maker (with),”overweighting” the probability of rare events located in the lower tail of the distribution tends to increase the effect of the quantile variance m₁₂ on ΔR_a1. The quantile variance in the interval is a measure of exposure to downside risk. We have shown in Proposition 4 and Proposition 5that is a component of the risk premium R. Thus, under risk aversion, our analysis indicates how exposure to downside risk interacts with the sensitivity to rare unfavorable events to increase the risk premium. In particular, our results document how a departure from the expected utility model in the interval S₁ can contribute to increasing the risk premium.

Finally, our investigation also provides useful information on how quantile skewness affects the risk premium. To see that, rewrite Equation (23c) as

(23c’)

Comparing the rank dependent utility model (21) with the expected utility model (obtained when), Equation (23c’) shows how can differ from. This is of special interest when risk preferences exhibit oversensitivity to rare unfavorable events, i.e. when for. Then, the first term on the right-hand side of (23c’) would be positive under the scenario where the “overweighting” of probabilities of events in the lower tail of the distribution declines as payoff increases, i.e. if for ¹⁴. For, the second term on the right-handside of (23’) would also be positive if. But the third term in (23’) would be negative in the (likely) scenario where the probability of events increases as pmoves up from its lower bound L (i.e., if for). Under such scenarios, (23c’) indicates that “oversensitivity” to rare unfavorable events would have ambiguous effects on: it would tend to make larger when the first two terms dominate; but it would make it smaller if the third term dominates. From (19b) evaluated at, we know that the effect of on depends on. Here, is a measure of quantile skewness in the lower interval. It follows that the effects of quantile skewness on depend on both how probabilities vary in and on how the weighting of probabilities varies in the lower tail of the distribution. Since is a component of the risk premium R, this indicates how the quantile skewness (characterizing downside risk in interval) can affect the risk premium R. In the context of the rank-dependent utility model (21), our analysis shows that these effects depend both on the nature of downside risk exposure (e.g. the shape of the distribution function in S₁) and on the (non-linear) way in which probabilities enter risk preferences.

5. Concluding Remarks

This paper has developed a quantile-based analysis of the cost of risk (as measured by the risk premium) reflecting risk exposure across different intervals of the risk distribution. Our analysis applies under general smooth risk preferences. While this includes the expected utility model as a special case, it covers the case of non-expected utility models. Using a quantile-based analysis of the cost of risk, we show how the risk premium can be decomposed into additive components across the range of stochastic outcomes. We identify the components of the cost of risk associated with specific quantiles of the payoff distribution. In this context, the lower quantile(s) correspond to exposure to downside risk, i.e. exposure to unfavorable risky events. This decomposition applies “in the large”. It means that the component(s) of the risk premium associated with the lower quantile(s) provide an assessment of the relative role of downside risk in the evaluation of the cost of risk. Using a quantile approach, we also derive risk premium measures associated with each interval “in the small”. They generalize local measures of risk aversion and downside risk aversion presented in previous research by extending them across multiple intervals of the distribution. We show how quantile variance and skewness across intervals affect the cost of risk.

Finally, we show how departures from the expected utility model affect the risk premium. Our local quantile-based measures identify interaction effects between the degree of risk aversion and non-linearity in the probabilities. They show how risk aversion, departure from the expected utility model and exposure to downside risk interact as they affect the cost of risk.

Note that our paper has focused on the case of risk represented by a distribution function. Extending the analysis to cover situations of uncertainty or ambiguity (where probability assessments may be deemed inappropriate) seems to be a good topic for further research.

Funding

This work was partly supported by the National Research Foundation of Korea Grant funded by the Korean Government (NRF-2014S1A3A2044459).

Cite this paper

Jean-PaulChavas,KwansooKim, (2015) Aversion to Risk and Downside Risk in the Large and in the Small under Non-Expected Utility: A Quantile Approach. Theoretical Economics Letters,05,784-804. doi: 10.4236/tel.2015.56090

References

Appendix

Proof of Proposition 1: Equation (5a) defines DV₁ as the decision maker’s sure willingness-to-pay to eliminate the risk in the first quantile, moving it to the mean payoff. Equation (5b) defines sequentially as the incremental willingness-to-pay to eliminate the risk in the k-th quantile, moving it to the mean payoff while risk has already been eliminated in lower quantiles,. And Equation (6a) defines the incremental risk premium as the willingness-to-pay corrected of the corresponding change in mean

payoff. Noting that from (6a) and that, comparing (5b) with (2) when implies that, as given in (6b). Q.E.D.

Proof of Lemma 1: Following Wang [23] , being -Fréchet differentiable, the mean value theorem implies that there exists a and a distribution function satisfying

Using integration by parts and (8), we obtain

Q.E.D

To prove Propositions 2 and 3, first consider a function. To simplify the notation, we limit our discussion to the case and. Let be a three times continuously differentiable in and strongly monotonic in t, and be three times continuously differentiable. We use subscript letters to denote derivatives, with, , , , , etc.

Lemma 3: Let be the solution of the equation

(A1)

Then,

. (A2)

, (A3a)

(A3b)

(A4)

(A5)

Proof: Evaluated at, (A1) becomes. Since is strongly monotonic in t, this implies (A2).

Differentiating (A1) with respect to s gives

(A6)

Evaluating (A6) at and using (A2) yield

. (A7)

Under the strong monotonicity of f in t (with), (A7) implies (A3).

Differentiating (A6) with respect to s, we obtain

(A8)

Evaluating (A8) at and using (A2) yield

(A9)

Note that, if for all g, then and from (A3b). Then (A9) implies (A4) under the strong monotonicity of f in t.

Differentiating (A8) with respect to s, we obtain

(A10)

Evaluating (A10) at and using (A2) yield

(A11)

Note that, if for all g, then, , , and from (A3b). Then, (A11) reduces to

(A12)

Under the strong monotonicity of f in t (with), (A12) implies (A5). Q.E.D.

Note that lemma 3 has one important implication. If for all g, it shows that affects in (A5), but it does not affect in (A4) nor in (A3). These results will be used below.

Proof of Proposition 2: From Equation (11), we have when, and when. Note that Equation (12b) corresponds to (A1) in lemma 3. It follows from (A2) that. We have

, (A13)

where. Evaluated at, this yields

, (A14)

since from (4).

Note that (A14) implies that for all F. In lemma 3, this corresponds to for all g. From (A3) and (A4) in lemma 3, this gives

, (A15)

and

, (A16a)

(A16b)

And from (A5) in lemma 3, letting and, we obtain

Given from (A15) and, we have when and. It follows that

does not hold, (A17a)

(A17b)

A third-order Taylor series expansion of in the neighborhood of gives

(A18)

where goes to zero faster than as. Using, substituting (A15), (A16) and (A17) in (A18), and using (10), we obtain the desired result. Q.E.D.

Proof of Proposition 3: From (13), we have when, and when.

Note that Equation (14b) corresponds to (A1) in lemma 3. It follows from (A2) that. We have

, (A19)

where. Evaluated at, this yields

, (A20)

for all F. In lemma 3, this corresponds to for all g. From (A3) and (A4) in lemma 3, this gives

, (A21)

and

(A22)

And from (A5) in lemma 3, letting where , and , we obtain

Since and noting that, this gives

(A23)

A third-order Taylor series expansion of in the neighborhood of yields

(A24)

Using and substituting (A21), (A22) and (A23) in (A24), we obtain the desired result. Q.E.D.

Proof of Proposition 5: Under the strong monotonicity of, note that would imply that from (5a)-(5b) and from (6a). Alternatively, when, there exists a utility function exhibiting “non-neutral” risk preferences to the risk located in the interval such that from (5)-(6). Thus, for all, it follows that if and only if.

Similarly, using (8), note that the right-hand side of (19a), (19b) or (19c) is equal to 0 for all if and only if. Combining the above results with (6b), (15), (16) and (17), this establishes that both the right-hand-side and the left-hand-side of (19a) and (19b) correspond to the welfare effects of risk located in the -th quantile. Thiscompletes the proof. Q.E.D.

Given, Figure A1 shows a change of the probability function for in (11) from to. It illustrates that a change from to corresponds to the elimination of the risk in the k-th interval and a move of the associated probability mass to the quantile mean m_k1.

Figure A2 shows a change of the probability function for in (13) from to. It

illustrates that a change from to corresponds to moving the probability mass from the quantile means’s to the overall mean.

NOTES

^*Corresponding author.

¹Under the expected utility model, local measures of downside risk aversion have included the ratio of third to first derivatives of the utility function and the Schwartzian derivative of the utility function (e.g., [10] [12] [14] ).

²As an extension of the Arrow-Pratt approach, the analysis of downside risk aversion has focused on mean-variance preserving spreads of the distribution (e.g., [8] [10] [12] ). As noted by Keenan and Snow [14] and Watt and Vazquez [15] , the associated local measures in general do not provide a global characterization of downside risk aversion.

³For example, although restricted to an expected utility model, Kim et al. [28] used a similar approach to examine the cost of risk on Korean farms. They found evidence that most of the cost of risk can be attributed to exposure to downside risk.

⁴This can be seen as a generalization of the approach used in partial moments. Partial moments evaluate risk exposure based on two quantiles: one below some reference point (lower partial moments), and one above the reference point (higher partial moments). Our quantile-based analysis generalizes partial moments to multiple intervals, each interval corresponding to a different quantile of the payoff distribution. The linkages between partial moments and quantile moments are explored in Section 3.

⁵Strong monotonicity means that first-degree stochastic dominance holds, where for any and satisfying and for all c.

⁶As showed by Wakker [34] , under risk, the rank-dependent utility model coincides with Schmeidler’s Choquet expected utility model [33] . To see that, start with the rank-dependent utility model. Under strongly monotonic preferences and using integration by parts, it can be alternatively expressed as which is the Choquet expected utility model.

⁷An example is the case where a higher expected income is associated with a reduction in the willingness to insure. As analyzed by Pratt [16] under the expected utility model, this would correspond to situations where risk preferences exhibit decreasing absolute risk aversion.

⁸In the presence of income effects, the values taken by each incremental risk premium would be affected by the ordering of the quantiles in (5a)-(5b) and (6a).

⁹For example, under the expected utility model, Pratt [16] showed that absence of income effects corresponds to situations where risk preferences exhibit constant absolute risk aversion.

¹⁰Indeed, using (4), we have. Andwe have, using (4) and.

¹¹In addition, noting that, it follows that the overall j-th (non-central) moment is the weighted sum of the j-th quantile (non-central) moment across all K intervals, with as weight for the k-th interval,

¹²Note that this -Fréchet differentiability assumption can be relaxed. This may be needed in situations where has kinks. This can arise in models exhibiting loss aversion (e.g., [2] ) or disappointment aversion (e.g., [4] ) where the local utility function is continuous in p but exhibits a kink at some threshold payoff. To handle these cases, the -Fréchet differentiability can be relaxed to -Gâteaux differentiability, although at the cost of more restricted approximation properties (e.g., [23] ).

¹³Following Pratt [16] , Arrow [17] and Menezes et al. [8] , this satisfies risk aversion (with) and downside risk aversion (with). And it includes as special cases constant absolute risk aversion (CARA) when, and constant relative risk aversion (CRRA) when.

¹⁴This is a likely scenario given the empirical evidence presented in Kaheman and Tversky [2] .