Theoretical Economics Letters
Vol.05 No.04(2015), Article ID:58828,3 pages
10.4236/tel.2015.54063
Simple Analysis of Dynamic Efficiency in Endogenous Fertility
Kazuki Hiraga
School of Political Science and Economics, Tokai University, Kanagawa, Japan
Email: khiraga581470@gmail.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 July 2015; accepted 14 August 2015; published 17 August 2015
ABSTRACT
This paper compares with two conditions of dynamic (in)efficiency, which is “traditional” and “modified” in overlapped generations (OLG) model with endogenous fertility. We show that both two conditions of dynamic efficiency have a bliss point which maximizes the utility at steady state in endogenous fertility.
Keywords:
Dynamic (In)Efficiency, Overlapped Generations (OLG) Model, Endogenous Fertility

1. Introduction
How many is the fertility rate optimal? This question is interesting in both developed and developing countries. In many advanced countries, they face the aging problem. On the other hand, many developing countries face the population explosion.
This paper investigates the dynamic (in)efficiency in overlapped generation (OLG) model with endogenous fertility. At least, we can evaluate the efficiency at steady state by using OLG model. To evaluate it, we show the two criterions of dynamic efficiency; the one is the “transitional” criteria, which compares with the fertility rate and interest rate. The other is “modified” one, which compares with whether exceeding of “modified” golden rule capital stock which maximizes the utility at steady state.
As for the model with endogenous fertility, there are several seminal literatures. Golosov et al. [1] and Conde- Ruiz et al. [2] analyze the efficiency of the overlapped generation model with endogenous fertility. Although these literatures investigate the efficiency condition, they do not distinguish the difference between the condition of dynamic efficiency with endogenous fertility and without it. Empirically, Abel et al. [3] show that many advanced countries satisfy the dynamic efficiency. Their discussion, however, does not consider about the fertility rate which is one of the major factor of determining the return rate of capital because increasing fertility rate increases the amount of labor and the marginal productivity of capital.
This paper is organized as follows. In Section 2, we introduce the basic model. In Section 3, we evaluate the condition of dynamic efficiency using two criterions and we state the conclusion in Section 4.
2. The Model
We use the model of Grozen et al. [4] without social security mechanism, and relax the assumption of a small open economy. Moreover, we introduce capital stock to investigate the dynamic (in)efficiency in later section.
Similar to Grozen et al. [4] , the economy is populated by a large number of individuals who live for two periods (young and old generations). When they are young; they inelastically supply one unit of labor. Their gross wage income (w) is spent on consumption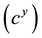 , offspring (n) and is saved for old age (s). That is, we assume
, offspring (n) and is saved for old age (s). That is, we assume
children to be viewed as normal gods. A parent only wants to raise children with a certain level of well-being, i.e. a child is only joyful for its parents if it is assured to receive a particular number of commodities and services. This is reflected in the price p of such a “quality of child”, which is constant and equal for all children in our representative agent model. Moreover, the cost of fertility contains not only price k, but also the opportunity cost of labor; i.e.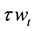 . This cost is come from by the child raising.
. This cost is come from by the child raising.
2.1. The Households
First (young) and second (old) period consumption at t is restricted by the following individual budget constraints,
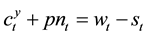 , (1)
, (1)
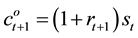 , (2)
, (2)
where 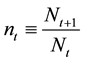 is the gross population growth rate. Therefore, we obtain the lifetime budget constraint,
is the gross population growth rate. Therefore, we obtain the lifetime budget constraint,
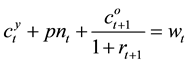 .
.
We assume a representative individual’s utility function as follows,
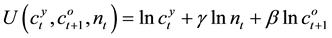 ,
,
where 0 < β < 1 and γ > 0.
In these settings, we solve the individual’s optimization conditions:
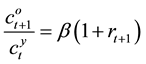 , (3)
, (3)
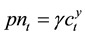 . (4)
. (4)
2.2. The Firms
We set the production function as follows,
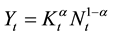 ,
,
where K is the aggregate capital stock and 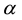 is the share of capital income (0 < α < 1).
is the share of capital income (0 < α < 1).
Output per capita is written as follows,
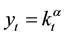
where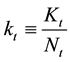 .
.
Then, we obtain the factor price to solve the firm’s profit maximization problem:
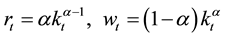 .
.
The capital market clearing condition is written as follows:
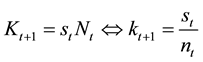 . (5)
. (5)
2.3. Solving the Model
Using Equations (1)-(4) and the factor prices, we can obtain the closed forms,
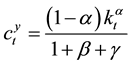 , (6)
, (6)



3. Evaluating Dynamic (In)Efficiency
We check whether the model faces dynamic inefficiency a la Diamond [5] and Tirole [6] to compare with the interest rate and fertility rate which is equal to growth rate. Using above equations, we can obtain the following condition of dynamic inefficiency at steady state:

As 0 < α < 1, Equation (10) shows that there is unique value of 
As you can see, however, this condition does not necessary evaluate efficiency with respect to the utility maximization under endogenous fertility. Then, we re-evaluate the modified condition of dynamic efficiency. We introduce indirect utility function at steady state with respect to capital stock substituting Equations (6), (8) and (9):

Differentiating Equation (11) with respect to k, we obtain the “modified golden rule” capital stock 

Using Equation (12), we obtain the following proposition:
Proposition:
The (per worker) capital stock at steady state is dynamically inefficiency (efficiency) if

We interpret several features in this proposition. First, higher (lower) p widens (narrows) the possibility of dynamic inefficiency, since the capital per worker mitigate and the return rate of capital increases. Second, on the other hand, other parameters do not have monotonic relationship about the possibility of dynamic inefficiency.
4. Conclusion
This paper shows that the two conditions of dynamic (in)efficiency using OLG model with endogenous fertility. We show that both two conditions of dynamic efficiency have a bliss point which maximizes the utility at steady state in endogenous fertility and clarify that the condition of satisfying Pareto efficiency is not consistent with the case in the case that the marginal productivity of capital is larger than growth rate (which is equal to the fertility rate in this paper).
Cite this paper
KazukiHiraga, (2015) Simple Analysis of Dynamic Efficiency in Endogenous Fertility. Theoretical Economics Letters,05,541-544. doi: 10.4236/tel.2015.54063
References
- 1. Golosov, M., Jones, L.E. and Tertilt, M. (2007) Efficiency with Endogenous Population Growth. Econometrica, 75, 1039-1071. http://dx.doi.org/10.1111/j.1468-0262.2007.00781.x
- 2. Conde-Ruiz, J.I., Giménez, E.L. and Pérez-Nievas, M. (2010) Millian Efficiency with Endogenous Fertility. Review of Economic Studies, 77, 154-187. http://dx.doi.org/10.1111/j.1467-937X.2009.00568.x
- 3. Abel, A., Mankiw, G., Summers, L. and Zeckhauzer, R. (1989) Assessing Dynamic Efficiency: Theory and Evidence. Review of Economic Studies, 56, 1-19. http://dx.doi.org/10.2307/2297746
- 4. van Groezen, B., Lees, T. and Meijdam, L. (2003) Social Security and Endogenous Fertility: Pensions and Child Allowance as Siamese Twins. Journal of Public Economics, 87, 233-251. http://dx.doi.org/10.1016/S0047-2727(01)00134-7
- 5. Diamond, P. (1965) National Debt in a Neoclassical Growth Model. American Economic Review, 55, 1126-1150.
- 6. Tirole, J. (1985) Asset Bubbles and Overlapping Generations. Econometrica, 53, 1499-1528. http://dx.doi.org/10.2307/1913232

