Received 20 January 2015; accepted 8 February 2015; published 12 February 2015

ABSTRACT

During periods of high interest rates, businesses utilize their own capital, merge with other businesses, or diversify, and borrow when it is absolutely necessary. People also avoid hardship through refinancing during economic slowdowns because interest rates are low enough to recover some of their income and lower debt interest. High interest rates are more inviting to investments although hard to sustain in the long run. The future looks grim and interest rates have been down for a while, and will probably stay down for some time to come. This paper investigates ways to lower the earnings percentage in interest rates. A new set of the uniform series of the future worth of money involving linear gradients will be mathematically reformulated to investigate the possibility of lowering the interest rate for long term loans and mortgages. A new equation will be formulated and put into a tabulated practical example.

Keywords:

Downscaling: Reducing, Rationalizing and Economizing, Mortgage: A Property Loan, Usually Based on the Value of the Property, Future Value of Money: Value of the Loan or Mortgage with Interest, If Payments Are Timely Made in Full, Present Worth of Money: Amount of the Loan, Mortgage, Compounding: In Finance, Combining Multiples of Payments and Interests

1. Introduction

The interest rate is the main engine that keeps the market-economy moving. Businesses prefer borrowing when the economy is going through a slump and interest rates are low. Companies borrow more during periods of economic slowdowns, either to introduce a new product or to settle up a high interest rate debt.

The future value of money is generated from its current worth in the form of a series of equal payments plus interest. These formulations are simple and easy to manipulate. Upon examining the future value of money in the uniform series compounding of interest rates, it is easy to see the importance of the interest rate and the number of periods in which payments are made and the amount is paid. In order to lower the debt’s value we have to do one of the followings: lowering the interest rate; reducing the number of uniform series payments and/or the amount paid.

Interest rates are established in accordance with a pre-determined agreement that cannot be adjusted or modified. The number of payments is also determined according to a contract that takes into consideration the value of the interest rate itself. However, the amount paid is ascertained on the basis of the interest application to the total number of payments compounded. To clarify this point, interest is actually paid on the principle payments a multiple number of times repetitively and decreases as it approaches the last payment in the series. The main objective of this paper is to lower debt on interest by lowering both the number and amount of loan payments without adjusting or reducing the interest rate.

The essential point is designating a value for the linear gradient based on the total amount of the current worth of the capital, preserving in the process, the conformity of the future worth of the money and its adherence to the rules of the market’s financial regulations. The purpose is to eliminate interest on past principle payments, which is essential to compounding and limiting payments to reach the exact the number of future periodical payments with uncompounded interest rate. The process is purely mathematical but simple and hopefully will be employed in open financial markets. Slumping trend of the world economy may propel bankers in that direction.

2. The Approach

Many methodical financial approaches have been employed in the world of finance, however, they all employ the single payment/uniform series compounding as their basic component. Some approaches emphasize continuous compounding based on monthly, daily or even hourly accounting payments. Other approaches seek higher interest payments with arithmetic or geometric uniform compounding. Greedier plans include continuous arithmetic or geometric interest rates financing.

Uniform series compounding interest equation is the basic element in the formulation of the financial interest rates. The following are lists of employed financial formulas according to related applications:

Single payment compound amount future value formula:

(1)

where 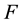is future worth, 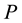the present worth, the interest rate, and 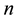is number of years in a loan.

This equation provides us with the future value of a present cost of a loan or current financed item. It is based on a single payment at the end of the loan period. An early payoff may reduce the future value dependent on the contract.

Uniform series compound amount future value:

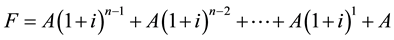(2)

where 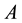is a constant annual payment.

The uniform series compounded payments are made at the end of each period of the loan’s timetable. Equation (3) is a simplified form of Equation (2). It is obvious that increasing 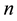and 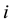increases profit, however, taking into account the context of the contract, it is more likely that such increase leads to lower uniform series payments.

Uniform series compound amount future value (simplified):

(3)

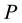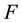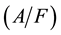Equation (3) can be manipulated using the relationship between the present worth and future worth values and, to produce the present worth, the sinking fund and the capital recovery 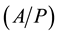values. The Arithmetic gradient series future value:

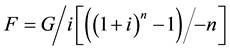(4)

where is the arithmetic gradient.

Equations (4)-(7) employ the same approach with arithmetically or geometrically increasing or decreasing interest, however, the latter is more prevalent. The Arithmetic gradient uniform series value:

(5)

Arithmetic gradient series present value can be formulated using the relationship between the single payment’s future and present worth. For the geometric gradient series case the present worth is:

(6)

where is the geometric gradient.

However, in the case where we have the following for the present worth:

(7)

The total annual payments, in all the previous equations interest included, make up the total future value of the loan. These equations emphasize the multiplicity nature of interest on both the principle payments and their interests. Considering interest rates on a loan with a single principle payment only one interest rate payment will be added to the principle payment emphasizing lower ratio of debt to debt earnings. Multiplicity of interest rate, on the other-hand, stresses the fact that the uniform series compounding system employed in calculating debt earnings is an exaggerated rate of return.

Let us look at an example to demonstrate the multiplicity nature of compound interest. Let us assume that X = $1000 is a loan to be paid up over two years in two equal annual payments. Let us assume that the interest on the loan is 5%. The future value of this loan is

Notice that the annual payment multiplied by the first annual interest rate is now = $1050. By multiplying this value by the 2nd annual interest rate we are actually multiplying the value of the loan and its calculated first annual interest. The loan’s future value is:. This illustrates that the loan’s value has increased by $2.5 over the loan’s initial first annual interest. This small change is the interest on the interest of the first annual loan’s present worth. Now for a loan with a compound interest to be paid over many periods, the periodical interest multiplies and its aggregate increases relatively fast. Now suppose the loan is to be paid over (5, 10, 15, 30 and 60) years with annual interest rates of 5%. Table 1 provides us with the future values and earnings details:

The table illustrates the sizable difference between the future values-earnings over various payment periods. The larger the number of payments periods the larger is the future value. The rate of change of the future value of a loan-mortgage is strongly proportional to increasing the mortgage payment periods. The difference between the earnings more than doubles as we go from 5 to 10 annual payments periods, however, the earnings is five multiples as we go from 30 to 60 payment periods. This emphasizes the unfair banking practices of increasing the number of uniform series of the loan’s payments with lower payment principles, presumably to facilitate and ease the debt’s burden. But in fact, the burden is so much greater it is almost impossible to pay-off the debt in one’s lifetime.

Lowering debt interest may not be on the banking executives’ agenda however, it is one thing consumers in debt aspire for, without refinancing. The obvious solution is to eliminate multiple interests on principle payments. The following technical analysis delves into the derivation and formulation of an equation that may facilitate acquisition of inexpensive, low interest rate loans.

3. Technical Analysis

The following analyses discuss the compounding of interest through simple examples and gradually introduce ways to finding a answers. The process starts with the essentials of the financing in business transactions. Finally, the discussion delves into producing solutions to this paper’s argument.

3.1. Compound Interest Formula

The example in the previous paragraph demonstrate how compounding interest aggregates interest on the entire principle payments, on past and future payments. Once an annual payment is paid, interest on the following annual payments should not be accrued on previous paid principles. Suppose one has a loan with thirty six monthly payments. Suppose these equal monthly payments of $1000 with 5% monthly compound interest rate. The future value of this contract is:

Example 1: the compound interest formula application

So at the end of the last period the debt future value will accumulate to ~$96,000.

Now suppose we find a way to eliminate interest on each preceding principle and include interest accrued from future principle payments. We do this by excluding each paid principle from the calculation of each future payment’s interest at the beginning of each period. Uniform series compounding formulas cannot be reformulated to eliminate compounding of interest on preceding payments’ principles. The following is an illustration of such case.

3.2. Eliminating Multiple Interest in Compound Formula

Take the future value of a loan on the basis of uniform series compound annual payments. Subtract principle of each paid annual payment at the beginning of the next payment we get the following equation:

(8)

Multiplying both sides of Equation (8) by gives:

(9)

By subtracting Equation 8 from Equation (9) and after factoring out and simplifying the outcome we end up with the following:

(10)

Many other forms of the above Equations (8) and (9) were employed for the sake of deriving a viable solution for a financial scheme that leads to a lower pay off of a loan at the same interest rate. However, the final outcome was some form of Equation (10). Equation (10) is almost the same in value as that of the uniform series compound future value Equation (3).

3.3. The New Non-Compound Interest Formula

In order to eliminate the principle from the calculation of future value of loan money we have to utilize a completely different strategy where financial exponentials are completely taken out of the initial formulation.

To do this we have to start by calculating the present worth of Example 1 loan utilized at the beginning of this technical analysis.

The future worth of the loan can also be calculated using the compounding interest rate formula so:

,

So the loan’s present value, $16,547, has multiplied close to six times its value over the 36 years loan; this shark loan’s value at maturity period reached $95,800. There must be a way to lower the earnings so the debt can be handled even at such high rate, and a relatively large number of payments. What if we eliminate the preceding principle after its interest is accrued from following accrued principles’ interests.

The technique to eliminate this interest compounding can be done as follows:

The future worth is always equal to the total amount of the principle payments; that is the present worth plus the interest on the principle payments, which is the interest on the present worth. But we are supposed to eliminate the preceded principle from future accrued interest on following unpaid principle payments. This way we can add interest on each un-accrued principle payment. Now the principle payments in the previous case are 36.

And so we divide the present worth to 36 principle payments.

Now to derive the formula we do the following:

Future worth = present worth + interest on non-accrued principle.

(11)

(12)

The derivation and formulation is in Appendix A1 and Appendix A2

(13)

(14)

(15)

Equation (13) provides us with the future worth of the loan and Equation (14) is the average annual payment, which includes the principle. However, the annual payments, in this technique decrease periodically, as shown in Table 2. So, in order to calculate the annual payments it is preferable to formulate the payments on the basis of their value as part of the future value. Since the future value of a loan is equal to the total annual payments, we can envisage that the annual payments can be derived by utilizing the same methodology employed in the derivation of the future worth of the loan amount. The derivation of the annual payments is in Appendix A2. The summing function of Equation (15) delivers a formula-set representing the annual payments with sequences with the first annual payment at and the last annual payment is, although the formula displays otherwise. The payment can be done using aa forward or backward streaming process.

Figure 1 provides us with a Logarithmic view into the simple relationship between the interest and annual payments. The Figure employs Logarithmic values due to the large disparity in magnitude between the table’s variables.

Where is the future loan value, is the present worth, is the number of payment’s periods, and is the principle payments variable. Now to test this equation we have, , and,

, utilizing Equation (13) we get:

This value can be divided over the estimated number of periods, sub-periods, envisioned for a low annual or monthly payment. The compound interest formula future value would bring hardship to any middle to upper-class family, on monthly basis. On the bases of the above calculation it is appropriate to compare the two methods for a large loan over different loan periods to emphasize the disparity in savings between the two methodologies. Such would amplify the great value of the new technique in future transactions. Let us assume that the amount borrowed is $200,000. This is close to the average amount borrowed for starting a business, buying a house, or making some expensive purchases. Table 3 provides us with ample data comparing the compound interest formula to the new non-compound Interest Formula. Looking at the data on Table 3 we can easily see the difference between future values of Equation 3 and those of Equation (13). The earnings may be much lower for the non-compound interest formula compared to those of the compound interest formula, however, it is the economic situation, nationally and internationally that may determine which is more appropriate.

During the past few years, housing and industrial indices have plummeted to lows unheard of before, considering the size and complexity of today’s world’s economy. The average income has, to a certain extent, gone down as lower income individuals sought higher subsidies and higher income individuals accepted lower bonuses. Borrowing is dependent on people’s ability to recover from debt, and banks’ capacity to overcome large number of bankruptcies. Long term debt with low interest can be serviced by the average income people if the loan is long term and with low interest payments. Equation (13) allows for high interest rates, with low interest payments as Table 3 demonstrates.

Figure 2 compares the earnings with future values of the simple interest formula and those of the compound interest formula. Looking at the chart we can see exponential changes taking place with the compound interest

formula lines, red and blue, while the non-compound values are much smoother. The disparity between the values forced the employment of logarithmic functions to display the four variables on the same screen.

4. Conclusion

The world economy is changing at a faster pace than planned. Few people understand let alone know what is happening on the world stage from an economic point of view. The number of people seeking to improve their income is increasing exponentially; however, the economic-revenue pie is getting larger at a much slower pace. This means that the number of people who will share the future pie is too large. The big businesses, conglomerates, family-owned corporations, rich individuals etc. will have to give up some of their share of the pie for the sake of peace and world tranquility, in other words to keep our world safe and secure. Now, less than one percent of world population own more than 90 percent of world’s income. Within the next twenty years the shift will more likely get worse; the less than one percent will own more than 95 percent. The 99+% of the population will rebel and revolt to get a bigger share of the pie. A much smaller interest rate will have to be utilized to quench both sides. Large profits and exaggerated earnings cannot be the objective of businesses to accumulate revenue, but the means to improve the lives of the common man. Banks should start working on ways to relieve difficulties facing the ordinary men with limited resources. Equation (13) may not produce earnings/profits the way compound interest formulas do, however its application will relieve debt-ridden families and facilitate their acquisition of money. Equations (13)-(15) are the poor men’s ultimate finance equations [1] -[6] .

Cite this paper

Mohammed H. S. AlAshry,11, (2015) Down Scaling Interest in Interest Rate. Theoretical Economics Letters,05,82-91. doi: 10.4236/tel.2015.51012

References

Appendices

Appendix A1

Derivation and formulation of the simple interest formula:

The derivation follows a simple financial logic that focuses on eliminating past previously paid principle from future interest through the elimination of compounding of interest. This means, for example, after completing payments of the first year, future interest covers only future unpaid principle. This way interest is not compounded from one year to the next.

Future worth = present worth + interest on unpaid principle, on annual or monthly based payments.

(a11)

(a12)

But, so the equation becomes

(a13)

(Equation (10)) can be further simplified as follows:

(a14)

Factoring out the interest element we get

(a15)

(Equation (12)) where can be simplified further to

(a16)

The elements in the square parenthesis can be simplified using the summing function to get the following (Equation (13)):

(a17)

Appendix A2

Now formulating the annual payments can be done in the same way the future value is

We know that the average value of the annual payments.

(a21)

However, the annual payments decrease periodically, as shown in Table 2. So, in order to calculate the annual payments it is preferable to formulate the payments on the basis of their value as part of the future value.

Since the future value of a loan is equal to the total annual payments, we can envisage the following:

A_t (total annual payments)

(a22)

Factoring and simplifying (Equation (16)) provides us with the following:

(a23)

The previous equation can be generalized for the total annual payments as follows: the previous equation’s summing can be generalized to include the constant principle payment as part of the annual payment within the summing function providing us with the annual payments equation as given by Equation (15).

(a24)