Theoretical Economics Letters
Vol.04 No.08(2014), Article ID:50790,2 pages
10.4236/tel.2014.48089
A Note on Separability of the Profit Function
Rolf Färe1,2, Giannis Karagiannis3
1Department of Economics, Oregon State University, Corvallis, OR, USA
2Department of Agricultural & Resource Economics, Oregon State University, Corvallis, OR, USA
3Department of Economics, University of Macedonia, Thessaloniki, Greece
Email: rolf.fare@oregonstate.edu, karagian@uom.gr
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 April 2014; revised 5 May 2014; accepted 6 June 2014
ABSTRACT
Based on the concept of translation elasticity we restate in this note the Färe and Grosskopf’s [1] conditions for additive separability of the profit function. We show that for the profit function to be additively separable, the technology must satisfy both simultaneous input-and-output translation homotheticity and graph translation homotheticity.
Keywords:
separability, profit function, directional distance function, graph translation homotheticity, simultaneous input-and-output translation homotheticity

1. Review
Färe and Grosskopf [1] derived conditions on production technology which are required for the profit function to be additively separable into a revenue function component depending only on output prices and a cost function component depending only on input prices. In particular, they showed that simultaneous input-and-output translation homotheticity of production technology implies additive separability of the profit function and vice versa, for some input and output direction vectors such as that the inner product of output prices and the output direction vector is equal to the inner product of inputs prices and the input direction vector. In the light of recent work by Balk, Färe and Karagiannis [2] one can verify that the latter condition implies indeed graph translation homotheticity. We may then restate Färe and Grosskopf’s [1] proposition as following: the profit function is additively separable if and only if technology is simultaneous input-and-output translation homothetic and exhibits graph translation homotheticity.
Let  denote a vector of inputs and
denote a vector of inputs and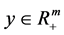 , a vector of outputs with
, a vector of outputs with 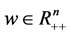 and
and 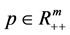 being
being
their corresponding price vectors. The technology is defined in terms of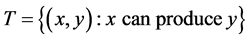 , which is
, which is
closed, allows for free disposability of inputs and outputs, and it contains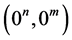 . Then the directional tech-
. Then the directional tech-
nology distance function, which is the negative of the shortage function introduced by Luenberger [3] , is given as (see Chambers, Chung and Färe [4] ):
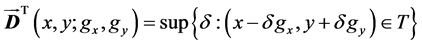
and has the following properties: first, 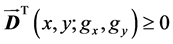 if and only if
if and only if 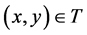 assuming
assuming 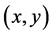 are
are
freely disposable; second, it is non-decreasing in  if inputs are freely disposable; third, it is non-increasing in
if inputs are freely disposable; third, it is non-increasing in 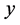 if outputs are freely disposable; fourth, it is concave in
if outputs are freely disposable; fourth, it is concave in 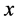 and
and 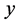 if
if  is convex; fifth,
is convex; fifth,
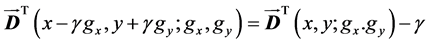 (translation property); and sixth, it is homogeneous of de-
(translation property); and sixth, it is homogeneous of de-
gree −1 in the direction vector
and it contains all other forms of directional functions as special cases. In particular, 

Following Färe and Grosskopf [1] , the technology is simultaneously input-and-output translation homothetic if the directional technology distance function takes the form:

where 

On the other hand, additive separability of the profit function implies that [5] :

In order to prove that (1) implies (2) and vice versa, Färe and Grosskopf [1] had to chose 

that
at a first instance may be seen as a convenient normalization. Nevertheless, based on recent work by Balk, Färe and Karagiannis [2] we can now claim that this is far from being just a convenient normalization. Quite the opposite: it is related to a particular property of production technology, namely graph translation homotheticity. To see this we follow Balk, Färe and Karagiannis [2] in defining the translation elasticity as:

which gives the maximal number of times the output direction vector 

with the corresponding first-order conditions being 


translation elasticity is equal to the relative value of the input and the output direction vector. Then, constant re-
turns to translation in the direction of 


that
[7] showed that in this case

Combining (1) and (4) results in the following form of the directional technology distance function:

We can thus replace the requirement of 
lity of the profit function with that of the last two equalities in (5).
2. Conclusion
In this note we have restated the directional distance function characterization of the technology required for additive separability of the profit function based on the concept of translation elasticity. We have shown in particular that for the profit function to be additively separable, the technology must satisfy both simultaneous input-and-output translation homotheticity and graph translation homotheticity.
References
- Färe, R. and Grosskopf, S. (2000) On Separability of the Profit Function. Journal of Optimization Theory and Applications, 105, 609-620. http://dx.doi.org/10.1023/A:1004693107475
- Balk, B.M., Färe, R. and Karagiannis, G. (2014) On Directional Scale Elasticities. Journal of Productivity Analysis. (forthcoming). http://dx.doi.org/10.1007/s11123-014-0399-6
- Luenberger, D.G. (1995) Microeconomic Theory. McGraw-Hill, New York.
- Chambers, R.G., Chung, Y. and Färe, R. (1998) Profit, Directional Distance Functions, and Nelrovian Efficiency. Journal of Optimization Theory and Applications, 98, 351-364. http://dx.doi.org/10.1023/A:1022637501082
- Lau, L.J. (1972) Profit Functions for Technologies with Multiple Inputs and Outputs. Review of Economics and Statistics, 54, 281-289. http://dx.doi.org/10.2307/1937989
- Chambers, R.G. (2002) Exact Nonradial Input, Output and Productivity Measurement. Economic Theory, 20, 751-765. http://dx.doi.org/10.1007/s001990100231
- Briec, W. and Kerstens, K. (2004)A Luenberger-Hicks-Moorsteen Productivity Indicator: Its Relation to the Hicks- Moorsteen Productivity Index and the Luenberger Productivity Indicator. Economic Theory, 23, 925-939. http://dx.doi.org/10.1007/s00199-003-0403-2


