Theoretical Economics Letters
Vol.2 No.5(2012), Article ID:25807,4 pages DOI:10.4236/tel.2012.25088
Theft and Welfare in General Equilibrium: A Theoretical Note
1Department of Economics, Auburn University, Auburn, USA
2Phoenix Center for Advanced Legal and Economic Public Policy Studies, Washington DC, USA
Email: beardtr@auburn.edu, ford@phoenix-center.org, sternli@auburn.edu, sternml@auburn.edu
Received September 20, 2012; revised October 21, 2012; accepted November 23, 2012
Keywords: General Equilibrium; Theft; Efficiency
ABSTRACT
We show that in a dynamic general equilibrium model theft lowers social welfare even if it is costless to steal, there is no theft prevention cost, and all stolen goods are immediately returned to society. Theft lowers social welfare because it distorts the investment decision, resulting in undercapitalization and a lower steady-state level of capital. This sheds a new light on the literature originated by Tullock [1].
1. Introduction
Although theft of property receives nearly universal condemnation by non-economists, the status of theft in the neoclassical economic framework is far more nuanced. Perhaps the clearest example of this circumstance can be found in the famous exchange between George Stigler and Paul Samuelson concerning the status of what was then termed the “New Welfare Economics”, of which Samuelson [2,3] was an architect and Stigler [4] an early critic. The difficulty, which still haunts such discussions, is really a closely related set of complications which, however, are logically independent. In the first place, when agent A steals something from agent B, the “first-order” welfare consequences are ambiguous: Perhaps B values it more than A did, and theft merely represents another way in which goods are distributed among agents. If money is stolen, then theft might represent a “pure transfer”, i.e. an activity which is assumed to have no welfare consequences. Second, as emphasized by, for example, Tullock [1, p. 230], the “theft industry” attracts resources both as “investments” by thieves (e.g., burglars’ tools), and precautions by potential victims (e.g., burglar alarms and security guards): “This equilibrium, however, would be extremely costly to the society in spite of the fact that the activity of theft only involves transfers. The cost to society would be the investments of capital and labor in the activity of theft and in protection against theft. This lesson has been learned by almost all societies that have adopted a collective method of reducing this sort of income transfer.”
Tullock’s assertion that theft “only involves transfers” echoes the point made much earlier by Stigler [4, p. 356]: “If these theorems are applied to the problem of international trade, for example, they show that income (of all countries together) is maximized by free trade”; and criticized later by Samuelson [2, p. 606]: “This lack of emphasis explains the occurrence of what can only be a momentary lapse, which leads the author (Stigler) to state that ‘income (of all countries together) is maximized by free trade’. Aside from the meaningless statement in the parentheses, the statement is wrong from almost any point of view...” More recently, one can see a reprise of many of these same issues in the reception of Kaplow and Shavell’s “Fairness versus Welfare” [5], which proposes that legal analysis be based solely on consequentialist welfare arguments, rather than deontological principle, as in Dolinko [6] and Dorff [7].
What, then, are economists of a primarily neoclassical bent supposed to conclude about the welfare consequences of theft? Arguments which one might view as relatively persuasive in the partial-equilibrium framework adopted by Tullock [1] are less convincing in the general equilibrium case. If, as claimed, thefts involve “transfers” so that they have no undesirable welfare consequences per se, should the social attitude towards stealing spring primarily (if only partially) from a disapproval of the resources used up to affect it? Is stealing socially undesirable because it is privately costly?
We address this question by including theft within a classic dynamic general equilibrium model. Our analysis is designed to answer a very specific question: Simultaneously supposing that some output is stolen, that theft is costless, that no resources are used up in the act of stealing, and that those who steal the goods value them to precisely the same degree as those who are robbed, does the existence of theft impose any cost on society? The answer, we will argue, is “yes”, and this conclusion arises because theft alters the marginal incentives of producers to produce the good which is stolen, leading to a welfare-dominated sequence of capital investments and lower (Pareto inferior) social outcomes. We conclude that theft is undesirable in a very general sense, and this conclusion is derived within a strictly neoclassical GE framework. Moreover, this conclusion does not depend on the existence of costs of either theft, or theft prevention.
2. A Simple General Equilibrium Model That Incorporates Theft
We adapt the dynamic GE model in Becker [8] to the problem at hand. In this model, an infinitely-lived representative household has perfect foresight, and selects a sequence of consumption and labor supply decisions in order to maximize a discounted sum of utility. The household’s choices are constrained by a typical intertemporal budget constraint, and the capital stock evolves in the conventional manner. The single consumption good is supplied by a competitive industry under constant returns to scale. We are interested in the properties of the consumption path under steady-state conditions, and the relationship of this path to the level of theft in the economy.
Let st denote the amount of the output good stolen in period t that the household receives. The household takes as given the initial capital stock k0, and the sequence of prices of capital services, labor services, and the levels of theft 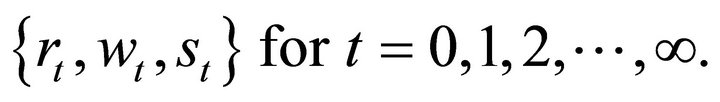 The household chooses the consumption and labor sequences
The household chooses the consumption and labor sequences 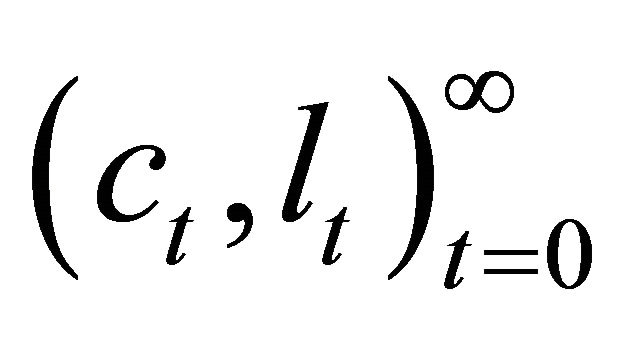 to maximize:
to maximize:
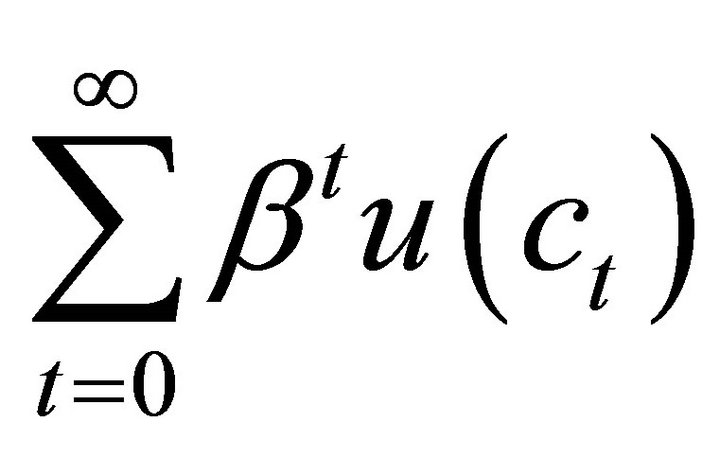 (1)
(1)
subject to the constraints:
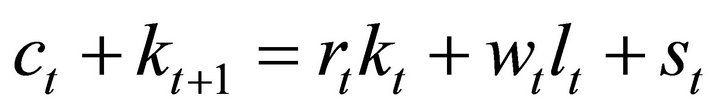 (2)
(2)
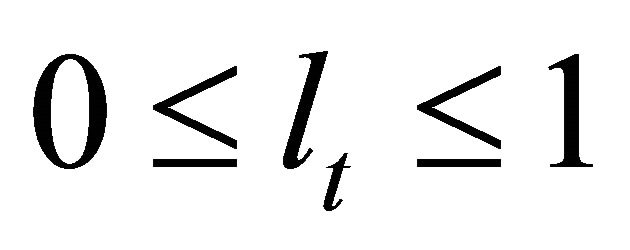 (3)
(3)
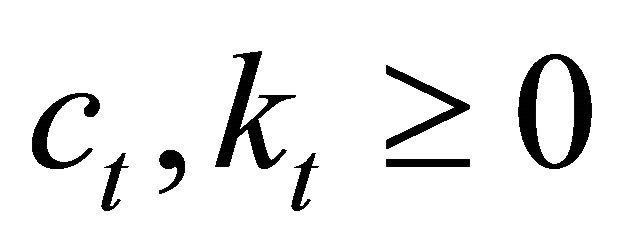 (4)
(4)
where β is the household’s discount factor and u is the household’s instantaneous utility function. The utility function is assumed to be strictly increasing, concave, differentiable, and to have a sufficiently large margin at the origin for interior solutions. The maximal labor supply is normalized to one unit and for simplicity, there is no disutility from work. Hence, 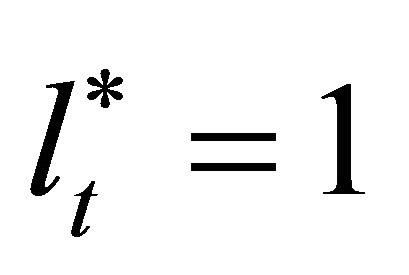 in every period.
in every period.
The household’s problem yields the following Euler equation as a necessary condition:
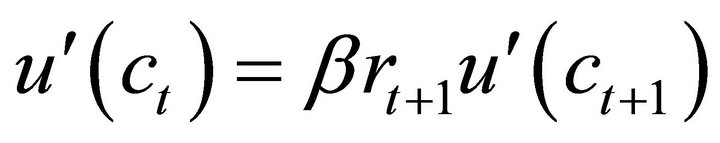 (5)
(5)
In order to illustrate as simply as possible the welfare consequences of theft, we suppose that some fraction θ of the output of the economy is “stolen”, in the sense that the seller is not compensated for it. However, in general equilibrium nothing “disappears”, and the form of the budget constraint given in (2) implies that, in equilibrium, our representative household receives the benefit of the theft in the same manner as it receives other income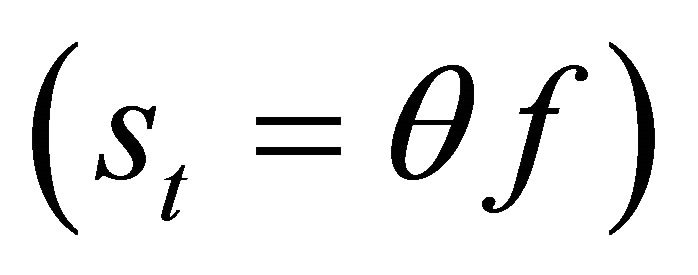 .
.
Thus, the representative competitive firm is assumed to maximize profits given the market prices of labor and capital inputs, and the extent of theft θ in the economy. The firm’s profit (pt) in period t is:
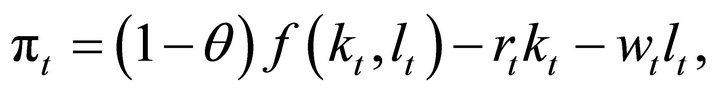 (6)
(6)
where f is the production function which is assumed to be concave, strictly increasing, differentiable, and exhibit constant returns to scale (a common assumption that implies there are no profits in equilibrium, and thus no need to specify the ownership of the firm). Note that theft will decrease the returns to capital and labor, as profit maximization will require the equilibrium conditions 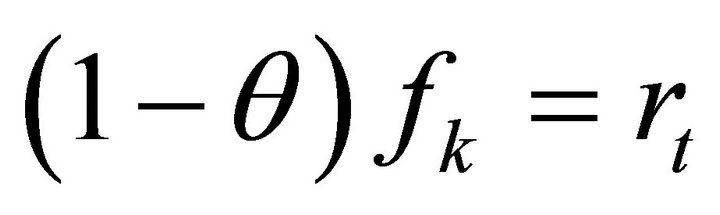 and
and 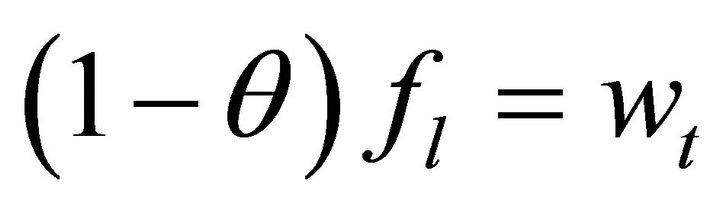 where the subscripts on f indicate marginal products of capital and labor, respectively. If we combine (5) with the marginal condition for profit maximizing with respect to capital, we immediately observe the effect of the distortion caused by theft. We have:
where the subscripts on f indicate marginal products of capital and labor, respectively. If we combine (5) with the marginal condition for profit maximizing with respect to capital, we immediately observe the effect of the distortion caused by theft. We have:
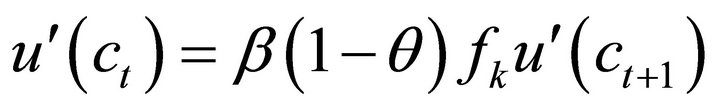 . (7)
. (7)
Equation (7) illustrates the distortionary effect of theft even when the stolen goods are returned to the household without deterioration, theft is costless, and no resources are used up to prevent it. Theft, in effect, is equivalent to a decrease in the discount factor, resulting in greater household impatience and lower levels of capital accumulation, as we will see below.
We consider next the steady state of the economy, in which 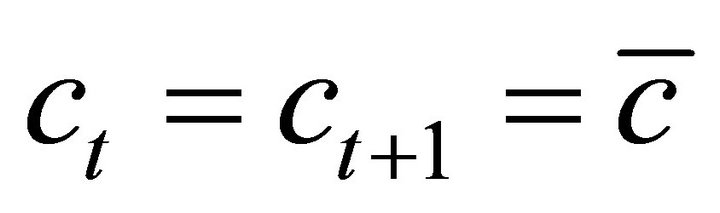 and
and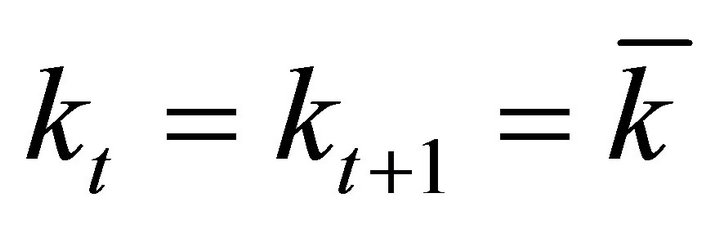 . Equation (7) evaluated at the steady state implies:
. Equation (7) evaluated at the steady state implies:
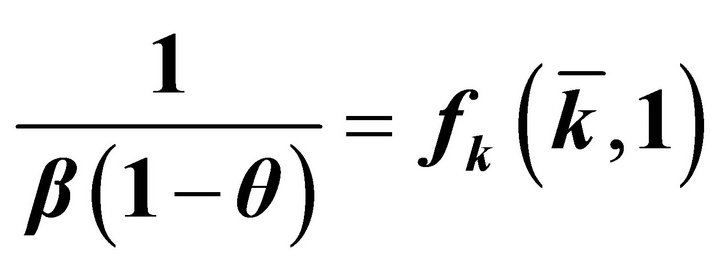 (8)
(8)
Equation (8) has several immediate implications. First, the steady state marginal product of capital is higher the higher is the rate of theft, θ. This in turn suggests that the steady state capital stock is lower in an economy with higher levels of theft, even when theft is costless and fully redistributed to the household. Lower capital also implies lower wages.
How, though, does the prevalence of theft affect the welfare of the household? Using the equilibrium budget constraint we can examine the steady state level of consumption:
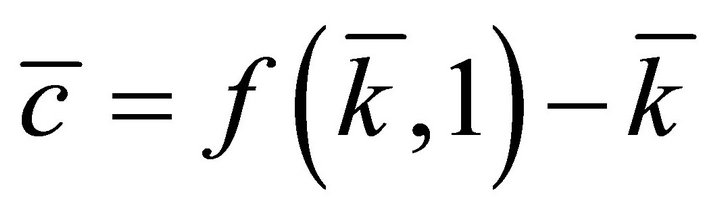 (9)
(9)
Differentiating this expression with respect to the steady state capital level and utilizing the expression for the marginal product of capital in Equation (8) yields:
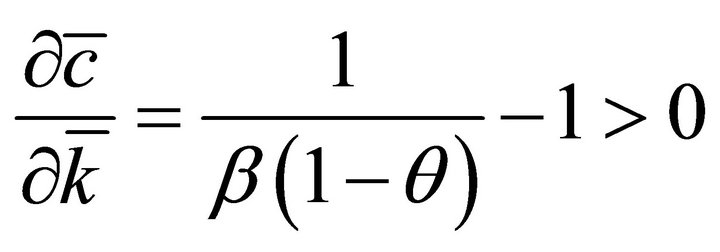 (10)
(10)
The decrease in the steady state capital stock resulting from the theft causes a decrease in the steady state level of consumption. The theft operates like an increase in consumer impatience, generating an increase in initial consumption, decrease in capital, and an ultimate decline in the long-run level of consumption. The remaining question is whether the change in the consumption stream causes a decrease in overall lifetime utility.
To resolve this question, we need to find an optimal growth model formulation which is equivalent to the general equilibrium problem above. Becker [8] establishes that dynamic equilibria of the type described above are mathematically equivalent to optimal growth models which utilize the modified discount factor 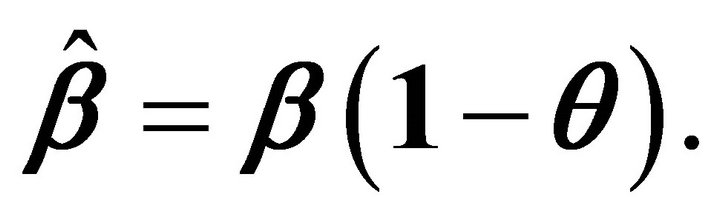 The corresponding optimal growth problem is given by:
The corresponding optimal growth problem is given by:
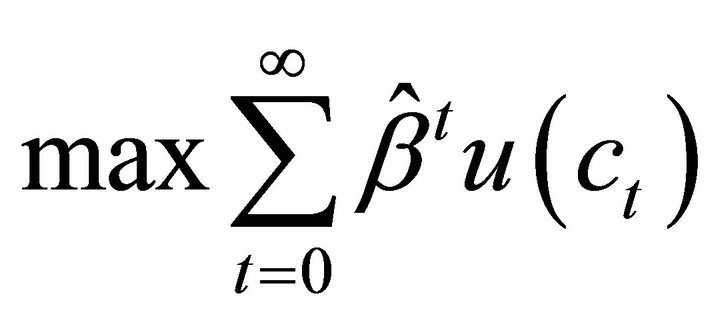 (11)
(11)
subject to the constraints:
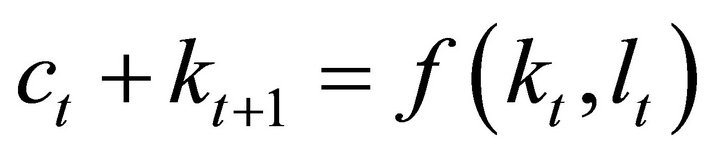 (12)
(12)
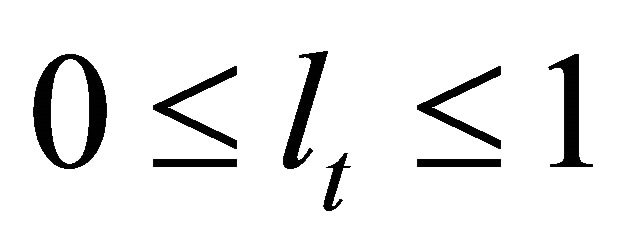 and
and 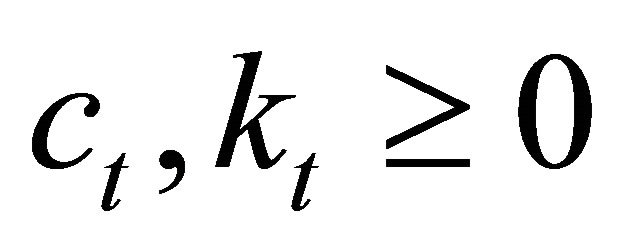 (13)
(13)
The optimal growth problem described in (11)-(13) has exactly the same feasible set as the problem with the true discount factor and this fact has immediate implications. Suppose that some sequence of consumption  is optimal for the planning problem with the discount factor
is optimal for the planning problem with the discount factor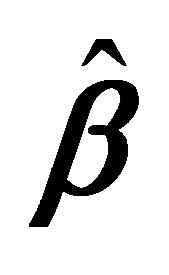 . The
. The  sequence is also feasible for the “true” discount factor β. Yet, since
sequence is also feasible for the “true” discount factor β. Yet, since  is clearly distinct from the optimal path with β as the discount factor, we conclude that the presence of theft, even costless theft that is returned fully to society, leads to a reduction in the lifetime utility of the representative household.
is clearly distinct from the optimal path with β as the discount factor, we conclude that the presence of theft, even costless theft that is returned fully to society, leads to a reduction in the lifetime utility of the representative household.
3. Concluding Remarks
Welfare economics has presented a number of important (and not so important) puzzles over the last sixty years. One puzzle, which has persisted for a long time in a variety of literatures influenced by Tullock’s famous paper on rent-seeking and welfare, concerns the precise reasons why “theft is bad”, at least in some credible, neoclassical welfare calculation. This problem is, indeed, a bit harder than it seems because there are many ways in which theft might impact welfare. Many commentators have noted that costly activities intended to facilitate theft, or to prevent it, will reduce welfare at least compared to cases where theft does not occur, so long as that theft does not somehow reallocate resources to those who value them more. Certainly there is a tradition, made explicit in Tullock [1] that theft is “a transfer”. Be this as it may, it is fair to say that everybody except economists (and presumably thieves) is reasonably convinced that theft is a bad thing in some aggregative, global sense. For example, Siwek [9] estimates that piracy in the copyright industry alone costs the US economy $58 billion in aggregate output each year.
We show in this note that everybody is correct. This conclusion is more useful than might be apparent, however, because we explicitly ignore certain costs that might be associated with theft, which, if included, might “tilt the board” in favor of finding that theft is indeed a bad thing. In particular, we assume throughout that the level of theft is exogenous (so one need not worry about affecting it), that theft is costless to undertake, and no expenditures occur to prevent it, and that the goods thus stolen are immediately and costlessly returned to “society” (our representative household), who benefits fully from it. Even with all of these assumptions, each of which might be viewed as favoring a finding that theft is socially costless, we find a persistent distortion caused by theft which leads to undercapitalization and lower social welfare within an analytic framework that is widely used in economic theory. Utilizing an idea from Becker [8], we demonstrate that the existence of theft acts to distort the investment decision in a manner similar to that arising from more aggressive discounting of the future.
Our analysis supports the general social taboo associated with theft, and it does this on purely neoclassical grounds. Theft can be viewed as a form of societal impatience, with all of the associated dynamic implications. In this way we hope to retire one of the perennially misunderstood aspects of the “New Welfare Economics”, with all due respect to the late George Stigler.
REFERENCES
- G. Tullock, “The Welfare Costs of Tariffs, Monopolies and Theft,” Western Economic Journal, Vol. 5, No. 3, 1967, pp. 224-232.
- P. Samuelson, “Further Commentary on Welfare Economics,” American Economic Review, Vol. 33, No. 3, 1943, pp. 604-607.
- P. Samuelson, “The Gains from International Trade,” Canadian Journal of Economics and Political Science, Vol. 5, No. 2, 1939, pp. 195-205. doi:10.2307/137133
- G. Stigler, “The New Welfare Economics,” American Economic Review, Vol. 33, No. 2, 1943, pp. 335-359.
- L. Kaplow and S. Shavell, “Fairness versus Welfare,” Harvard University Press, Cambridge, 2002.
- D. Dolinko, “Review Essay: The Perils of Welfare Economics,” Northwestern Law Review, Vol. 97, No. 1, 2002, pp. 351-393.
- M. B. Dorff, “Why Welfare Depends on Fairness: A Reply to Kaplow and Shavell,” Southern California Law Review, Vol. 75, 2002, p. 847.
- R. Becker, “Capital Income Taxation and Perfect Foresight,” Journal of Public Economics, Vol. 26, No. 2, 1985, pp. 147-167. doi:10.1016/0047-2727(85)90002-7
- S. Siwek, “The True Cost of Copyright Industry Piracy to the US Economy,” Policy Report #189, Institute for Policy Innovation, 2007.

