ABSTRACT

In this paper, we introduce the stochastic correlation processes for modeling the credit spread. We first model the components of spread process as correlated Ornstein-Uhlenbeck processes and correlation as Jacobi process. Using the properties of Jacobi process, we are able to obtain the analytical solutions for the credit spread option prices. To further enhance the model’s ability to capture the abrupt changes in the observed correlation time series, we construct a new model where the correlation is modeled by a Jacobi process time change by Lévy subordinators. We employ the eigenfunction expansion me- thods to obtain the closed-form solutions for the option prices. Our empirical study indicates the time changed Jacobi process fits the correlation series significantly better than the Jacobi process.

Keywords:

Stochastic Correlation, Jacobi Process, Stochastic Time Change, Eigenfunction Expansion, Credit Spread Options

1. Introduction

A credit spread option is an option on a particular borrower’s credit spread. The credit spread is the difference between the yield on the borrower’s debt and the yield on Treasury debt of the same maturity. The credit spread represents the risk premium that the market demands for holding the borrower’s debt. Unlike the credit default swaps, the payoff of credit spread options depends solely on the measurement of the credit spread rather than a specific credit event. Credit spread options protect the holder of the borrower’s debt from the loss of the rising yield spread due to default or credit rating downgrade.

Most of the models used in the pricing of credit spread options belong to the multi-factor models where state variables are modeled as correlated stochastic processes. [1] proposes a valuation model for pricing credit spread options by assuming that the risk-free interest rate and logarithm of the credit spread follow correlated mean reverting diffusion processes. [2] argues that the spread should be modeled using its two components instead of the spread itself and he extends [1] by assuming that the risk-free rate and the two components of credit spread follow correlated Ornstein-Uhlenbeck (OU) processes. [3] proposes a very general mean reverting process for the credit spread and two stochastic volatility processes, the square-root process and the OU process. The volatility process is assumed to be correlated with the spread process. There are many other examples that employ correlated processes for modeling the credit spread and pricing credit spread options, see e.g. [4] - [9] .

Although most of the models stress the role played by the correlation between state variables for pricing credit spread options, a common assumption is that the correlation is constant. There is a growing literature that documents that the correlation is far from being constant and it should be modeled as a random process, just like interest rate, stock price and volatility. [10] provides analytical properties of the correlation process and provides a new approach of modeling correlation as a stochastic process. [11] and [12] propose a modified Jacobi process to evaluate risk premium of the stochastic correlation and develop a series solution for pricing options under the correlation risk. [13] provides a closed-form approximation for pricing of several two-dimensional derivatives under the assumptions of stochastic correlation. [14] and [15] propose to generate the stochastic correlation process through the hyperbolic transformation of any mean-reverting process with positive and negative values.

In this paper, the main problem we are going to solve is how to model the credit spread and price the credit spread options with the stochastic correlation process. We stress that so far most of stochastic correlation models are developed for the equity and foreign exchange derivatives, where the underlying state variables are usually modeled as correlated geometric Brownian motions. To model the credit spread, we need to take the mean-reversion in the state variables into consideration. In particular, we model the components of the spread process as correlated OU processes and stochastic correlation as Jacobi process which guarantees the correlation between state variables is a bounded process. Using the properties of Jacobi process, we are able to derive the analytical formula for the moments of integrated correlation process required for calculating the credit spread options prices. From the data we employ for the empirical study, we observe that the correlation process changes abruptly and a diffusion model may not fully capture its dynamics. We therefore develop a time-changed model for correlation process where the Jacobi process is time changed by Lévy subordinators to yield state-dependent jumps. To the best of our knowledge, the time-changed Jacobi process (TC-Jacobi) has not been studied in the literature for modeling correlation. We notice that the TC-Jacobi process remains analytically tractable and the closed-form solutions for the credit spread options we derive under the Jacobi process require only minor changes. Our empirical results demonstrate that indeed the TC-Jacobi process improves the fit of correlation process significantly compared to the Jacobi process.

The structure of the paper is as follows. In Section 2, we introduce the credit spread model with constant correlation. In Section 3 we extend the constant correlation model to stochastic correlation model. Using the properties of Jacobi process, we derive the closed-form solutions for credit spread option prices. We introduce the time change to Jacobi process in Section 4 and demonstrate that the analytical formulas remain little changed by employing the eigenfunction expansion method. We compare the performance of Jacobi process with the time changed process using the correlation time series in Section 5. We also numerically study the implications on the derivatives for both processes.

2. A Credit Spread Model with Constant Correlation

Let $\left(\text{Ω},\mathcal{F},P\right)$ denote a probability space with an information filtration ( ${\mathcal{F}}_t$ ). We assume that under physical measure $P$ , the dynamics of the two yields included in the credit spread, denoted by $X_1$ and $X_2$ , follow the correlated OU processes. Thus,

$\text{d}{X}_1\left(t\right)={\kappa }_1\left({\theta }_1-X_1\left(t\right)\right)\text{d}t+{\sigma }_1\text{d}{B}_1\left(t\right),$ (1)

$\text{d}{X}_2\left(t\right)={\kappa }_2\left({\theta }_2-X_2\left(t\right)\right)\text{d}t+{\sigma }_2\text{d}{B}_2\left(t\right),$ (2)

and

$\text{d}{B}_1\left(t\right)\text{d}{B}_2\left(t\right)=\rho \text{d}t,$ (3)

where ${\kappa }_1,{\theta }_1,{\sigma }_1,{\kappa }_2,{\theta }_2,{\sigma }_2\in ℝ$ . $B_1\left(t\right)$ and $B_2\left(t\right)$ are two dependent Brownian motions with constant correlation coefficient $\rho$ .

To price the credit spread options, we need to work under the risk-neutral measure $Q$ . We assume that under the measure $Q$ , the stochastic processes of $X_1\left(t\right)$ and $X_2\left(t\right)$ are still correlated Ornstein-Uhlenbeck processes, but with different coefficients to highlight the risk premium. Therefore,

$\text{d}{X}_1\left(t\right)={\kappa }_1^Q\left({\theta }_1^Q-X_1\left(t\right)\right)\text{d}t+{\sigma }_1\text{d}{B}_1^Q\left(t\right),$ (4)

$\text{d}{X}_2\left(t\right)={\kappa }_2^Q\left({\theta }_2^Q-X_2\left(t\right)\right)\text{d}t+{\sigma }_2\text{d}{B}_2^Q\left(t\right),$ (5)

and

$\text{d}{B}_1^Q\left(t\right)\text{d}{B}_2^Q\left(t\right)=\rho \text{d}t.$ (6)

Under the above assumptions, we know that at time T, under the measure Q the vector $X\left(T\right)=\left(X_1\left(T\right),X_2\left(T\right)\right)$ has a bivariate normal distribution with mean $\mu$ and covariance matrix $\Sigma$ given by

$\mu =\left(\begin{array}{c}{\mu }_1\\ {\mu }_2\end{array}\right),\Sigma =\left(\begin{array}{cc}{\eta }_1^2& {\eta }_{12}\\ {\eta }_{12}& {\eta }_2^2\end{array}\right),$ (7)

where

${\mu }_1=x_1\left(0\right)\exp \left(-{\kappa }_1^{Q}T\right)+{\theta }_1^Q\left(1-\exp \left(-{\kappa }_1^{Q}T\right)\right),$ (8)

${\mu }_2=x_2\left(0\right)\exp \left(-{\kappa }_2^{Q}T\right)+{\theta }_2^Q\left(1-\exp \left(-{\kappa }_2^{Q}T\right)\right),$ (9)

${\eta }_1^2=\frac{{\sigma }_1^2}{2{\kappa }_1^Q}\left(1-\exp \left(-2{\kappa }_1^{Q}T\right)\right),{\eta }_2^2=\frac{{\sigma }_2^2}{2{\kappa }_2^Q}\left(1-\exp \left(-2{\kappa }_2^{Q}T\right)\right),$ (10)

and

$\begin{array}{c}{\eta }_{12}={\sigma }_1{\sigma }_2{\displaystyle {\int }_0^T\exp \left(-\left({\kappa }_1^Q+{\kappa }_2^Q\right)\left(T-s\right)\right)\text{d}s}\\ =\frac{{\sigma }_1{\sigma }_2}{{\kappa }_1^Q+{\kappa }_2^Q}\left(1-\text{exp}\left(-\left({\kappa }_1^Q+{\kappa }_2^Q\right)T\right)\right).\end{array}$ (11)

Let $C\left(T,K,\rho \right)$ denote the price of a call option on credit spread with strike price $K$ and maturity $T$ . The option price can be calculated from

$C\left(T,K,\rho \right)=\exp \left(-rT\right)E^Q\left[\left(X_1\left(T\right)-X_2\left(T\right)-K\right)1_{\left\{X_1\left(T\right)-X_2\left(T\right)>K\right\}}\right],$ (12)

where $\rho$ is included in $C$ to highlight that option price depends on the correlation coefficient $\rho$ . $r$ is the risk-free short rate and for simplicity, we assume it is a constant.

Since $\left(X_1\left(T\right),X_2\left(T\right)\right)$ follows a bivariate normal distribution, we know that $X_1\left(T\right)-X_2\left(T\right)$ is a Gaussian process with mean ${\mu }_1-{\mu }_2$ and variance

${\eta }_s^2={\eta }_1^2+{\eta }_2^2-2\rho {\eta }_{12}.$ (13)

It becomes straightforward to compute the call option prices. We summarize the result in the following proposition (see also [2] and [12] ).

Proposition 1. Assume the dynamics of $X_1$ and $X_2$ are given by (4), (5) and (6) then the option price $C\left(T,K,\rho \right)$ can be calculated by

$C\left(T,K,\rho \right)=\exp \left(-rT\right)\left[\left({\mu }_1-{\mu }_2-K\right)N\left(d\right)+\frac{{\eta }_s}{\sqrt{2\text{π}}}\text{exp}\left(-\frac{d^2}{2}\right)\right],$ (14)

where $d=\frac{{\mu }_1-{\mu }_2-K}{{\eta }_s}$ . $N(\cdot )$ is the CDF of standard normal distribution.

3. Stochastic Correlation with Jacobi Process

3.1. Motivation for Stochastic Correlation Process

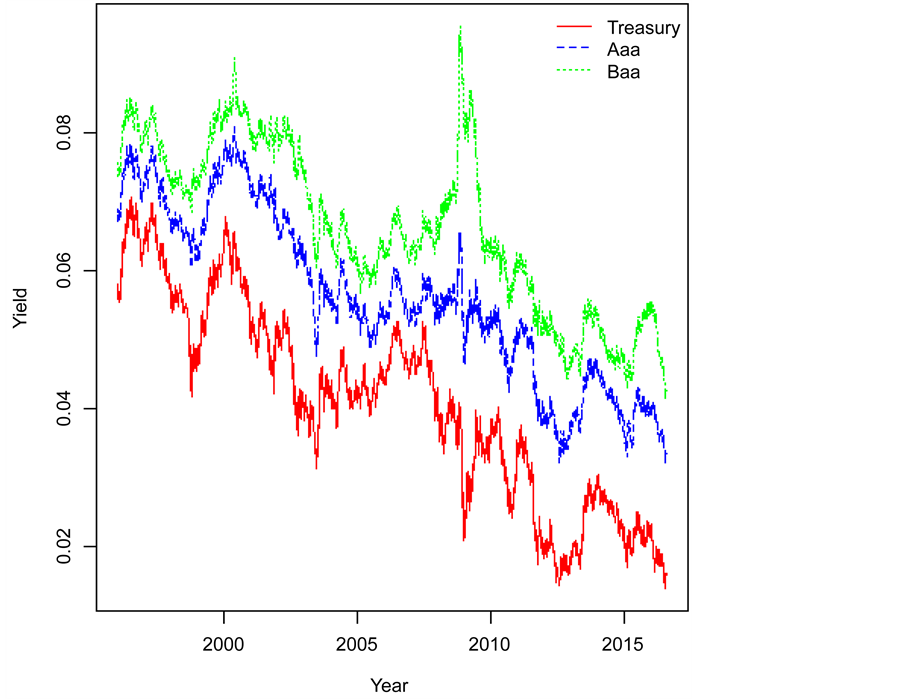
In this section, we extend the constant correlation model in Section 2 by modeling the correlation coefficient $\rho$ as a stochastic process. To motivate our model, we first take a look at the data we use in the empirical study. Our data contain daily rates for 10-year constant maturity Treasury bonds and Moody’s Aaa and Baa seasoned bond indices. The data cover the period January 2, 1996 to July 25, 2016, for a total of 5146 observations. In Figure 1, we plot the time series of three yields and it is clear that all of them display mean reversion. We also construct the time series of correlation by the following procedure (similar to [10] [14] and [15] ):

1) At time $t$ , we regress daily changes in the values of $X_1\left(t\right)$ and $X_2\left(t\right)$ on the values of $X_1\left(t\right)$ and $X_2\left(t\right)$ a day before for a time window $n_T$ :

$\Delta X_1\left(t\right)=X_1\left(t\right)-X_1\left(t-\Delta t\right)={\alpha }_1+{\beta }_1{X}_1\left(t-\Delta t\right)+{\epsilon }_1\left(t\right)$ (15)

and

$\Delta X_2\left(t\right)=X_2\left(t\right)-X_2\left(t-\Delta t\right)={\alpha }_2+{\beta }_2{X}_2\left(t-\Delta t\right)+{\epsilon }_2\left(t\right).$ (16)

2) The correlation $\rho \left(t\right)$ is calculated by the correlation coefficient between ${\epsilon }_1\left(t\right)$ and ${\epsilon }_2\left(t\right)$ for a time window $n_T$ , that is

$\rho \left(t\right)=\frac{{{\displaystyle \sum }}_{i=1}^{n_T}\left({\epsilon }_1\left(t-i\Delta t\right)-{\bar{\epsilon }}_1\left(t\right)\right)\left({\epsilon }_2\left(t-i\Delta t\right)-{\bar{\epsilon }}_2\left(t\right)\right)}{\sqrt{{{\displaystyle \sum }}_{i=1}^{n_T}{\left({\epsilon }_1\left(t-i\Delta t\right)-{\bar{\epsilon }}_1\left(t\right)\right)}^2{{\displaystyle \sum }}_{i=1}^{n_T}{\left({\epsilon }_2\left(t-i\Delta t\right)-{\bar{\epsilon }}_2\left(t\right)\right)}^2}},$ (17)

where ${\bar{\epsilon }}_1\left(t\right)=\frac{1}{n_T}{{\displaystyle \sum }}_{i=1}^{n_T}{\epsilon }_1\left(t-i\Delta t\right)$ and ${\bar{\epsilon }}_2\left(t\right)=\frac{1}{n_T}{{\displaystyle \sum }}_{i=1}^{n_T}{\epsilon }_2\left(t-i\Delta t\right).$

We then roll over to time $t+\Delta t$ and so on to obtain a series of correlations through the time.

In Figure 2 we plot the dynamics of $\rho \left(t\right)$ with $n_T=30$ . We can see clearly that the correlation is far from being constant and it varies very abruptly. The correlation is supposed to be bounded between −1 and 1, but in our dataset, it is concentrated on [0, 1]. In addition, the correlation process displays strong mean-reverting property. In Table 1, we provide the summary statistics for $\rho \left(t\right)$ calculated from the two defaultable bond indices. The average correlations between the yields of Treasury bonds and Aaa and Baa bonds are around

0.87, but the correlations fluctuate between 0.33 and 0.99. The density functions for the correlation series have negative skewness and fat tail.

To satisfy the properties of the correlation series displayed in our data, we model the correlation as a Jacobi process, which takes the value between ${\rho }_m$ and ${\rho }_M$ , i.e.

$\rho \left(t\right)={\rho }_m+\left({\rho }_M-{\rho }_m\right)Y\left(t\right),$ (18)

and

$\text{d}Y\left(t\right)=\kappa \left(\theta -Y\left(t\right)\right)\text{d}t+\sigma \sqrt{Y\left(t\right)\left(1-Y\left(t\right)\right)}\text{d}B\left(t\right),$ (19)

where $\kappa >0$ , $\sigma >0$ and $0<\theta <1$ . $B\left(t\right)$ is a standard Brownian motion and independent of $B_1\left(t\right)$ and $B_2\left(t\right)$ in (1) and (2).

Under the martingale measure $Q$ , we assume the stochastic process of $Y\left(t\right)$ is

$\text{d}Y\left(t\right)={\kappa }^Q\left({\theta }^Q-Y\left(t\right)\right)\text{d}t+\sigma \sqrt{Y\left(t\right)\left(1-Y\left(t\right)\right)}\text{d}{B}^Q\left(t\right),$ (20)

where ${\kappa }^Q>0$ , ${\kappa }^Q>0$ and $0<{\theta }^Q<1$ . $B^Q\left(t\right)$ is a standard Brownian motion under the measure $Q$ and independent of $B_1^Q\left(t\right)$ and $B_2^Q\left(t\right)$ in (4) and (5).

The standard Jacobi process $Y$ takes values between 0 and 1. Following [16] , we also impose the following conditions to ensure that the boundaries 0 and 1 are inaccessible to the process $Y\left(t\right)$ :

$\frac{{\sigma }^2}{2\kappa }\le \theta \le 1-\frac{{\sigma }^2}{2\kappa },\frac{{\sigma }^2}{2{\kappa }^Q}\le {\theta }^Q\le 1-\frac{{\sigma }^2}{2{\kappa }^Q}.$ (21)

3.2. Properties of Jacobi Process

It is well known that there is no closed-form expression for the transition density for the Jacobi process (see e.g. [17] ). However, the transition density of Jacobi process can be represented in terms of eigenfunction expansions.

From (19), we know the infinitesimal generator $\mathcal{L}$ of Jacobi process is

$\mathcal{L}f\left(x\right)=\kappa \left(\theta -x\right)f^{\prime }\left(x\right)+\frac{1}{2}x\left(1-x\right)f^{″}\left(x\right),$ (22)

where $f$ is transformation function. $f^{\prime }$ and $f^{″}$ are first- and second-order derivatives of $f$ , respectively.

Let $\left\{{\lambda }_n\right\}$ be the eigenvalues of $-\mathcal{L}$ and $\left\{{\psi }_n\right\}$ be the corresponding eigenfunctions, i.e.

$-\mathcal{L}{\psi }_n={\lambda }_n{\psi }_n.$ (23)

We know for the Jacobi process $Y$ defined on $I=\left(0,1\right)$ , the eigenvalues and eigenfunctions can be written as (see e.g. [16] and [17] )

${\lambda }_n=\frac{{\sigma }^2}{2}n\left(n-1+\frac{2\kappa }{{\sigma }^2}\right),$ (24)

and

${\psi }_n\left(x\right)=N_n{P}_n^{\left(\alpha ,\beta \right)}\left(2x-1\right),$ (25)

where $\alpha =\frac{2\kappa \left(1-\theta \right)}{{\sigma }^2}-1,$ $\beta =\frac{2\kappa \theta }{{\sigma }^2}-1$ and

$N_n^2=\frac{{\left(\alpha +\beta +2\right)}_{n-1}\left(2n+\alpha +\beta +1\right)n!}{{\left(\alpha +1\right)}_n{\left(\beta +1\right)}_n},$ (26)

where ${\left(a\right)}_0=1$ , ${\left(a\right)}_n=a\left(a+1\right),\cdots ,\left(a+n-1\right)$ , $n>0$ . $P_n^{\left(\alpha ,\beta \right)}\left(x\right)$ is the Jacobi polynomials defined as

$P_n^{\left(\alpha ,\beta \right)}\left(x\right)=\frac{{\left(\alpha +1\right)}_n}{n!}{}_2{}^{}F{}_1\left(-n,1+\alpha +\beta +n;\alpha +1;\frac{1}{2}\left(1-x\right)\right),$ (27)

where ${}_2{}^{}F{}_1\left(a,b;c;x\right)$ is the hypergeometric function defined by

${}_2{}^{}F{}_1\left(a,b;c;x\right)=\underset{n=0}{\overset{\infty }{{\displaystyle \sum }}}\frac{{\left(a\right)}_n{\left(b\right)}_n}{{\left(c\right)}_n}\frac{x^n}{n!}.$ (28)

The spectral decomposition allows us to find the transition density function of Jacobi process $Y$ as

$p_Y\left(t,y\left(0\right),y\left(t\right)\right)=\pi \left(y\left(t\right)\right)\underset{n=0}{\overset{\infty }{{\displaystyle \sum }}}\exp \left(-{\lambda }_{n}t\right){\psi }_n\left(y\left(0\right)\right){\psi }_n\left(y\left(t\right)\right),$ (29)

where $\pi (\cdot )$ is the stationary density function of Jacobi process $Y$ ,

$\pi \left(y\right)=\frac{y^{\beta }{\left(1-y\right)}^{\alpha }}{B\left(\alpha +1,\beta +1\right)},$ (30)

where $B\left(a,b\right)$ is the Beta function defined by

$B\left(a,b\right)=\frac{\Gamma \left(a\right)\Gamma \left(b\right)}{\Gamma \left(a+b\right)},$ (31)

where $\text{Γ}$ is the standard Gamma function.

The most important property of Jacobi polynomials is that they satisfy the following orthogonality condition (see e.g. [16] ):

Proposition 2.

${\displaystyle {\int }_0^1{P}_n^{\left(\alpha ,\beta \right)}\left(2x-1\right)P_m^{\left(\alpha ,\beta \right)}\left(2x-1\right)\pi \left(x\right)\text{d}x}=\{\begin{array}{ll}\frac{1}{N_n^2},\hfill & n=m\hfill \\ 0,\hfill & n\ne m\hfill \end{array}$ (32)

Using this property, we can immediately have the following results:

Corollary 1. Let $k$ , $k_1$ and $k_2$ be nonnegative integers.

・ If $k<n$ , then ${\displaystyle {\int }_{-1}^1{\left(1+x\right)}^{\beta +k}{\left(1-x\right)}^{\alpha }{P}_n^{\left(\alpha ,\beta \right)}\left(x\right)\text{d}x}=0.$

・ If $k<n$ , then ${\displaystyle {\int }_{-1}^1{\left(1+x\right)}^{\beta }{\left(1-x\right)}^{\alpha +k}{P}_n^{\left(\alpha ,\beta \right)}\left(x\right)\text{d}x}=0.$

・ If $k_1+k_2<n$ , then ${\displaystyle {\int }_{-1}^1{\left(1+x\right)}^{\beta +k_1}{\left(1-x\right)}^{\alpha +k_2}{P}_n^{\left(\alpha ,\beta \right)}\left(x\right)\text{d}x}=0.$

In this paper, we need to compute the following two integrals:

${\displaystyle {\int }_{-1}^1{\left(1-x\right)}^{\alpha +k_1}{\left(1+x\right)}^{\beta +k_2}{P}_n^{\left(\alpha ,\beta \right)}\left(x\right)\text{d}x},$

and

${\displaystyle {\int }_{-1}^1{\left(1-x\right)}^{\alpha }{\left(1+x\right)}^{\beta +1}{P}_n^{\left(\alpha ,\beta \right)}\left(x\right)P_m^{\left(\alpha ,\beta \right)}\left(x\right)\text{d}x},$

where $k_1$ and $k_2$ are two nonnegative integers.

We can prove the following results:

Lemma 1.

(i)

${\displaystyle {\int }_{-1}^1{\left(1-x\right)}^{\alpha +k_1}{\left(1+x\right)}^{\beta +k_2}{P}_n^{\left(\alpha ,\beta \right)}\left(x\right)\text{d}x}=\{\begin{array}{ll}0,\hfill & k_1+k_2<n\hfill \\ a_n\left(\alpha ,\beta ,k_1,k_2\right),\hfill & k_1+k_2\ge n\hfill \end{array}$ (33)

where

$\begin{array}{l}{a}_n\left(\alpha ,\beta ,k_1,k_2\right)\\ =\frac{2^{\alpha +k_1+\beta +k_2+1}\Gamma \left(\alpha +k_1+1\right)\Gamma \left(\beta +k_2+1\right)\Gamma \left(n+1+\alpha \right)}{n!\Gamma \left(\alpha +k_1+\beta +k_2+2\right)\Gamma \left(\alpha +1\right)}\\ \times {}_3{}^{}F{}_2\left(-n,\alpha +\beta +n+1,\alpha +k_1+1;\alpha +1,\alpha +k_1+\beta +k_2+2;1\right),\end{array}$ (34)

where ${}_3{}^{}F{}_2\left(a,b,c;d,e;x\right)$ is the hypergeometric function defined by

${}_3{}^{}F{}_2\left(a,b,c;d,e;x\right)=\underset{n=0}{\overset{\infty }{{\displaystyle \sum }}}\frac{{\left(a\right)}_n{\left(b\right)}_n{\left(c\right)}_n}{{\left(d\right)}_n{\left(e\right)}_n}\frac{x^n}{n!}.$ (35)

(ii)

$\begin{array}{l}{\displaystyle {\int }_{-1}^1{\left(1-x\right)}^{\alpha }{\left(1+x\right)}^{\beta +1}{P}_n^{\left(\alpha ,\beta \right)}\left(x\right)P_m^{\left(\alpha ,\beta \right)}\left(x\right)\text{d}x}\\ =\{\begin{array}{ll}0,\hfill & \left|n-m\right|\ge 2\hfill \\ b_{n,m}\left(\alpha ,\beta \right),\hfill & \left|n-m\right|<2\hfill \end{array}\end{array}$ (36)

where

$b_{n,m}\left(\alpha ,\beta \right)=\underset{s=0}{\overset{n}{{\displaystyle \sum }}}\left(\begin{array}{c}n+\alpha \\ s\end{array}\right)\left(\begin{array}{c}n+\beta \\ n-s\end{array}\right){\left(-1\right)}^{n-s}\frac{1}{2^n}{a}_m\left(\alpha ,\beta ,n-s,s+1\right).$ (37)

Proof. To prove (i), from Corollary 1, we immediately know that for $k_1+k_2<n$ , the integral is clearly zero. For $k_1+k_2\ge n$ , we can use the following formula (see e.g. [18] ):

$\begin{array}{l}{\displaystyle {\int }_{-1}^1{\left(1-x\right)}^{k_1}{\left(1+x\right)}^{k_2}{P}_n^{\left(\alpha ,\beta \right)}\left(x\right)\text{d}x}\\ =\frac{2^{k_1+k_2+1}\Gamma \left(k_1+1\right)\Gamma \left(k_2+1\right)\Gamma \left(n+1+\alpha \right)}{n!\Gamma \left(k_1+k_2+2\right)\Gamma \left(1+\alpha \right)}\\ \times {}_3{}^{}F{}_2\left(-n,\alpha +\beta +n+1,k_1+1;\alpha +1,k_1+k_2+2;1\right).\end{array}$ (38)

To prove (ii), we first use another representation of the Jacobi polynomials,

$P_n^{\left(\alpha ,\beta \right)}\left(x\right)=\underset{s=0}{\overset{n}{{\displaystyle \sum }}}\left(\begin{array}{c}n+\alpha \\ s\end{array}\right)\left(\begin{array}{c}n+\beta \\ n-s\end{array}\right){\left(\frac{x-1}{2}\right)}^{n-s}{\left(\frac{x+1}{2}\right)}^s.$ (39)

Then, we have

$\begin{array}{l}{\displaystyle {\int }_{-1}^1{\left(1-x\right)}^{\alpha }{\left(1+x\right)}^{\beta +1}{P}_n^{\left(\alpha ,\beta \right)}\left(x\right)P_m^{\left(\alpha ,\beta \right)}\left(x\right)\text{d}x}\\ =\underset{s=0}{\overset{n}{{\displaystyle \sum }}}\left(\begin{array}{c}n+\alpha \\ s\end{array}\right)\left(\begin{array}{c}n+\beta \\ n-s\end{array}\right){\displaystyle {\int }_{-1}^1{\left(\frac{x-1}{2}\right)}^{n-s}{\left(\frac{x+1}{2}\right)}^s{\left(x+1\right)}^{\beta +1}{\left(1-x\right)}^{\alpha }{P}_m^{\left(\alpha ,\beta \right)}\left(x\right)\text{d}x}.\end{array}$ (40)

Using Corollary 1, we know that for $\left|n-m\right|\ge 2$ , the above integral will be zero. If $\left|n-m\right|<2$ , we can compute the integral using the definition of function $a_n$ . □

In order to obtain the closed-form solution for the credit spread option prices, we are interested in computing the moments of the following integral

$\bar{Y}\left(T\right)={\displaystyle {\int }_0^{T}Y\left(s\right)\exp \left(\left({\kappa }_1^Q+{\kappa }_2^Q\right)s\right)\text{d}s}.$ (41)

We can prove the following result:

Theorem 1.

$\begin{array}{c}{E}^Q\left[\bar{Y}{\left(T\right)}^n\right]=\frac{n!}{B^n\left(\alpha +1,\beta +1\right)}\frac{1}{2^{n\left(\alpha +\beta +2\right)}}\underset{\left(k_1,\cdots ,k_n\right)\in I^n}{{\displaystyle \sum }}{\displaystyle {\prod }_{j=1}^n{\left(N_{k_j}\right)}^2}\\ \times P_{k_1}^{\left(\alpha ,\beta \right)}\left(2y\left(0\right)-1\right){\displaystyle {\prod }_{j=1}^{n-1}{b}_{k_j,k_{j+1}}\left(\alpha ,\beta \right)a_{k_n}\left(\alpha ,\beta ,0,1\right)}\\ \times {\displaystyle {\int }_0^T{\displaystyle {\int }_{s_1}^T\cdots {\displaystyle {\int }_{s_n}^T{\displaystyle {\prod }_{j=1}^n\exp \left(-{\lambda }_{k_j}\left(s_j-s_{j-1}\right)+\left({\kappa }_1^Q+{\kappa }_2^Q\right)s_j\right)\text{d}{s}_n\cdots \text{d}{s}_1}}}},\end{array}$ (42)

where $s_0:=0$ ,

$I^n=\left\{\left(k_1\cdots k_n\right)\in {\mathbb{Z}}_{+}^n:k_n\in \left\{0,1\right\},\left|k_j-k_{j+1}\right|\le 1,j=1,2,\cdots ,n-1\right\},$ (43)

$\alpha$ , $\beta$ , $N_k$ and ${\lambda }_k$ are assumed to be calculated using the coefficients under the measure $Q$ .

Proof. First, we know

$E^Q\left[\bar{Y}{\left(T\right)}^n\right]=E^Q\left[{\left({\displaystyle {\int }_0^{T}Y\left(s\right)\exp \left(\left({\kappa }_1^Q+{\kappa }_2^Q\right)s\right)\text{d}s}\right)}^n\right].$ (44)

We have

$\begin{array}{l}{E}^Q\left[{\left({\displaystyle {\int }_0^{T}Y\left(s\right)\exp \left(\left({\kappa }_1^Q+{\kappa }_2^Q\right)s\right)\text{d}s}\right)}^n\right]\\ =n!{\displaystyle {\int }_0^T{\displaystyle {\int }_{s_1}^T\cdots {\displaystyle {\int }_{s_n}^T{E}^Q\left[{\displaystyle {\prod }_{j=1}^{n}Y\left(s_j\right)\exp \left(\left({\kappa }_1^Q+{\kappa }_2^Q\right)s_j\right)}\right]\text{d}{s}_n\cdots \text{d}{s}_1}}}.\end{array}$ (45)

Using the eigenfunction expansion for the transition density of Jacobi process $Y$ , we have

$\begin{array}{l}{E}^Q\left[{\displaystyle {\prod }_{j=1}^{n}Y\left(s_j\right)\exp \left(\left({\kappa }_1^Q+{\kappa }_2^Q\right)s_j\right)}\right]\\ ={\displaystyle {\int }_0^1\cdots {\displaystyle {\int }_0^1{\displaystyle {\prod }_{j=1}^{n}y\left(s_j\right)\exp \left(\left({\kappa }_1^Q+{\kappa }_2^Q\right)s_j\right)}}}\\ \times p_Y\left(s_{j-1},s_j,y\left(s_{j-1}\right),y\left(s_j\right)\right)\text{d}y\left(s_1\right)\cdots \text{d}y\left(s_n\right)\\ ={\displaystyle {\sum }_{k_1=0}^{\infty }\cdots {\displaystyle {\sum }_{k_n=0}^{\infty }{\displaystyle {\prod }_{j=1}^n\exp \left(-{\lambda }_{k_j}\left(s_j-s_{j-1}\right)+\left({\kappa }_1^Q+{\kappa }_2^Q\right)s_j\right){\psi }_{k_1}\left(y\left(0\right)\right)}}}\\ \times {\displaystyle {\prod }_{j=1}^{n-1}{\displaystyle {\int }_0^{1}x\pi \left(x\right){\psi }_{k_j}\left(x\right){\psi }_{k_{j+1}}\left(x\right)\text{d}x}}{\displaystyle {\int }_0^{1}x\pi \left(x\right){\psi }_{k_n}\left(x\right)\text{d}x}.\end{array}$ (46)

For the first integral in the above equation,

$\begin{array}{l}{\displaystyle {\int }_0^{1}x\pi \left(x\right){\psi }_{k_j}\left(x\right){\psi }_{k_{j+1}}\left(x\right)\text{d}x}\\ =\frac{N_{k_j}{N}_{k_{j+1}}}{B\left(\alpha +1,\beta +1\right)}\frac{1}{2^{\alpha +\beta +2}}{\displaystyle {\int }_{-1}^1{\left(1-x\right)}^{\alpha }{\left(1+x\right)}^{\beta +1}{P}_{k_j}^{\left(\alpha ,\beta \right)}\left(x\right)P_{k_{j+1}}^{\left(\alpha ,\beta \right)}\left(x\right)\text{d}x}.\end{array}$ (47)

For the second integral,

$\begin{array}{l}{\displaystyle {\int }_0^{1}x\pi \left(x\right){\psi }_{k_n}\left(x\right)\text{d}x}\\ =\frac{N_{k_n}}{B\left(\alpha +1,\beta +1\right)}\frac{1}{2^{\alpha +\beta +2}}{\displaystyle {\int }_{-1}^1{\left(1-x\right)}^{\alpha }{\left(1+x\right)}^{\beta +1}{P}_{k_n}^{\left(\alpha ,\beta \right)}\left(x\right)\text{d}x}.\end{array}$ (48)

Using Lemma 1, we can see that $E^Q\left[{\displaystyle {\prod }_{j=1}^{n}Y\left(s_j\right)\exp \left(\left({\kappa }_1^Q+{\kappa }_2^Q\right)s_j\right)}\right]=0$ if $\left(k_1\cdots k_n\right)\notin I^n$ . Otherwise, we have

$\begin{array}{l}{E}^Q\left[{\displaystyle {\prod }_{j=1}^{n}Y\left(s_j\right)\exp \left(\left({\kappa }_1^Q+{\kappa }_2^Q\right)s_j\right)}\right]\\ =\frac{1}{B^n\left(\alpha +1,\beta +1\right)}\frac{1}{2^{n\left(\alpha +\beta +2\right)}}\underset{\left(k_1\cdots k_n\right)\in I^n}{{\displaystyle \sum }}{\psi }_{k_1}\left(y\left(0\right)\right)\\ \times {\displaystyle {\prod }_{j=1}^{n-1}{N}_{k_j}{N}_{k_{j+1}}{b}_{k_j,k_{j+1}}\left(\alpha ,\beta \right)N_{k_n}{a}_{k_n}\left(\alpha ,\beta ,0,1\right)}\\ \times {\displaystyle {\prod }_{j=1}^n\exp \left(-{\lambda }_{k_j}\left(s_j-s_{j-1}\right)+\left({\kappa }_1^Q+{\kappa }_2^Q\right)s_j\right)}.\end{array}$ (49)

Finally, using the definition of ${\psi }_k$ , we obtain the final result. □

We are also interested in calculating the moments of the following quantity

$\begin{array}{c}\bar{\rho }\left(T\right)=\frac{1}{{\displaystyle {\int }_0^T\exp \left(-\left({\kappa }_1^Q+{\kappa }_2^Q\right)\left(T-s\right)\right)\text{d}s}}\\ \times {\displaystyle {\int }_0^T\rho \left(s\right)\exp \left(-\left({\kappa }_1^Q+{\kappa }_2^Q\right)\left(T-s\right)\right)\text{d}s}\\ ={\rho }_m+\frac{\left({\rho }_M-{\rho }_m\right)\left({\kappa }_1^Q+{\kappa }_2^Q\right)\exp \left(-\left({\kappa }_1^Q+{\kappa }_2^Q\right)T\right)}{1-\exp \left(-\left({\kappa }_1^Q+{\kappa }_2^Q\right)T\right)}\\ \times {\displaystyle {\int }_0^{T}Y\left(s\right)\exp \left(\left({\kappa }_1^Q+{\kappa }_2^Q\right)s\right)\text{d}s}.\end{array}$ (50)

Using binomial expansion, we immediately have

$\begin{array}{l}{E}^Q\left[\bar{\rho }{\left(T\right)}^n\right]\\ =\underset{j=0}{\overset{n}{{\displaystyle \sum }}}\left(\begin{array}{c}n\\ j\end{array}\right){\rho }_m^{n-j}{\left(\frac{\left({\rho }_M-{\rho }_m\right)\left({\kappa }_1^Q+{\kappa }_2^Q\right)\exp \left(-\left({\kappa }_1^Q+{\kappa }_2^Q\right)T\right)}{1-\exp \left(-\left({\kappa }_1^Q+{\kappa }_2^Q\right)T\right)}\right)}^j{E}^Q\left[\bar{Y}{\left(T\right)}^j\right].\end{array}$ (51)

It is also easy to obtain the centered moments of $\bar{\rho }\left(T\right)$ from the uncentered moments. The general equation for converting the n^th uncentered moment to the centered moment is

$\begin{array}{l}{E}^Q\left[{\left(\bar{\rho }\left(T\right)-E^Q\left[\bar{\rho }\left(T\right)\right]\right)}^n\right]\\ =\underset{j=0}{\overset{n}{{\displaystyle \sum }}}\left(\begin{array}{c}n\\ j\end{array}\right){\left(-1\right)}^{n-j}{E}^Q\left[\bar{\rho }{\left(T\right)}^j\right]{\left(E^Q\left[\bar{\rho }\left(T\right)\right]\right)}^{n-j}.\end{array}$ (52)

We provide the first two centered moments for $\bar{\rho }\left(T\right)$ as follows:

Corollary 2.

$\begin{array}{l}{E}^Q\left[\bar{\rho }\left(T\right)\right]\\ ={\rho }_m+\frac{\left({\rho }_M-{\rho }_m\right)\left({\kappa }_1^Q+{\kappa }_2^Q\right)\exp \left(-\left({\kappa }_1^Q+{\kappa }_2^Q\right)T\right)}{1-\exp \left(-\left({\kappa }_1^Q+{\kappa }_2^Q\right)T\right)}\\ \times \frac{1}{B\left(\alpha +1,\beta +1\right)}\frac{1}{2^{\alpha +\beta +2}}\times \underset{k=0}{\overset{1}{{\displaystyle \sum }}}{N}_k^2{P}_k^{\left(\alpha ,\beta \right)}\left(2y\left(0\right)-1\right)a_k\left(\alpha ,\beta ,0,1\right)\\ \times \frac{\exp \left(\left(-{\lambda }_k+{\kappa }_1^Q+{\kappa }_2^Q\right)T\right)-1}{-{\lambda }_k+{\kappa }_1^Q+{\kappa }_2^Q}.\end{array}$ (53)

$\begin{array}{l}Va{r}^Q\left[\bar{\rho }\left(T\right)\right]\\ ={\left(\frac{\left({\rho }_M-{\rho }_m\right)\left({\kappa }_1^Q+{\kappa }_2^Q\right)\exp \left(-\left({\kappa }_1^Q+{\kappa }_2^Q\right)T\right)}{1-\exp \left(-\left({\kappa }_1^Q+{\kappa }_2^Q\right)T\right)}\right)}^2\frac{2}{B^2\left(\alpha +1,\beta +1\right)}\frac{1}{2^{2\left(\alpha +\beta +2\right)}}\\ \times \left(U_1+U_2+U_3+U_4+U_5\right)-{\left(E^Q\left[\bar{\rho }\left(T\right)\right]-{\rho }_m\right)}^2,\end{array}$ (54)

where

$\begin{array}{c}{U}_1=N_0^4{P}_0^{\left(\alpha ,\beta \right)}\left(2y\left(0\right)-1\right)b_{0,0}\left(\alpha ,\beta \right)a_0\left(\alpha ,\beta ,0,1\right)\frac{1}{{\kappa }_1^Q+{\kappa }_2^Q}\\ \times \left[\frac{\exp \left(2\left({\kappa }_1^Q+{\kappa }_2^Q\right)T\right)-\exp \left(\left({\kappa }_1^Q+{\kappa }_2^Q\right)T\right)}{{\kappa }_1^Q+{\kappa }_2^Q}-\frac{\exp \left(2\left({\kappa }_1^Q+{\kappa }_2^Q\right)T\right)-1}{2\left({\kappa }_1^Q+{\kappa }_2^Q\right)}\right],\end{array}$ (55)

$\begin{array}{c}{U}_2=N_0^2{N}_1^2{P}_1^{\left(\alpha ,\beta \right)}\left(2y\left(0\right)-1\right)b_{1,0}\left(\alpha ,\beta \right)a_0\left(\alpha ,\beta ,0,1\right)\frac{1}{{\kappa }_1^Q+{\kappa }_2^Q}\\ \times [\frac{\exp \left(\left(-{\lambda }_1+2\left({\kappa }_1^Q+{\kappa }_2^Q\right)\right)T\right)-\exp \left(\left({\kappa }_1^Q+{\kappa }_2^Q\right)T\right)}{-{\lambda }_1+{\kappa }_1^Q+{\kappa }_2^Q}\\ -\frac{\exp \left(\left(-{\lambda }_1+2\left({\kappa }_1^Q+{\kappa }_2^Q\right)\right)T\right)-1}{-{\lambda }_1+2\left({\kappa }_1^Q+{\kappa }_2^Q\right)}],\end{array}$ (56)

$\begin{array}{c}{U}_3=N_0^2{N}_1^2{P}_0^{\left(\alpha ,\beta \right)}\left(2y\left(0\right)-1\right)b_{0,1}\left(\alpha ,\beta \right)a_1\left(\alpha ,\beta ,0,1\right)\frac{1}{-{\lambda }_1+{\kappa }_1^Q+{\kappa }_2^Q}\\ \times [\frac{\exp \left(2\left({\kappa }_1^Q+{\kappa }_2^Q\right)T\right)-\exp \left(\left(-{\lambda }_1+{\kappa }_1^Q+{\kappa }_2^Q\right)T\right)}{{\lambda }_1+{\kappa }_1^Q+{\kappa }_2^Q}\\ -\frac{\exp \left(2\left({\kappa }_1^Q+{\kappa }_2^Q\right)T\right)-1}{2({\kappa }_1^Q+{\kappa }_2^Q)}],\end{array}$ (57)

$\begin{array}{c}{U}_4=N_1^4{P}_1^{\left(\alpha ,\beta \right)}\left(2y\left(0\right)-1\right)b_{1,1}\left(\alpha ,\beta \right)a_1\left(\alpha ,\beta ,0,1\right)\frac{1}{-{\lambda }_1+{\kappa }_1^Q+{\kappa }_2^Q}\\ \times [\frac{\exp \left(\left(-{\lambda }_1+2\left({\kappa }_1^Q+{\kappa }_2^Q\right)\right)T\right)-\exp \left(\left(-{\lambda }_1+{\kappa }_1^Q+{\kappa }_2^Q\right)T\right)}{{\kappa }_1^Q+{\kappa }_2^Q}\\ -\frac{\exp \left(\left(-{\lambda }_1+2\left({\kappa }_1^Q+{\kappa }_2^Q\right)\right)T\right)-1}{-{\lambda }_1+2\left({\kappa }_1^Q+{\kappa }_2^Q\right)}],\end{array}$ (58)

$\begin{array}{c}{U}_5=N_1^2{N}_2^2{P}_2^{\left(\alpha ,\beta \right)}\left(2y\left(0\right)-1\right)b_{2,1}\left(\alpha ,\beta \right)a_1\left(\alpha ,\beta ,0,1\right)\frac{1}{-{\lambda }_1+{\kappa }_1^Q+{\kappa }_2^Q}\\ \times [\frac{\exp \left(\left(-{\lambda }_2+2\left({\kappa }_1^Q+{\kappa }_2^Q\right)\right)T\right)-\exp \left(\left(-{\lambda }_1+{\kappa }_1^Q+{\kappa }_2^Q\right)T\right)}{{\lambda }_1-{\lambda }_2+{\kappa }_1^Q+{\kappa }_2^Q}\\ -\frac{\exp \left(\left(-{\lambda }_2+2\left({\kappa }_1^Q+{\kappa }_2^Q\right)\right)T\right)-1}{-{\lambda }_2+2\left({\kappa }_1^Q+{\kappa }_2^Q\right)}].\end{array}$ (59)

3.3. Credit Spread Option Prices under Jacobi Process

If $\rho \left(t\right)$ is not a constant, but deterministic, the credit spread $X_1\left(T\right)-X_2\left(T\right)$ defined in Section 2 will still be a Gaussian process with same mean ${\mu }_1-{\mu }_2$ but different variance

${\bar{\eta }}_s^2={\eta }_1^2+{\eta }_2^2-2\bar{\rho }\left(T\right){\eta }_{12},$ (60)

where $\bar{\rho }\left(T\right)$ is defined in (50).

The pricing formula in (14) will be changed to

$C\left(T,K,\bar{\rho }\right)=\exp \left(-rT\right)\left[\left({\mu }_1-{\mu }_2-K\right)N\left(\bar{d}\right)+\frac{{\bar{\eta }}_s}{\sqrt{2\text{π}}}\exp \left(-\frac{{\bar{d}}^2}{2}\right)\right],$ (61)

where $\bar{d}=\frac{{\mu }_1-{\mu }_2-K}{{\bar{\eta }}_s}$ .

If the correlation coefficient $\rho \left(t\right)$ is a stochastic process, but independent of underlying processes for the two yields $X_1\left(t\right)$ and $X_2\left(t\right)$ , we can employ Taylor series expansion method to obtain the analytical formula for the spread credit spread option prices (see e.g. [11] [12] [13] )

$\begin{array}{c}\bar{C}\left(T,K,\bar{\rho }\right)=E^Q\left[C\left(T,K,\bar{\rho }\right)\right]\\ =E^Q\left[\underset{k=0}{\overset{\infty }{{\displaystyle \sum }}}\frac{C^{\left(k\right)}\left(T,K,E^Q\left[\bar{\rho }\right]\right)}{k!}{\left(\bar{\rho }-E^Q\left[\bar{\rho }\right]\right)}^k\right]\\ =\underset{k=0}{\overset{\infty }{{\displaystyle \sum }}}\frac{C^{\left(k\right)}\left(T,K,E^Q\left[\bar{\rho }\right]\right)}{k!}{E}^Q\left[{\left(\bar{\rho }-E^Q\left[\bar{\rho }\right]\right)}^k\right],\end{array}$ (62)