Received 28 February 2015; accepted 22 May 2015; published 26 May 2015

ABSTRACT

Traditionally, portfolio managers have been discouraged from timing the market, for example, equity managers have been forced to adhere strictly to a benchmark with static or relatively stable components, such as the S&P 500 or the Russell 3000. This means that the portfolio’s exposures to all risk factors should mimic as closely as the corresponding exposures of the benchmark. The main risk factor, of course, is the market itself. Effectively, a long-only portfolio would be constrained to have a beta of 1. More recently, however, managers have been given greater discretion to adjust their portfolio’s risk exposures (especially, the beta of their portfolio) dynamically to match the manager’s beliefs about future performance of the risk factors themselves. This freedom translates into the manager’s ability to adjust the portfolio’s beta dynamically. These strategies have come to be known as smart beta strategies. Adjusting beta dynamically amounts to attempting to “time” the market; that is, to increase exposure when one anticipates that the market will rise, and to decrease it when one anticipates that the market will fall.

Keywords:

Active Portfolio Management, Beta, Alpha, Portfolio Optimization, What Is Smart Beta?

1. Introduction

There has been an increasing interest in index strategies or advance beta strategies, which try to generate out performance over the standard market indices. Among those strategies one of the most famous strategies is smart beta. There is $142 billion invested in smart beta funds [1] . There are many definitions for smart beta on Wall Street [2] . One definition is that smart beta is a strategy which attempts to deliver a better risk and return trade-off than conventional market cap weighted indices by using alternative weighting schemes based on measures such as volatility or dividends [3] . But for us, smart beta means a portfolio management strategy which combines the cap weight, economic scale and the minimum variance of the assets in the portfolio. It is only a weighing strategy which replicates the benchmark index.

The origin of smart beta was done by Research Affiliates, and according to Research Affiliates smart beta is a strategy that lies between Passive and Active portfolio management. Passive portfolio management is a strategy in which investment is done with an intention of long term appreciation with minimum maintenance. In Active portfolio management strategies investment is done and the portfolio is continuously monitored using data and research methods in order to exploit profitable conditions [4] .

In order to decide what index we are going to use for our smart beta strategy we referred to the paper Fundamental Indexes [5] which helped to learn how we can build our own index with the help of smart beta strategies. In order to decide the technique of implementing smart beta strategies we referred the paper Beyond Cap weight [6] in which we came up with a strategy of combining Cap Weight, Economic Scale (Fundamental Index) and Minimum Variance. In order to test our strategy we are using the last three-year data for S&P 100 in order to check if we are making more or less money than the market. But the problem that we faced in doing so is that companies come in and go out every quarter in S&P 100 index so the solution for it is if any company goes out, then we consider the economic scale for it to be zero and rescale the resulting economic scale index to make the sum of weights for each quarterly index as 1.

2. Methodology

In order to test the strategy of smart beta, we developed four different portfolios with four different strategies in order to test the results obtained by back testing the new strategies on the different portfolios. We back tested the performance of each portfolio against three-year data (2011-13) for S&P 100. We used the economic scale as one of the key factors for this portfolio. The economic scale approach uses a company’s fundamental economic size, weighting companies according to sales, cash flow, book value and dividends, and then averaging the four measures to assign portfolio weights to each company in an index. Selecting and weighting companies for a stock market index, using fundamental economic measures of company size, was introduced by Arnott and West (2006) [5] . The portfolio resulted from the economic scale will be referred to as the SMART BETA INDEX, it will be referred to as an index because it will be involved in each of the portfolios constructed.

The SMART BETA INDEX is a representative portfolio, weighted to mirror the look and composition of the publicly traded economy. Minimum variance portfolios which we created and mixed with the SMART BETA PORTFOLIOS are designed to reduce portfolio risk by placing more weight on the underlying assets which have minimum volatility in the market [7] . So the price of each underlying asset which makes minimal movements in the market will be given a higher weight in the minimum variance portfolio. In order to make the smart beta portfolios less risky, we have to mix the minimum variance portfolio with the smart beta index. The Cap Wight is considered with the market capitalization of each company (underlying asset), so the weight is distributed accordingly [8] . The company which holds the highest market capitalization in a certain market index will be holding the largest weight in the cap weight portfolio. The cap weight portfolio acts to enhance the performance of the smart beta index since both of them consider the market information of the underlying assets [9] .

Now we created four portfolios and implemented strategies which involved construction of a minimum variance portfolio and our smart beta index on them. We then calculated the returns associated for each portfolio and compared them with each other and the market returns for those particular time periods.

Smart Beta Index for a company:

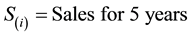
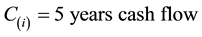
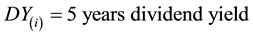
Formula to calculate 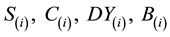as percent

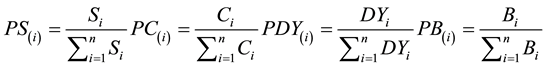(1)

where n is the number of companies that we are investing in (S&P 100)

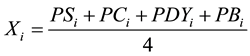(2)

Subject to

(3)

For cap weight

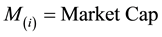(4)

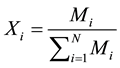(5)

Subject to

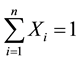(6)

Minimum Variance Portfolio

Minimum variance portfolio is a special case of the linear equality constrained mean-variance portfolio, it is a portfolio obtained by letting the risk tolerance equal to zero. That is, let the investor become completely averse to risk. In this case, minimization of the objective function becomes equivalent to minimization of variance [10]

(7)

Q is the cov matrix,

h are the weights.

We used quadratric programming for Minimum Variance Portfolio.

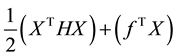(8)

Subject to

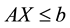(9)

satisfying the equality constraints.

(10)

r is the returns(daily),

X is our weight vector,

H = Q is the covariance matrix of daily returns,

f in this case is equal to zero matrix.

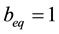(11)

which constraints the sum of X to be 1

We don’t have inequality constraints, lower and upper bounds.

(12)

we add inequality constraints

where the constraint on the returns and total sum of X should be zero, so.

In this case we get a portfolio with a total weight of 1. We also constructed a minimum variance portfolio which has a total weight of zero. We use the same equations above but we add two constraints. First, the total weight should be zero and second, we need to constraint our returns to 0.1%.

Hedge Fund Portfolios (Total Weights = 0)

Hedge Fund Portfolio-1

(13)

(14)

Here we construct a minimum variance portfolio for each of the 100 stocks in the S&P 100 index and assign the minimum variance portfolio weight to be 1. As we know the sum of all weights of all the companies in an index is 1. Hence the resulting total index weight is 1. So the total portfolio weight will be one minus one which is zero. So we have equal long/short positions. We can say here that our beta is close to zero.

Hedge Fund Portfolio-2

(15)

(16)

This portfolio mainly is based on three important factors. Those are minimum variance, Index and cap weight. And the important part about this portfolio is that we take minimum total weights of variance portfolio as 0. We then calculate the cap weight for all the stocks with respect to the S&P 100 index. Then we add the cap weight to the above formula for each stock and find out the resulting weight of each stock. Adding them all up we find the total portfolio weight. Also, here we have equal long/short positions and our beta is close to zero.

General Long-Short Portfolios (Total Weights = 1)

General Portfolio-1

(17)

(18)

The important part about this portfolio is that we take the total weight of the portfolio as one in this strategy. We construct a minimum variance portfolio for each of the stocks in the S&P 100 index and we assign the minimum variance portfolio weight to be 0. So the total portfolio weight will be zero plus one which is one. Here we have the prime portfolio as the Index and the Min Variance portfolio as an overlay which emphasizes whatever we think will give us a good return. We invest 100% of our wealth in long positions so we have long-short = 1.

General Portfolio-2

(19)

This portfolio mainly is based on three important factors. Those are minimum variance, Index and cap weight. And the important part about this portfolio is that we take minimum variance portfolio total weight as 1. We then calculate the cap weight for all the stocks with respect to the S&P 100 index. Then we add the cap weight to the above formula for each stock and find out the resulting weight of each stock. Adding them all up we find the total portfolio weight. Here our base portfolio is the minimum variance portfolio and the (Cap-Index) acts as an overlay. We invest 100% of our wealth in long positions so we have long-short = 1.

In general, in all of these portfolios we assume that whatever we make from the short sale we reinvest it in the long position.

3. Results

After looking into some papers relevant to our topic of research we came up with few new strategies to construct our portfolios. To test their performance using past market data for a specific intervals of time, we tested the performance of our portfolios for two different intervals of time. The first test was done from 2011-2013 and after that we performed a stress test on our portfolios that was from 2007-2008. We did the stress test on our portfolios in order to test their robustness. These back tests helped us to determine which portfolio made the highest return during the period of 2011-2013 and which portfolio survived in the crisis of 2007-2008. We are not taking into account the transaction cost and managerial fees.

This is our wealth equation which we used to back test the portfolios by monthly rebalancing the portfolios. We start by buying and short selling the stocks using the first day prices then we liquidate the portfolio by the end of each month, we reinvest the returns in the following month’s portfolio till the end of the period specified .

(20)

where

W is the wealth the investor owns,

Δ is the number of stocks,

S is the stock price.

Figure 1 shows the returns for S&P 100 from 2011-2013. We can see it makes a profit of 45.5752% cumulative over three years. The graph shows the monthly performance of S&P 100.

Figure 2 shows the performance of the four portfolios that we created against the S&P 100 from 2011-13. Hedge Fund Portfolios (Total Weights = 0)

Hedge Fund Portfolio-1

The table shows above our returns of portfolio-1 for 2011-2013. Portfolio-1 was our first back test in 2011 it gave good returns but by the end of 2013 it made only 32% cumulative in three years which was less than S&P 100 returns.

Hedge Fund Portfolio-2

Above are the returns for our portfolio-4 for 2011-2013 we can see that our portfolio made loss at the beginning of 2011 but in 2012-2013 it was making profit and we ended up with 42.32% cumulative profit over three years which was under performing the S&P 100 index by about 3%.

General Long-Short Portfolios (Total Weights = 1)

General Portfolio-1

Above are the returns for our portfolio-2 for 2011-2013, we can see that our portfolio made loss in 2011 but in 2012-2013 it was making profit and we ended up with 61.54% cumulative profit over three years which was outperforming the S&P 100 index by about 16%.

General Portfolio-2

Above are the returns for our portfolio 3 for 2011-2013, we can see that our portfolio made profit through 2011-2013 and we ended up with 75.99% cumulative profit over three years which was outperforming the S&P 100 index by about 30%.

Figure 3 shows the returns for S&P 100 from 2007-2008. We can see it made a loss of 34.6557% cumulative over two years. The graph shows the monthly performance of S&P 100 during crisis.

Figure 4 shows the performance of the four portfolios that we created against the S&P 100 from 2007-2008.

Hedge Fund Portfolios (Total Weights = 0)

Hedge Fund Portfolio-1 (Stress Test)

Above are the returns for our portfolio-1 for 2007-2008, we can see that our portfolio was performing well in 2007 but it made a huge loss at the beginning of 2008 and we ended up with 51% loss which was more loss than the market made.

Hedge Fund Portfolio-2 (Stress Test)

Above are the returns for our portfolio-4 for 2007-2008, we can see that our portfolio was performing well in 2007 but it made a profit in 2008 and we ended up with 3% profit which was better than the market. And this was the only portfolio that made profit during the stress test.

General Long-Short Portfolios (Total Weights = 1)

General Portfolio-1 (Stress Test)

Above are the returns for our portfolio 2 for 2007-2008, we can see that our portfolio was performing well in 2007 but it made a loss in 2008 and we ended up with 25% loss which was better than the market.

General Portfolio-2 (Stress Test)

Above are the returns for our portfolio 3 for 2007-2008 we can see that our portfolio was performing well in 2007 but it made a huge loss in the beginning of 2008 and we ended up with 70% loss which was more loss than the market made.

4. Conclusions

We managed to implement four portfolios using the smart beta strategies. Although smart beta has many definitions, our definition is that smart beta is a portfolio management strategy involving (Minimum Variance, Cap Weight, Economic Scale) in which we combine them and create beta dynamic portfolios. According to the article “Is Smart Beta really Smart?” [2] , smart beta strategies flunk the stress tests as shown in Figure 4. But we managed to create hedge fund portfolio-2 which was stable under stress. Our hedge fund portfolios can be used by an investor who is risk averse and our general portfolios in Figure 2 can be used to obtain higher returns. Looking back at the four portfolios, we can say that our beta is smart because it is a dynamic beta which adapts to the market movements [9] .

The tables below provide the properties about each portfolio during the different time periods of the back test.

Back Test (2011-2013)

Stress Test (2007-2008)

Acknowledgements

I would like to thank my adviser Professor David Starer and Professor Ionut Florescu for their help and advice during this research. I would like to thank the chairman of Anasser Group Eng. Faisal Al Mahdi for his support.

References