Journal of Mathematical Finance
Vol.3 No.1(2013), Article ID:28399,8 pages DOI:10.4236/jmf.2013.31012
Optimal Portfolio Strategy with Discounted Stochastic Cash Inflows
Department of Mathematics, Faculty of Physical Sciences, University of Benin, Benin City, Nigeria
Email: nkekicharles2003@yahoo.com
Received March 19, 2012; revised June 10, 2012; accepted June 25, 2012
Keywords: Optimal Portfolio; Stochastic Cash Inflows; Inflation-Linked Bond; Variational Form; Intertemporal Hedging Terms
ABSTRACT
This paper examines optimal portfolios with discounted stochastic cash inflows (SCI). The cash inflows are invested into a market that is characterized by inflation-linked bond, a stock and a cash account. It was assumed that inflationlinked bond, stock and the cash inflows are stochastic and follow a standard geometric Brownian motion. The variational form of Merton portfolio strategy was obtained by assuming that the investor chooses constant relative risk averse (CRRA) utility function. The inter-temporal hedging terms that offset any shock to the SCI were obtained. A closed form solution to our resulting non-linear partial differential equation was obtained.
1. Introduction
This paper consider the optimal portfolio strategies with valuing expected discounted cash inflows. It was assumed that the underlying assets and cash inflow process follow a standard geometric Brownian motion. The investment of the investor’s SCI into a cash account, an inflationlinked bond and a stock was considered. The SCI and stock price were correlated with inflation and stock market risk.
In a related literature, [1] studied an optimal investment problem in a continuous-time framework where the interest rate follows the Cox-Ingersoll-Ross dynamics. They obtained a closed form solution for the optimal investment strategy under a complete market framework. They assumed that the investor chooses CRRA utility function. [2] considered the process of finding the optimal portfolio, optimal consumption and the efficient frontier for a small agent in an economy. They also considered financial market that composed of two sources of uncertainties: an m-dimensional Brownian motion and a continuous time Markov chain. They found theoretically, that the regimes of an economy have a significant impacts on the portfolio and consumption decision as well as on the efficient frontier of a small investor. [3] studied the present value and overcome the difficulty of independence by reversing the order of the cash flow. He found that similar recursive formulas for the present value is also applicable to the future value of the expected returns. [4] considered the problem of constructing a portfolio of finitely many assets whose returns are described by a discrete joint distribution. They proposed a new portfolio optimization model involving stochastic dominance constraints on the portfolio return. [5] studied how portfolio composition changes with individual wealth. [6] considered the present value of expected future contribution into the pension fund. [7] investigated the stochastic dynamics of depository financial institution assets, liabilities and capital under the influence of macroeconomic factors. They adopted dynamic programming techniques in their optimization process. They provided an analysis of the economic aspects of the depository financial institution modeling. [8] studied a portfolio problem of a fund manager who wants to maximize the expected utility of his terminal wealth in a complete financial market. He found that the optimal portfolio is formed by three components: a speculative, an hedging, and a preference-free hedging component. He obtained a close form solution to the asset allocation problem. [9] considered the optimal portfolio selection problem with portfolio constraints. They derived the general utility function using the martingale approach. They found that using CRRA utility function, optimal policies can be obtained explicitly when there are minimum capital requirements. ([10,11]) studied the optimal portfolio management in the accumulation phase of a defined contribution pension scheme. They obtained portfolio values with hedging strategies for a pension plan member. In this paper, we consider the optimal portfolio and investment strategies involving cash inflow valuation over time. We obtain explicitly, analytical solution to our resulting HJB equation. The risk-free rate is assume to be deterministic.
The remaining parts of the paper is structured as follows: In Section 2, we described the structure of the financial market; In Section 3, we consider the dynamics of the discounted present value of expected SCI process; In Section 4, we consider the wealth process of the investor; In Section 5, we consider the valuation of the discounted present value of expected SCI process of the investor as well as the sensitivity of the present value of the SCI; In Section 6, we consider the optimization program and optimal portfolio and optimal solution of the investor’s wealth using CRRA utility function; Section 7 concludes the paper.
2. The Model
Let  be a probability space. Let
be a probability space. Let
 , where
, where
 . The Brownian motions
. The Brownian motions
 is a 2-dimensional process, defined on a given filtered probability space
is a 2-dimensional process, defined on a given filtered probability space
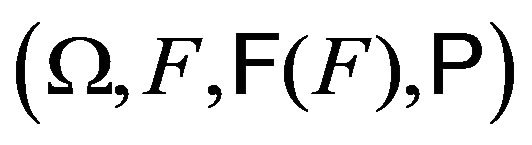 ,
,  , where
, where  is the real world probability measure,
is the real world probability measure,  the time period,
the time period,  the terminal time period,
the terminal time period,  is the Brownian motion with respect to source of uncertainty arising from inflation and
is the Brownian motion with respect to source of uncertainty arising from inflation and  is the Brownian motion with respect to source of uncertainty arising from the stock market. It is assumed that the market is arbitrage-free, complete and continuously open between time period
is the Brownian motion with respect to source of uncertainty arising from the stock market. It is assumed that the market is arbitrage-free, complete and continuously open between time period  and
and .
.
Financial Model
The dynamics for the cash account with the price  at time
at time  is given by
is given by
 (1)
(1)
where  is the short term interest rate. The stock price
is the short term interest rate. The stock price  at time
at time  is given by the dynamics:
is given by the dynamics:
 (2)
(2)
where, 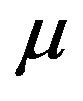 is the expected growth rate of stock price,
is the expected growth rate of stock price,
 and
and 
 is the volatility of stock. The price of the inflation-linked bond
is the volatility of stock. The price of the inflation-linked bond  is given by the dynamics:
is given by the dynamics:
 (3)
(3)
where,  is the volatility of inflation-linked bond,
is the volatility of inflation-linked bond,  is the market price of inflation risk,
is the market price of inflation risk,  is the inflation index at time
is the inflation index at time  and has tha dynamics:
and has tha dynamics:

where  is the expected rate of inflation, which is the difference between nominal interest rate,
is the expected rate of inflation, which is the difference between nominal interest rate,  real interest rate
real interest rate  and
and  is the volatility of inflation index. Since the market is complete, we have that
is the volatility of inflation index. Since the market is complete, we have that
 (4)
(4)
 (5)
(5)
Therefore, the market price of market risk is given by
 (6)
(6)
where,  is the market price of stock market risk. The exponential process
is the market price of stock market risk. The exponential process
 is assumed to be a martingale. We now define the state-price density function by
is assumed to be a martingale. We now define the state-price density function by

3. Dynamics of Stochastic Cash Inflows
The dynamics of the stochastic cash inflows with price process,  is given by
is given by
 (7)
(7)
where,  is the volatility of the cash inflows and
is the volatility of the cash inflows and  is the expected growth rate of the cash inflows.
is the expected growth rate of the cash inflows.  is the volatility arising from inflation and
is the volatility arising from inflation and  is the volatility arising from the stock market. Figure 1 presents the simulated diffusion paths of (7).
is the volatility arising from the stock market. Figure 1 presents the simulated diffusion paths of (7).
Figure 1 was obtained by setting ,
,
 ,
,  ,
,  ,
,  ,
,  ,
,
 and
and .
.
Applying It lemma to (7), we obtain
lemma to (7), we obtain
 (8)
(8)

Figure 1. Simulated diffusion paths of the stochastic cash inflows.
4. The Wealth Process
Let  be the wealth process and
be the wealth process and
 be the portfolio value at time
be the portfolio value at time where
where  is the portfolio value in inflation-linked bond and
is the portfolio value in inflation-linked bond and  is the portfolio value in stock at time t. Then,
is the portfolio value in stock at time t. Then,  is the portfolio value in cash account at time
is the portfolio value in cash account at time . Therefore, the dynamics of the wealth process is given by
. Therefore, the dynamics of the wealth process is given by
 (9)
(9)
Substituting (1), (2) and (3) into (9), we obtain
 (10)
(10)
5. The Discounted Value of SCI
In this section, we determine the value of expected discounted SCI.
Definition 1:
The discounted value of the expected future SCI is defined as
 (11)
(11)
where,  is the conditional expectation with respect to the Brownian filtration
is the conditional expectation with respect to the Brownian filtration  and
and
 is the stochastic discount factor which adjusts for nominal interest rate and market price of risks for stock and inflation-linked bond.
is the stochastic discount factor which adjusts for nominal interest rate and market price of risks for stock and inflation-linked bond.
Proposition 1:
Suppose  is the discounted value of the expected future SCI, then
is the discounted value of the expected future SCI, then
 (12)
(12)
Proof. By definition 1, we have that
 (13)
(13)
Applying change of variable on (13), we have
 (14)
(14)
Applying parallelogram law and martingale principles on (14), we have

Therefore,
 (15)
(15)
Integrating, we have
 (16)
(16)
Figure 2 was obtained by setting , k = 0.099, r = 0.04,
, k = 0.099, r = 0.04,  ,
,  ,
, 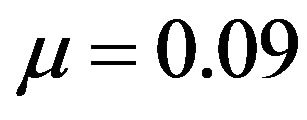 ,
,  ,
,  ,
,  and
and .
.
At , we obtain the present discounted value of future SCI to be
, we obtain the present discounted value of future SCI to be
 (17)
(17)
If  and we allow
and we allow  i.e.,
i.e.,
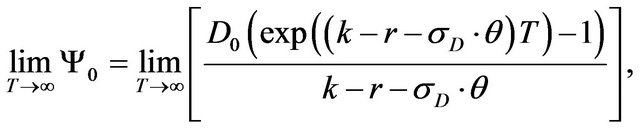

For a deterministic case, we have the present discounted value future deterministic cash inflows to be

Figure 2. The flow of the discounted value of SCI.
 (18)
(18)
Hence,

This shows that as ,
,  converges to
converges to
 , provided
, provided .
.
For the deterministic case, it shows that as ,
,
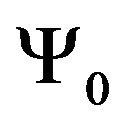 converges to
converges to , provided
, provided .
.
Figure 3 was obtained by setting , k = 0.099, r = 0.04,
, k = 0.099, r = 0.04,  ,
,  ,
,  ,
,  ,
,  ,
,  and
and .
.
Figure 2 represents the flow of the discounted value of stochastic cash inflow in the investment at time  and Figure 3 represents the present value of discounted future SCI at time
and Figure 3 represents the present value of discounted future SCI at time 
We now consider the sensitivity analysis of  Proposition 2 establishes this fact.
Proposition 2 establishes this fact.
Proposition 2:
Let , then
, then

Proof. The results follow by taking the partial derivatives of  with respect to
with respect to ,
,  ,
,  ,
,  and
and , respectively.
, respectively.


Figure 3. The present discounted value of future SCI.


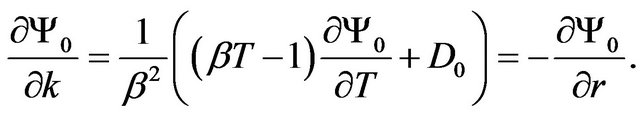
Table 1 shows the sensitivity analysis of the discounted value of the SCI.
Proposition 3:
Suppose that Proposition 1 holds, then
 (19)
(19)
Proof. Finding the differential of both sides of (16) and then substitute (7), we have

Let  be a value process at time
be a value process at time . We defined
. We defined
Table 1. Simulation of the sensitivity analysis.

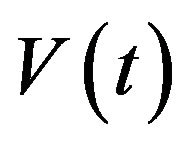 as
as
 (20)
(20)
where,  satisfy (10) and
satisfy (10) and  satisfy (19).
satisfy (19).
Proposition 4:
Let  satisfy (20),
satisfy (20),  satisfy (10) and
satisfy (10) and  satisfy (19), then
satisfy (19), then
 (21)
(21)
Proof. Finding the differential of both sides of (20) and then substitute in (10) and (19), the result follows.
6. Optimization of the Value of Wealth Process
We define the general value function

where  is the path of
is the path of . Define
. Define  to be the set of all admissible portfolio strategy that are F-progressively measurable, that satisfy the integrability conditions
to be the set of all admissible portfolio strategy that are F-progressively measurable, that satisfy the integrability conditions  and let
and let  be a concave function in
be a concave function in  such that
such that  satisfies the HJB equation
satisfies the HJB equation

Therefore, by applying Itô lemma on (21), we obtain the following HJB equation:
 (22)
(22)
subject to:

where,

(23)
Let  be the solution of the HJB equation (22). Since the utility function is concave and the value function is smooth, i.e.,
be the solution of the HJB equation (22). Since the utility function is concave and the value function is smooth, i.e., 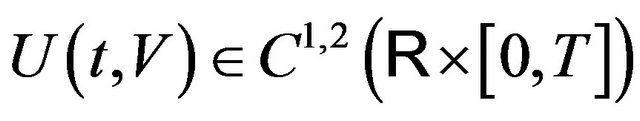 , then (22) is well-defined. Hence, we have the following:
, then (22) is well-defined. Hence, we have the following:
 (24)
(24)
from (24), we have
 (25)
(25)
Substituting (25) into (22), we obtain the following HJB equation:
 (26)
(26)
This is the resulting HJB equation of our problem.
Proposition 5:
The solution of the HJB equation (26) is of the form

with
 (27)
(27)
Proof. Finding the partial derivatives of
 with respect to
with respect to ,
,  ,
,  ,
,  ,
,
 and
and  and then substitute into (26), we obtain the following:
and then substitute into (26), we obtain the following:
 (28)
(28)
From (28), we obtain
 (29)
(29)
Using (29), we obtain
 (30)
(30)
Figure 4 was obtained by setting ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  and
and .
.
Figure 4 shows the expected value of utility of wealth at time  for different values of
for different values of . Here,
. Here,  measures the level of risk the investor is willing to take. Observe that the smaller the value of
measures the level of risk the investor is willing to take. Observe that the smaller the value of , the higher the expected value of wealth, and vice versa. Therefore, when
, the higher the expected value of wealth, and vice versa. Therefore, when , the expected value of utility of wealth,
, the expected value of utility of wealth,  , when
, when ,
,  , when
, when ,
,  and when
and when ,
, . Hence, the lower the rate at which investors are risk averse, the more the wealth that will accrue to them, and vice versa, which is an intuitive result.
. Hence, the lower the rate at which investors are risk averse, the more the wealth that will accrue to them, and vice versa, which is an intuitive result.
Proposition 6:
Suppose that  is the solution of the HJB Equation (26), then the optimal portfolio in inflationlinked bond, stock and cash account are given by
is the solution of the HJB Equation (26), then the optimal portfolio in inflationlinked bond, stock and cash account are given by
 (31)
(31)

Figure 4. The expected value of utility of wealth for different values of γ.
 (32)
(32)

Proof. From (25), we have that

But,


Therefore,

It implies that
 (33)
(33)
 (34)
(34)

(35)
From (33), the first term represents the classical portfolio strategy while the second term represents the intertemporal hedging strategy that offset any shock to the SCI at time t. From (34),
 represents the classical portfolio strategy at time
represents the classical portfolio strategy at time  and
and
 represents the intertemporal hedging term that offset shock resulting from the SCI at time
represents the intertemporal hedging term that offset shock resulting from the SCI at time . From (35), observe that these hedging terms can be transfer to cash account at time
. From (35), observe that these hedging terms can be transfer to cash account at time  or it can be reinvest in stock and in inflation-linked bond at time
or it can be reinvest in stock and in inflation-linked bond at time .
.
Figure 5 was obtained by setting ,
,  ,
,  ,
,  ,
,  ,
, ,
,  ,
,  ,
,  ,
,  ,
,  and
and . The optimal portfolio value in inflation-linked bond at time
. The optimal portfolio value in inflation-linked bond at time  is obtained as 0.16 (or 16%).
is obtained as 0.16 (or 16%).
Figure 6 was obtained by setting ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  and
and . The optimal portfolio value in stock at time
. The optimal portfolio value in stock at time  is obtained as 1.001562 (or 100.1562%).
is obtained as 1.001562 (or 100.1562%).
|
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  and
and . The optimal portfolio value in cash account at time
. The optimal portfolio value in cash account at time  is obtained as −0.161562 (or −16.1562%).
is obtained as −0.161562 (or −16.1562%). In Figures 5-7, we set ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  and
and . Figure 5 shows the portfolio value in inflation-linked bond. We found that the optimal portfolio value in inflation-linked bond at time
. Figure 5 shows the portfolio value in inflation-linked bond. We found that the optimal portfolio value in inflation-linked bond at time  is 0.16 (or 16%). Figure 6 shows the portfolio value in stock. We found that the optimal portfolio value in stock at time
is 0.16 (or 16%). Figure 6 shows the portfolio value in stock. We found that the optimal portfolio value in stock at time  is 1.001562 (or 100.1562%). Figure 7 shows the portfolio value in cash
is 1.001562 (or 100.1562%). Figure 7 shows the portfolio value in cash

Figure 5. Portfolio value in inflation-linked bond.

Figure 6. Portfolio value in stock.

Figure 7. Portfolio value in cash account.
account. We found that the optimal portfolio value in cash account at time t = 10 is −0.161562 (or −16.1562%).
7. Conclusion
The optimal portfolio strategy X with discounted stochastic cash inflows was considered. It was assumed that the cash inflow, stock and inflation-linked bond are stochastic and follow a standard geometric Brownian motion. The sensitivity analysis of the present value of the discounted cash inflows was carried out in this paper and the results are presented in Table 1. Analytical solution to the resulting HJB equation was obtained. It was found that the smaller the value of  (which measure the level of risk the investor is willing to take), the higher the expected value of wealth, and vice versa. The optimal portfolio values in stock, inflation-linked bond and cash account were obtained. The resulting optimal portfolio values in stock and inflation-linked bond were found to involve intertemporal hedging terms that offset any shock to the SCI.
(which measure the level of risk the investor is willing to take), the higher the expected value of wealth, and vice versa. The optimal portfolio values in stock, inflation-linked bond and cash account were obtained. The resulting optimal portfolio values in stock and inflation-linked bond were found to involve intertemporal hedging terms that offset any shock to the SCI.
REFERENCES
- G. Deelstra, M. Grasselli and P. Koehl, “Optimal Investment Strategies in a CIR Framework,” Journal of Applied Probability, Vol. 37, No. 4, 2000, pp. 936-946. doi:10.1239/jap/1014843074
- D. O. Cajueiro and T. Yoneyama, “Optimal Portfolio, Optimal Consumption and the Markowitz Mean-Variance Analysis in a Switching Diffusion Market,” 2003. unb.br/face/eco/seminarios/sem0803.pdf
- A. Zaks, “Present Value of Annuities under Random Rates of Interest,” 2003. http://academic.research.microsoft.com/Publication/6244175/present-value-of-annuities-under-random-rates-of-interest
- D. Dentcheva and A. Ruszczynski, “Portfolio Optimization with Stochastic Dominance Constraints,” SIAM Journal on Optimization, Vol. 14, No. 2, 2003, pp. 548- 566. doi:10.1137/S1052623402420528
- D. Blake, “Efficiency, Risk Aversion and Portfolio Insurance: An Analysis of Financial Asset Portfolios Held by Investors in the United Kindom,” Economic Journal, Vol. 106, No. 438, 1996, pp. 1175-1192. doi:10.2307/2235514
- A. Zhang, “Stochastic Optimization in Finance and Life Insurance: Applications of the Martingale Method,” Ph.D. Thesis, University of Kaiserslauten, Kaiserslautern, 2007.
- J. Mukuddem-Peterson, M. A. Peterson and I. M. Schoeman, “An Application of Stochastic Optimization Theory to Institutional Finance,” Applied Mathematics Sciences, Vol. 1, No. 28, 2007, pp. 1359-1385.
- P. Battocchio, “Optimal Portfolio Strategies with Stochastic Wage Income: The Case of a Defined Contribution Pension Plan,” Working Paper, Université Catholique de Louvain, Louvain-la-Neuve, 2002.
- B. H. Lim and U. J. Choi, “Optimal Consumption and Portfolio Selection with Portfolio Constraints,” International Sciences, Vol. 4, 2009, pp. 293-309.
- C. I. Nkeki, “On Optimal Portfolio Management of the Accumulation Phase of a Defined Contributory Pension Scheme,” Ph.D. Thesis, University of Ibadan, Ibadan, 2011.
- C. I. Nkeki and C. R. Nwozo, “Variational Form of Classical Portfolio Strategy and Expected Wealth for a Defined Contributory Pension Scheme,” Journal of Mathematical Finance, Vol. 2, No. 1, 2012, pp. 132-139. doi:10.4236/jmf.2012.21015

