ABSTRACT

In this paper, we consider simulated minimum Hellinger distance (SMHD) inferences for count data. We consider grouped and ungrouped data and emphasize SMHD methods. The approaches extend the methods based on the deterministic version of Hellinger distance for count data. The methods are general, it only requires that random samples from the discrete parametric family can be drawn and can be used as alternative methods to estimation using probability generating function (pgf) or methods based matching moments. Whereas this paper focuses on count data, goodness of fit tests based on simulated Hellinger distance can also be applied for testing goodness of fit for continuous distributions when continuous observations are grouped into intervals like in the case of the traditional Pearson’s statistics. Asymptotic properties of the SMHD methods are studied and the methods appear to preserve the properties of having good efficiency and robustness of the deterministic version.

Keywords:

break Down Points, Robustness, Power Mixture, Esscher Transform, Mixture Discrete Distributions, Chi-Square Tests Statistics

1. Introduction

1.1. New Distribution Created Using Probability Generating Functions

Nonnegative discrete parametric families of distributions are useful for modeling count data. Many of these families do not have closed form probability mass functions nor closed form formulas to express the probability mass function (pmf) recursively. Their pmfs can only be expressed using an infinite series representation but their corresponding Laplace transforms have a closed form and, in many situations, they are relatively simple. Probability generating functions are often used for discrete distributions but Laplace transforms are equivalent and can also be used. In this paper, we use Laplace transforms but they will be converted to probability generating functions (pgfs) whenever the need arises to link with results which already appear in the literature. We begin with a few examples to illustrate the situation often encountered when new distributions are created.

Example 1 (Discrete stable distributions) The random variable $X\ge 0$ follows a positive stable law if the probability generating function and Laplace transform are given respectively as

$P_{\beta }\left(s\right)=E\left(s^X\right)={\text{e}}^{-\lambda {\left(1-s\right)}^{\alpha }},0<\alpha \le 1,\lambda >0,\beta ={\left(\lambda ,\alpha \right)}^{\prime },\left|s\right|\le 1$

and

${\phi }_{\beta }\left(s\right)=E\left({\text{e}}^{-sX}\right)={\text{e}}^{-\lambda {\left(1-{\text{e}}^{-s}\right)}^{\alpha }},0<\alpha \le 1,\lambda >0,\beta ={\left(\lambda ,\alpha \right)}^{\prime },s\ge 0$ .

The distribution was introduced by Christoph and Schreiber [1] .

It is easy to see that ${\phi }_{\beta }\left(s\right)=P_{\beta }\left({\text{e}}^{-s}\right)$ .

The Poisson distribution can be obtained by fixing $\alpha =1$ . The distribution is infinitely divisible and displays long tail behavior. The recursive formula for its mass function has been obtained; see expression (8) given by Christoph and Schreiber [1] .

Now if we allow $\lambda$ to be a random variable with an inverse Gaussian distribution whose Laplace transform is given by $h\left(s\right)={\text{e}}^{\mu \left(1-\sqrt{1+\frac{2}{\mu }s}\right)},s\ge -\frac{\mu }{2}$ , a mixed

nonnegative discrete stable distribution can be created with Laplace transform given by

${\phi }_{\beta }\left(s\right)={\displaystyle {\int }_0^{\infty }{\left(g\left(s\right)\right)}^{\lambda }\text{d}H\left(\lambda \right)}$ ,

where $g\left(s\right)={\text{e}}^{-{\left(1-s\right)}^{\alpha }}$ and $H\left(\lambda \right)$ is the distribution with Laplace transform $h\left(s\right)$ . The resulting Laplace transform,

${\phi }_{\beta }\left(s\right)=\exp \left(\mu \left(1-\sqrt{1+\frac{2}{\mu }{\left(1-{\text{e}}^{-s}\right)}^{\alpha }}\right)\right)$ ,

is the Laplace transform of a nonnegative infinitely divisible (ID) distribution.

We can see that it is not always straightforward to find the recursive formula for the pmf for a nonnegative count distribution. Even if it is available, it might still complicated to be used numerically for inferences meanwhile the Laplace transform or pgf can have a relatively simple representation.

We can observe that the new distribution is obtained by using the inverse Gaussian distribution as a mixing distribution. This is also an example of the use of a power mixture (PM) operator to obtain a new distribution. The PM operator will be further discussed in Section 1.2.

From a statistical point of view, when neither a closed form pmf nor a recursive formula for the pmf exists, maximum likelihood estimation can be difficult to implement.

The power mixture operator was introduced by Abate and Whitt [2] (1996) as a way to create new distributions from an infinitely divisible (ID) distribution together with a mixing distribution using Laplace transforms (LT). We shall review it here in the next section, after a definition of an ID distribution.

Definition 1.1.3. A nonnegative random variable X is infinitely divisible if its Laplace transform can be written as

$\psi \left(s\right)={\left(k_n\left(s\right)\right)}^n,n=1,2,\cdots$ ,

where $k_n\left(s\right)$ also is the Laplace transform of a random variable. In many situations, $k_n\left(s\right)$ and $\psi \left(s\right)$ belong to the same parametric family. See Panjer and Willmott [3] (1992, p42) for this definition.

Abate and Whitt [2] (1996) introduced the power mixture (PM) operator for ID distributions and also some other operators. To the operators already developed by them, we add the Esscher transform operator and the shift operator. All operators considered are discussed below.

1.2. Operational calculus on Laplace Transforms

1.2.1. Power Mixture (PM) Operator

Suppose that $X_t$ is an infinitely divisible nonnegative discrete random variable such that the Laplace transform can be expressed as ${\left(\kappa \left(s\right)\right)}^t,t\ge 0$ , where $\kappa \left(s\right)$ is the Laplace transform of X, which is nonnegative and infinitely divisible as well. The power mixture (PM) with mixing distribution function $H\left(y\right)$ and Laplace transform ${\kappa }_H\left(s\right)$ of a nonnegative random variable Y is defined as the Laplace transform

$\eta \left(s\right)=\text{PM}\left(\kappa ,H\right)={\displaystyle {\int }_0^{\infty }{\left(\kappa \left(s\right)\right)}^t\text{d}H\left(t\right)}={\kappa }_H\left(-\log \left(\kappa \left(s\right)\right)\right)$ .

Furthermore, if $H\left(y\right)$ is infinitely divisible, then the distribution with Laplace transform $\eta \left(s\right)$ is also infinitely divisible. The random variable $Y\ge 0$ with distribution $H\left(y\right)$ can be discrete or continuous but needs to be ID. This is the PM method for creating new parametric families, i.e., using the PM operator. The PM method can be viewed as a form of continuous compounding method. The ID property can be dropped but as a result the new distribution created using the PM operator needs not be ID. For the traditional compounding methods, see Klugman et al. [4] (p141-148). Abate and Whitt [2] also mentioned other methods.

Example 2 (Generalized negative binomial) The generalized negative binomial (GNB) distribution introduced by Gerber [5] can be viewed as a power variance function distribution mixture of a Poisson distribution. The power variance function distribution introduced by Hougaard [6] is obtained by tilting the positive stable distribution using a parameter $\theta$ . It is a three-parameter continuous nonnegative distribution with Laplace transform given by

${\kappa }_H\left(s\right)=\exp \left\{-\lambda {\left(\theta +s\right)}^{\alpha }-{\theta }^{\alpha }\right\},\lambda ,\theta >0,0<\alpha <1$ .

Gerber [5] used a different parameterization and named this distribution generalized gamma. It is also called positive tempered stable distribution in finance.

Let $\kappa \left(s\right)={\text{e}}^{\left({\text{e}}^{-s}-1\right)}$ be the Laplace transform of a Poisson distribution with rate $\mu =1$ . The Laplace transform of the GNB distribution can be represented as

$\eta \left(s\right)=\exp \left(-\lambda {\left(\theta -{\text{e}}^{-s}+1\right)}^{\alpha }-{\theta }^{\alpha }\right)$ .

The corresponding pgf can be expressed as

$P\left(s\right)=\exp \left(-\lambda {\left(\theta -s+1\right)}^{\alpha }-{\theta }^{\alpha }\right)$ .

The pgf is given by expression (21) in the paper by Gerber [5] . The GNB distribution is infinitely divisible. If stochastic processes are used instead of distributions, the distribution can also be derived from a stochastic process point of view by considering a Poisson process subordinated to a generalized gamma process and obtain the new distribution as the distribution of increments of the new process created. See section 6 of Abate and Whitt [2] (p92-93). See Zhu and Joe [7] for other distributions which are related to the GNB distribution.

Note that, if $H\left(y\right)$ is discrete, $\eta \left(s\right)$ is the Laplace transform of a random variable expressible as a random sum. A random sum is also called stopped sum in the literature, see chapter 9 by Johnson et al. [8] (p343-403). The Neymann-Type A distribution given below is an example of a distribution of a random sum.

Example 3 Let $X={\displaystyle {\sum }_{i=1}^Y{U}_i}$ ,the $U_i$ ’s conditioning on Y are independent and identically distributed and follows a Poisson distribution with rate $ф$ and Y is distributed with a Poisson distribution with rate $\lambda$ . Using the Power mixture operator we conclude that the LT for X is

$\eta \left(s\right)=\exp \left(\lambda \left({\text{e}}^{ф\left({\text{e}}^{-s}-1\right)}-1\right)\right)$ ,

and the pgf is

$P\left(s\right)=\exp \left(\lambda \left({\text{e}}^{ф\left(s-1\right)}-1\right)\right)$ .

Properties and applications of the Neymann type A distribution have been studied by Johnson et al. [8] (p368-378). The mean and variance of X are given respectively by $E\left(X\right)=\lambda ф$ and $V\left(X\right)=\lambda ф\left(1+ф\right)$ . From these expressions, moment estimators (MM) have closed form expressions, see section (4.1) for comparisons between MM estimators and SMHD estimators in a numerical study. For applications often the parameter $\lambda$ is smaller than the parameter $ф$ .

1.2.2. Esscher transform operator

By tilting the density function using the Esscher transform, the Esscher transform operator can be defined and, provided the tilting parameter $\tau$ introduced is identifiable, new distributions can be created from existing ones.

Let X be the original random variable with Laplace transform $\kappa \left(s\right)$ . The Esscher transform operator which can be viewed as a tilting operator is defined as

$\eta \left(s\right)=\text{Esscher}\left(\kappa ,\tau \right)=\frac{\kappa \left(s+\tau \right)}{\kappa \left(\tau \right)}$ .

1.2.3. Shift operator

Let $\kappa \left(s\right)$ be the Laplace transform of a positive continuous random variable X. The Laplace transform of $Y=X-\tau ,Y\ge \tau \ge 0$ is given by ${\text{e}}^{\tau }\kappa \left(s\right)$ . So, we can define the shift operator as

$\eta \left(s\right)=\text{Shift}\left(\kappa ,\tau \right)={\text{e}}^{\tau }\kappa \left(s\right)$ .

In some cases, even the pmf of Y has a closed form but the maximum likelihood (ML) estimators might be attained at the boundaries, the ML estimators might not have the regular optimum properties.

Note that parallel to the closed form pgf expressions for these new discrete distributions, it is often simple to simulate from the new distributions if we can simulate from the original distribution before the operators are applied. For example, let us consider the new distribution obtained by using the Esscher operator. It suffices to simulate from the distribution before applying the operator and apply the acceptance-rejection method to obtain a sample from the Esscher transformed distribution. The situation is similar for new distributions created by the PM operator. If we can simulate one observation from the mixing distribution of Y which gives a realized value t and if it is not difficult to draw one observation from the distribution with LT $\kappa {\left(s\right)}^t$ then combining these two steps, we would be able to obtain one observation from the new distribution created by the PM operator. Consequently, simulated methods of inferences offer alternative methods to inferences methods based on matching selected points of the empirical pgf with its model counterpart or other related methods, see Doray et al. [9] for regression methods using selected points of the pgfs. For these methods there is some arbitrariness on the choice of points which make it difficult to apply. The techniques of using a continuum number of points to match are more involved numerically, see Carrasco and Florens [10] . The new methods also avoid the arbitrariness of the choice of points which is needed for the regression methods and the k-L procedures as proposed by Feurverger and McDunnough [11] if characteristic functions are used instead of probability generating functions and they are more robust than methods based on matching moments (MM) in general. We can reach the same conclusions for another class of distributions namely mixture distributions created by other mixing mechanisms, see Klugman et al. [4] , Nadarajah and Kotz [12] , Nadarajah and Kotz [13] . These distributions might not display closed form pmf or the pmf are only expressible only using special functions such as the confluent hypergeometric functions. For these models, likelihood methods might also be difficult to implement.

This leads us to look for alternative methods such as the simulated minimum Hellinger distance (SMHD) methods for count data. We shall consider grouped count data and ungrouped count data. With grouped data, it leads to simulated chi-square type statistics which can be used for model testing for discrete or continuous models. These statistics are similar to the traditional Pearson statistics. For model testing with continuous distributions, continuous observations when grouped into intervals are reduced to count data and we do not need to integrate the model density functions on intervals using SMHD methods, it suffices to simulate from the continuous model and construct sample distribution functions to obtain estimate interval probabilities. Therefore, the scopes of applications of simulated methods are widened due to these features.

We briefly describe the classical minimum Hellinger distance methods introduced by Simpson [14] , Simpson [15] for estimation for count data in the next section and we shall develop inference methods based on a simulated version of this HD distance following Pakes and Pollard [16] (1989), who have developed an elegant asymptotic theory for estimators obtained by minimizing a simulated objective function expressible as the Euclidean norm of a random vector of functions. As an example, they have shown that the simulated minimum chi-square estimators without weight satisfy the regularity conditions for being consistent and have an asymptotic normal distribution, see Pakes and Pollard [16] (p1048). They work with properties of some special classes of sets to check the regularity conditions of their Theorem 3.3. Meanwhile, Newey and McFadden [17] (p2187) work with properties of random functions and introduce a stochastic version of the classical equicontinuity property of real analysis. In this paper, we shall also extend the notion of continuity of real analysis to a version which only holds in probability for random functions which we call continuity in probability for a sequence of random functions which is similar to the notion of continuity with probability one as discussed by Newey and McFadden [17] (p2132) in their Theorem 2.6. We also use the property of the compact domains under considerations shrink as the sample size $n\to \infty$ to verify conditions of Theorem 3.3 given by Pakes and Pollard [16] (1989) for SMHD methods using grouped data and conditions of Theorem 7.1 of Newey and McFadden [17] (p2185) for ungrouped data. This approach appears to be new and simpler that other approaches which have been used in the literature to establish asymptotic normality for estimators using simulations; previous approaches are very general but they are also more complicated to apply. A similar notion of continuity in probability has been introduced in the literature of stochastic processes.

It is worth to mention that simulated methods of inferences are relatively recent. In advanced econometrics textbook such as the book by Davidson and McKinnon [18] , only section 9.6 is devoted to simulated methods of inferences where the authors mention simulated methods of moments (MSM). The simulated version for HD methods will be referred to as version S and the original version which is deterministic will be referred to as version D in this paper. We briefly review the Hellinger distance and chi-square distance below and subsequently develop simulated inference methods for grouped and ungrouped count data using HD distance.

1.3. Hellinger and Chi-Square Distance Estimation

Assume that we have a random sample of n independent and identically distributed

(iid) nonnegative observations $X_1,\cdots ,X_n$ from a pmf $p_{\theta }\left(x\right)$ with $x=0,1,\cdots$ and

$\theta ={\left({\theta }_1,\cdots ,{\theta }_m\right)}^{\prime }$

is the vector of parameters of interest, ${\theta }_0$ is the vector of the true parameters. If the data are grouped into $r=k+1$ disjoint intervals 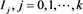so that they form a partition of the nonnegative real line, the unweighted chi-square distance is defined to be

,

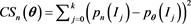where 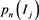is the proportion of the sample which fall into the interval 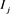and 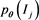is the probability of an observation which fall into 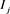under the pm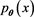f. If 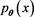has no closed form expression but we can draw a sample of size 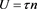from this distribution then clearly 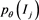can be estimated

by using the simulated sample of size U which is the proportion of observations of the simulated sample which has taken a value in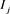. To illustrate their theory Pake and Pollard [16] (p1047-1048) considered simulated estimators obtained by minimizing with respect to 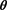the objective function

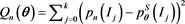
and show that the estimators satisfy the regularity conditions of their Theorem 3.1 and 3.3 which lead to conclude that the simulated estimators are consistent and have an asymptotic normal distribution. As we already know, a weighted version can be more efficient, if we attempt a version S for the Pearson’s chi square distance,

,

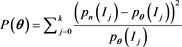and since the denominator of the summand involves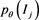, it is numerically not easy to introduce a version S. Clearly, if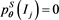, the version S of this

distance will run into numerical difficulties. The traditional and deterministic version of the Hellinger distance as given by

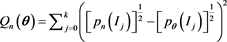(1)

is more appropriate for a version S and it is already known that it generates minimum HD estimators which are as efficient as the minimum chi-square estimators or maximum likelihood (ML) estimators for grouped data, see

Cressie-Read divergence measure with given by Cressie and Read [19] (p457) for version D.

Note that and by using Cauchy-Schwartz inequality, we have

,

so that and remains always bounded. Therefore the objective function for version S can be defined as

. (2)

Since the objective function remains bounded and this property continues to hold for the ungrouped data case, this suggests that SMHD methods could preserve some of the nice robustness properties of version D.

For ungrouped data, it is equivalent to have grouped data but using intervals with unit length and the number of classes is infinite, we shall develop SMHD estimation which is based on the objective function

. (3)

Note that for a data set the sum given by the RHS of the above expression only has a finite number of terms as when j is large.

The version D with

(4)

has been investigated by Simpson [14] , Simpson [15] who also shows that the MHD estimators have a high breakdown point of at least 50% and first order as efficient as the ML estimators. For the Poisson case, the ML estimator is the sample mean which has a zero breakdown point and consequently far less robust than the HD estimators, yet the HD estimators are first order as efficient as the ML estimators. This feature makes HD estimators attractive. For the notion of finite sample break down point as a measure of robustness, see Hogg et al. [20] (p594-595), Kloke and McKean [21] (p29) and for the notion of asymptotic breakdown point for large samples, see Maronna et al. [22] (p58).

Simpson [14] , Simpson [15] extended the works of Beran [23] for continuous distributions to discrete distributions. Beran [23] appears to be the first to introduce a weaker form of robustness not based on bounded influence function and shows that efficiency can be achieved for robust estimators not based on influence functions. Also, see Lindsay [24] for discussions on robustness of Hellinger distance estimators. Simulated versions extending some of the seminal works of Simpson will be introduced in this paper.

SMHD methods appear to be useful for actuarial studies when there is a need for fitting discrete risk models, see chapter 9 of Panjer and Willmott [3] (p292-238) for fitting discrete risk models using ML methods. The SMHD methods appear to be useful for other fields as well especially when there is a need to analyze count data with efficiency and robustness but the pmfs of the models do not have closed form expressions. For minimizing the objective functions to obtain SMHD estimators, simplex derivative free algorithm can be used and the R package already has built in functions to implement these minimization procedures.

1.4. Outlines of the paper

In this paper, we develop unified simulated methods of inferences for grouped and ungrouped count data using HD distances and it is organized as follows. Asymptotic properties for SMHD methods are developed in Section 2 where consistency and asymptotic normality are shown in section 2.2. Based on asymptotic properties, consistency of the SMHD estimators hold in general but high efficiencies of SMHD estimators can only be guaranteed if the Fisher information matrix of the parametric exists, a situation which is similar to likelihood estimation. One can also viewed the estimators are fully efficient within the class of simulated estimators obtained with the model pmf being replaced by a simulated version. Chi-square goodness of fit test statistics are constructed in Section 2.3. For the ungrouped case, it can be seen as having grouped data but the number of intervals with unit length and the number of intervals is infinite, it is given in section 3 where the ungrouped SMHD estimators are shown to have good efficiencies. The breakdown point for the SMHD estimators remains

at least just as for the deterministic version. A limited simulation study is

included in section 4. First, we consider the Neymann type A distribution and compare the efficiencies of the SMHD estimators versus moment (MM) estimators, simulations results appear to confirm the theoretical results showing that the SMHD estimators are more efficient than the MM estimators based on matching the first two empirical moments with their model counterparts for a selected range of parameters. The Poisson distribution is considered next and the study shows that despite being less efficient than the ML estimator, the efficiency of the SMHD estimators remain high and the estimators are far more robust than the ML estimator in the presence of outliers just as in the deterministic case as shown by Simpson [14] (p805). More works are needed in this direction in general and for assessing the performance SMHD estimators and comparisons with the performances of other traditional estimators in various parametric models in finite samples.

2. SMHD Methods for Grouped data

2.1. Introduction

Pakes and Pollard [16] have developed a very elegant and general theory for establishing consistency and asymptotic normality of estimators obtained by minimizing the length of a random function taking values in an Euclidean space, i.e., by minimizing

(5)

or

(6)

where is a vector of random functions with values in a Euclidean space and is the Euclidean norm and if is a matrix of finite dimension then

. Their theory is summarized by their Theorem 3.1 and

Theorem 3.3 given in Pakes and Pollard [16] (p1038-1043). It is very general and it is clearly applicable for both versions D and S for Hellinger distance with grouped data. Let

(7)

and for HD distance, version D, let

, (8)

and for version S, let

(9)

which can be reexpressed as

. (10)

In general, the intervals’s form a partition of the nonnegative real line

with. Only in section (2.3) where we want to test goodness of fit

for continuous distribution with support of the entire real line used in financial

study, we might let, is the real line.

Let, the vector

of the true parameters is denoted by, the parameter space is assumed to be compact. Clearly, we have point wise convergence in probability with for each for both versions, is nonrandom. Clearly the set up fits into the scopes of their Theorem 3.1 and 3.3 which we shall rearrange the results of these two theorems before applying to version D and version S of Hellinger distance inferences and verify that we can satisfy the regularity conditions of these two Theorems.

2.2. Asymptotic properties

2.2.1. Consistency

We define MHD estimators as given by the vector for version D and for version S but emphasize version S as version D has been studied by Simpson [14] . Both versions can be treated in a unified way using the following Theorem 1 for consistency which is essentially Theorem 3.1 of Pakes and Pollard [16] (p1038) and the proof has been given by the authors.

Theorem 1 (Consistency)

Under the following conditions converges in probability to:

a), the parameter space Ω is compact

b),

c) for each.

Theorem 3.1 states condition b) as but in the proof the authors just use so we state condition b) as as it is easier to use this condition when there is a need to extend to the infinite dimensional case with the space.

An expression is if it converges to 0 in probability and if it is bounded in probability. In version D and version S for Hellinger distance we have occurs at the values of the vector values of the HD estimators, so the conditions a) and b) are satisfied for both versions and compactness of the parameter space Ω is assumed. Also, for both versions only at and otherwise, this implies that there exist real numbers u and v with such that

Therefore, for both versions of whether deterministic or simulated, the minimum Hellinger distance estimators (MHD) are consistent. Theorem 3.1 of Pakes and Pollard [16] is an elegant theorem, its proof is also concise using the norm concept of functional analysis and it allows many results to be unified. Essentially, the same theorem remains valid with the use of the Hilbert space and its norm instead of the Euclidean space and the Euclidean norm. By using and its norm the consistency for the ungrouped SMHD estimators can also be established but further asymptotic results for the ungrouped SMHD estimators will be postponed and given in Section 3.

Asymptotic normality is more complicated in general. For the grouped case, Theorem 3.3 given by Pakes and Pollard [16] (p1040) can be used to establish asymptotic normality for both versions of Hellinger distance estimators. We shall rearrange results of Theorem 3.3 under Theorem 2 and Corollary 1 given in the next section to make it easier to apply for HD estimation using both versions.

Since the proofs have been given by the authors, we only discuss here the ideas of their proofs to make it easier to follow the results of Theorem 2 and Corollary 1 in Section (2.2.2).

For both versions, but is

not differentiable for version S, the traditional Taylor expansion argument cannot be used to establish asymptotic normality of estimators obtained by minimizing. If we assume is differentiable with derivative matrix, then we can define the random function to approximate with

. (11)

is based on expression (8) for version D and it is based on expressions (9-10) for version S. Note that is differentiable for both versions.

Let and be the vectors which minimize and respectively. If the approximation is of the right order then and are asymptotically equivalent. This set up will allow a unified approach for establishing asymptotic for MHD estimation for both versions. For version D, it suffices to let and for version S, let.

Under these circumstances, it suffices to work with and for asymptotic properties of and. A regularity condition for the approximation is of the right order which implies the condition (iii) given by their Theorem 3.3, which is the most difficult to check is given as

. (12)

This condition is used to formulate Theorem 2 below and is slightly more stringent than the condition iii) of their Theorem 3.3 but it is less technical and sufifcient for SMHD estimation. Clearly, for SMHD estimation is as given by expression (9) or expression (10). For simulated unweighted simulated minimum chi-square estimation for this condition to hold, independent samples for each cannot be used, see Pakes and Pollard [16] (p1048). Otherwise, only consistency can be guaranteed for estimators using version S. For version S, the simulated samples are assumed to have size and the same seed is used across different values of to draw samples of size U. We implicitly make these assumptions for SMHD methods. These two assumption are standard for simulated methods of inferences, see section 9.6 for method of simulated moments(MSM) given by Davidson and McKinnon [19] (p383-394). For numerical optimization to find the minimum of the objective function, we rely on direct search simplex methods which are derivative free and the R package already has prewritten functions to implement direct search methods.

2.2.2. Asymptotic normality

In this section, we shall state a Theorem namely Theorem 2 which is essentially Theorem 3.3 by Pakes and Pollard [16] (p1040-1043) with the condition (4) of Theorem 2 given by expression (9) replacing their condition (iii) in their Theorem 3.3, the condition (4) implies the condition (iii) by being more stringent. We also comment on the conditions needed to verify asymptotic normality for the HD estimators based on Theorem 2.

Theorem 2

Let be a vector of consistent estimators for, the unique vector which satisfies.

Under the following conditions:

1) The parameter space Ω is compact, is an interior point of Ω.

2).

3) is differentiable at with a derivative matrix of full rank.

4) for every sequence of positive numbers which converge to zero.

5).

6) is an interior point of the parameter space Ω.

Then, we have the following representation which will give the asymptotic distribution of in Corollary 1, i.e.,

, (13)

or equivalently, using equality in distribution,

. (14)

The proofs of these results follow from the results used to prove Theorem 3.3 given by Pakes and Pollard [16] (p1040-1043). For expression (13) or expression (14) to hold, in general only condition 5) of Theorem 2 is needed and there is no need to assume that has an asymptotic distribution. From the results of Theorem 2, it is easy to see that we can obtain the main result of the following Corollary 1 which gives the asymptotic covariance matrix for the HD estimators for both versions.

Corollary 1.

Let, if then with

,

The matrices and depend on we also adopt the notations,.

We observe that condition 4) of Theorem 2 when applies to Hellinger distance or in general involve technicalities. The condition 4) holds for version D, we only need to verify for version S. Note that to verify the condition 4, it is equivalent to verify

and for version S of Hellinger distance estimation, let

and for the grouped case, it is given by

. (15)

We need to verify that we have the sequence of functions converge uniformly to 0 in probability as and or equivalently, as and.

Note that

We shall outline the approach by first defining the notion of continuity in probability and let which is a compact set. The compactness of this set simplifies proofs and does not appear to be used in previous approaches in the literature. Observe that, it is easy to see that

as. Subsequently we establish being continuous in probability for and using the property that is continuous in probability is attained at a point which belongs to the compact set in probability. This is similar to the property of nonrandom continuous function in real analysis.

Now as which implies and by continuity in probability. Therefore, which means that converges uniformly in probability as. The technical

details of these arguments are given in technical appendices TA1.1 and TA1.2 at the end of the paper, in the section of Appendices.

The notion of continuity in probability has been used in a similar context in the literature of stochastic processes, see Gusalk et al. [25] and will be introduced in the next paragraph and we also make a few assumptions which are summarized by Assumption 1 and Assumption 2 given below along with the notion of continuity in probability. A related continuity notion namely the notion of continuity with probability one has been mentioned by Newey and McFadden [18] in their Theorem 2.6 as mentioned earlier. They also commented that this notion can be used for establishing asymptotic properties of simulated estimators introduced by Pakes [26] . Pakes [26] also has used pseudo random numbers to estimate probability frequencies for some models. For SMHD estimation, we extend a standard result of analysis which states that a continuous function attains its supremum on a compact set to a version which holds in probability. This approach seems to be new and simpler than the use of the more general stochastic equicontinuity condition given by section 2.2 in Newey and McFadden [18] (p2136-2138) to establish uniform convergence of a sequence of random functions in probability. Our approach uses the fact that as the set shrinks to, a property which did not seem to have been

used previously by other approaches to establish as

and. Subsequently, we define the notion of continuity in probability which is similar to the one used in stochastic processes, see Gusak et al. [25] (p33) for a related notion of continuity in probability for stochastic processes.

Definition 1 (Continuity in probability)

A sequence of random functions is continuous in probability at if whenever. Equivalently, for any, there exists a and such that for, whenever. This can be viewed as an extension of the classical

result of continuity in real analysis. It is also well known that the supremum of a continuous function on a compact domain is attained at a point of the compact domain, see Davidson and Donsig [27] (p81) or Rudin [28] (p89) for this classical result. The equivalent property for a random function which is only continuous in probability is the supremum of the random function is attained at a point of the compact domain in probability. The compact domain we study here

is given by and as,. It

might be more precise to use the term sequence of random functions rather than just random function here for the notion of continuity in probability as the random function will depend on n.

Below are the assumptions we need to make to establish asymptotic normality for SMHD estimators and they appear to be reasonable.

Assumption 1

1) The pmf of the parametric model has the continuity property with whenever.

2) The simulated counterpart has the continuity in probability property with whenever. Convergence in probability is denote by.

3) is differentiable with respect to.

In general, the condition 2) will be satisfied if the condition 1) holds and implicitly we assume the same seed is used for obtaining the simulated samples across different values of. For ungrouped data, we also need the notion of differentiability in probability to facilitate the application of Theorem 7.1 given by Newey and McFadden (1994, p2185-2186). Before stating their Theorem 7.1, Newey and McFadden has mentioned the notion of approximate derivative for the use of their Theorem, the definition given below will make it clearer.

Definition 2 (Differentiability in probability)

The sequence of random functions is differentiable with respect to at in probability if, exists and with 1 occurring at the ith entry. Furthermore, the vector is continuous and bounded in probability for all for some. This concept is similar to the notion of

differentiability in real analysis for nonrandom function.

A similar notion of differentiability in probability has been used in stochastic processes literature, see Gusak et al. [25] (p33-34), a more stringent differentiability notion namely differentiability in quadratic mean has also been used to study local asymptotic normality (LAN) property for a parametric family, see Keener [29] (p326). The notion of differentiability in probability will be used in section 3 with Theorem 7.1 of Newey and McFadden [17] to establish asymptotic normality for the SMHD estimators for the ungrouped case. We make the

following assumption for where can be viewed as a proxy model for,

Assumption 2

with the same seed being used across different values of is differentiable in probability with the same derivative vector as where the derivative vector for is

.

This assumption appears to be reasonable, this can be checked by using limit operations as in real analysis with and is continuous in probability.

Since regularity conditions for Theorem 2 and its corollary can be met and they are justified in TA1.1 and TA1.2 in the Appendices, we proceed here to find the asymptotic covariance matrix.

Since for version D is based on expression (8) and for version S is based on expressions (9-10), the asymptotic covariance matrix of version S is just the asymptotic covariance matrix of of version D multiplied by as the simulated sample from is independent

from the sample given by the data, so we can focus on version D and make the adjustment for version S. We need the asymptotic covariance matrix of the

vector first then we can find the matrix and we let for version D and for version S, we shall let.

Recall that form properties of the multinomial distribution, the covariances of and are

and

The covariance matrix of using matrix notations can be expressed as

, (16)

is a diagonal matrix with diagonal elements and the vector is the transpose of and is the identity matrix of dimension with. Using the delta method the asymptotic covariance matrix of of version D is simply the asymptotic covariance matrix of which is given by

, (17)

and the asymptotic covariance matrix of, version S is

. (18)

We then have the vector of HD estimators version D and S given respectively by and with asymptotic distributions given by

(19)

,

is the model Fisher information matrix using grouped data as due to using. Let,

,

so

with

.

Therefore for version S,

(20)

the simulated sample size is.

Note that for version D, the HD estimators are as efficient as the minimum chi-square estimators or ML estimators based on grouped data. The overall asymptotic relative efficiency (ARE) between version D and S for HD estimation is

simply ARE = and we recommend to set to minimize the loss of efficiency due to simulations.

An estimate for the covariance matrix

The asymptotic covariance matrix of can be estimated if we can estimate. Using a result given by Pakes and Pollard (1989, p1043), an estimate for is the matrix

, (21)

with 1 occurring at the ith entry of the vector and, and in general we can let. Note that the columns of estimate the corresponding partial derivatives given by the columns of .

For ungrouped data and for version D, it is equivalent to choose with unit length and let. If we choose and let and note that and the is Fisher information matrix for ungrouped data with elements given by

(22)

and. We can foresee that the HD estimators are as efficient as ML estimators for version D, a result which is already obtained by Simpson [14] . We postpone till section (3) for a more rigorous approach to justify the related result for version S using Theorem 7.1 given by Newey and McFadden [17] . The SMHD estimators given by for ungrouped data will be shown to have the property

.

Section 3 may be skipped for practitioners if their main interests are only on applications of the results.

2.3. Chi-square Goodness of Fit test Statistics

2.3.1. Simple Hypothesis

In this section, the Hellinger distance is used to construct goodness of fit test statistics for the simple hypothesis

H₀: data comes from a specified distribution with distribution, can be the distribution of a discrete or continuous distribution. The chi-square test statistics and their asymptotic distributions are given below with

(23)

(24)

The version S is of interest since it allows testing goodness of fit for discrete or continuous distribution without closed form pmfs or density functions, all we need is to be able to simulate from the specified distribution. We shall justify the asymptotic chi-square distributions given by expression (23) and expression (24) below.

Note that

and

for version D. For version S,

.

Using standard results for distribution of quadratic forms and the property of the operator trace of a matrix with , see Luong and Thompson [30] (p247); we have the asymptotic chi-square distributions as given by expression (23) and expression (24). On how to choose the intervals, the problem is rather complex as it depends on the type of alternatives we would like to detect. We can also follow the recommendations of the Pearson’s statistics, see Greenwood and Nikulin [31] ; also see Lehmann [32] (p341) for more discussions and references on this issue.

2.3.2. Composite hypothesis

Just as the chi-square distance, the Hellinger distance can also be used for construction of the test statistics for the composite hypothesis,

H₀: data comes from a parametric model, can be a discrete or continuous parametric model. The chi-square test statistics are given by

, (25)

for version D and for version S,

(26)

where and are the vector of HD estimators which minimize version D and version S respectively and assuming. To justify these asymptotic chi-square distributions, note that we have for version D,

. It suffices to consider the asymptotic distribution of as we have the following equalities in distribution,

, as given by expression (11). Also, using expression (11) and expression (13),

which can be reexpressed as

or

With

,

is based on expression (8) for version D. Consequently,

by noting

,

using and the matrix is of rank with the rank of the matrix is also equal to its trace. The argument used is very similar to the one used for the Pearson’s statistics, see Luong and Thompson [30] (p249).

For version S,

and

with

,

is based on expressions (9-10) for version S. This justifies the asymptotic chi-square distribution for version S as given by expression (25) and expression (26). This version is useful for model testing for nonnegative continuous models without closed form expression densities, see Luong [33] for some positive infinitely divisible distributions without closed form densities used in actuarial sciences. It is also suitable for testing models with support on the real line used in finance such as the jump diffusion model as given by Tsay [34] (p311-319), for example. All we need is to be able to simulate from the model.

3. SMHD Methods for Ungrouped Data

For the classical version D with ungrouped data, Simpson [14] (p806) in the proof of his Theorem 2 has shown that we have equality in probability of the following expression by letting

be the vector of partial derivatives with respect to of and we have

(27)

with and is the vector of the

score functions with covariance matrix which is the Fisher information matrix.

For version D, we then have

or equivalently

.

Therefore, we can conclude that which is

the result of Theorem 2 given by Simpson [14] (p804) which shows that the MHDE estimators are as effcient as the maximum likelihood (ML) estimators.

For version S with ungrouped data, it is more natural to use Theorem 7.1 of Newey and McFadden [17] (p2185-2186) to establish asymptotic normality for SMHD estimators. The ideas behind Theorem 7.1 can be summarized as follows. In case of the objective function is non smooth and the estimators is the vector which is obtained by minimizing, we can consider the vector which is obtained by minimizing a smooth function which approximates if is differentiable in probability at with the derivative vector given by. For SMHD estimation,

(28)

with its equivalent expression given by expression (3).

Also, if and assume that is non random and twice differentiable with second derivative matrix with, attains its minimum at then we can define

.

The vector which minimizes can be obtained explicitly as is a quadratic function of, it is given by and using equality in distribution

.

If the remainder of the approximation is small, we also have

.

Before defining the remainder term, note that the following approximation can be viewed as equivalent with

as using, is minimized at.

For the approximation to be valid, we define

and requires as as indicated by the

proofs of Theorem 7.1 given by Newey and McFadden. The following Theorem 3 is essentially Theorem 7.1 given by Newey and McFadden but restated with estimators obtained by minimizing an objective function instead of maximizing an

objective function and requires which is slightly

more stringent than the original condition v) of their Theorem 7.1. We also require compactness of the parameter space. Newey and McFadden do not use this assumption but with this assumption, the proofs are less technical and simplified. It is also likely to be met in practice.

Theorem 3

Suppose that, and

1) is minimized at;

2) is an interior point of the parameter space;

3) is twice differentiable at with nonsingular matrix;

4);

5) as. Then

The regularity conditions (1-3) of Theorem 3 can easily be checked. The condition 4 follows from expression (27) established by Simpson [14] . The condition 5 might be the most difficult to check as it involve technicalities and it is verified in TA2 of the Appendices. By assuming all can be verified, we apply Theorem 3 for SMHD estimation with.

The objective function is as defined by expression (3),

the matrix of second derivative of is

and it can be seen that

,

by performing limit operations to find derivates as in real analysis and using Assumption 1 and Assumption 2. Therefore, we have the following equality in distribution using the condition 4) of Theorem 3 and expression (27)

(29)

which is similar to the grouped case.

Now with with the size of the simulated sample is and the simulated sample is independent of the sample given by data, we can argue as for the grouped case to conclude

. (30)

One might want to define the extended Cramér-Rao lower bound for simulated method estimators to be; with this definition, the asymptotic covariance matrix of SMHD estimators attains this bound just as the asymptotic covariance matrix of ML estimators attain the classical Cramér-Rao lower bound. The factor is a common factor which also appears in

other simulated methods, it can be interpreted as the adjustment factor when estimators are obtained via minimizing a simulated version of the objective function instead of the original objective function with the model distribution being replaced by a sample distribution using a simulated sample, see Pakes and Pollard [16] (p1048) for the simulated minimum chi-square estimators, for example. Clearly, can also be estimated numerically as in the grouped case which is given in section (2). Results of Theorem 2 and Corollary 1 allow us to establish asymptotic normality of the MHD estimators for both versions in a unified way.

We close this section by showing the asymptotic breakdown point of SHMD estimators is the same as HMD estimators under the true model with

by using the argument used by Simpson for the version D of HD estimators,

see Simpson [14] (p805-806) and assuming only the original data set might be contaminated, there is no contamination coming from simulated samples. This assumption appears to be reasonable as we can control the simulation procedures. We focus only on the strict parametric model and the set up is less general than the one considered by Theorem 3 of Simpson [13] (p805) which also includes distributions near the parametric model.

Let be the contaminated distribution function defined as

, where is the true distribution function and the distribution is introduced to contaminate the model. The pmfs of and are given respectively by and. The asymptotic breakdown point is the smallest value which makes. The vector minimizes with respect to the objective function

.

Now with the same seed used across, can be viewed as a proxy pmf for the true parametric model. We let and show that this will imply in probability. As is the vector which minimizes SHD or maximizes clearly. Now observe that

but

as which implies. So, in probability, we have the lower bound

.

With,

using the inequality with, we have the upper bound inequality

The last inequality follows from the assumption that since which implies the two pmfs and are not close according to the discrepancy measure using SHD as, an argument also used by Simpson [14] to justify his expression, see Simpson [14] (p805-806).

Using, we might conclude in probability we have the inequalities which implies in

probability under the true model which is similar to version D. The only difference is here we have an inequality in probability. From this result, we might conclude that the SMHD estimators preserve the robustness properties of version D and the loss of asymptotic efficiency comparing to version D can be minimized if.

4. Numerical Issues

4.1. Methods to Approximate Probabilities

Once the parameters are estimated, probabilities can be estimated. For situations where recursive formulas exist then Panjer’s method can be used, see Chapter 9 of the book by Klugman et al. [4] . Otherwise, we might need to approximate probabilities by simulations or by analytic methods.

In this section, we discuss some methods for approximating probabilities for a discrete nonnegative random variable X with pgf which can be used if a recursion formula for is not available. The saddlepoint method and the method based on inverting the characteristic function can be used.

See Butler [35] (p8-9) for details of the saddlepoint approximation. It can be described as using to approximate, with

.

The saddlepoint is defined implicitly, using the pgf, as the solution of, and with and . The function is the cumulant function.

If the cumulant function does not exist, an alternative method which is based on the characteristic function, as described by Abate and Whitt [36] (p32), can be used.

4.2. A Limited Simulation study

4.2.1. Neymann Type A distribution

As an example for illustration we choose the Neymann Type A distribution with the method of moments (MM) estimators for and which have been given

by Johnson et al. [8] . The MM estimators are given by and

with the sample mean and variance given respectively by and. The MM estimators are classical moment estimators. We perform a limited simulation study to compare the performance of the SMHD estimator which is given by

vs the MM estimators given by.

For the range of parameter values, we let,

are used in the study. For applications often the parameter for the mixing distribution much smaller than the parameter. The SMHD estimators seem to perform much better than the MM estimators, in general. The results are displayed in Table A. The criterion for overall relative

efficiency used is the ratio with denotes

the mean square error of the estimator inside the parenthesis. The mean square error of an estimator for is defined as

.

The ratio ARE can be estimated using simulated data and they are displayed in Table A. Due to limited computing facilities, we only draw samples of size and the simulated sample is fixed at, and the results are summarized using Table A. It takes around one minute using a laptop computer for obtaining the SMHD estimators for one simulated sample. The MM estimators appear to perform reasonably well for some samples but display erratic results for some other samples which account for the loss of efficiency of the MM estimators. Also, the parameter is not well estimated by the moment method but it gives reasonably good estimates for the parameter in general. The MM estimators are based on the sample mean and variance and these statistics are known to be nonrobust. If outliers are present, the MM estimators again might become erratic. The mean square errors (MSE) for estimating the parameters and the corresponding ratios ARE are estimated using the simulated samples and the AREs are displayed in Table A.

4.2.2. Poisson distribution

For the Poisson model with parameter we compare the performance of the MLE for which is the sample mean vs the SMHD estimator

using the ratio for. For the Poisson

model, the information matrix exists and we can check the efficiency and robustness of the SHD estimator and compare it with the ML estimator which is the sample mean. Since there is only on parameter estimate we are able to fix

Asymptotic relative efficiency between MLE and SHD, for the Poisson model with parameter.

Asymptotic relative efficiency between MLE and SHD for the Poisson model when 10% of data coming from the discrete positive distribution with parameter and, i.e.,.

U = 10000 for the simulated sample size from the Poisson model without slowing down the computations. It appears overall the SHD estimators performs very well for the range of parameters often encountered in actuarial studies, here we observe that the asymptotic efficiencies range from 0.7 to 1.1. We also study a contaminated Poisson model () with observations coming from the Poisson model () and of observations coming from a discrete positive stable (DPS) distribution with the parameter for and has the same value of the Poisson model. We compare the performance of the sample mean for which is the ML estimator vs the SMHD estimator using the contaminated model Poisson model as described and estimate the

for to compare the robustness of

the SMHD estimator vs ML estimator in presence of contamination. The sample mean looses its efficiency and becomes very biased. The results are given at the bottom of Table A which shows that the performs much better than the sample mean which is the ML estimator. For drawing simulated samples from the DPS distribution, the algorithm given by Devroye [37] is used.

5. Conclusion

More simulation experiments to further study the performance of the SMHD estimators vs commonly used estimators across various parametric models are needed and we do not have the computing facilities to carry out such large scale studies. Most of the computing works were carried out using only a laptop computer. So far, the simulation results confirm the theoretical asymptotic results which show that SMHD estimators have the potential of having high efficiencies for parametric models with finite Fisher information matrices and they are robust if data is contaminated; the last feature might not be shared by ML estimators.

Acknowledgements

The helps received from the Editorial staffs of OJS which lead to an improvement of the presentation of the paper are gratefully acknowledged.

Cite this paper

Luong, A., Bilodeau, C. and Blier-Wong, C. (2018) Simulated Minimum Hellinger Distance Inference Methods for Count Data. Open Journal of Statistics, 8, 187-219. https://doi.org/10.4236/ojs.2018.81012

References

Appendices

Technical Appendix 1 (TA1)

TA 1.1

In this technical appendix, we shall show that a sequence of random functions which is continuous in probability and bounded in probability on a compact set will attain its supremum on a point of in probability. Pick a sequence in with the property. Since is compact we can extract a subsequence from with the property which belongs to. This property in real analysis is also known under the name Bolzano-Weirstrass theorem. We then have and.

TA 1.2

In this technical appendix, we shall show that the sequence of function is continuous in probability and for the grouped case of Section (2.2.2), for the grouped data case can also be expressed as

The first two terms of the RHS of the above equation are bounded in probability as they have a limiting distributions and this implies the third term is also bounded in probability by using Cauchy-Schwartz inequality. Now using the conditions of Assumption 1 of Section (2.2.2) and implicitly the assumption of the same seed is used across different values of, we then have as,

and

From the above property, it is clear that, is continuous in probability, and using TA1.1 we conclude that there exists which

belongs to and but as,. Therefore, , as.

The justifications for the ungrouped case are similar using the same type of arguments but with the use of Theorem 7.1 given by Newey and McFadden [17] and will be given in TA2.

Technical Appendix 2 (TA2)

In this technical appendix we shall verify the condition

as for SMHD estimation using ungrouped data. Despite, we will keep and define the sequence of functions then it will allow us to express. Now with, is differentiable in probability at. The derivative vector for at is simply as it can be seen by performing limit operations as in real analysis and using Assumption 1 and Assumption 2 in Section 3. Therefore, we have as by using definition of the derivative. Since is approximable by which is bounded in probability in a neighborhood including, using expression (27), we might assume is bounded in probability for. We might also assume that as, using Dominated Convergence Theorem (DCT) with when, as defined by expression (28) of Section 3, the summand of satisfies the following inequalities

,

hence the use of DCT is justified. Therefore, is continuous in probability for all.

Now if we define, is continuous in probability for all which belongs to. Consequently, with as the set is compact. As, , , , this establishes the result and the argument used is similar to the one used in TA1.2 for the grouped data case.