ABSTRACT

The prevalence of a disease in a population is defined as the proportion of people who are infected. Selection bias in disease prevalence estimates occurs if non-partici- pation in testing is correlated with disease status. Missing data are commonly encountered in most medical research. Unfortunately, they are often neglected or not properly handled during analytic procedures, and this may substantially bias the results of the study, reduce the study power, and lead to invalid conclusions. The goal of this study is to illustrate how to estimate prevalence in the presence of missing data. We consider a case where the variable of interest (response variable) is binary and some of the observations are missing and assume that all the covariates are fully observed. In most cases, the statistic of interest, when faced with binary data is the prevalence. We develop a two stage approach to improve the prevalence estimates; in the first stage, we use the logistic regression model to predict the missing binary observations and then in the second stage we recalculate the prevalence using the observed data and the imputed missing data. Such a model would be of great interest in research studies involving HIV/AIDS in which people usually refuse to donate blood for testing yet they are willing to provide other covariates. The prevalence estimation method is illustrated using simulated data and applied to HIV/AIDS data from the Kenya AIDS Indicator Survey, 2007.

Keywords:

Disease Prevalence, Missing Data, Non-Participant, Logistic Regression Model, Prevalence Estimates, HIV/AIDS

1. Introduction

Prevalence in epidemiology is the proportion of a population found to have a condition. It is difficult to over-emphasize the importance of obtaining accurate information on the prevalence. Accurate estimates of disease prevalence are critical for tracking the epidemic, designing and evaluating prevention and treatment programs, and estimating resource needs. A potential threat to the validity of survey-based prevalence estimates is that not all individuals eligible to participate in a survey can be contacted, and some who are contacted do not consent to be tested [1] .

If any data on any variable from any participant are not present, then the researcher is dealing with missing or incomplete data. The problem of missing data is a common occurrence in most medical research [2] . In clinical trials and observational studies, complete data are often not available for every subject. Missing data may arise because of many circumstances: the unavailability of converting measurements, survey nonresponse, study subjects failing to report to a clinic for monthly evaluations, respondents refusing to answer certain items on a questionnaire [3] . Respondents may refuse to answer a question because of privacy issues or the person taking the survey does not understand the question. Perhaps, the respondent would have answered, but the answer, he or she might have given was not one of the options presented. Perhaps there wasn’t enough time to complete the questionnaire or the respondent just lost interest.

It is rare, even under the strictest protocols, to complete a biological or medical study with absolutely no missing values. While many investigators consider missing data a minor nuisance, ignoring them is potentially very problematic [4] . In fact, investigators should attempt to use all available data to perform the most efficient study possible, to reduce bias, and to provide the most valid estimates of risk and benefit. A bias which is known as systematic error, may result directly from the inappropriate handling of missing values. A primary goal of the analysis of a medical study is to minimize bias so that valid results are presented and appropriate conclusions are drawn. While bias may be introduced into research through several other mechanisms (e.g., study design, patient sampling, data collection, and or other aspects of data analyses), naive methods of handling missing data may substantially bias estimates while reducing their precision and overall study power, any of which may lead to invalid study conclusions. When a large proportion of missing data exist or when there are missing data for multiple variables, these effects may be dramatic. Despite these concerns and the development of sophisticated methods for handling missing data that allow for valid estimates for preservation of study power, many studies continue to ignore the potential influence of missing data, even in the setting of clinical trials [4] .

Previous authors have suggested that non-participation may lead to bias in human immunodeficiency virus (HIV) prevalence estimates, but official estimates of HIV prevalence in sub-Saharan Africa relies heavily on population-based surveys, which often have low participation rates [1] . An analysis of the Demographic and Health Surveys (DHS), which are the most common nationally representative surveys for HIV prevalence in sub-Saharan Africa, reveals average rates of non-participation in HIV testing of 23% for adult men and 16% for adult women in the region, with a high of 37% for men in Zimbabwe 2005-2006 and a low of 3% for women in Rwanda 2005 [5] , and the most recent national population-based survey in South Africa reported an overall non-par- ticipation rate of 32% for HIV testing among adults [1] . Analyses of the DHS have adjusted HIV prevalence estimates for testing non-participation by imputing missing HIV test results with probit regressions, controlling for differences in observed characteristics between testing participants and non-participants, such as gender, urban residence, wealth and indicators of sexual behavior [1] [5] . Based on this conventional imputation approach, non-participants were estimated to have higher HIV prevalence than participants in about half of the DHS examined, but this did not result in substantially different estimates of overall HIV prevalence when compared with the complete-case estimates that ignored missing observations [5] . These results have been interpreted to mean that non-participation in HIV testing surveys is likely to have minimal impact on prevalence estimates [1] [5] . However, the conventional imputation approach has two important limitations. First, it assumes that no unobserved variables associated with HIV status influence participation in HIV testing. Second, it ignores regression parameter uncertainty in the imputation model, resulting in confidence intervals (CI) that are too small.

2. Method

To predict the values for the missing data and to identify the underlying determinants which have significant effect on the prevalence, a statistical model will be employed. Therefore, due to the binary nature of the outcome variable in this study, being positive or negative, a binary logistic regression model will be employed for the given data. One of the main applications of logistic regression is to determine or forecast the chance of the occurrence of a particular outcome of the response variable on the basis of independent or explanatory variables by fitting a given data to logit function. Logistic regression has been used in epidemiological research, where often the outcome variable is presence or absence of some disease. In this study, we restrict the models to a case where the response variable is binary and make an assumption that all the covariates are available. We will demonstrate how the prevalence estimated can be improved by using the predicted missing values. We develop a two stage approach to improve the prevalence estimates; in the first stage, we use the logistic regression model to predict the missing binary observations and then in the second stage we recalculate the prevalence using the observed binary data and the imputed binary data. The prevalence estimation method is illustrated using simulated data and applied to HIV/AIDS data from the Kenya AIDS Indicator Survey 2007.

Prevalence Estimation

Consider a population that, consists of n living individuals who can be infected or not by a disease. The disease status of individual i is represented by the binary indicator y_i, which is equal to 1 if individual i is positive and is equal to 0 otherwise.

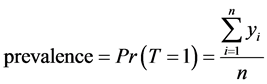(1)

where T is a random variable that represents the variability of the indicator of a disease status in the population.

Thus, disease prevalence is just the proportion of infected people. Our aim is to estimate from sample surveys when the disease status may be missing for some cases.

By the law of total probability, we can write disease prevalence as:

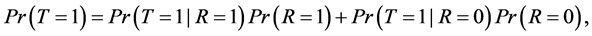(2)

where R is a binary indicator equal to 1 if disease status is known and to 0 otherwise.

The missing data problem arises because the data tell us nothing about

.

Let I be the set of indices for the observed values and J be set of indices for the missing values.

From Equation (2) and the fact that, we have:

Since

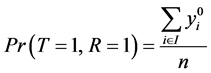
And

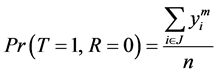
(3)

From Equation (6), to estimate the prevalence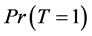, we will find the estimated missing values.

Let’s consider:

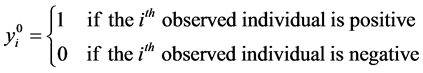
Note that

where is the random variable associated to the observed values.

By making an assumption that all the covariates are fully observed, we can fit a logistic regression model by considering only the observed data and the corresponding variables.

(4)

where 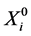is the vector of the explanatory variables such that R = 1 and is the vector of parameters in the model.

From model (4), we can now estimate the parameters.

After having estimated the coefficients in this regression, it is standard practice to assess the significance of the variables in the model. This usually involves testing a statistical hypothesis in order to determine whether the independent variables in the model are “significantly” related to the outcome variable. One approach to testing for the significance of the coefficient of a variable in any model is to see whether the model that includes the variable in question tells us more about the outcome (or response) variable than a model that does not include that variable.

This can be done by doing a comparison between the observed values of the response variable with those predicted by each of the two models; the first with and the second without the variable in question. The mathematical function used in comparing the observed and predicted values depends on the particular problem. If the predicted values with the variable in the model are better, or more accurate in some sense, than when the variable is not in the model, then we can say that the variable in question is significant.

For the purposes of assessing the significance of an independent variable we compute the value of the following statistic:

(5)

The first step in this process is usually to assess the significance of the variables in the model. The likelihood ratio test for overall significance of the k coefficients for the independent variables in the model is performed based on the statistic G given in (4). Under the null hypothesis that the k “slope” coefficients for the covariates in the model are equal to zero, the distribution of G is chi-square with k degrees of freedom.

Rejection of the null hypothesis (that all of the coefficients are simultaneously equal to zero) has an interpretation analogous to that in multiple linear regression; we may conclude that at least one, and perhaps all k coefficients are different from zero.

Before concluding that any or all of the coefficients are nonzero, we may wish to look at the univariate Wald test statistics which is obtained by comparing the maximum likelihood estimate of the slope parameter, , with an estimate of its standard error,

(6)

Under the hypothesis that an individual coefficient is zero, these statistics will follow the standard normal distribution. Thus, the value of these statistics may give us an indication of which of the variables in the model may or may not be significant.

Considering that the overall goal is to obtain the best fitting model while minimizing the number of parameters, the next logical step is to fit a reduced model, containing only those variables thought to be significant, and compare it with the full model containing all the variables. The likelihood ratio test comparing these two models is obtained using the definition of G given in (4).

It has a distribution that is chi-square with k degrees of freedom under the hypothesis that the coefficients for the variables excluded are equal to zero and has a P value of P. If the P value is large, we conclude that the reduced model is as good as the full model.

Now from that model, we estimate the probabilities, i.e. the probabilities of success for each missing outcome as follows:

(7)

where are the values of the coefficients estimated from model (4) and is the vector of the explanatory variables such that R is equal to 0.

is called the maximum likelihood estimate of. This quantity provides an estimate of the conditional probability that is equal to 1, given that x is equal to. As such, it represents the fitted or predicted value for the logistic regression model.

Once we have the estimated probabilities, let us consider the values of denoted by

(8)

where α is based on the accuracy and the ability of prediction of the model fitted in a given data. Most of the time α = 0.5.

This means that from those who were missing, if the predicted probability is greater than or equal to α, then one can conclude that the individual i is positive and if is strictly less than α, then that individual i is negative. Once we have the which is the dataset containing the imputed missing values, then we can now calculate the estimated prevalence denoted by {Prevalence}_est using the full data set containing

3. Simulated Data

We simulate 3000 binary observations from a logistic regression model where the outcome variable is called Disease and seven covariates such that Age, Sex, Ever married, Urban, Educational level, Condom use and other In the first time, we assume that both the outcome variable and the covariates are fully observed, then we compute the true prevalence. After that, we consider a case where the variable of interest (response variable or outcome variable) is binary and some of the observations are missing and assume that all the covariates are fully observed. In this simulation study, we consider two steps. Firstly, we create randomly 10%, 20%, 30% and 50% of missing data along the outcome variable over 1000 simulation runs using Monte Carlo simulation. Now after creating these missing values, we use the method discribed above to estimate the prevalence over the 1000 simulation and then take the average estimates of the prevalence for each of these four scenarios. Secondly we only create missing values among those whose disease status is positive to examine the sensitivity to a non random missing data. We also use our method to estimate the prevalence. It is well known that it is possible to estimate the probability of occurrence of disease status from a logistic model. The estimates prevalence without the missing values and the estimates prevalence from our method are further compared with the true prevalence. A Wald test statistic based on the parameter estimate divided by its standard error estimate was used to calculate the proportion of rejections for a Wald test for the null hypothesis that the true parameter is equal to the chosen parameter. When the null hypothesis was that the true parameter value was zero, a likelihood ratio test for the significance of the variable was also computed.

These values of W_j in Equation (5) are given in the fourth column in Table 1. Under the hypothesis that an individual coefficient is zero, these statistic will follow the standard normal distribution. The p-values are given in the fifth column of Table 1.

If we use a level of significance of 0.05, then we can conclude that only the variables condom use, Sex and Age are significant and the others are not significant.

If our goal is to obtain the best fitting model while minimizing the number of parameters, the next logical step is the reduced model containing only those variables thought to be significant, and compare it to the full model containing all the variables. The results of fitting the reduced model are given in Table 2.

The value of the statistic comparing the models in Table 1 and in Table 2 is G = −3.7454 which has a p-value, where k is the number of degrees of freedom in this case. Since the p-value is large, exceeding 0.05, we conclude that the

reduced model is as good as the full model. Thus there is no advantage to include the others variables in the model.

Simulation Results

Table 3 displays the average estimates of the prevalence based on our method, their bias and their 95% confidence intervals and the average estimates of the prevalence without the missing values over 1000 simulation runs using Monte Carlo simulation. These are compared to the true prevalence (0.603) shown in the last line of this table, which use the full dataset before creating the missing values from the disease status. We find that these average estimates of the prevalence based on our method described above are almost identical to those in column 2 which were based only on observations without missing data. Theses averages estimates prevalence correspond are both closed to the true prevalence. We note also that the prevalence obtained by ignoring the missing values and the estimates prevalence obtained from our method are very similar. The estimates prevalence based on our approach presented similar estimates prevalence that are closed to the true prevalence. From these results we can see that if the missing values are created randomly or involves only those who are negative, the prevalence without the missing values is closed to the true prevalence, means that the true prevalence might not be affected. However, our method can still be used to estimate the prevalence for some missing cases as shown in the table. There are two other important features of these results. First, we find that the estimates prevalence based on this approach and the one obtained by ignoring the missing cases are almost identical to the true prevalence. Second, the confidence intervals obtained from our method contains always the true

prevalence. These confidence intervals are not so wide, and they include the true prevalence, indicating that the uncertainty to rule out selection bias is not higher. When the amount of missing observations increased, we realize that our method still continued to produce almost unbiased estimates. However, our approach is easy to implement, it does not require any assumptions about the nature of the missing data, and it allows to obtain reliable intervals from a statistical point of view. Therefore, we conclude that even if the prevalence without the missing data is closed to the true prevalence, our method can still be used to find the estimated prevalence that will be closed to the true prevalence.

Now let us consider the case where we assume that all the missing observations are positives (see Table 4).

Table 5 shows the estimate prevalence when there are only some missing cases among those whose disease status is positive. To examine the sensitivity to a non random missing data, missing values were created among those whose disease status is positive. Even if it is rare, it is possible because individuals might know they are positive because they have been tested before or fear they are positive because of private information on own sexual behavior. Those who refuse to take the test may simply not believe that the results cannot be traced back to the individual, and they may fear for exposure of being found out to be infected with the disease. This fear is likely to be higher among those with high-risk behavior, which in turn is an unobserved determinant of the disease-status. For the first time, we use the full database without any missing values and calculate the true prevalence. For the second time, we create 10%, 20%, 30%,

40% and 50% of missing values, then we compute the prevalence without the missing values for each of these four scenarios. Finally, we use the method described above to estimate the prevalence using both the observed values and the imputed missing values. Using simulated data, we find that when the missing cases are among those whose disease status is positive, the true disease prevalence can be affected by the presence of missing values. Our results show that the estimated prevalence from the method described above is better than the prevalence calculated by ignoring the missing values. As the number of missing values increases as the prevalence without those missing values decreases. According to our results, the prevalence could be much lower, as a larger part of the non respondents could be infected. This can be seen from the table by comparing the prevalence calculated by ignoring the missing values from the true prevalence. If we ignore the missing data and compute directly the prevalence from the observed data we realize that the prevalence can be different from the true prevalence because of the missing data. When the number of missing values is higher, the estimates prevalence from our method are significantly higher than the prevalence without the missing values. As we can see from the table, an important finding is that when the number of missing values is higher, the estimates prevalence without the missing values substantially underestimate the true prevalence. But from the table, when using our method to estimate the prevalence by using the full dataset containing both the observed and the predicted missing values, we obtain a prevalence that is very closed to the true prevalence. We can see also from the table that the true prevalence is always lying inside the confidence interval. Thus method described in this study can still be used to estimate the disease prevalence when there are some missing cases.

4. Data

The 2007 KAIS was conducted among a representative sample of households selected from all eight provinces in the country, covering both rural and urban areas. A household was defined as a person or group of people related or unrelated to each other who live together in the same dwelling unit or compound (a group of dwelling units), share similar cooking arrangements, and identify the same person as the head of household. The household questionnaire was administered to consenting heads of sampled, occupied households. All women and men aged 15 - 64 years in selected households who were either usual residents or visitors present the night before the survey were eligible to participate in the individual interview and blood draw, provided they gave informed consent. For minors aged 15 - 17 years, parental consent and minor assent were both required for participation. Participants could consent to the interview and blood draw or to the interview alone. The inclusion criteria may have captured non-Kenyans living as usual residents or visitors in a sampled household. Military personnel and the institutionalized population (e.g. imprisoned) are typically not captured in similar household-based surveys may have been included in the 2007 KAIS if at home during the survey.

Administratively, Kenya is divided into eight provinces. Each province is divided into districts, each district into divisions, each division into locations, each location into sublocations, and each sub-location into villages. For the 1999 Population and Household Census, the Kenya National Bureau of Statistics (KNBS) delineated sub-locations into small units called Enumeration Areas (EAs) that constituted a village, a part of a village, or a combination of villages. The primary sampling unit for Kenya’s master sampling frame, and for the 2007 KAIS, is a cluster, which is constituted as one or more EAs, with an average of 100 households per cluster.

The master sampling frame for the 2007 KAIS was the National Sample Survey and Evaluation Program IV (NASSEP IV) created and maintained by KNBS. The NASSEP IV frame was developed in 2002 based on the 1999 Census. The frame has 1800 clusters, comprised of 1260 rural and 540 urban clusters. Of these, 294 (23%) rural and 121 (22%) urban clusters were selected for KAIS. The overall design for the 2007 KAIS was a stratified, two-stage cluster sample for comparability to the 2003 KDHS. The first stage involved selecting 415 clusters from NASSEP IV and the second stage involved the selection of households per cluster with equal probability of selection in the rural-urban strata within each district. The target of the 2007 KAIS sample was to obtain approximately 9000 completed household interviews. Based on the level of household non-response reported in the 2003 KDHS (13.2% of selected households), 10,375 households in 415 clusters were selected for potential participation in the 2007 KAIS.

Sample size N = 11338

Summary of the HIV status.

Now we can analyze the fitting and interpret what the model (Table 6) is telling us. As for the statistically significant variables, all the variables have a small p-value suggesting a strong association of these variables with the probability of being positive.

The difference between the null deviance and the residual deviance shows how our model is doing against the null model (a model with only the intercept). The wider this gap, the better. Analyzing the Table 7, we can see the drop in deviance when adding each variable one at a time. A large p-value here indicates that the model without the variable explains more or less the same amount of variation. From the table, we can see that these variables are significant according to their p-value.

Results

This Table 8 shows the HIV estimated prevalence from Kenya when there are some missing cases by using our method described above. Using HIV/AIDS data from the Kenya AIDS Indicator Survey, 2007 HIV where there are some missing cases along the outcome variable, we find that the true HIV prevalence might be affected by the presence of missing as shown in our simulation studies. Our results show that the estimate prevalence from our method is higher than the prevalence calculated by ignoring those missing values. According to the simulation studies, the estimates prevalence from our method are always closed to the true prevalence and the confidence intervals contain

also true prevalence, thus we can conclude that this estimate prevalence (0.095) from our method would be closed the true prevalence which could be contained in the confidence interval (0.090 - 0.101) from the table.

5. Conclusion

Incomplete data are a pervasive problem in medical research, and ignoring them or handling them inappropriately may bias study results, reduce power and efficiency. Appropriate handling of censored values in medical research specially when dealing with prevalence should be a substantial concern of investigators, and planning for the integration of valid incomplete data methods into the analysis is important. This paper confirms that non-participation in disease testing may be an important source of bias in disease prevalence estimates. However, our approach is easy to implement. It does not require many assumptions, and it allows to obtain the estimated prevalence and reliable confidence intervals from a statistical point of view. This method allows to get disease estimated prevalence that can be closed to the true prevalence. Moreover, we stress the fact that it is important to well-design surveys to reduce non response, either unit and item non response. It is also critical to include in the data information, such as interviewer’s characteristics, fieldwork procedures etc, as they can be used as instrumental variables.

Acknowledgements

I would like to thank Dr. Ngesa Owino Oscar and Prof. Abdou Ka Diongue, my supervisors for supporting my work. I would also like to thank Prof. Mwita, my coordinator for his constant encouragement. I would like to thank the administration staff and Prof. Gabriel Mogoma, director PAUISTI, for their sincere and valuable guidance and encouragement extended to us. We are grateful for the support provided by Cheikh Loucoubar, Mareme Diarra and Mamadou Tamsir Diop at Institut Pasteur de Dakar.

Cite this paper

Seck, E.M., Oscar, N.O. and Diongue, A.K. (2016) Improving Disease Prevalence Estimates Using Missing Data Techniques. Open Journal of Sta- tistics, 6, 1110-1122. http://dx.doi.org/10.4236/ojs.2016.66090

References