ABSTRACT

In this paper, an efficient shrinkage estimation procedure for the partially linear varying coefficient model (PLVC) with random effect is considered. By selecting the significant variable and estimating the nonzero coefficient, the model structure specification is accomplished by introducing a novel penalized estimating equation. Under some mild conditions, the asymptotic properties for the proposed model selection and estimation results, such as the sparsity and oracle property, are established. Some numerical simulation studies and a real data analysis are presented to examine the finite sample performance of the procedure.

Keywords:

Partially Linear Varying Coefficient Model, Mixed Effect, Penalized Estimating Equation

1. Introduction

With the effort to reduce the risk of model misspecification, more flexible nonlinear and non/semiparametric models have been proposed for independent and subject- dependent data. See, for example, [1] introduced the varying coefficient model. Reference [2] and [3] studied the partially linear varying coefficient (PLVC) model and single index model, respectively, for longitudinal data. For longitudinal data, see [4] for an intensive review.

As a natural extension of [5] , which used marginal model for longitudinal data analysis, a random effect method is developed when considering within-subject correlation and further shrinkage estimation. In the literatures in longitudinal data study, random effect method has received relatively enough attention. See, for example, [6] - [9] and so on. Some advantages of random effect method were mentioned in [3] including its computation efficiency.

For the special case of PLVC model with random effect, an important problem is to choose the significant covariant variable. Shrinkage estimation based on regularization has attracted lots of interest. See, for example, [10] - [13] . Also, some extensions of the variable selection under the regularization framework to varying coefficient models include, [5] [14] - [16] . In this article, the variable selection problem for PLVC model with random effect is investigated. Because of the obvious simplicity and wide usage, a penalized estimating equation based shrinkage estimation procedure is introduced, following the idea of [17] .

The rest of this article is organized as follows. In Section 2, the model, estimation procedure and statistical properties of the estimators are introduced. In Section 3, the practical computational issues are discussed and some numeric simulations and a real data analysis for the finite sample performance are illustrated in Section 4.

2. Estimation and Asymptotic Property

2.1. Penalized Estimating Equation

Let 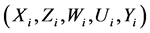be the observed data associated with the ith subject in a longitudinal study. We consider the partially linear varying coefficient mixed effect model (PLVCMeM)

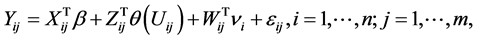(1)

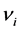where is a coefficient vector, is a 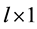vector of random effect with mean 0 and covariance matrix D, 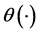is an unknown smoothing 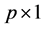function vector and 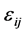is a random variable with mean 0 and variance.

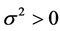Assume that 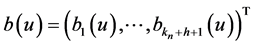is a set of B-spline basis functions of order 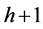with 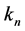quasi-uniform internal knots. Then, each 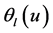can be expressed with a linear combination of normalized B-spline basis function 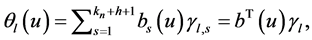where 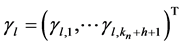is the spline coefficient vector. Therefore, with the given spline basis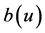, model (1) can be approximated as

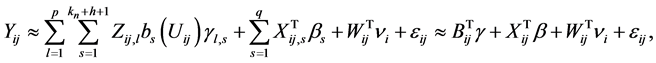(2)

where Hence, the estimators for and can be derived with the following weighted least square equation

(3)

where is the variance-covariance matrix.

A primary goal for (1) is to explore useful information for Z and X, it is important to select and estimate the nonzero coefficients in and nonzero functions in to enhance model prediction and interpretability. To achieve the simultaneous estimation and variable selection, a shrinkage penalty function is developed based on estimating equation with a regularization based shrinkage estimation being defined with the following penalized estimating equation, which is similarly introduced in [17] as

(4)

where. Alternatively, when denoting, it follows that

(5)

where is a penalty function used to penalize the coefficients of nonsignificant variables, is a tuning parameter.

Among many choices of the penalty function, the smoothly clipped and deviations (SCAD) penalty function is adopted as

(6)

where and, which is suggested by [10] . Since the SCAD penalty is a spline function on an interval near zero and constant outside, it can shrink small value of an estimation to zero while having no impact on the large one.

2.2. Estimators of the Variance Components

An efficient estimation for the parameters of interest in model (5) depends on estimators for the variance component, therefore a consistent estimators for them is required. Suppose that the variance covariance matrix for model (1) is

(7)

where represents a vector of ones and is the identity matrix. Model (7) is called a variance component model and is very popular in longitudinal analysis. See, for example, [3] [6] [9] and so on. Furthermore, let with Hence, it follows that a moment estimator for variance component of is derived as

(8)

where by the estimator and obtained from (3) without the weight, the residual is defined as

(9)

Therefore, the estimator for is defined as

(10)

2.3. Asymptotic Properties about the Estimators

In this section, we investigate the asymptotic behavior of the estimators for the parametric, nonparametric and variance component as well. Throughout the article, the following assumptions are needed to facilitate the technical details, although they may not be the weakest conditions. Let and be the true value of the corresponding parameters and.

(C1) For some, are rth continuously differentiable.

(C2) The density function f(u), which genernates the sequence of design points, is bounded away from 0 and infinity on [0, 1]. And assume that f(u) is continuously differentiable on (0, 1).

(C3) The number of measurements m is bounded.

(C4) For an, assume that, and

(C5) Let The eigenvalues of and are bounded away from infinity and zero for sufficiently large n.

Firstly, we present that the estimators given by (8) are asymptotic normal.

Theorem 1 Suppose that conditions (C1)?(C5) hold, then

(11)

where

To obtain the consistency and oracle property about the estimators, additional conditions are required as follows, which are similar to that used in [10] and [15] .

(C6) Let, then, as.

(C7) and where

Theorem 2 Under the conditions (C1)-(C7) and the number of knots Then,

i) (12)

ii) (13)

where, and r is defined in (C1).

Theorem 2 ensures the convergence rate of the weighted estimators for not only the parametric component, but also the nonparametric component. Furthermore, the following two theorems provide us with the oracle property of the consistent estimators.

Theorem 3 Under the conditions (C1)-(C7) and the number of knots

Let, and.If, and

as. Then, with probability tending to 1, and satisfy

i) (14)

ii) (15)

According to Remark 1 in [10] , the variable selection procedure can specify the model correctly and efficiently. Next theorem further shows us that under some conditions, the nonzero coefficient estimators of the parametric component have the same asymptotic distribution as that based on true model.

Let, and and be the true values of and, respectively. Therefore, the following theorem about the asymptotic distribution of the estimator is established.

Theorem 4 Under the conditions (C1)-(C7) and the number of knots Then

(16)

where is defined by (A.10) in Appendix.

3. Practical Computational Issues

Denote that and are the true and estimated covariance matrix within the ith subject. With a given initial value, we can refine the regularized estimators according to the following iterative algorithms.

Step 1. Calculate the estimator by the formula (10) with the given value.

Step 2. Solve the penalized estimators for the parametric and nonparametric component by the Equation (5) with the within-subject covariance matrix interpolated by the covariance matrix estimated in Step 1.

Step 3. Replace the estimator in Step 1 with the one in Step 2 and iterate between Step 1 and Step 2 until the convergence criterion is met. Consequently, the required estimator can be solved with this iterative procedure.

Remark 1. This modified penalized estimation procedure inherits the computational efficiency and sparsity of Lasso type solutions. And the computational details can be referred to [13] .

Although our theoretical results give technical conditions on and, in practice, these parameters is always chosen based on data to enhance the adaptive property. It follows that the cross validation method is used to choose the optimal and. However, in the real application, the parameter and is chosen by minimizing the following cross-validation score

(17)

where is the solution to the function (3) with the ith subject being deleted. Considering the character of the turning parameter, in practice, the turning parameter is used as and where and are the estimators of (3).

4. Empirical Study

We now use two examples to illustrate the superiority of the proposed weighted shrinkage estimation to that one without considering within-subject correlation.

Example 1. Consider a partially linear varying coefficient mixed effect model

(18)

where with, , and with and and other parametric and nonparametric component coefficients are zero. Moreover, it is further assumed that, and Meanwhile, denote that and ,where is set to be (2,0.5) and (1,0.5). It is assumed that the number of observed subject and repeated measurement within each subject are n = 50 and m = 3, 4, respectively.

To illustrate the estimation accuracy of the proposed method, we define generalized mean squared errors (GMSE) and the square root of average square error (RASE) to be

and (19)

And for the purpose of a intensive comparison, in addition to the proposed method in this article, two other estimation methods are also required, that are the “naive” approach based on the working independence method, and the “ideal” one based on the true within-subject covariance. And the estimator, obtained by the “naive” approach, the proposed method in this article and the “ideal” approach, are denoted to be, and, respectively. During the simulations, it is assumed that “C” and “I” means the average number of the zero coefficients being correctly set to zero and the average number of the nonzero coefficients being incorrectly set to zero, respectively.

The results about variable selection, based on 100 replications, are included in Table 1. Table 1 shows that the proposed method can select the true model quite well and leads to smaller GMSE and RASE values. Table 2 reports a satisfactory estimation for the variance component. As the sample increase, the performance becomes better.

Secondly, the variance, bias and mean square error of the estimators for the nonzero parameters, denoted to be “V”, “Bias” and “MSE”, are listed in Table 3. From Table 3, all the three methods can obtain consistent estimators with small bias. Moreover, the values of “V” and “MSE” also argue that the newly proposed method and the “ideal” method can derive a more efficient estimator than the “naive” method does. What’s more, the asymptotic normality of the estimators for the parametric component is shown with Quantile-Quantile plot in Figure 1.

Finally, in Figure 2, all of the curves, estimated by all the three methods, fit the true nonparametric curve well. However, their 95% confidence intervals have different interval length, with the proposed method in this article and the “ideal” method showing a similar and smaller length. All these scenarios indicate a great improvement of the estimation with the proposed method in this article.

Example 2. To illustrate the effectiveness of the proposed estimation procedure, we shall apply it to the analysis of a longitudinal AIDS data set, which is reported by [18] and comprises HIV status of 283 homosexual males who were infected with HIV during a follow-up period between 1984 and 1991. The focus in this application is to probe into the trend of the mean CD4 percentage depletion over time and evaluate the effects of cigarette smoking, preHIV infection CD4 percentage and age at infection on the mean CD4 percentage after infection.

For the jth measurement of the ith subject, let be the mean CD4 percentage, be the time in years after HIV infection, be the centered preCD4 percentage and

be the centered age at HIV infection and Let be the smoking status taking a value of 1 or 0. Hence, assume the following model

(20)

where the baseline of CD4 percentage is used to represent the mean CD4 percentage of t years after the infection. The random effect, representing the within-subject correlation, is also included in the assumed model.

By the analysis, there are two variables and with nonzero estimators, which indicate the significant effect on the response variable. Other variables’ coefficients are zero and have no significant effect. Moreover, the estimated curve in Figure 3 shows the trend of the mean CD4 percentage depletion over time.

5. Conclusion and Discussion

This article considered an efficient shrinkage estimation for the partially linear varying coefficient models with random effect. Variance component model was employed to take within subject correlation into consideration. Some asymptotic properties, such as convergence rate, consistency and oracle property, were established. Moreover, the effectiveness was further illustrated by a real data analysis. As a more ambitious goal, we would try to investigate the performance of variable selection issue for mixed effect

model under a more general within-subject covariance matrix.

Acknowledgements

This work was partially supported by the National Statistical Science Research Project of China [Grant No. 2014LZ14 and 2015LZ27] and the Yancheng Teachers’ Professor and Doctors’ Research Project [Grant No. 14YSYJB0108].

Cite this paper

Li, W.B. (2016) Efficient Shrinkage Estimation about the Partially Linear Varying Coefficient Model with Random Effect for Longitudinal Data. Open Journal of Statistics, 6, 862-872. http://dx.doi.org/10.4236/ojs.2016.65071

References

Appendix

Supplementary material related to this article can be asked for by email.