Open Journal of Statistics
Vol.05 No.05(2015), Article ID:58914,9 pages
10.4236/ojs.2015.55048
Fluctuation-Model-Based Discrete Probability Estimation for Small Samples
Takashi Isozaki
Sony Computer Science Laboratories, Inc., Tokyo, Japan
Email: isozaki@csl.sony.co.jp
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 July 2015; accepted 17 August 2015; published 20 August 2015
ABSTRACT
A robust method is proposed for estimating discrete probability functions for small samples. The proposed approach introduces and minimizes a parameterized objective function that is analogous to free energy functions in statistical physics. A key feature of the method is a model of the parameter that controls the trade-off between likelihood and robustness in response to the degree of fluctuation. The method thus does not require the value of the parameter to be manually selected. It is proved that the estimator approaches the maximum likelihood estimator at the asymptotic limit. The effectiveness of the method in terms of robustness is demonstrated by experimental studies on point estimation for probability distributions with various entropies.
Keywords:
Probability Estimation, Fluctuation Models, Helmholtz Free Energy, Canonical Distributions

1. Introduction
For categorical observational data analysis, it is often necessary to deal with multivariate systems since variables of such data generally depend on each other. Highly predictive statistical inference requires parameters that achieve low-entropy, so it is preferable to use data of many variables because the following relationship in Shannon entropies H of random variables X and Y holds if X and Y depend on each other: 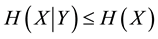 [1] , where
[1] , where 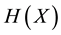 denotes Shannon entropy of X and
denotes Shannon entropy of X and 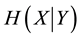 denotes the conditional entropy of X given Y. These are respectively defined with marginal, joint, and conditional probability mass functions P as follows [1] :
denotes the conditional entropy of X given Y. These are respectively defined with marginal, joint, and conditional probability mass functions P as follows [1] :
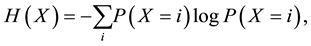
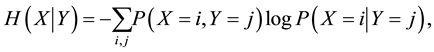
where i and j are indices of discrete states of X and Y. When we estimate probabilities in discrete probabilistic models with many-variables (e.g., Markov network and Bayesian network models [2] ), statistical estimation of conditional and joint probabilities often needs exponentially large data because of the combinatorial explosion of binding events in variables. Therefore, the models are often inferred from insufficient data. The maximum likelihood (ML) method provides an estimated probability function, which of X with k discrete states is expressed by
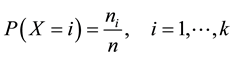

where n and 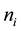 respectively denote a sample size and the frequency of occurrences in i state. The estimated probability is correct in the large sample limit. However, the ML methods suffer from short size data, and few robust methods have been investigated for such data in estimation of discrete probability functions as far as we know, although many robust methods for outliers such as M-estimators have been developed [3] [4] in para- metric continuous distributions. The maximum entropy method [5] , which may be applied to small datasets, was originally appropriate for data with missing information.
respectively denote a sample size and the frequency of occurrences in i state. The estimated probability is correct in the large sample limit. However, the ML methods suffer from short size data, and few robust methods have been investigated for such data in estimation of discrete probability functions as far as we know, although many robust methods for outliers such as M-estimators have been developed [3] [4] in para- metric continuous distributions. The maximum entropy method [5] , which may be applied to small datasets, was originally appropriate for data with missing information.
In the present study, a new robust method is proposed for estimating discrete probability functions for small samples. The method uses a parameterized objective function based on Kullback-Leibler divergence [6] and Shannon entropy. The function has a similar form to the Helmholtz free energy function that appears in statistical physics [7] [8] . A key feature of the method is a model of the parameter that controls the trade-off between likelihood and robustness in response to the degree of data fluctuation. The method thus does not require the value of the parameter to be manually selected. This model is a modification of a preceding work [9] , in which the parameter is represented by an artificial model containing a free hyperparameter.
In the domain of machine learning, although several methods slightly similar to ours have been proposed [10] - [14] , there is a critical distinction between these methods and ours. Many studies that have applied free energy to statistical inference have not included the similar trade-off parameter or have treated it as a fixed value, a manually controlled parameter, or a free parameter. Regarding the existing methods, we thus consider that the potentials of free-energy-like functions have not been well extracted. Other similar methods have been developed in the context of robust estimation for outliers, in which a free parameter is introduced in an analogous fashion [3] [15] [16] . However, the problem of how to determine the value of the free parameters remains.
This paper is organized as follows. In the next section, an objective function with parameter 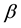 is introduced for robust estimation, and then probability functions obtained by the proposed method are shown to be formally equivalent to the canonical distributions that appear in statistical physics. In Section 3, a new representation of
is introduced for robust estimation, and then probability functions obtained by the proposed method are shown to be formally equivalent to the canonical distributions that appear in statistical physics. In Section 3, a new representation of 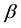 is presented as a data-fluctuation-model, and the preferable asymptotic property of
is presented as a data-fluctuation-model, and the preferable asymptotic property of  is proved. In Section 4, some characteristic properties among quantities used in the proposed method are provided. In Section 5, we perform experiments using the proposed probability estimation method. In Section 6, conclusions regarding the estimation method are given.
is proved. In Section 4, some characteristic properties among quantities used in the proposed method are provided. In Section 5, we perform experiments using the proposed probability estimation method. In Section 6, conclusions regarding the estimation method are given.
2. Probability Estimation with Parameter β
Note that in this paper a capital letter (such as X) denotes a random discrete variable, a non-capital letter (such as x) denotes the special state of that variable, a bold capital letter (such as ) denotes a set of variables, and a bold non-capital letter (such as
) denotes a set of variables, and a bold non-capital letter (such as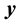 ) denotes configurations of that set.
) denotes configurations of that set.
To construct a method for estimating finite-discrete-probability distributions of random variable X from sample set of finite size n, the following quantities are defined. 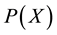 denotes a discrete-probability function estimated by a proposed method that is described below. A function of X is defined as
denotes a discrete-probability function estimated by a proposed method that is described below. A function of X is defined as 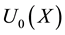 on the basis of the Kullback--Leibler (KL) divergence [6] between empirical functions and
on the basis of the Kullback--Leibler (KL) divergence [6] between empirical functions and 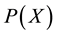 as follows:
as follows:

where 




where 

as


and 





and

where




In addition, the following quantity 






The estimator of probability functions, 



where 


where 

For estimating conditional and joint-probability functions, conditional entropy

are used. 

The formula for estimating conditional probabilities is therefore obtained by using the conditional entropy and KL divergence and 

Joint probability can be calculated by using Equations (8) and (10) and the definite relation 
3. Model of β












where 




Then, 



where




distribution 







Objective function F is rewritten in the same form as that in statistical mechanics as follows:

where Z is the partition function, which is a similar function well known in statistical mechanics, defined for single or multivariate probabilities as

and for conditional probabilities as

A significant feature of 
Lemma 1.






Proof.

Because 









Theorem 1. At the asymptotic limit (i.e., large sample limit), 



Proof. According to Lemma 1, 
















for 







(18), while 

According to Theorem 1, the more data are obtained, the more 



The role of 

where 


ATML has an analogy with statistical physics, since the canonical distribution for the estimator is obtained from Equation (8). Actually, U, H, 


ATML may seem analogous to Jaynes’ maximum entropy (ME) methods [5] , which are well known as least- biased inference methods. However, the constraints on which ME methods are based may not be reliable for small samples and thus may be biased, although this kind of bias is not usually considered. On the other hand, ATML is thus designed so that even the bias can be corrected by using parameter
4. Characteristic Properties of ATML
The canonical distribution expressed as Equation (8) can provide some characteristic properties of ATML, which are similar to those in statistical physics. The following notations are defined for later convenience. Pro- bability mass functions that are estimated by ATML, denoted by



In statistical physics, (inverted) temperature 

If the canonical distribution of
Lemma 2. 

Proof. Since probability mass function 

Theorem 2. Equation (20) is automatically satisfied under the MFE condition.
Proof. Partially differentiating both sides of Equation (21) with respect to U gives


It follows that

In the same way, it can be proved that



In regard to 
Equation (24) is therefore proved.
Fisher information 


where f is the likelihood function. We define tempered Fisher information 



The tempered Fisher information is therefore identical to Equation (24).
It is noteworthy that ATML has other mathematical similarities with statistical physics. That is, the same relationships that appear in statistical physics listed as follows hold.
・ The following relation is easily derived from the definition of partition function Z:

・ The following relation, known as the Gibbs-Helmholtz relation, is derived from Equations (13) and (27) as

・ The following relation is simply obtained from Equations (5) and (28) as

・ The tempered Fisher information is represented by the second-order differential of the partition function for 

5. Examples
Numerical experiments are performed to demonstrate the robustness of ATML for small samples, in comparison with the ML and ME methods [5] .
X is assumed to have three internal states and four probability mass functions with a variety of entropies denoted as 
1.
2.
3.
4.
Data from each function was sampled, and probabilities were estimated from given data sets with various data sizes. According to convention, averaged outputs 

estimated probabilities were compared by using KL divergence as a metric with the following form:

where 

The KL divergences are shown in Figure 1, where they are averaged values from 100 samples at each sample size from identical distributions. It can be seen that the ML estimators are inferior to ATML due to overfitting, except for the distribution having very small entropy. Even the degree of superiority of the ML estimation in (d) is relatively smaller than that of inferiority in other distributions. The ME estimators showed the opposite be- haviors to those by the ML estimators, and showed some relatively poor results in large-sample regions. ML methods tend to fit data and can thus more accurately estimate distributions with very low entropies than others in small-sample cases. For example, if a true entropy equals zero, the ML method can estimate the exact true
Figure 1. KL divergences between true probability mass functions and probability mass functions estimated by using ML, ATML, and ME. The horizontal axes denote sample sizes. H denotes Shannon entropy in natural logarithms. (a) H = 1:07; (b) H = 0:841; (c) H = 0:498; (d) H = 0:0621.
distribution from only one sample. On the other hand, ME methods tend to increase entropies and can thereby accurately estimate distributions with high entropies close to the uniform distributions. Hence, the ML method tends to overfit data, and the ME method tends to underfit data in the view of misestimation. Even so, ATML showed relative stability in terms of both sample sizes and distributions. This result indicates the effectiveness of ATML as a probability estimation method.
6. Conclusion
A robust method for estimating discrete probability functions, called “adaptively tempered maximum likelihood” method (ATML for short), is proposed. The estimators obtained in this method minimize a parameterized objective function similar to Helmholtz free energies that appear in statistical physics. The key feature of the proposed method is a model of the parameter as a fluctuation of finite size data. The parameter that is modeled plays an important role in determining the appropriate trade-off between likelihood and robustness in response to the degree of the fluctuations. ATML does thereby not require manually selecting the value of the parameter. It is also proved that the obtained estimator approaches the maximum likelihood estimator at the asymptotic limit. The effectiveness of ATML in terms of robustness was demonstrated by experimental studies on point estimation for probability distributions with various entropies.
Acknowledgements
The author thanks Mario Tokoro and Hiroaki Kitano of Sony Computer Science Laboratories, Inc. for their support as well as Te Sun Han, Hiroshi Nagaoka, Tomohiro Ogawa and Jun Suzuki of the University of Electro- Communications for their valuable comments and discussions.
Cite this paper
TakashiIsozaki, (2015) Fluctuation-Model-Based Discrete Probability Estimation for Small Samples. Open Journal of Statistics,05,465-474. doi: 10.4236/ojs.2015.55048
References
- 1. Shannon, C.E. (1948) A Mathematical Theory of Communication. Bell Systems Technical Journal, 27, 379-423, 623-656.
- 2. Pearl, J. (1988) Probabilistic Reasoning in Intelligent Systems. Morgan Kaufmann, San Mateo, CA.
- 3. Basu, A., Harris, I.R., Hjort, N.L. and Jones, M.C. (1998) Robust and Efficient Estimation by Minimising a Density Power Divergence. Biometrika, 85, 549-559.
http://dx.doi.org/10.1093/biomet/85.3.549 - 4. Beran, R. (1977) Minimum Hellinger Distance Estimates for Parametric Models. Annals of Statistics, 5, 445-463.
http://dx.doi.org/10.1214/aos/1176343842 - 5. Jaynes, E.T. (1957) Information Theory and Statistical Mechanics. Physical Review, 106, 620-630.
http://dx.doi.org/10.1103/PhysRev.106.620 - 6. Kullback, S. and Leibler, R.A. (1951) On Information and Sufficiency. Annals of Mathematical Statistics, 22, 79-86.
http://dx.doi.org/10.1214/aoms/1177729694 - 7. Callen, H.B. (1985) Thermodynamics and an Introduction to Thermostatistics. 2nd Edition, John Wiley & Sons, Hoboken, NJ.
- 8. Kittel, C. and Kroemer, H. (1980) Thermal Physics. W. H. Freeman, San Francisco, CA.
- 9. Isozaki, T., Kato, N. and Ueno, M. (2009) “Data Temperature” in Minimum Free Energies for Parameter Learning of Bayesian Networks. International Journal on Artificial Intelligence Tools, 18, 653-671.
http://dx.doi.org/10.1142/S0218213009000342 - 10. Hofmann, T. (1999) Probabilistic Latent Semantic Analysis. Proceedings of Conference on Uncertainty in Artificial Intelligence (UAI-99), Stockholm, 30 July-1 August 1999, 289-296.
- 11. LeCun, Y. and Huang, F.J. (2005) Loss Functions for Discriminative Training of Energy-Based Models. Proceedings of International Workshop on Artificial Intelligence and Statistics (AISTATS-05), Barbados, 6-8 January 2005, 206-213.
- 12. Pereira, F., Tishby, N. and Lee, L. (1993) Distributional Clustering of English Words. In: Proceedings of Annual Meeting on Association for Computational Linguistics (ACL-93), Association for Computational Linguistics, Stroudsburg, 183-190.
http://dx.doi.org/10.3115/981574.981598 - 13. Ueda, N. and Nakano, R. (1995) Deterministic Annealing Variant of the EM Algorithm. Proceedings of Advances in Neural Information Processing Systems 7 (NIPS 7), Denver, 29 November-1 December 1994, 545-552.
- 14. Watanabe, K., Shiga, M. and Watanabe, S. (2009) Upper Bound for Variational Free Energy of Bayesian Networks. Machine Learning, 75, 199-215.
http://dx.doi.org/10.1007/s10994-008-5099-x - 15. Jones, M.C., Hjort, N.L., Harris, I.R. and Basu, A. (2001) A Comparison of Related Density-Based Minimum Divergence Estimators. Biometrika, 88, 865-873.
http://dx.doi.org/10.1093/biomet/88.3.865 - 16. Windham, M.P. (1995) Robustifying Model Fitting. Journal of the Royal Statistical Society B, 57, 599-609.
- 17. Pöschel, T., Ebeling, W., Frömmel, C. and Ramírez, R. (2003) Correction Algorithm for Finite Sample Statistics. The European Physical Journal E, 12, 531-541.
http://dx.doi.org/10.1140/epje/e2004-00025-4









