Open Journal of Geology
Vol.05 No.05(2015), Article ID:56667,15 pages
10.4236/ojg.2015.55032
Slope Year for the U-Pb Dating Method and Its Applications
Jie Yuan
Key Laboratory of Earth and Planetary Physics, Institute of Geology and Geophysics, Chinese Academy of Science, Beijing, China
Email: yuanjie@mail.iggcas.ac.cn
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 April 2015; accepted 23 May 2015; published 26 May 2015
ABSTRACT
The slope year tslope for the U-Pb dating method is given as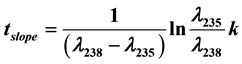 , where λ238 and λ235 are the decay constants for 238U and 235U, respectively, and k is the slope of the tangent line at a point on either the Concordia or Discordia line. These two lines are determined by the initial 206(7)Pbi concentrations in minerals. If
, where λ238 and λ235 are the decay constants for 238U and 235U, respectively, and k is the slope of the tangent line at a point on either the Concordia or Discordia line. These two lines are determined by the initial 206(7)Pbi concentrations in minerals. If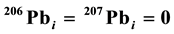 , the line is the Concordia. However, if
, the line is the Concordia. However, if 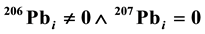 (
(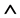 is the logical operator “and”, also known as the logical conjunction),
is the logical operator “and”, also known as the logical conjunction),  or
or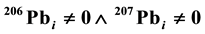 , the line is Discordia. The Concordia line is of the form
, the line is Discordia. The Concordia line is of the form 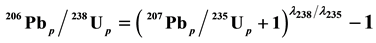 (where p stands for the present), while the Discordia line has the form
(where p stands for the present), while the Discordia line has the form 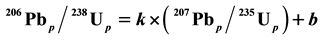 (where k and b are the slope and intercept of the straight line, respectively).
(where k and b are the slope and intercept of the straight line, respectively).
Keywords:
Slope Year, U-Pb Dating, Zircon, Mass Spectrum, Isotope, Initial Pb Isotope Concentration

1. Introduction
In nature, uranium has three radioactive isotopes: 238U(99.2743%), 235U(0.7200%) and 234U(0.0057%) [1] [2] . The former two isotopes decay in the forms:
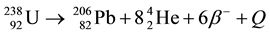
and ,
,
where Q is the heat, β denotes the beta decay and He stands for the element Helium. The decay constants λ for 238U and 235U are 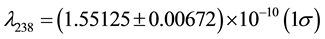 a−1 and
a−1 and  a−1, respectively [2] -[4] .
a−1, respectively [2] -[4] .
These nuclear reactions occur in host minerals, such as zircon (ZrSiO4), and are the basis of the U-Pb dating method in geology [5] -[8] . In a mineral, Pb and U isotopes obey the exponential decay law:
 (1)
(1)
and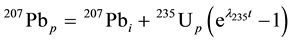 , (2)
, (2)
where the subscripts i and p represent the initial measurement time and the present, respectively, and t is the age of the mineral [1] [6] .
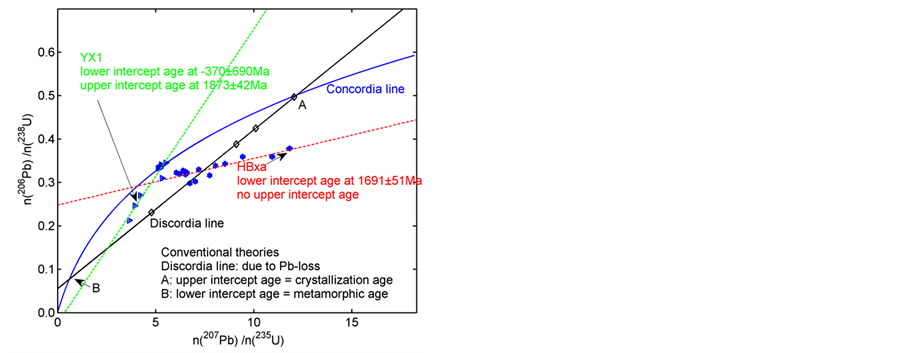
The coordinates n(206Pbp)/n(238Up) (n, the number of isotopes in the bracket) as the ordinate and n(207Pbp)/ n(235Up) ratios as the abscissa form the Pb/U ratio diagram (Figure 1). Samples formed t years ago plot on either the Concordia or Discordia lines [9] -[12] . For instance, the classical Discordia line was discovered by Ahrens (1955) in Zimbabwe. Equation (1) divided by 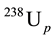 is n(206Pbp)/n(238Up):
is n(206Pbp)/n(238Up):
 . (3)
. (3)
Similarly for n(207Pbp)/n(235Up), we have

from Equation (2).
To interpret the Discordia line, conventional theories have proposed: 1) this line was caused by Pb loss or U gain after formation of the host mineral [9] [11] -[17] , 2) the upper intersection of the Discordia and Concordia lines represents the crystallization age of the mineral [12] and 3) the lower intersection of the Discordia and Concordia lines represents the metamorphic age of the mineral [14] .
However, previous theories are not tenable when used in the following cases:
1) the lower intercept point is negative or
2) no upper intercept point exists.
For instance, in Zheng et al. (2012) (Figure 1), all zircons in YX1 from Yingxian lamproites were found to be discordant and yielded a lower intercept age of −370 ± 690 Ma. According to conventional theories, this age indicates that the samples will experience a metamorphic process in a distant age. In addition, in Zheng et al. (2012), all zircons in HBxa from Hebi basalt are also discordant, but yield no upper intercept age. According to conventional theories, these data indicate that the samples did not crystallize until the present. Apparently, the explanations do not conform to the objective facts: the samples are in front of scientists now. New studies should thus focus on resolving these discrepancies.
Herein, the slope years tslopes for the U-Pb dating method for the Concordia and Discordia lines are presented, and a method for estimating values for tslope from the experimental data is proposed. In addition, four examples are presented to illustrate the application of the proposed method.
2. Methodology
2.1. Basic Assumptions
In this study, the basic assumptions for the U-Pb dating method included the following:
a) The decay constants λ238 and λ235 are precisely determined. For instance, the decay constants in Jaffey et al. (1971) are of good quality and widely accepted. The number of citations of this paper is greater than 1200 (data from Web of Science);
b) Host minerals are not influenced by chemical reactions after formation. The minerals included apatite [18] [19] , baddeleyite [20] -[25] , monazite [26] -[33] , tantalite [34] -[38] , titanite [39] -[41] , uraninite [42] [43] and zircon [44] [45] , etc.;
Figure 1. Pb/U ratio diagram. This diagram shows the predicament for conventional theories. The Concordia (blue, colour for online version) and classical Discordia (black) for Zimbabwe samples (black diamond points) (Ahrens, 1955) are illustrated. This Discordia and Concordia intercept at A and B, for which the meanings in conventional theories are shown in the lower-right corner. Two counter-examples to traditional theories are also shown: HBxa (hexagon points and red Discordia, Zheng et al. (2012)) and YX1 (right triangle points and green Discordia, Zheng et al. (2012)). See discussions in text.
c) Present 206(7)Pbp and 235(8)Up isotope concentrations in host minerals can be precisely measured using mass spectrometry (MS). Such MS instruments include sensitive high mass-resolution ion microprobe (SHRIMP) [46] [47] , LaserProbe-inductively coupled plasma mass spectrometry (LP-ICPMS) [48] and Cameca IMS-series [44] [49] , etc.
2.2. Slope k and Slope Year Tslope
In mathematics, the variance on the ordinate is a function of the variance on the abscissa [50] . Therefore, n(206Pbp)/n(238Up) is a function of n(207Pbp)/n(235Up) in the Pb/U diagram (Figure 2):

The theoretical expressions for this function under different conditions are given in Section 2.4.
Next, the slope k of the tangent line at point A on the general curve of Equation (5) was determined. The partial derivative of 

Similarly, we have

from Equation (4). Equation (6) divided by Equation (7) gives

Figure 2. Pb/U ratio diagram. The general curve (in blue) for 
In this equation, the second part is the definition of the slope of the tangent line [50] :

This equation indicates that if t is determined, the value of k is a constant (Table 1) since t ≥ 0, 0 < k ≤ 0.1575. In addition, the slope monotonically decreases with increasing time t (Figure 3).
If k is determined (see Section 2.6), the slope year is given by rewriting Equation (9):

2.3. Initial 206(7)Pbi Concentrations in Minerals
If the values for tslope, 206(7)Pbp and 235(8)Up are known, the initial 206(7)Pbi concentrations in minerals can be determined using the following:

and
which are derived from Equations (1) and (2). Clearly, the concentrations are greater than or equal to zero:
2.4. Mathematical Expressions for the Concordia and Discordia Lines
The initial 206(7)Pbi isotope concentrations determine the mathematical expressions for the general graph in Figure 2. This relationship can be demonstrated using assumed samples formed at the same time t with specific initial conditions. Assume there are three samples (1, 2 and 3, Figure 4(a)) with

and an additional three samples (4, 5 and 6, Figure 4(b)) with
Figure 3. Plot of the slope k versus time t.

Figure 4. Histories of Pb/U ratios (blue circle) for different samples on (a) Concordia and (b) Discordia. The red arrows indicate the direction of the evolution of each ratio.
Table 1. Values of the slope for specific years.
a, calculated from Equation (9)

The mathematical expressions are given by solving the first-order differential Equation (9) using Equations (3) and (4):

The solution to this equation is different for each set of samples.
a) For samples 1, 2 and 3, rewriting Equation (15) using Equation (13) gives

The general solution of Equation (16) is

Since the concentrations of 


or

which is the expression for the Concordia line.
b) For samples 4, 5 and 6, because of the existence of the variances in 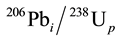

This difficulty can be overcome in the following manner. Consider a geological body (containing samples 4, 5 and 6) with continuous 206Pbi, 207Pbi, 




Since k is a constant when t is given (Table 1), the solution to this equation is

where k and b are the slope and intercept of the line, respectively. This equation shows that the general curve in Figure 2 is a straight line, i.e. the Discordia line.
Equation (21) is consistent with the initial condition (Equation (14)). If k = 0.15751 (at t = 0) is applied:

This equation indicates that 1) in the geological system, 206Pbi/238Ui monotonically increases with increasing 207Pbi/235Ui from samples 4 to 5 to 6 (Figure 4(b)) and 2) these two ratios for the three samples cannot simultaneously be zero.
2.5. Histories of Pb/U Ratios on the Concordia and Discordia Lines
The 

a) samples 1, 2 and 3 (Figure 4(a)), for which when t = 0, the 
b) samples 4, 5 and 6 (Figure 4(b)), for which when t = 0 the 

2.6. Methods for Determining k from Experimental Data
For n 

a) If the n data points plot on the Concordia line (Figure 4(a)), using Equation (19), the slope of the ith data point is

where

b) If the n data points plot on the Discordia line (Figure 4(b)), the slope can be determined using the least squares method [51] . This method gives a linear function for the points:

where

and


2.7. Error Propagation
For a function

where


According to Equation (27), the standard error for tslope (Equation (10)) is

or

where 



a) For concordant data, the standard error of the ith slope (Equation (23)) is

and the standard error of the mean slope (Equation (24)) is

b) For discordant data, the standard error of k in Equation (26) is

See proofs of this equation in Appendix A.
According to Equation (27), the standard error for 206(207)Pbi (Equations (11) and (12)) is

where m and n stand for 206(7) and 235(8) respectively, 




3. Applications
To demonstrate the validity of our work, four examples are illustrated (Table 2 and Figure 5). Table 2 includes original Pb/U isotope ratios from the published literature along with the slope years (i.e. U-Pb ages) when the samples were formed.
The first example comes from Qinghu granite in the Nanling Range, South China [44] . The Pb/U ratios in this granite are the concordant type (Figure 5(a)) [44] . The slope and slope year were calculated using Equations (24) and (10), respectively, and found to be kConcordia = 0.13792 ± 0.00025 and tslope = 160 ± 2 Ma (Table 2), which are in good agreement with values reported by Li et al., 2009.


Figure 5. Present slope years (with 1σ error) for (a) Qinghu granite, (b) a Zimbabwe uranium deposit, (c) Yingxian amphibolites and (d) Hebi amphibolites. All data points except Zimbabwe are plotted with 1σ error bars. The norms of the residuals (R2) for the least squares fits are illustrated, and the slopes (with 1σ errors) are given. In (a), the red diamond indicates the mean value for all the measured data and the tangent line at this point coincides with the Concordia line.
The k and tslope values for the three discordant examples described in the introduction were also calculated using Equations (26) and (10), respectively. For the Zimbabwe uranium deposit (Figure 5(b)), the slope was kDiscordia = 0.03950 ± 0.00178 and slope year was tslope = 1668 ± 55 Ma. For amphibolites in the Yingxian lamproite (YX1, Figure 5(c)), the slope was kDiscordia = 0.06779 ± 0.00564 and slope year was tslope = 1016 ± 100 Ma. For Hebi amphibolites (HBxa, Figure 5(d)), the slope was kDiscordia = 0.010734 ± 0.00196 and slope year was tslope = 3237 ± 220 Ma.
4. Conclusion
A method for determining the slope year for the U-Pb dating method and initial 206(7)Pb concentrations in samples was described. It was also found that if no 206(7)Pb isotopes are initially present in minerals, the Pb/U ratios plot on the Concordia line. On the other hand, if 206(7)Pb isotopes are initially present in minerals, the Pb/U ratios plot on the Discordia line. Therefore, the Discordia line is not the result of Pb loss or U gain. Furthermore, methods for determining the slope year using experimental data were also proposed and applied to data on four samples previously described in the literature. These results demonstrate that our approach is useful for geological research.
Table 2. Values for 206Pb/238U, 207Pb/235U, the slope (k) and the slope year (tslope) of zircons in different geological bodies. The Pb/U isotope ratios in the Qinghu granite (07QH-1), a Zimbabwe uranium deposit, Yingxian amphibolites (YX1) and Hebi amphibolites (HBxa) are taken from Li et al. (2009), Ahrens, (1955), Zheng et al. (2012) and Zheng et al. (2012), respectively.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant Nos. 41303047, 90914010 and 41020134003).
References
- Rutherford, E. and Soddy, F. (1903) The Radioactivity of Uranium. Philosophical Magazine, 5, 25-30, 441-445.
- Audi, G., Bersillon, O., Blachot, J. and Wapstra, A.H. (2003) The Nubase Evaluation of Nuclear and Decay Properties. Nuclear Physics A, 729, 3-128. http://dx.doi.org/10.1016/j.nuclphysa.2003.11.001
- Jaffey, A.H., Flynn, K.F., Glendenin, L.E., Bentley, W.C. and Essling, A.M. (1971) Precision Measurement of Half- Lives and Specific Activities of 235U and 238U. Physical Review C, 4, 1889-1906. http://dx.doi.org/10.1103/PhysRevC.4.1889
- Pomme, S., Garcia-Torano, E., Sibbens, G., Richter, S., Wellum, R., Stolarz, A., et al. (2008) U-234/U-235 Activity Ratios as a Probe for the U-238/U-235 Half-Life Ratio. Journal of Radioanalytical and Nuclear Chemistry, 277, 207- 210. http://dx.doi.org/10.1007/s10967-008-0731-6
- Baker, T., Perkins, C., Blake, K.L. and Williams, P.J. (2001) Radiogenic and Stable Isotope Constraints on the Genesis of the Eloise Cu-Au Deposits, Cloncurry District, Northwest Queensland. Economic Geology, 96, 723-742. http://dx.doi.org/10.2113/96.4.723
- Muller, R. (1996) Radiogenic Isotope Geology. Physics Today, 49, 60. http://dx.doi.org/10.1063/1.2807660
- Panneerselvam, K., Macfarlane, A.W. and Salters, V.J.M. (2012) Reconnaissance Lead Isotope Characteristics of the Blackbird Deposit: Implications for the Age and Origin of Cobalt-Copper Mineralization in the Idaho Cobalt Belt, United States. Economic Geology, 107, 1177-1188. http://dx.doi.org/10.2113/econgeo.107.6.1177
- Solomon, M., Gemmell, J.B. and Zaw, K. (2004) Nature and Origin of the Fluids Responsible for Forming the Hellyer Zn-Pb-Cu, Volcanic-Hosted Massive Sulphide Deposit, Tasmania, Using Fluid Inclusions, and Stable and Radiogenic Isotopes. Ore Geology Reviews, 25, 89-124. http://dx.doi.org/10.1016/j.oregeorev.2003.11.001
- Ahrens, L.H. (1955) Implications of the Rhodesia Age Pattern. Geochimica et Cosmochimica Acta, 8, 1-15. http://dx.doi.org/10.1016/0016-7037(55)90013-2
- Mezger, K. and Krogstad, E.J. (1997) Interpretation of Discordant U-Pb Zircon Ages: An Evaluation. Journal of Metamorphic Geology, 15, 127-140. http://dx.doi.org/10.1111/j.1525-1314.1997.00008.x
- Tilton, G.R. (1960) Volume Diffusion as a Mechanism for Discordant Lead Ages. Journal of Geophysical Research, 65, 2933-2945. http://dx.doi.org/10.1029/JZ065i009p02933
- Wetherill, G.W. (1956) An Interpretation of the Rhodesia and Witwatersrand Age Patterns. Geochimica et Cosmochi- mica Acta, 9, 290-292. http://dx.doi.org/10.1016/0016-7037(56)90029-1
- Goldich, S.S. and Fischer, L.B. (1986) Air-Abrasion Experiments in U-Pb Dating of Zircon. Chemical Geology, 58, 195-215. http://dx.doi.org/10.1016/0168-9622(86)90010-2
- Goldrich, S.S. and Mudrey, M.G. (1972) Dilatancy Model for Discordant U-Pb Zircon Ages. In: Tugarinov, A.I., Ed., Contributions to Recent Geochemistry and Analytical Chemistry, Nauka Publishing Office, Moscow, 415-418.
- Holmes, A. (1954) The Oldest Dated Minerals of the Rhodesian Shield. Nature, 173, 612-614. http://dx.doi.org/10.1038/173612a0
- Silver, L.T. and Deutsch, S. (1961) Uranium-Lead Method on Zircons. Annals of the New York Academy of Sciences, 91, 279-283.
- Wasserburg, G.J. (1963) Diffusion Processes in Lead-Uranium Systems. Journal of Geophysical Research, 68, 4823- 4846.
- Chew, D.M., Sylvester, P.J. and Tubrett, M.N. (2011) U-Pb and Th-Pb Dating of Apatite by LA-ICPMS. Chemical Ge- ology, 280, 200-216. http://dx.doi.org/10.1016/j.chemgeo.2010.11.010
- Thomson, S.N., Gehrels, G.E., Ruiz, J. and Buchwaldt, R. (2012) Routine Low-Damage Apatite U-Pb Dating Using Laser Ablation-Multicollector-ICPMS. Geochemistry, Geophysics, Geosystems, 13, 1. http://dx.doi.org/10.1029/2011GC003928
- Allibon, J., Ovtcharova, M., Bussy, F., Cosca, M., Schaltegger, U., Bussien, D., et al. (2011) Lifetime of an Ocean Island Volcano Feeder Zone: Constraints from U-Pb Dating on Coexisting Zircon and Baddeleyite, and 40AR/39AR Age Determinations, Fuerteventura, Canary Islandssp. Canadian Journal of Earth Sciences, 48, 567-592. http://dx.doi.org/10.1139/E10-032
- Bayanova, T.B. and Yakovenchuk, V.N. (1994) U-Pb Dating of Baddeleyite and Zircon from Imandrites on the Kola Peninsula. Doklady Earth science sections, 323, 147-150.
- de Assis Janasi, V., de Freitas, V.A. and Heaman, L.H. (2011) The Onset of Flood Basalt Volcanism, Northern Parana Basin, Brazil: A Precise U-Pb Baddeleyite/Zircon Age for a Chapeco-Type Dacite. Earth and Planetary Science Letters, 302, 147-153. http://dx.doi.org/10.1016/j.epsl.2010.12.005
- Li, Q.-L., Li, X.-H., Liu, Y., Tang, G.-Q., Yang, J.-H. and Zhu, W.-G. (2010) Precise U-Pb and Pb-Pb Dating of Phanerozoic Baddeleyite by SIMS with Oxygen Flooding Technique. Journal of Analytical Atomic Spectrometry, 25, 1107- 1113. http://dx.doi.org/10.1039/b923444f
- Soderlund, U. (2006) U-Pb Baddeleyite Ages of Meso- and Neoproterozoic Dykes and Sills in Central Fennoscandia: A Review. 5th International Dyke Conference: Dyke Swarms―Time Markers of Crustal Evolution, IDC-5. Rovaniemi, 31 July 2005-3 August 2005, 75-84.
- Wahlgren, C.H., Heaman, L.M., Kamo, S. and Ingvald, E. (1996) U-Pb Baddeleyite Dating of Dolerite Dykes in the Eastern Part of the Sveconorwegian Orogen, South-Central Sweden. Precambrian Research, 79, 227-237. http://dx.doi.org/10.1016/0301-9268(95)00094-1
- Aleinikoff, J.N., Lack, J.F.S., Lund, K., Evans, K.V., Fanning, C.M., Mazdab, F.K., et al. (2012) Constraints on the Timing of Co-Cu Au Mineralization in the Blackbird District, Idaho, Using SHRIMP U-Pb Ages of Monazite and Xenotime Plus Zircon Ages of Related Mesoproterozoic Orthogneisses and Metasedimentary Rocks. Economic Geology, 107, 1143-1175. http://dx.doi.org/10.2113/econgeo.107.6.1143
- Baltybaev, S.K., Levchenkov, O.A., Glebovitskii, V.A., Rizvanova, N.G., Yakubovich, O.V. and Fedoseenko, A.M. (2010) Timing of the Regional Postmigmatitic K-Feldspar Mineralization on the Base of U-Pb Dating of Monazite (Metamorphic Complex of the Northern Ladoga Region). Doklady Earth Sciences, 430, 186-189. http://dx.doi.org/10.1134/S1028334X1002008X
- Bose, S., Dunkley, D.J., Dasgupta, S., Das, K. and Arima, M. (2011) India-Antarctica-Australia-Laurentia Connection in the Paleoproterozoic-Mesoproterozoic Revisited: Evidence from New Zircon U-Pb and Monazite Chemical Age Data from the Eastern Ghats Belt, India. Bulletin of the Geological Society of America, 123, 2031-2049. http://dx.doi.org/10.1130/B30336.1
- Dunning, G.R., Macdonald, A.S. and Barr, S.M. (1995) Zircon and Monazite U-Pb Dating of the Doi Inthanon Core Complex, Northern Thailand: Implications for Extension within the Indosinian Orogen. Tectonophysics, 251, 197. http://dx.doi.org/10.1016/0040-1951(95)00037-2
- Evans, J. and Zalasiewicz, J. (1996) U-Pb, Pb-Pb and Sm-Nd Dating of Authigenic Monazite: Implications for the Dia- genetic Evolution of the Welsh Basin. Earth and Planetary Science Letters, 144, 421. http://dx.doi.org/10.1016/S0012-821X(96)00177-X
- Peterman, E.M., Mattinson, J.M. and Hacker, B.R. (2012) Multi-Step TIMS and CA-TIMS Monazite U-Pb Geochrono- logy. Chemical Geology, 312-313, 58-73. http://dx.doi.org/10.1016/j.chemgeo.2012.04.006
- Rasmussen, B., Fletcher, I.R. and McNaughton, N.J. (2001) Dating Low-Grade Metamorphic Events by SHRIMP U-Pb Analysis of Monazite in Shales. Geology, 29, 963-966. http://dx.doi.org/10.1130/0091-7613(2001)029<0963:DLGMEB>2.0.CO;2
- Rasmussen, B., Fletcher, I.R., Muhling, J.R., Mueller, A.G. and Hall, G.C. (2007) Bushveld-Aged Fluid Flow, Peak Metamorphism, and Gold Mobilization in the Witwatersrand Basin, South Africa: Constraints from in Situ SHRIMP U-Pb Dating of Monazite and Xenotime. Geology, 35, 931-934. http://dx.doi.org/10.1130/G23588A.1
- Baumgartner, R., Romer, R.L., Moritz, R., Sallet, R. and Chiaradia, M. (2006) Columbite-Tantalite-Bearing Granitic Pegmatites from the Serido Belt, Northeastern Brazil: Genetic Constraints from U-Pb Dating and Pb Isotopes. Canadian Mineralogist, 44, 69-86. http://dx.doi.org/10.2113/gscanmin.44.1.69
- Camacho, A., Baadsgaard, H., Davis, D.W. and Cerny, P. (2012) Radiogenic Isotope Systematics of the Tanco and Sil- verleaf Granitic Pegmatites, Winnipeg River Pegmatite District, Manitoba. Canadian Mineralogist, 50, 1775-1792. http://dx.doi.org/10.3749/canmin.50.6.1775
- Melcher, F., Graupner, T., Henjes-Kunst, F., Oberthur, T., Sitnikova, M., Gabler, E., et al. (2008) Analytical Fingerprint of Columbite-Tantalite (Coltan) Mineralisation in Pegmatites―Focus on Africa. 9th International Congress for Applied Mineralogy, ICAM 2008, 8-10 September 2008, Brisbane, 615-624.
- Melleton, J., Gloaguen, E., Frei, D., Novak, M. and Breiter, K. (2012) How Are the Emplacement of Rare-Element Pegmatites, Regional Metamorphism and Magmatism Interrelated in the Moldanubian Domain of the Variscan Bohemian Massif, Czech Republic? Canadian Mineralogist, 50, 1751-1773. http://dx.doi.org/10.3749/canmin.50.6.1751
- Schmitt, A.K. and Zack, T. (2012) High-Sensitivity U-Pb Rutile Dating by Secondary Ion Mass Spectrometry (SIMS) with an O2+ Primary Beam. Chemical Geology, 332-333, 65-73. http://dx.doi.org/10.1016/j.chemgeo.2012.09.023
- Essex, R.M. and Gromet, L.P. (2000) U-Pb Dating of Prograde and Retrograde Titanite Growth during the Scandian O- rogeny. Geology, 28, 419-422. http://dx.doi.org/10.1130/0091-7613(2000)28<419:UDOPAR>2.0.CO;2
- Nesterova, N.S., Kirnozova, T.I. and Fugzan, M.M. (2011) New U-Pb Titanite Age Data on the Rocks from the Karelian Craton and the Belomorian Mobile Belt, Fennoscandian Shield. Geochemistry International, 49, 1161-1167. http://dx.doi.org/10.1134/S0016702911120081
- Spencer, K.J., Hacker, B.R., Kylander-Clark, A.R.C., Andersen, T.B., Cottle, J.M., Stearns, M.A., et al. (2013) Campaign-Style Titanite U-Pb Dating by Laser-Ablation ICP: Implications for Crustal Flow, Phase Transformations and Titanite Closure. Chemical Geology, 341, 84-101. http://dx.doi.org/10.1016/j.chemgeo.2012.11.012
- Richards, J.P., Cumming, G.L., Krstic, D., Wagner, P.A. and Spooner, E.T.C. (1988) Pb Isotope Constraints on the Age of Sulfide Ore Deposition and U-Pb Age of Late Uraninite Veining at the Musoshi Stratiform Copper Deposit, Central African Copper Belt, Zaire. Economic Geology, 83, 724-741. http://dx.doi.org/10.2113/gsecongeo.83.4.724
- Votyakov, S.L., Ivanov, K.S., Khiller, V.V., Bochkarev, V.S. and Erokhin, Y.V. (2011) Chemical Microprobe Th-U- Pb Age Dating of Monazite and Uraninite Grains from Granites of the Yamal Crystalline Basement. Doklady Earth Sciences, 439, 994-997. http://dx.doi.org/10.1134/S1028334X1107018X
- Li, X.-H., Li, W.-X., Wang, S.-C., Li, Q.-L., Liu, Y. and Tang, G.-J. (2009) Role of Mantle-Derived Magma in Genesis of Early Yanshanian Granites in the Nanling Range, South China: In Situ Zircon Hf-O Isotopic Constraints. Scientia Sinica Terrae, 39, 872-887. http://dx.doi.org/10.1007/s11430-009-0117-9
- Zheng, J.P., Griffin, W.L., Ma, Q., O’Reilly, S.Y., Xiong, Q., Tang, H.Y., et al. (2012) Accretion and Reworking beneath the North China Craton. Lithos, 149, 61-78. http://dx.doi.org/10.1016/j.lithos.2012.04.025
- Compston, W., Williams, I.S. and Clement, S.W. (1982) U-Pb Ages within Single Zircons Using a Sensitive High Mass-Resolution Ion Microprobe. The 30th Annual Conference on Mass Spectrometry and Allied Topics, Abstracts, Honolulu, 15 February 1984, B525-B534.
- Compston, W., Williams, I.S. and Meyer, C. (1984) U-Pb Geochronology of Zircons from Lunar Breccia 73217 Using a Sensitive High Mass-Resolution Ion Microprobe. Journal of Geophysical Research, 89, 525-534. http://dx.doi.org/10.1029/JB089iS02p0B525
- Feng, R., Machado, N. and Ludden, J. (1993) Lead Geochronology of Zircon by Laser Probe-Inductively Coupled Plasma Mass Spectrometry (LP-ICPMS). Geochimica et Cosmochimica Acta, 57, 3479-3486. http://dx.doi.org/10.1016/0016-7037(93)90553-9
- Srinivasan, G., Whitehouse, M.J., Weber, I. and Yamaguchi, A. (2004) U-Pb and Hf-W Chronometry of Zircons from Eucrite A881467. The 35th Lunar and Planetary Science Conference, League City, TX, 19 March 2004, 1709.
- Fong, C.F.C.M., Kee, D.D. and Kaloni, P.N. (2002) Advanced Mathematics for Engineering and Science. World Scientific Publishing Co. Pte. Ltd, Singapore.
- Wang, J., Qian, Z., Qian, W., Zhuang, Y., He, Y. and Pan, C. (1999) Analysis of Regression and Variance, in Probability Statistics (Engineering Mathematics). Tongji University, Shanghai, 240-247. (In Chinese)
- Bühlmann, P. and Mächler, M. (2008) Computational Statistics, 4-10. https://stat.ethz.ch/education/semesters/ss2012/CompStat/sk.pdf
Appendix A: Standard Error (1σ) for the Slope Using the Least Squares Method
The least squares method is described in textbooks on probability statistics [51] [52]. For a measured set of values (x1, y1,) … (xn,yn), there is a line:

that best fits the data. The quality of this line is determined by

When 
To find the minimum value for

giving

where 


The variance of a new predicted 

where σ is the standard error of 

if n is very small. Because k follows a Gaussian distribution, its variance is

The square root of this equation is the 1σ error of k.