Received 18 April 2016; accepted 26 June 2016; published 29 June 2016

ABSTRACT

We investigate a q-fractional integral equation with supremum and prove an existence theorem for it. We will prove that our q-integral equation has a solution in 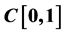which is monotonic on. The monotonicity measures of noncompactness due to Banaś and Olszowy and Darbo’s theorem are the main tools used in the proof of our main result.

Keywords:

q-Fractional, Integral Equation, Monotonic Solutions, Darbo Theorem, Monotonicity Measure of Noncompactness

1. Introduction

Jackson in [1] introduced the concept of quantum calculus (q-calculus). This area of research has rich history and several applications, see [2] - [4] and references therein. There are several developments and applications of the q-calculus in mathematical physics, especially concerning quantum mechanics, the theory of relativity and special functions [5] [4] . Recently, several researchers attracted their attention by the concept of q-calculus, and we could find several new results in [6] [7] and the references therein.

In several papers among them [8] - [11] , integral equations with nonsigular kernels have been studied. In [12] - [14] Darwish et al. introduced and studied the quadratic Volterra equations with supremum. Also, Banaś et al. and Darwish [13] [15] - [17] studied quadratic integral equations of arbitrary orders with singular kernels. In [18] , Darwish generalized and extended Banaś et al. [15] results to the perturbed quadratic integral equations of arbitrary orders with singular kernels.

In this paper, we will study the q-perturbed quadratic integral equation with supremum

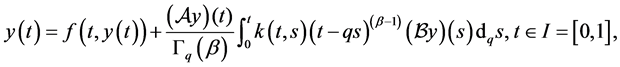(1)

where, , 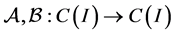and.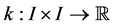

By using Darbo fixed point theorem and the monotonicity measure of noncompactness due to Banaś and Olszowy [19] , we prove the existence of monotonic solution to Equation (1) in.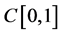

2. q-Calculus and Measure of Noncompactness

First, we collect basic definitions and results of the q-fractional integrals and q-derivatives, for more details, see [5] [6] [20] [21] and references therein.

First, for a real parameter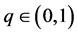, we define a q-real number 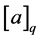by

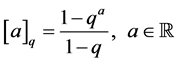, (2)

and a q-analog of the Pochhammer symbol (q-shifted factorial) is defined by

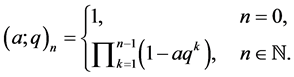(3)

Also, the q-analog of the power 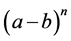is given by

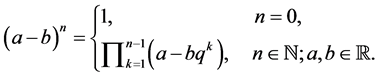(4)

Moreover,

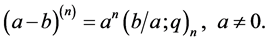(5)

Notice that, exists and we will denote it by.

More generally, for we define

(6)

and

(7)

Notice that. Therefore, if, then.

The q-gamma function is defined by

(8)

where Or, equivalently, and satisfies

Next, the q-derivative of a function f is given by

(9)

and the q-derivative of higher order of a function f is defined by

(10)

The q-integral of a function f defined on the interval is defined by

(11)

If f is given on the interval and then

(12)

The operator is defined by

(13)

The fundamental theorem of calculus satisfies for and, i.e., , and if f is continuous at, then.

The following four formulas will be used later in this paper

(14)

and

(15)

where denotes the q-derivative with respect to variable t.

Notice that, if and, then.

Definition 1. [2] Let f be a function defined on. The fractional q-integral of the Riemann-Liouville type of order is given by

(16)

Notice that, for, the above q-integral reduces to (11).

Definition 2. [2] The fractional q-derivative of the Riemann-Liouville type of order is given by

(17)

where denotes the smallest integer greater than or equal to.

In q-calculus, the derivative rule for the product of two functions and integration by parts formulas are

(18)

Lemma 1. Let and f be a function defined on. Then the following formulas are verified:

(19)

Lemma 2. [21] For, using q-integration by parts, we have

(20)

or

(21)

Second, we recall the basic concepts which we need throughout the paper about measure of noncompactness.

We assume that is a real Banach space with zero element and we denote by the closed ball with radius r and centered x, where.

Now, let and denote by and Conv X the closure and convex closure of X, respectively. Also, the symbols and stands for the usual algebraic operators on sets.

Moreover, the families and are defined by and respectively.

Definition 3. [22] Let If the following conditions

1).

2)

3)

4) and

5) if is a sequence of closed subsets of with and

then hold. Then, the mapping is said to be a measure of noncompactness in E.

Here, is the kernel of the measure of noncompactness.

Our result will establish in C(I) the Banach space of all defined, continuous and real functions on with.

Next, we defined the measure of noncompactness related to monotonicity in, see [19] [22] .

We fix a bounded subset of. For and denotes the modulus of continuity of the function y given by

. (22)

Moreover, we let

(23)

and

(24)

Define

(25)

and

(26)

Notice that, all functions in Y are nondecreasing on I if and only if.

Now, we define the map on as

(27)

Clearly, μ verifies all conditions in Definition 3 and, therefore it is a measure of noncompactness in [19] .

Definition 4.Let Let be a continuous operator. Suppose that maps bounded sets onto bounded ones. If there exists a bounded with, then is said to be satisfies the Darbo condition with respect to a measure of noncompactness.

If, then is called a contraction operator with respect to.

Theorem 1. [23] Let be a bounded, convex and closed subset of E. If is a Contraction operator with respect to. Then has at least one fixed point belongs to Q.

3. Existence Theorem

Let us consider the following suggestions:

a₁) is continuous and

Moreover, and

a₂) The superposition operator F generated by the function f satisfies for any nonnegative function y the condition, where c is the same constant as in a₁).

a₃) is a continuous operator which satisfies the Darbo condition for the measure of noncompactness with a constant. Also, if.

a₄).

a₅) The function is continuous on and nondecreasing and separately. Moreo-

ver,

a₆) is a continuous operator and there is a nondecreasing function such that for any. Moreover, for every function which is nonnegative on I, the function is nonnegative and nondecreasing on I.

a₇) such that

(28)

and.

Before, we state and prove our main theorem, we define the two operators and on as follows

(29)

and

(30)

respectively. Finding a fixed point of the operator defined on the space is equivalent to solving Equation (1).

Theorem 2. Assume the suggestions (a₁)-(a₇) be verified, then Equation (1) has at least one solution which is nondecreasing on I.

Proof. We divide the proof into seven steps for better readability.

Step 1: We will show that the operator maps into itself.

For this, it is sufficient to show that if. Fix and let and with. We have

(31)

Notice that, we have used

(32)

Notice that, since the function k is uniformly continuous on, then when we have that.

Thus, and therefore,

Step 2: applies into itself.

Now, , we have

(33)

Hence

(34)

Therefore, if we get from assumption a₇) the following

(35)

Therefore, maps into itself.

We define the subset of by

(36)

It is clear that is closed, convex and bounded.

Step 3: applies the set into itself.

By this facts and suggestions a₁), a₄) and a₆), we obtain transforms into itself.

Step 4: The operator is continuous on.

To prove this, we fix to be a sequence in with. We will show that.

Thus, we have,

(37)

Consequently,

(38)

As and are continuous operators, such that

(39)

Also, such that

(40)

Furthermore, such that

(41)

Now, take, then (38) gives us that

. (42)

This shows that is continuous in.

Step 5: In recognition of with respect to the quantity.

Now, we take Let us fix an arbitrarily number and choose and with. We will be supposed that because no generality will be loss. Then, by using our suggestions and inequality (31), we get

(43)

The last estimate implies

(44)

and, consequently,

(45)

Since the function k is uniformly continuous on and the function f is continuous on, then the last inequality gives us that

(46)

Step 6: In recognition of with respect to the quantity d.

Here, we fix an arbitrary and with. Then, by our assumption, we obtain our suggestions, we have

(47)

Now, we will prove that

(48)

We find that

(49)

But, because is increasing with respect to t, then

(50)

and, since is negative for then

(51)

Inequalities (50) and (51) imply that

This inequality and (47) gives us

(52)

The above estimate implies that

(53)

Therefore,

(54)

Step 7: is contraction with respect to the measure of noncompactness.

Inequalities (46) and (54) give us that

(55)

or

(56)

But, then

(57)

Inequality (57) enables us to use Theorem 1, then there are solutions to Equation (1) in.

This finishes our proof.

Cite this paper

Maryam Al-Yami, (2016) On Existence of Solutions of q-Perturbed Quadratic Integral Equations. American Journal of Computational Mathematics,06,166-176. doi: 10.4236/ajcm.2016.62018

References