American Journal of Molecular Biology
Vol.2 No.3(2012), Article ID:20995,5 pages DOI:10.4236/ajmb.2012.23030
Applying surface-based DNA computing for solving the dominating set problem
![]()
1Department of pathology, Tabriz University of Medical Sciences, Tabriz, Iran
2Department of Theoretical Physics and Astrophysics, Tabriz University, Tabriz, Iran
Email: *taghipourh@yahoo.com
Received 19 May 2012; revised 4 June 2012; accepted 25 June 2012
Keywords: Parallel Computing; Surface-Based DNA Computers; Dominating Set Problem; NP-Complete Problem
ABSTRACT
The surface-based DNA computing is one of the methods of DNA computing which uses DNA strands immobilized on a solid surface. In this paper, we applied surface-based DNA computing for solving the dominating set problem. At first step, surface-based DNA solution space was constructed by using appropriate DNA strands. Then, by application of a DNA parallel algorithm, dominating set problem was resolved in polynomial time.
1. INTRODUCTION
DNA molecules are genetic materials of organisms which are located in the cell nucleus. The unique and specific structure of DNA makes it one of the favorite candidates for computing purposes. In comparison with traditional electronics-based computers, DNA computers have massively parallel nature. While, a single DNA molecule can only carry out computation slowly, DNA computers can perform a very large and staggering number of calculations simultaneously. A DNA computer can perform 10^9 calculations per mL of DNA per second.
DNA computing was initially developed by Leonard Adleman in 1994 [1]. Adleman succeeded in solving seven-point Hamiltonian path problem solely by manipulating DNA molecules and suggested that DNA could be used to solve complex mathematical problems.
Surface-based DNA computing was introduced by Liu et al. in 1996 [2]. This model uses DNA molecules attached to a solid surface, instead of DNA molecules floating in a solution. This method greatly reduces losses of DNA molecules during different steps of computation.
In this paper, we applied the surface-based model for solving the dominating set problem which is one of the NP-complete problems. Dominating set problem is widely used in network routing, city planning, designing and construction of health services in appropriate places.
The paper is organized as follows. Section 2 introduces the DNA structure and various DNA computing models and discuss about surface-based DNA computing and biological operations which are used in surfacebased model. Section 3 introduces a DNA based algorithm for solving the dominating set problem in surface-based model.
2. BASICS OF DNA COMPUTING
2.1. Structure of DNA and DNA Computing Models
DNA consists of two long polymers of simple units called nucleotides. Nucleotides are building blocks of DNA and each of them contains three components: sugar, phosphate group and nitrogenous base. There are four different nitrogenous bases which contribute in DNA structure: Thymine(T) and Cytosine(C) which are called pyrimidines; Adenine(A) and Guanine(G) which are called purines. The nucleotides are link together by phosphordiester bonds and form single stranded DNA (ssDNA). Two ssDNA molecules join together to form double stranded DNA (DsDNA) based on complementary rule: “A” always pairs with “T”, and likewise “C” pairs with “G”. In Figure 1, a schematic picture of nucleotide is shown.
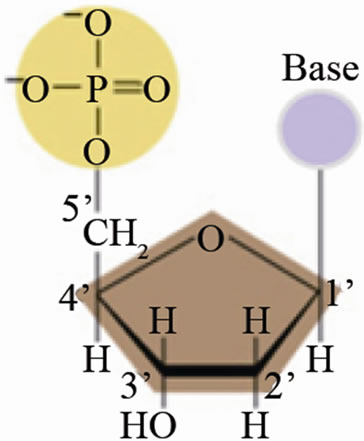
Figure 1. A nucleotide.
DNA computing was initially developed by Leonard Adleman in 1994 [1]. Adleman resolved an instance of Hamiltonian path problem just by handling the DNA molecules. In 1995, Lipton [3] presented a method for solving the satisfiability (SAT) problem. Adleman-Lipton model can be used to solve different NP-complete problems. In Adleman-Lipton model, DNA splints are used for construction of solution space. Adleman [4,5] also presented a molecular algorithm for solving the 3-coloring problem. Chang and Guo [6-8] showed that the DNA operations in Adelman-Lipton model could be used for developing DNA algorithms to resolve the dominating set problem, the vertex cover problem, the maximal clique problem and independent set problem.
The surface-based model was introduced by Liu et al. in 1996 [2]. This model uses DNA molecules attached to a solid surface, instead of DNA molecules floating in a solution. Liu et al. also proposed a surface-based DNA algorithm for solving the satisfiability problem.
In 1996, Roweis et al. [9] introduced the Sticker based DNA computing model and applied it in solving the Minimal Set Cover problem. Perez-Jimenez and Sanchocaparrini [10] used Sticker based DNA computing to resolve knapsack problem, and this model also were applied for breaking the Data Encryption Standard (DES) [11,12]. In our previous work, we also applied sticker model for solving the independent set problem [13].
Other than Adleman-Lipton, surface-based and Sticker based models, other various models are also proposed in DNA computing by researchers. Quyang et al. [14] solved the maximal clique problem using DNA molecules and Restriction endonuclease enzymes. Amos et al. [15,16] described a DNA computation model using restriction endonuclease enzymes instead of successive cycles of separation by DNA hybridization, which can reduce the error-rate of computation. Hagiya et al. [17] proposed a new method of DNA computing that involves a selfacting DNA molecule containing both the input, program, and working memory. In this method, a single-stranded DNA molecule consists of an input segment on the 5’-end, followed by a formula (program) segment, followed by a spacer, and finally with a “head” on the 3’-end that moves and performs the computation. Another method for DNA computation is “computation by self-assembly”. Eric winfree et al. [18-20] introduced a linear and 2-dimentional self-assembly model.
The computing by blocking was introduced by Rozenberg et al. [21] This model uses a novel approach to filter the DNA molecules: Instead of separating the DNA strands to distinct tubes, or destroy and removing the DNA molecules that does not contribute to finding a solution, it blocks (inactivates) them in a way that the blocked strands can be considered as non-existent during the subsequent steps of computation.
2.2. Surface-Based DNA Computation
2.2.1. General Aspects of Surface-Based Model
The surface-based model was introduced by Liu et al. in 1996 [2]. This model uses DNA molecules attached to a solid surface, instead of DNA molecules floating in a solution. The solution set of DNA strands is initially attached to a surface (glass, silicon, gold, for example). The immobilized DNA strands are then subjected to biological operations such as hybridization or exonuclease degradation, in order to extract the desired DNA strands. This model greatly reduces losses of DNA molecules during different steps of computation. Briefly, the basic operations in surface-based model are as follows: selectively mark strands, destroy either marked or unmarked strands, and unmark all marked strands. Another feature of surface-based model is the use of single-base mismatch discrimination in hybridization as a basis for selectively marking DNA strands, which allows obtaining a high density of information per nucleotide.
2.2.2. Biological Operations in Surface-Based Model
For simplicity, let’s consider that the solution space be the set S of binary strands of length n. The following operations may be performed on S [2].
1) mark (i, b): this marks all strings in which the ith bit has value b. This operation is performed by annealing specific probes to desired DNA strands.
2) mark ((i1, b1), (i2, b2), ··, (ik, bk)): this is an extension of mark (i, b) which marks a desired string based on the values of multiple bits. This operation is also performed by annealing specific probes to desired DNA strands.
3) destroy-marked: removes all marked strands (double stranded DNA molecules) from solution space. This is performed by specific enzymes which selectively destroy double stranded DNA molecules.
4) destroy-unmarked: removes all unmarked strands (single stranded DNA molecules) from solution space. This is performed by specific enzymes which selectively destroy single stranded DNA molecules.
5) unmark: this unmarks all marked strands in solution space (dissociate probes from immobilized DNA strands and converts double stranded molecules to single stranded DNA molecules).
6) test-if-empty: this operation determines whether the set S is empty or not. It is usually executed at the end of computation.
2.2.3. Designing of Appropriate DNA Strands and Construction of Solution Space
First of all, it is essential to represent all possible binary strings of length n as DNA strands. In order to synthesis DNA strands attached to solid surface, a desired DNA molecule is synthesized nucleotide by nucleotide on a support particle in sequential coupling steps. By application of this method, we can produce combinatorial sets of molecules by using mixture of nucleotides at each coupling step. For example, if two nucleotides are used together in four coupling steps, 16 different DNA strands will be produced on solid support.
In this article, we use one base to represent one bit of the binary strings, while keeping the GC content of the string constant (about 50%). For example, we can use A or T in half of the positions to represent 0 and 1 respectively, and G or C in the remaining positions to represent 0 and 1 respectively. This is an important rule in designing of DNA strands, because GC content has a very strong effect on DNA hybridization reactions. In addition, all DNA strands immobilized on solid surface have markers at each end; these will be used as binding sites for primers of PCR reaction. The length of binding sites of primers is about 20 nucleotides. PCR reactions will be used for amplifying the desired DNA molecules.
2.2.4. In Vitro Implementation of Operations
We now describe how each of the operations of surfacebased model can be performed on surfaces.
mark (i, b): in order to marking the DNA strands which represent binary strings in which the ith bit is b, first, the DNA probes that are complementary to the mentioned strands are synthesized. Then, each of these probes hybridizes to its complement DNA strand on the surface. Thus, the marked DNA strands will be doublestranded whereas unmarked strands remain singlestranded.
In this method, single-base mismatch is used for discrimination of marked and unmarked strands, and it was determined that excellent discrimination based on singlebase mismatch is obtained using 15 mer sequences.
destroy-marked, destroy-unmarked: Either marked (double-stranded) or unmarked (single-stranded) DNA molecules may be selectively destroyed by using exonuclease enzymes.
unmark: This operation is performed simply by washing the surface in distilled water. Distilled water is low tonic solution which denature double-stranded DNA molecules and leads probes to dissociate from immobilized DNA strings and are washed away, leaving only the original single-stranded DNA attached to the surface.
test-if-empty: As mentioned before, this operation is usually executed at the end of computation. In final step, the remaining DNA molecules may be marked (doublestranded) or unmarked (single-stranded). If remaining DNA molecules are unmarked (single-stranded), we can cleave them from the surface, and amplify them by using PCR and detect if there is any product as a result. But, if the remaining DNA molecules on the surface are marked (double-stranded), we should convert them to unmarked strands by removing complementary probes from immobilized DNA strands, and then, cleave them from the surface, amplify by using PCR and detect if there is any product as result.
3. SOLVING THE DOMINATING SET PROBLEM BY SURFACE-BASED DNA COMPUTERS
3.1. Definition of the Dominating Set Problem
In graph theory, a dominating set of a graph G = (V, E), where V is the set of the vertices and E is the set of the edges, is a subset V1 Í V such that for all u Î V − V1 there is a v Î V1 for which (u, v) Î E. The size of a dominating set is the number of vertices it contains. The dominating set problem is to find a minimum size dominating set in G. The dominating set problem has been proved to be a NP—complete problem. For example, the graph in Figure 2 includes 7 vertices and 6 edges.
It is clear that the minimum size dominating set for our graph is {V4, V5}, furthermore, the size of the dominating set problem in our graph is 2.
3.2. Construction of the Surface-Based Solution Space for Dominating Set Problem
First of all, it is essential to generate the surface-based DNA solution space of our problem. Then, basic biological operations will be used to select legal strands and remove illegal strands from the solution space. It is obvious that a graph with N vertices has 2N subset of vertices or 2N possible dominating sets. Furthermore, each possible dominating set can be represented by an N-digit binary number. Also suppose that V1 is a dominating set of G. If the ith bit in an N-digit binary number is set to 1, it represents that the ith vertex is in V1 but is not in V-V1. If the ith bit in an N-digit binary number is set to 0, it represents that the ith vertex is not in V1 but is found in V − V1.
Our graph has 7 vertices and 128 possible dominating sets. Furthermore, the solution space has 128 distinct molecules, which have designed and synthesized as
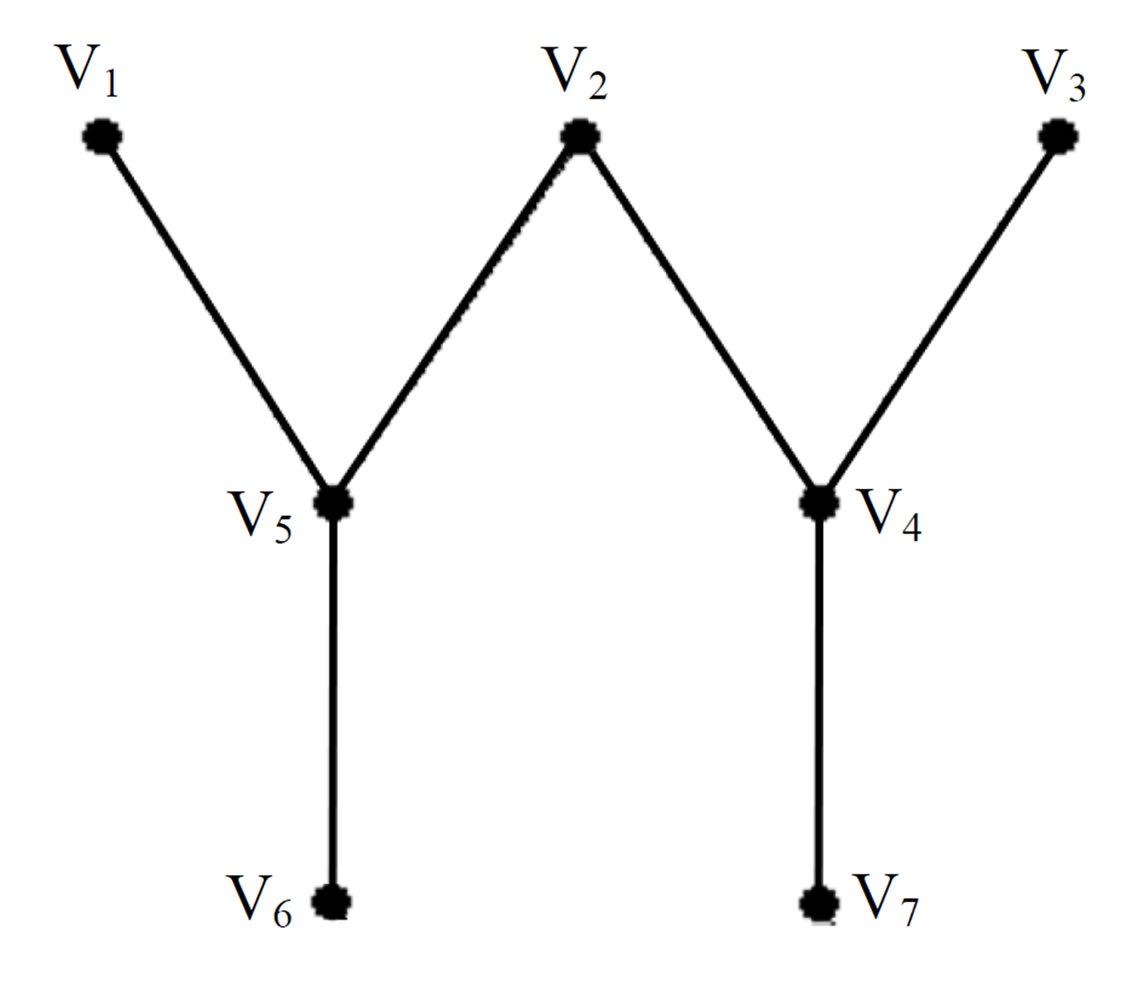
Figure 2. The graph of our problem.
shown in Figure 3. The length of these DNA molecules is 55 nucleotides, consisting of a unique 20 nucleotides sequence at each end (binding sites for PCR primers), and a 15 nucleotides hybridization sequence in the middle. As discussed before, excellent specificity and discrimination based on single-base mismatch is obtained using 15 mer sequences, for this reason, we considered 15 nucleotides for hybridization sequence. The graph of our problem have 7 vertices, thus, the 7 central nucleotides in the 15 mer hybridization sequence were synthesized as a combinatorial set with two possibilities at each position: (G + C) (G + C) (G + C) (G + C) (A + T) (A + T) (A + T), representing 27 = 128 distinct molecules in solution space. The adjacent 4 nucleotides at the two ends of the hybridization sequence have unique and constant sequences in order to limit the size of the solution space to 128 molecules.
3.3. DNA Algorithm for Solving the Dominating Set Problem
The following algorithm is proposed for solving the dominating set problem:
1) Prepare solution space by designing and synthesis of appropriate DNA strands which are immobilized on a surface.
2) For i = 1 to n, where n is the number of vertices in the graph G.
a) mark (i, 1);
b) For each vertex Vj which have adjacency to Vi;
c) mark (j, 1);
d) destroy-unmarked;
e) unmark.
3) Cleave remaining immobilized DNA strings from surface.
4) Amplify by PCR.
5) Input DNA molecules to tube T0.
6) For i = 0 to n – 1 For j = i down to 0 Separate (Tj, i + 1) → (T(j+1)’, Tj)
Combine (Tj+1, Tj+1, T(j+1)’)
7) Read T1; else if it was empty then:
Read T2; else if it was empty then:
Read T3; else if it was empty then:
.
.
.
Read Tn–1; else if it was empty then:
Read Tn.
According to the steps in the algorithm, the dominating set problem can be resolved by surface-based DNA computation in polynomial time.
Step 2 of the algorithm is executed n times (n is 7 in our graph). Step 2a, marks the DNA strands which contain the vertex Vi and the DNA strands which do not contain the vertex Vi remain unmark. From the definition of dominating set, the unmarked DNA strands represent sets V − V1, which do not contain the vertex Vi. If there is no vertex adjacent to Vi, then step 2d will destroy the unmarked DNA strands. Otherwise, step 2c will be executed z times, where z is the number of vertices adjacent (directly connected by an edge) to Vi. Each time step 2c is executed, it marks DNA strands which contain Vj (subsets which contain vertices that have adjacency to Vi). Furthermore, the remaining unmarked DNA strands consist of all of the strands which do not contain Vi and Vj, or we can say it contains vertices which do not have adjacency to Vi. Thus, the unmarked DNA strands are illegal strands and should be destroyed. For all vertices, similar processing is also performed, therefore, at the end of step 2, illegal strands will be destroyed and only legal strands (representing dominating sets) will be remain in solution space.
During steps 3 to 5, legal DNA strands which remain on surface at the end of step 2, are cleaved from surface, amplified by using PCR, and finally, all of them are transferred to tube T0.
In step 6 of the algorithm, we applied 2 operations: separation and combination. Here, we briefly discuss about these operations:
Separate (Ta, i) ® (Tb, Tc), this operation creates two new tubes Tb and TcTb contains the DNA molecules having the ith bit value 1 (Tb = +(Ta, i)) and Tc contains the DNA molecules having the ith bit value 0 (Tc = –(Ta, i)).
Combine (Ta, Tb, Tc): the DNA molecules from the tubes Tb and Tc are combined to form a new tube Ta, simply the contents of Tb and Tc are poured to tube Ta. (Ta= Tb ∪ Tc).
By the execution of step 6, the DNA strands which represent the Æ subset are placed in tube T0, the DNA strands represent the subsets which contain only one vertex are placed in tube T1, the DNA strands represent the subsets which contain two vertices are placed in tube T2, the DNA strands represent the subsets which contain 3 vertices are placed in tube T3, and so on.
In step 7, all of the tubes (from T1 to Tn) are evaluated for presence of DNA strands , and the first tube which is not empty and contains DNA strands represent minimum

Figure 3. Representation of the solution space for our problem.
size dominating set. In our example, tube T1 is empty and devoid of any DNA strands. The first tube which contains DNA molecules is tube T2 which represent the subset {V4, V5}. Hence, the minimum size dominating set in our graph is 2.
4. CONCLUSIONS
In this paper, the surface-based DNA computing was used for solving the dominating set problem. This method could be used for solving other NP-complete problems.
The loss of DNA molecules is one of the major problems in Adleman-Lipton and sticker models, but the surface-based model greatly reduces losses of DNA molecules during different steps of computation. One of the major limitations of this model is that the length of hybridization sequence is restricted to 15 nucleotides, because selectively marking DNA strands is based on single-base mismatch discrimination in hybridization. For solving the large scale NP-complete problems, it is essential to design the oligos larger than 15 nucleotides.
Finally, for improving the efficiency and capabilities of surface-based model, other operations should be added to this model.
REFERENCES
- Adleman, L.M. (1994) Molecular computation of solutions to combinatorial problems. Science, 266, 1021-1024. doi:10.1126/science.7973651
- Liu, Q., et al. (1996) A surface-based approach to DNA computation. Proceedings of the 2nd Annual Meeting on DNA Based Computers.
- Lipton, R.J. (1995) DNA solution of hard computational problems. Science, 268, 542-545. doi:10.1126/science.7725098
- Adleman, L.M. (1995) On constructing a molecular computer. Manuscript. University of Southern California.
- Adleman, L.M. (1996) On constructing a molecular computer. DNA Based Computers, 1-22.
- Chang,W.-L. and Guo, M. (2002) Solving the dominating-set problem in Adleman-Lipton’s model. The Third International Conference on Parallel and Distributed Computing, Applications and Technologies, Kanazawa, 4-6 September 2002, 167-172.
- Chang, W.-L. and Guo, M. (2002) Solving the clique problem and the vertex cover problem in Adleman-Lipton’s model. IASTED International Conference on Networks, Parallel and Distributed Processing, and Applications, Tsukuba, 2-4 October 2002, 431-436.
- Chang, W.-L. and Guo, M. (2002) Solving NP-complete problem in the Adleman-Lipton model. The Proceedings of 2002 International Conference on Computer and Information Technology, 11-13 September 2002, 157-162.
- Roweis, S., et al. (1999) A sticker based model for DNA computation. In: Landweber, L., Baum, E., Eds., Second Annual Workshop on DNA Computing, Princeton University, 1-29.
- Perez-Jimenez, M.J., Sancho-Caparrini, F. (2001) Solving knapsack problems in a sticker based model. Lecture Notes in Computer Science, 2340, 161-171.
- Adleman, L., Rothemund, p., Roweis, S. and Winfree, E. (1999) On applying molecular computation to the data encryption standard. The 2nd Annual Workshop on DNA Computing, Princeton University, 31-44.
- Boneh, D., Dunworth, C. and Lipton, R. (1996) Breaking DES using a molecular computer.
- Taghipour, H., Taghipour, A., Rezaei, M. and Esmaili, H. (2012) Solving the independent set problem by sticker based DNA computers. American Journal of Molecular Biology, 2, 153-158. doi:10.4236/ajmb.2012.22017
- Quyang, Q., Kaplan, P.D., Liu, S. and Libchaber, A. (1997) DNA solution of the maximal clique problem. Science, 278, 446-449. doi:10.1126/science.278.5337.446
- Amos, M., Gibbons, A. and Hodgson, D. (1996) Errorresistant implementation of DNA computations. Proceedings of the 2nd DIMACS Workshop on DNA Based Computers, 87-101.
- Amos, M., Gibbons, A. and Hodgson, D. (1996) A new model of DNA computation. 12th British Colloquium on Theoretical Computer Science, 1-4.
- Hagiya, M., Arita, M., Kiga, D., Sakamoto, K. and Yokoyama, S. (1999) Towards parallel evaluation and learning of boolean μ-formulas with molecules. DIMACS Series in Discrete Mathematics and Theoretical Computer Science, 48, 57-72.
- Winfree, E. (1998) Simulations of computing by selfassembly. Fourth International Meeting on DNA Based Computers, 213-239.
- Winfree, E., Liu, F.L., Wenzler, L.A. and Seeman, N.C. (1998) Design and self-assembly of two-dimensional DNA crystals. Nature, 394, 539-544. doi:10.1038/28998
- Winfree, E., Yang, X. and Seeman, N.C. (1996) Universal computation via self-assembly of DNA: Some theory and experiments. Proceedings of the 2nd DIMACS Workshop on DNA Based Computers.
- Rozenberg, G. and Spaink, H. (2003) DNA computing by blocking. Theoretical Computer Science, 292, 653-665. doi:10.1016/S0304-3975(01)00194-3
NOTES
*Corresponding author.

