American Journal of Operations Research
Vol.06 No.01(2016), Article ID:63252,14 pages
10.4236/ajor.2016.61012
A Novel Statistical Analysis for Residual Stress in Injection Molding
Faisal Alkaabneh, Mahmoud Barghash, Yousef Abdullat
University of Jordan, Amman, Jordan

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 November 2015; accepted 24 January 2016; published 29 January 2016
ABSTRACT
Residual stresses can reduce the reliability of plastic injection molding parts. This work is an attempt to model the residual stresses as a function of injection molding parameters. More stress is placed on reducing the number of input factors and to include all possible interactions. For this purpose, two-stage experimentation is suggested: a factor screening stage and Response Surface optimization stage. In screening stage Taguchi 3 level experimental design is used to classify the input parameters as significant and non-significant factors. Eight input variables were classified into 3 non-significant and 5 significant factors using this screening stage. Thus for the Response Surface optimization stage: instead of doing 160 experiments in Central Composite, 56 are only needed after the screening stage in half Central Composite Design. The best subset and regression model fitting tools in addition to model verification using randomly selected input setting were used to select a model for predicting residual stresses with a verified Root Mean Square Error (RSME) of nearly 0.93 MPa.
Keywords:
Injection Molding, Multi-Stage Experimental Design, Taguchi Experimental Design, Response Surface Methodology, Regression Analysis

1. Introduction
The plastic injection molding process is a widely used polymer processing operation [1] . Because injection molding has many advantages, such as short production cycles, excellent surfaces of the products, and facile molding of complicated shapes, so it is the most popular molding process for making thermoplastic parts [2] . The plastic injection molding process is a cyclic process which consists of three stages. These stages are filling and packing stage, cooling stage and ejection stage [3] . Plastic injection molding is one of the most important methods applied for forming thin-shell plastic products in industry [4] . This is especially suitable for the house hold electronic equipment manufacturing processes. The application of computer, communication and consumer electronics (3C) products such as portable computer and cell phone, etc. was widely used in the whole world. The vigorous development of 3C products has had the trend for products to be light, thin, short and small [5] .
As the wall thickness of plastic parts becomes thinner, the injection molding operation becomes more difficult. Hence, the industry has the demand for techniques of plastic injection molding to produce plastic parts with thin wall features [6] [7] . For example, today cell phone dimensions are getting smaller and their appearances are getting more esthetic. Besides these properties, users care about phones’ durability. Users do not want that falling to the ground, taking impact, exposing to force cause damage to the cell phone. The part which is produced by using injection molding method does not have the desired strength and resistance to impact, because of the residual stress problem encountered those days in the industry. Residual stresses are internal stresses of the molded part in the absence of external forces. They are caused mainly by non-uniform temperature profile in the cavity during filling, packing, and cooling stages [8] . It is known that the residual stress is produced due to high pressure, temperature change, and relaxation of polymer chains, resulting in shrinkage and warpage of the part [9] . Internal stresses in injection molding components are a principal cause of shrinkage and warpage, and are considered to be responsible for environmental stress cracking in plastic parts [10] [11] . The best way to prevent high residual stress problem is to choose the plastic material and injection parameters right. The decrease in the thickness of the part also weakens the strength of the part; however, increasing thickness of plastic parts is not a feasible solution as the demand of the cell phone design requires parts to be thin, light and small. This problem can be solved by choosing the appropriate material for the durability. But a material may be appropriate for the strength may not be appropriate for the application of that part. Thus, one important solution is to minimize residual stresses by optimizing the process factors of the injection molding process.
Manufacturing process optimization is of three main parts, experimentation, modeling and searching. Experimentation may be actual running of the experimentation on the injection molding process or using Finite element software’s prior to finalizing the design. The modern computational and simulation tools for injection- molding process have matured to a stage where they can provide substantial insight into the process metrics and can be profitably utilized to help improve the design of injection-molded components [12] . Computer aided engineering (CAE) has made a major impact on the design and manufacturing process in the injection molding industry in terms of both quality improvement and cost reduction based on applications of various computer simulation techniques [13] . In the past, the optimization of the process parameters was considered to be a “black art”, which relied heavily on the experience and knowledge of experts and required a trial-and-error process [14] . Currently, Design of experiments (DOE) is grabbing much attention within the perspective of manufacturing process optimization. DOE has been a very useful tool to design and analyze complicated industrial design problems. It helps us to understand process characteristics and to investigate how inputs affect responses based on statistical backgrounds. In addition, it has been used to systematically determine the optimal process parameters with fewer testing trials [15] . A widely DOE methodology is Taguchi Experimental Design (DOE), which various industries have used over the years to improve products or manufacturing processes. It is a powerful and effective method to solve challenging quality problems [16] . Taguchi analysis is a useful methodology for optimizing process that does not include interaction factors. One main reason for using Taguchi experimentation is the low number of experiments which excludes interactions, and this scatters some shadows on the accuracy of the regression model built using this experimentation type. Thus, it can improve some processes but may not give the optimal. A more comprehensive approach is Response Surface which includes all interaction effects but requires heavy experimentation and data collection. The regression models that can be further used for optimization are more accurate in the Response Surface experimental design. But, Response Surface has extensive experimentation and cost which places some restrictions on the use of this important technique.
A recent published article [17] , where the authors developed, for the first time, a new framework to analyze and optimize different manufacturing process setting of plastic injection modeling to minimize different defects via a multi-objective multi-criteria process through using integrated Analytical Hierarchy Process (AHP) wish Taguchi DOE.
This work suggests an intermediate approach that uses both advantages of two main experimentation types whereby, Taguchi Experimental Design (TED) is used for significant factor determination and Response Surface is used for modeling the process residual stresses. This study introduces an innovative method to model the residual stresses based on injection molding process settings; namely filling time, melt temperature, mold temperature, switch to pack (%), pressure holding time, holding pressure magnitude, cooling time, and cooling inlet temperature. This method firstly, uses experiment runs based on Taguchi Orthogonal Array (OA) with only main effects of the input variables included. Secondly, the input parameters are classified using Analysis Of Variance (ANOVA) into significant and non-significant factors. Thirdly, Response Surface design of experiment is conducted using only significant factors identified in the previous step. Fourthly, regression models is developed based on data generated from the Response Surface design of experiment and then validation tests are conducted to choose the best regression model based on the minimum Root Mean Square Error (RSME).
This paper successfully applies multi-stage experimentation, namely, Taguchi and central composite design to model and optimize the residual stress. The residual stress is extremely important as it reduces the reliability of parts in case of tension or improves it in case of compression. The number of experiments and thus time to design and time to customer can be reduced appreciably by this technique.
2. Research Methods
2.1. Taguchi Method and Signal to Noise S/N Ratio
Taguchi methods have been used widely in engineering analysis to optimize the performance characteristics through the setting of design parameters. Taguchi method is also strong tool for the design of high quality systems. To optimize designs for quality, performance, and cost, Taguchi method presents a systematic approach that is simple and effective [18] . The Taguchi method consists of three stages which are system, parameters, and tolerance designs, respectively. The system design involves the application of scientific and engineering knowledge required in manufacturing of a product. The parameter design is employed to find optimal process values for improving of the quality characteristics.
The tolerance design is used for determining and analyzing of the tolerances in optimal settings recommended by the parameter design [19] . Taguchi recommends the use of the S/N ratio for determination of the quality characteristics implemented in engineering design problems. The S/N ratio characteristics with signed-target type can be divided into three stages: the smaller is the better, the nominal is the best, and the larger is the better [20] . The quality characteristics are evaluated through the S/N ratio obtained in the Taguchi experimental plan. ANOVA then can be used to evaluate the experimental errors and test of significance to understand the effect of various factors [21] .
2.2. Response Surface Methodology
Response surface methodology is an integration of mathematical and statistical techniques for modeling and optimizing the response variable models involving several quantitative independent variables. It is well adapted to making an analytical model for complicated problems. In industry, RSM is a very useful tool for quality and productivity improvement, in which often we wish to discover functional relationships between the response and independent variables. Upon determining the relationship, we can easily resolve practical quality and productivity problems by using appropriate statistical techniques [22] . In general, for predicting the optimal point, a second-order polynomial function was popularly used and fitted to correlate the relationship between independent variables (Xi) and response (Y). The quadratic response surface is always described as follows.
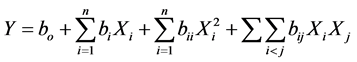 (1)
(1)
where n is the number of design variables, and bo, bi, bii, and bij represent the coefficients of constant, linear, quadratic, and cross product terms, respectively. To build the empirical response models, the necessary data are generally collected by the design of experiments, followed by the statistical single or multiple regression technique. The more popular statistical approach such as analysis of variance (ANOVA) is adopted to justify the significance of the empirical model [23] .
2.3. Regression Model Development
The purpose of multidimensional analysis of regression is to determine the quantitative relations between the investigated values and the variables, which directly influence them to assess the results of their activity and to predict the behavior of the investigated variables [24] . Regression analysis is also one of the most widely used statistical tools because it provides simple methods for establishing functional relationship among variables. It can be employed to develop a suitable model for predicting dependent variables from a set of independent variables [25] .
3. Methodology
Figure 1 shows the proposed scheme in our study. In phase 1 (planning) Taguchi experimental plan was first conducted using reduced number of experiments, time and cost based on orthogonal arrays to determine the most significant factors. In phase 2, a Response Surface Methodology (RSM) Central Composite design is conducted based on the identified significant factors in phase 1. In Phase 3 (modeling quality characteristic) data obtained from Response Surface experiments are used to develop 3 regression models then validation tests are conducted to choose the best model yielding minimum Root Mean Square Error (RSME).
4. Case Study
4.1. Part Geometry and Finite Element Model
Finite Element (FE) analysis of the cell phone cover part is performed using SimpoeMesh [26] . Geometry of the part employed in this current study having width, length, height and thickness of 83, 145, 17 and 2 mm respectively was shown in Figures 2(a)-(c). FE model of the part is created by discrediting the geometry into smaller simple elements. The FE model shown in Figure 2(d) includes 6884 tetrahedron elements having average aspect ratio of 3.2068. The FE analyses were performed using Simpoe-Mold software.
4.2. Mold and Material Description
The study analysis is conducted for ABS + PC (P) SABIC/Cycoloy CY6110 material; its properties are given in Table 1. Water is used as the cooling fluid, steel 420SS as mold material. The gate location is shown Figure 3(a) having 2 mm diameter. The cooling channels are shown in Figure 3(b) and cooling channels properties are given in Table 2.
4.3. Phase 1: Screening Stage Design and Analysis
4.3.1. Taguchi Screening Experiments Experimental Design
Taguchi Method was developed for saving time, cost and effort. Minitab 15 software was used for statistical calculations [27] . The factor levels for the eight included variables are given in Table 3. The levels for each factor are set based on literature, materials data sheets, and experience. Tests were organized using Taguchi’s L27 (3^8) orthogonal array (Table 4 columns 2 - 9). This orthogonal array is efficient for screening purpose. It can give the significance of the different input variables with minimum number of experiments. Table 4-column
Figure 1. The proposed methodology.



Figure 2. (a) and (b) CAD drawings of the part, (c) general view and (d) finite element model.
Table 1. Material properties of ABS + PC.

Figure 3. (a) Gate location, (b) cooling channels configuration.
Table 2. Selected cooling channel parameters.
Table 3. The process parameters and their levels.
10 shows the experimental results obtained from Simpoe-Mold [28] . The test results were evaluated in terms of S/N ratio (Table 4 column 11). The S/N ratio was calculated by smaller the better quality characteristic for determining the effect of each factor on the selected injection molding quality characteristic according to the equation [29] :
 (2)
(2)
where 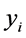 is the measured property and
is the measured property and 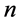 corresponds to the number of samples in each test trial.
corresponds to the number of samples in each test trial.
4.3.2. Screening Stage Factor Analysis
Figure 4 shows the factors plot curves using MINITAB. It is clear that factors A, D, E, F, and G are of the highest effect on the residual stresses and the other factors have slight effect within the specified range of the experimentation.
According to Figure 4 the optimal value for the residual stresses can be obtained using the combination of A
Table 4. The Taguchi L27 orthogonal array, experimental results, and S/N ratio.
Figure 4. Plot of process effects for residual stresses.
(Filling time) 1s, B (Melt temperature) 250˚C, C (Mold temperature) 60˚C, D (Switch to pack %) 50%, E (Pressure holding time) 6s, F (Cooling time) 12s, G (Holding pressure magnitude) 60 MPa, and H (Cooling inlet temperature) 20˚C, is 13.3111 MPa.
Table 5 shows the ANOVA significance analysis for the factors. Considering the 5% P-significance level, factors A, D, E, F, and G are considered significant and this result coincides perfectly with Figure 4.
Factors screening requires less experiments and is effective in this sense to identify if the input machine setting is significant enough to be included in further analysis. As, is seen in this work, half of input factors are not significant and should not be included in the model building experimental design part.
4.4. Response Surface Methodology
As discussed above the RSM is high costly and time consuming. The cost increases exponentially as the number of factors increase. Thus, in this work we have included a factor screening phase whereby, we exclude any non- significant factors prior to modeling.
In this study, the approximation of the mathematical model will be proposed using the fitted third-order polynomial regression model, which is called the cubic model. The necessary data for building the response model are generally collected by the experimental design [30] .
The significant factors regarding residual stresses for Response Surface experiments are screened from the injection process parameters through the Taguchi experiments based on P-value of 0.05 that is 95% confidence interval. Filling time, switch to pack percentage, pressure holding time, holding pressure magnitude, and cooling time are found to be the significant factors in these screening tests. In this study, the experimental design adopts the centered central composite design (CCD) in order to fit the cubic model of the RSM. The factorial portion of CCD is a full factorial design with all combinations of the factors at two levels and composed of the eight star (axial) points, and six central points in cubes (coded level 0) which is the midpoint between the high and low levels. The star points are at the face of the cube portion on the design which corresponds to an alpha (α) value of 2.366. This type of design is commonly called the face-centered CCD.
Table 6 shows the five process factors and their levels. The experimental plans is generated using stipulated conditions based on the face centered CCD and involves 56 total runs as shown in Table 7. Table 7 shows the experiments layout and results.
Table 5. ANOVA results.
Table 6. Process factors and their levels for the full factorial experimental design.
Table 7. Experiments layout and their results.
Phase 3: Regression Modeling and Model Selection of the Residual Stresses
The best subset tool is used in modeling the residual stresses. Table 8 shows the results for the best subset. Column 1 shows the number of variables included in the test, columns 2 and 3 are the non-adjusted and adjusted regression correlation factor, respectively, and column 4 is called the Mallows CP. In statistics, Mallows suggested for model selection, among input variables, and the goal is to find the best model involving a subset of these predictors. The lower, the CP factor the better the model is [31] .
Although many of the mentioned models are good in terms of the adjusted R square, the Mallows CP suggests that the best model is the twenty third model. And because of the close value of the CP for the last three models, they are included in further processing for the selection of the best model. These models for the recommended variables are fitted using Minitab and the fitness results are given in equations 3 - 5.



1) Verification results
Table 9 shows the verification results for some randomly selected experiments. Columns 2 through 6 show the selected values for the Filling time (A), Switch to pack % (B), Pressure holding time (C), Holding pressure magnitude (D), and Cooling time (E). The predictions for the Models 1 - 3 in Table 9 are shown in columns 7 - 9. The actual results are in column 10, while Table 10 shows the absolute errors associated with each model, row 7 shows the RSME for the three models. Form Table 10, the best model is model 3 with The RSME value of 0.930751.
Table 8. Best subset results for residual stress modeling.
2) Model graphical illustration and optimization
Figures 5(a)-(c) shows a 3D fitted Response Surface of the residual stresses for the significant variables.
Table 9. Random points verification of the suggested models.
Table 10. Error calculation for each suggested model.


Figure 5. 3D illustration plots for the residual stress versus other input variables. The optimal combination discussed above (Filling time, 1s; Switch to pack percentage, 80%; Pressure holding time, 11s; Cooling time, 16s; and Holding pressure magnitude, 35 MPa) was verified and it gave residual stresses of 7.0125 MPa.
According to Figure 5 to minimize the residual stresses, variable A (Filling time) must be as low as possible, 0 s., however, since the filling time cannot have a zero value it is more realistic to have 1s. as filling time, variable B (Switch to pack percentage) must be as high as possible, thus the selected value for variable B is 80%, variable C (Pressure holding time) must be as high as possible, thus 11s, as pressure holding time will be selected, variable D (Cooling time) must be as high as possible, thus 16s, as cooling time will be selected, and variable E (Pressure holding magnitude) must be as low as possible, thus 35 MPa will be selected.
The optimal combination discussed above (Filling time, 1s; Switch to pack percentage, 80%; Pressure holding time, 11s; Cooling time, 16s; and Holding pressure magnitude, 35 MPa) was verified and it gave residual stresses of 7.0125 MPa.
The optimal value for the residual stresses obtained using TED was 13.3111 MPa; however, the optimal value for the residual stresses obtained using RSM was 7.0125 MPa. It is known that TED is not capable for global optimization and it excludes the interactions among variables; on the contrary the RSM is capable for global optimization as well as revealing the interactions among variables.
5. Conclusions
The suggested model building stage for the injection molding included a screening stage to reduce the number of variables included in the modeling stage. This has direct effects on the number of experiments and the modeling cost. It actively reduced the number of input variables from 8 to 5 and the number of Response surface experiments from 160 to 56. Filling time, switch to pack percentage, pressure holding time, holding pressure magnitude, and cooling time are found to be the significant factors. The best subset and verification based model selection was successful in building a model with a verification result of nearly 0.93.
There was a controversial difference in optimal behavior between the Taguchi stage (Phase 1) and Response Surface stage (Phase 2). With the expectation of the Response Surface stage, the outperforming Taguchi expectations definitely justifies the phase 2 suggested in this work.
Cite this paper
FaisalAlkaabneh,MahmoudBarghash,YousefAbdullat, (2016) A Novel Statistical Analysis for Residual Stress in Injection Molding. American Journal of Operations Research,06,90-103. doi: 10.4236/ajor.2016.61012
References
- 1. Chen, X., Lam, Y.C. and Li, D.Q. (2000) Analysis of Thermal Residual Stress in Plastic Injection Molding. Journal of Materials Processing Technology, 101, 275-280.
http://dx.doi.org/10.1016/S0924-0136(00)00472-6 - 2. Kurt, M., Kamber, S., Kaynak, Y., Atakok, G. and Girit, O. (2009) Experimental Investigation of Plastic Injection Molding: Assessment of the Effects of Cavity Pressure and Mold Temperature on the Quality of the Final Products. Materials and Design, 30, 3217-3124.
http://dx.doi.org/10.1016/j.matdes.2009.01.004 - 3. Hassan, H., Regnier, N., Pujos, C., Arquis, E. and Defaye, G. (2010) Modeling the Effect of Cooling System on the Shrinkage and Temperature of the Polymer by Injection Molding. Applied Thermal Engineering, 30, 1547-1557.
http://dx.doi.org/10.1016/j.applthermaleng.2010.02.025 - 4. Oktem, H., Erzurumlu, T. and Uzman, I. (2007) Application of Taguchi Optimization Technique in Determining Plastic Injection Molding Process Parameters for a Thin Shell Part. Materials and Design, 28, 1271-1278.
http://dx.doi.org/10.1016/j.matdes.2005.12.013 - 5. Chiang, K.-T. and Chang, F.-P. (2006) Application of Grey-Fuzzy Logic on the Optimal Process Design of an Injection-Molded Part with a Thin Shell Feature. International Communications in Heat and Mass Transfer, 33, 94-101.
http://dx.doi.org/10.1016/j.icheatmasstransfer.2005.08.006 - 6. Ozcelik, B. and Erzurumlu, T. (2005) Determination of Effecting Dimensional Parameters on Warpage of Thin Shell Plastic Parts Using Integrated Response Surface Method and Genetic Algorithm. International Communications in Heat and Mass Transfer, 32, 1085-1094.
http://dx.doi.org/10.1016/j.icheatmasstransfer.2004.10.032 - 7. Barghash, M.A. and Alkaabneh, F.A. (2014) Shrinkage and Warpage Detailed Analysis and Optimization for the Injection Molding Process Using Multistage Experimental Design. Quality Engineering, 26, 319-334.
http://dx.doi.org/10.1080/08982112.2013.852679 - 8. Kim, C-H. and Youn, J-R. (2007) Determination of Residual Stresses in Injection-Moulded Flat Plate: Simulation and Experiments. Polymer Testing, 26, 862-868.
http://dx.doi.org/10.1016/j.polymertesting.2007.05.006 - 9. Choi, D.-S. and Im, Y.-T. (1999) Prediction of Shrinkage and Warpage in Consideration of Residual Stress in Integrated Simulation of Injection Molding. Composite Structures, 47, 655-665.
http://dx.doi.org/10.1016/S0263-8223(00)00045-3 - 10. Wang, T.-H. and Young, W.-B. (2005) Study on Residual Stresses of Thin-Walled Injection Molding. European Polymer Journal, 41, 2511-2517.
http://dx.doi.org/10.1016/j.eurpolymj.2005.04.019 - 11. Kamal, M., Lai-Fook, R. and Hernandez-Aguilar, J. (2002) Residual Thermal Stresses in Injection Moldings of Thermoplastics: A Theoretical and Experimental Study. Polymer Engineering & Science, 42, 1098-1114.
http://dx.doi.org/10.1002/pen.11015 - 12. Mathivanan, D. and Parthasarathy, N.-S. (2009) Sink-Mark Minimization in Injection Molding through Response Surface Regression Modeling and Genetic Algorithm. International Journal of Advanced Manufacturing Technology, 45, 867-874.
http://dx.doi.org/10.1007/s00170-009-2021-z - 13. Changyu, S., Lixia, W. and Qian, L. (2007) Optimization of Injection Molding Process Parameters Using Combination of Artificial Neural Network and Genetic Algorithm Method. Journal of Materials Processing Technology, 183, 412-418.
http://dx.doi.org/10.1016/j.jmatprotec.2006.10.036 - 14. Zhao, P., Zhou, H., Li, Y. and Li, D. (2010) Process Parameters Optimization of Injection Molding Using a Fast Strip Analysis as a Surrogate Model. International Journal of Advanced Manufacturing Technology, 49, 949-959.
http://dx.doi.org/10.1007/s00170-009-2435-7 - 15. Park, K. and Ahn, J. (2004) Design of Experiment Considering Two-Way Interactions and Its Application to Injection Molding Processes with Numerical Analysis. Journal of Materials Processing Technology, 146, 221-227.
http://dx.doi.org/10.1016/j.jmatprotec.2003.10.020 - 16. Chen, C.-P., Chuang, M.-T., Hsiao, Y.-H., Yang, Y.-K. and Tsai, C.-H. (2009) Simulation and Experimental Study in Determining Injection Molding. Expert Systems with Applications, 36, 10752-10759.
http://dx.doi.org/10.1016/j.eswa.2009.02.017 - 17. AlKaabneh, F.A., Barghash, M. and Mishael, I. (2013) A Combined Analytical Hierarchical Process (AHP) and Taguchi Experimental Design (TED) for Plastic Injection Molding Process Settings. The International Journal of Advanced Manufacturing Technology, 66, 679-694.
- 18. Erzurumlu, T. and Ozcelik, B. (2006) Minimization of Warpage and Sink Index in Injection Molded Thermoplastic Parts Using Taguchi Optimization Method. Materials and Design, 27, 853-861.
http://dx.doi.org/10.1016/j.matdes.2005.03.017 - 19. Ozcelik, B., Ozbay, A. and Demirbas, E. (2010) Influence of Injection Parameters and Mold Materials on Mechanical Properties of ABS in Plastic Injection Molding. International Communications in Heat and Mass Transfer, 37, 1359-1365.
http://dx.doi.org/10.1016/j.icheatmasstransfer.2010.07.001 - 20. Taguchi, G. (1990) Introduction to Quality Engineering. McGraw-Hill, New York.
- 21. Liao, S., Hsieh, W., Wang, J. and Su, Y. (2004) Shrinkage and Warpage Prediction of Injection-Molded Thin-Wall Parts Using Artificial Neural Networks. Polymer Engineering and Science, 44, 2029-2040.
http://dx.doi.org/10.1002/pen.20206 - 22. Lin, B.-T., Jean, M.-D. and Chou, J.-H. (2007) Using Response Surface Methodology for Optimizing Deposited Partially Stabilized Zirconia in Plasma Spraying. Applied Surface Science, 253, 3254-3262.
http://dx.doi.org/10.1016/j.apsusc.2006.07.021 - 23. Chen, C.-C., Su, P.-L. and Lin, Y.-C. (2009) Analysis and Modeling of Effective Parameters for Dimension Shrinkage Variation of Injection Molded Part with Thin Shell Feature Using Response Surface Methodology. International Journal of Advanced Manufacturing Technology, 45, 1087-1095.
http://dx.doi.org/10.1007/s00170-009-2045-4 - 24. Postawa, P. and Koszkul, J. (2005) Change in Injection Moulded Parts Shrinkage and Weight as a Function of Processing Conditions. Journal of Materials Processing Technology, 162, 109-115.
http://dx.doi.org/10.1016/j.jmatprotec.2005.02.241 - 25. Palardy, G., Hubert, P., Haider, M. and Lessard, L. (2008) Optimization of RTM Processing Parameters for Class A Surface Finish. Composites: Part B, 39, 1280-1286.
http://dx.doi.org/10.1016/j.compositesb.2007.12.003 - 26. Simpoe Mesh Version 3.0.
- 27. Minitab 15, MINITAB Inc., 2007.
- 28. Simpoe-Mold 2011 R2.0.
- 29. Fung, C.-P. and Kang, P.-C. (2005) Multi-Response Optimization in Friction Properties of PBT Composites Using Taguchi Method and Principle Component Analysis. Journal of Materials Processing Technology, 170, 602-610.
http://dx.doi.org/10.1016/j.jmatprotec.2005.06.040 - 30. Chiang, K.-T. and Chang, F.-P. (2007) Analysis of Shrinkage and Warpage in an Injection-Molded Part with a Thin Shell Feature Using the Response Surface Methodology. International Journal of Advanced Manufacturing Technology, 35, 468-479.
http://dx.doi.org/10.1007/s00170-006-0739-4 - 31. Mallows, C.L. (1973) Some Comments on CP. Technometrics, 15, 661-675.






