American Journal of Operations Research
Vol.3 No.6(2013), Article ID:40055,11 pages DOI:10.4236/ajor.2013.36054
A Two Stage Batch Arrival Queue with Reneging during Vacation and Breakdown Periods
1Brunel Business School, Brunel University, London, UK
2College of Information Technology, Ahlia University, Manama, Bahrain
Email: *Monita.Baruah@brunel.ac.uk, monitabrh@gmail.com, kmadan@ahlia.edu.bh, Tillal.Eldabi@brunel.ac.uk
Copyright © 2013 Monita Baruah et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 30, 2013; revised October 30, 2013; accepted November 7, 2013
Keywords: Two-Stage Service; Batch Arrivals; Breakdowns; Reneging; Steady State Queue Size
ABSTRACT
We study a two stage queuing model where the server provides two stages of service one by one in succession. We consider reneging to occur when the server is unavailable during the system breakdown or vacation periods. We concentrate on deriving the steady state solutions by using supplementary variable technique and calculate the mean queue length and mean waiting time. Further some special cases are also discussed and numerical examples are presented.
1. Introduction
Queues with impatient customers have attracted the attention of many researchers and we see significant contribution by numerous researchers in this area. One of the earliest works on balking and reneging was by Haight [1,2], Barrer [3], was the first to introduce reneging where he studied deterministic reneging with single server markovian arrival and service rates. Another early work on markovian reneging with markovian and arrival and service pattern was by Ancker and Gafarian [4], Haghighi et al. [5] studied a markovian multiserver queuing system with balking and reneging. Consequently, we see a lot of developments in the study of queues with impatient customers in recent years. An M/G/1 queue with deterministic reneging was studied by Bae et al. [6]. We refer to some authors like Zhang et al. [7], El-Pauomy [8], Altman and Yechiali [9,10], Kumar and Sharma [11] who studied queues with impatient customers in different contexts.
Vacation queues are an important area in the literature of queuing theory. Since the past two decades it has emerged as an important area of study due to its various applicability in real life problems such as telecommunication engineering, manufacturing and production industries, computer and communication networks etc. A few of early works on queues with vacations are seen by authors like Levy and Yechailai [12], Doshi [13], Keilson and Servi [14]. A two stage batch arrival queuing system where customers receive a batch service in the first and individual service in the second stage was studied by Doshi [15] in the past. In recent years, extensive amount of work has been done on batch arrival queues with vacations and breakdowns. We mention a few recent papers by Kumar and Arumuganathan [16], Choudhury, Tadj and Paul [17], Maraghi, Madan and Darby-Dowman [18], Khalaf, Madan and Lukas [19].
In this paper we consider a batch arrival queue where service is offered in two stages of service, one by one in succession. We extend and develop this model by adding new assumptions reneging and system breakdowns. Customers may renege (leave the queue after joining) during server breakdowns or during the time when the server takes vacation due to impatience. This is a very realistic assumption and often we come across such queuing situations in the real world.
2. The Mathematical Model
a) Customers arrive in batches following a compound Poisson Process with rate of arrival λ.
Let 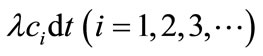 be the first order probability that customers arrive at the system in batches of size i, at the system at a short interval of time
be the first order probability that customers arrive at the system in batches of size i, at the system at a short interval of time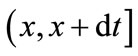 , where
, where
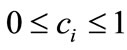 and
and 
b) The server provides two stages of heterogeneous services one after the other in succession. An arrival batch shall receive the service offered at two stages one by one in succession, defined as the first stage (FS) and second stage (SS) service respectively. The service discipline is assumed to be on a first come first served basis (FCFS).
We assume that the service time Sj (j = 1, 2) of the jth stage service follows a general probability distribution with distribution function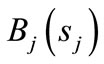 ,
, 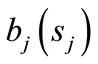 being the probability density function and
being the probability density function and 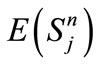 as the nth moment of the service time, j = 1,2 Let
as the nth moment of the service time, j = 1,2 Let 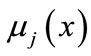 be the conditional probability of stage j service during the period
be the conditional probability of stage j service during the period 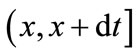 given elapsed time is x such that
given elapsed time is x such that
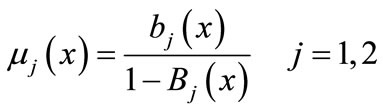 (1)
(1)
and
 (2)
(2)
c) Once the second stage service (SS) of a unit is complete the server is assumed to take vacation with probability p or may continue to offer service with probability . As soon as the vacation period of the server is over, he joins the system to continue service of the waiting customers.
. As soon as the vacation period of the server is over, he joins the system to continue service of the waiting customers.
We assume the vacation time to be a random variable following general probability law with distribution function given by 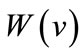 and density function by
and density function by 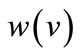 and
and 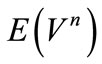 is the nth moment
is the nth moment  of vacation time. Here we assume that
of vacation time. Here we assume that 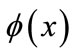 be the conditional probability of a vacation period during the interval
be the conditional probability of a vacation period during the interval , given that elapsed time is x, so that
, given that elapsed time is x, so that
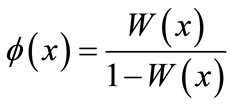 (3)
(3)
and thus
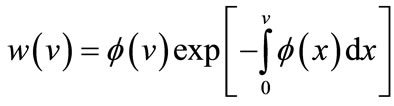 (4)
(4)
d) In addition, customers arriving for service may become impatient and renege (leave the queue) after joining during vacations and breakdown periods. Reneging is assumed to follow exponential distribution with parameter γ. Thus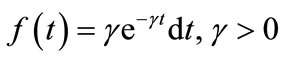 . Thus
. Thus 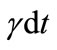 is the probability that a customer can renege during a short interval of time
is the probability that a customer can renege during a short interval of time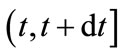 .
.
The system may fail or be subjected to breakdown at random. The customer receiving service during breakdown returns back to the head of the queue. We assume that time between breakdowns occur according to a Poisson process with mean rate of breakdown as . Further the repair times follows a general (arbitrary) distribution with distribution function F(x) and density function f(x). Let the conditional probability of completion of the repair process is β(x)dx such that
. Further the repair times follows a general (arbitrary) distribution with distribution function F(x) and density function f(x). Let the conditional probability of completion of the repair process is β(x)dx such that 
and thus 
3. Definitions and Notations
We assume that steady state exists and define 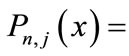 Probability that there are n (≥1) customers in the system including one customer in type j service, j =1,2 and elapsed service time is x. Thus
Probability that there are n (≥1) customers in the system including one customer in type j service, j =1,2 and elapsed service time is x. Thus 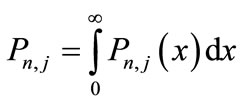 is the corresponding steady state probability irrespective of elapsed time x.
is the corresponding steady state probability irrespective of elapsed time x.
 = probability that there are n (≥0) customers in the queue and server is on vacation and elapsed vacation time is x.
= probability that there are n (≥0) customers in the queue and server is on vacation and elapsed vacation time is x. 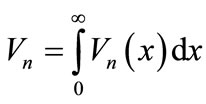 is the corresponding steady state probability irrespective of elapsed vacation time x.
is the corresponding steady state probability irrespective of elapsed vacation time x.
 Steady state probability of the server is idle as the server takes vacation The Probability Generating Functions are defined as:
Steady state probability of the server is idle as the server takes vacation The Probability Generating Functions are defined as:
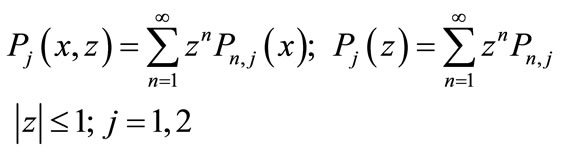 (5)
(5)
 (6)
(6)
 (7)
(7)
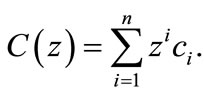 (8)
(8)
4. Equations Governing the System
Under this model we construct the differential equations as
 (9)
(9)
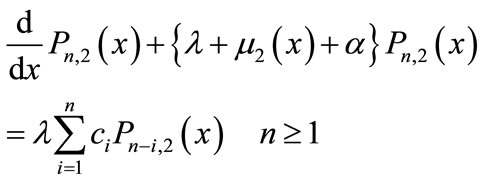 (10)
(10)
 (11)
(11)
 (12)
(12)
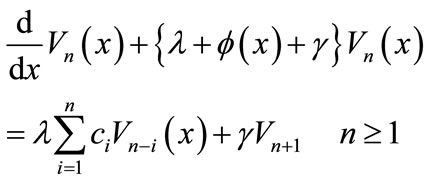 (13)
(13)
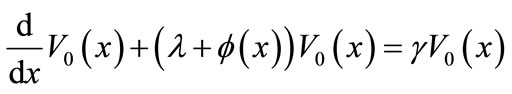 (14)
(14)
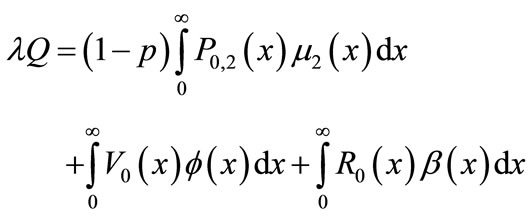 (15)
(15)
The above differential equations now have to be solved subject to the following boundary conditions:
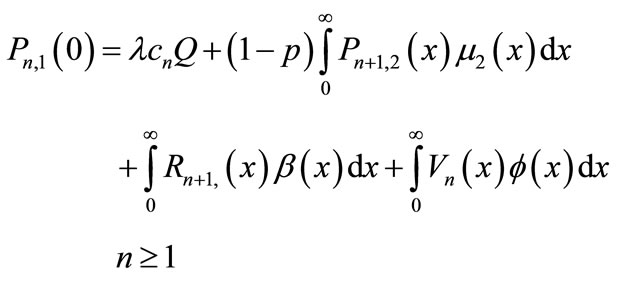 (16)
(16)
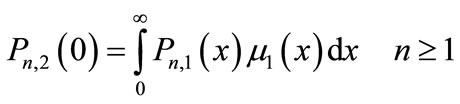 (17)
(17)
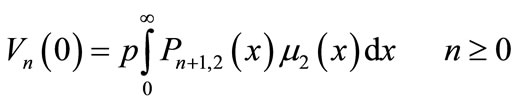 (18)
(18)
 (19)
(19)
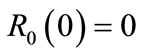 (20)
(20)
5. Queue Size Distribution at Random Epoch
Multiplying Equations (9) and (10) by 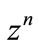 and summing over n from 1 to ∞, yields
and summing over n from 1 to ∞, yields
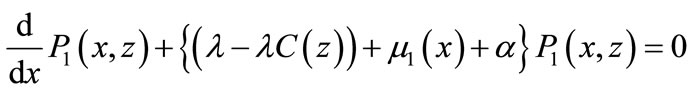 (21)
(21)
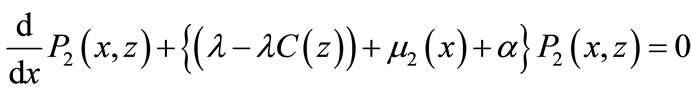 (22)
(22)
Applying the same process in Equation (11) and using (12) gives
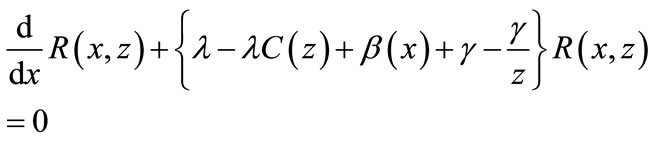 (23)
(23)
Similarly from (13) and (14), we get
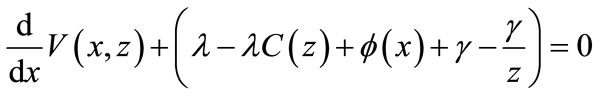 (24)
(24)
Further integrating Equations (21)-(24) over limits 0 to x gives us the following
 (25)
(25)
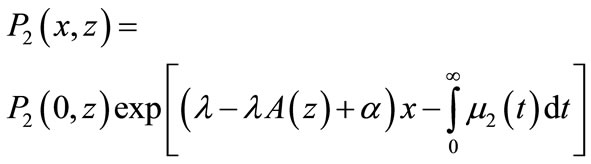 (26)
(26)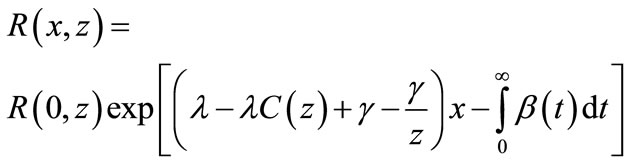 (27)
(27)
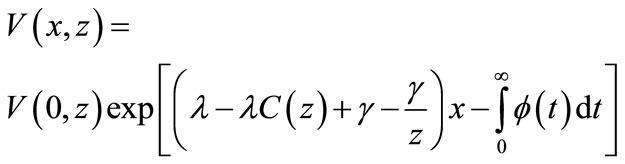 (28)
(28)
Next multiplying the boundary conditions by suitable powers of zn+1 and taking summation over all possible values of n and using the PGF’s we get after simplification
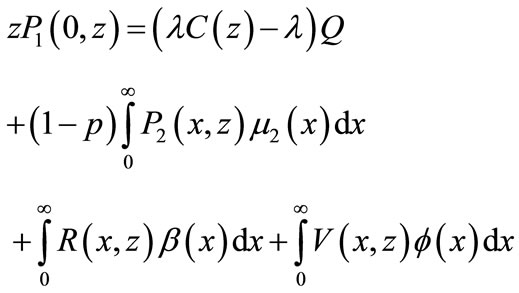 (29)
(29)
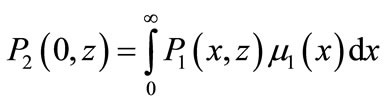 (30)
(30)
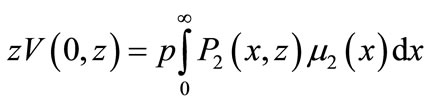 (31)
(31)
Now multiplying Equation (19) by zn+1, summing over n from 0 to ∞, and using (20) and PGF’s we have
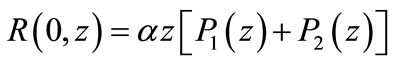 (32)
(32)
Again integrating Equations (25)-(28) with respect to x, gives us
 (33)
(33)
 (34)
(34)
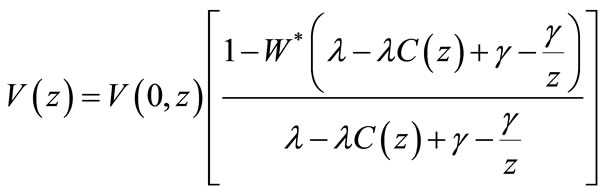 (35)
(35)
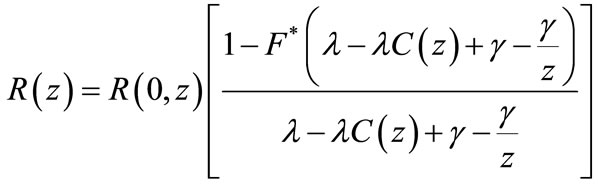 (36)
(36)
where

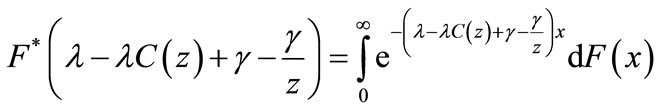
and
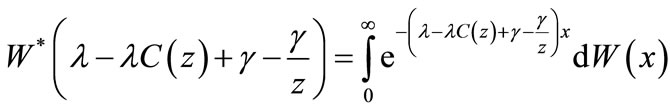
are the Laplace-Steiltjes transform of the first stage service time, second stage service time, repair time and vacation time respectively.
Now we determine the integrals

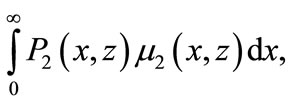
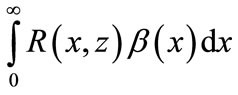
and
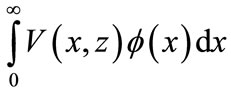
by multiplying the RHS of Equations (25)-(28) by  and
and 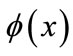 respectively and integrate with respect to x and obtain
respectively and integrate with respect to x and obtain
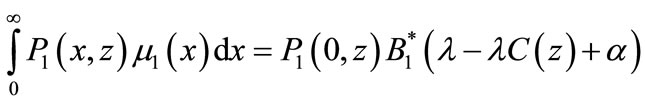 (37)
(37)
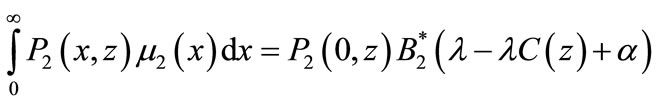 (38)
(38)
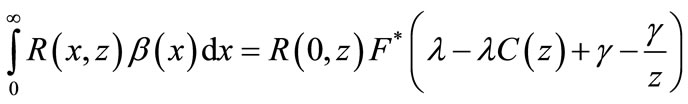 (39)
(39)
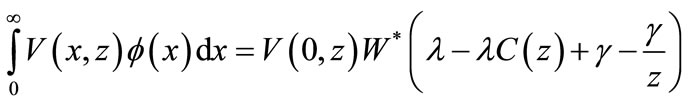 (40)
(40)
Let us take
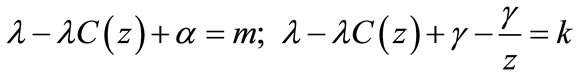
Utilizing (37)-(40) in Equations (29)-(31) we obtain
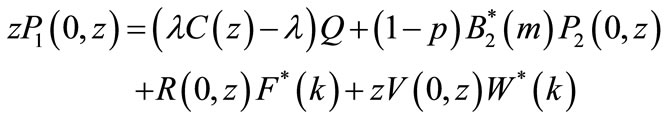 (41)
(41)
 (42)
(42)
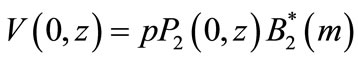 (43)
(43)
Using (42) in (43) we get,
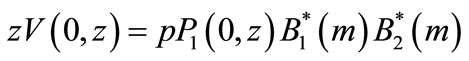 (44)
(44)
Again from (32) using (33) and (34) we get
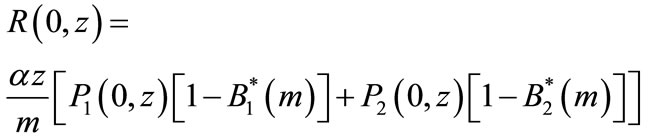 (45)
(45)
Now using (42), (44) and (45) in Equation (41), we solve for 
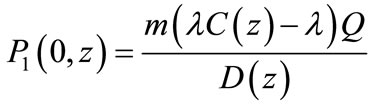 (46)
(46)
and
 (47)
(47)
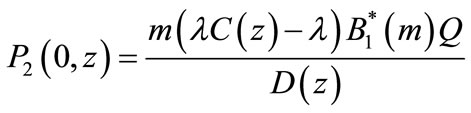 (48)
(48)
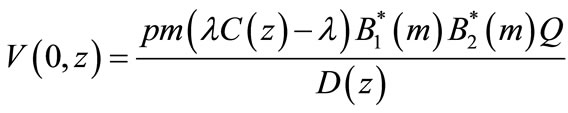 (49)
(49)
Substituting the values from (46), (48) and (49) in (33)-(36), we obtain
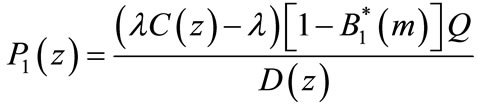 (50)
(50)
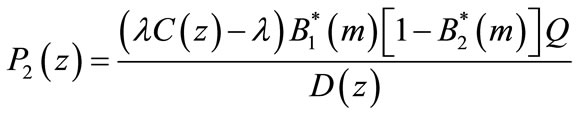 (51)
(51)
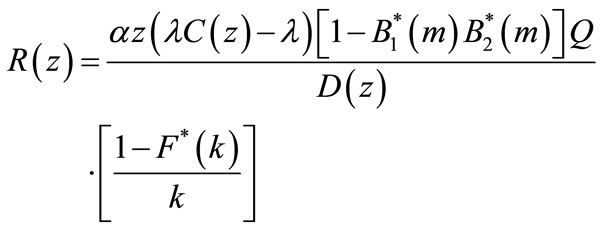 (52)
(52)
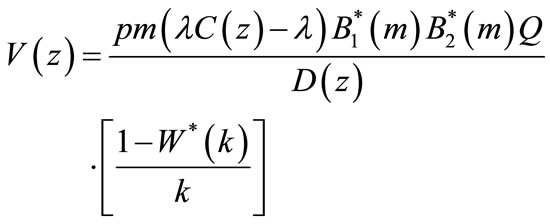 (53)
(53)
Let 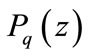 denote the probability generating function of the queue size irrespective of the state of the system.
denote the probability generating function of the queue size irrespective of the state of the system.
 (54)
(54)
In order to determine the probability of idle time we use the normalizing condition
we use the normalizing condition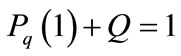 . Again since (51) is indeterminate of the form 0/0 at z = 1, we use L’Hopital’s Rule on Equation (51) to obtain
. Again since (51) is indeterminate of the form 0/0 at z = 1, we use L’Hopital’s Rule on Equation (51) to obtain
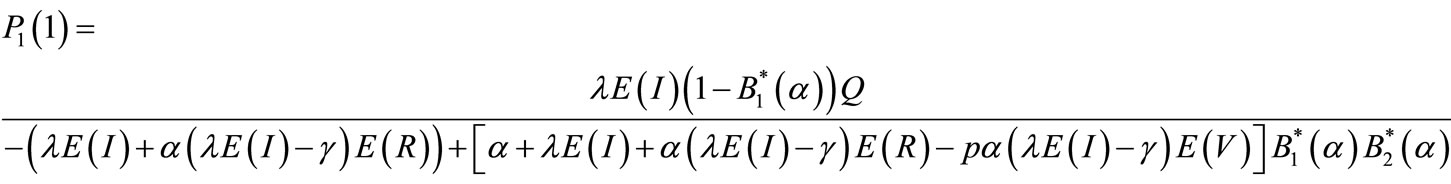 (55)
(55)
(55) is the steady state probability that server is providing service in stage 1.
The steady state probability that server is providing service in stage two is
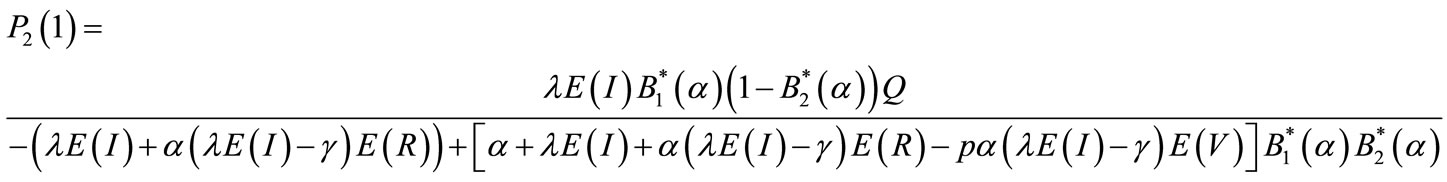 (56)
(56)
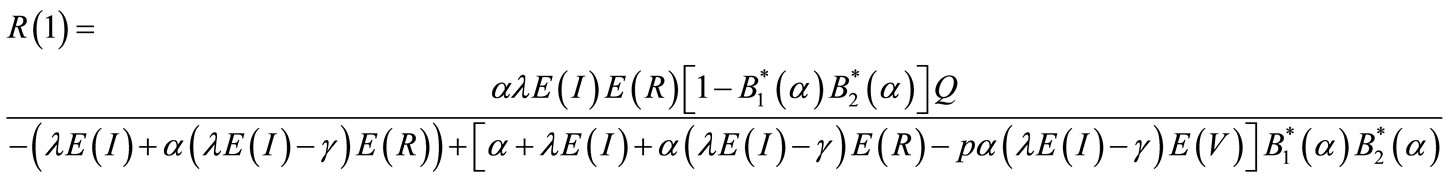 (57)
(57)
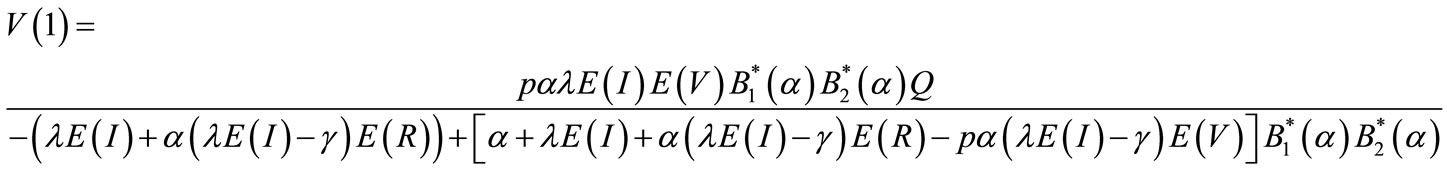 (58)
(58)
where 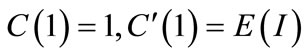 is the mean of arriving batch of customers,
is the mean of arriving batch of customers,  is the mean repair time and
is the mean repair time and 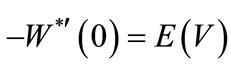 is the mean vacation time.
is the mean vacation time.
Thus the normalization condition yields
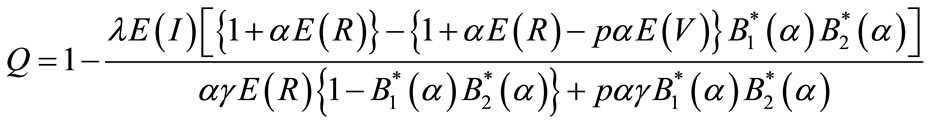 (59)
(59)
And therefore the traffic intensity (utilization factor) 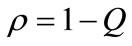 is
is
 (60)
(60)
6. Average Queue Size and Average Waiting Time
Since , the mean queue size is of the 0/0 form, we apply L’Hopital’s Rule twice and obtain
, the mean queue size is of the 0/0 form, we apply L’Hopital’s Rule twice and obtain
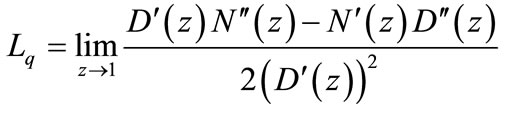 (61)
(61)
where primes and double primes denote the first and second derivatives respectively.
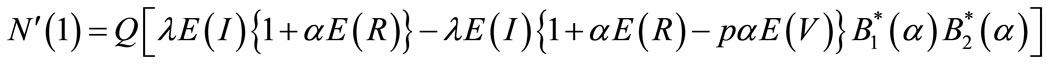 (62)
(62)
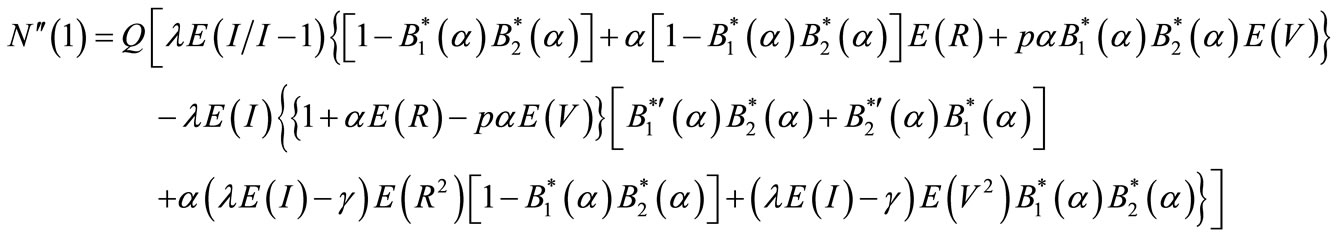 (63)
(63)
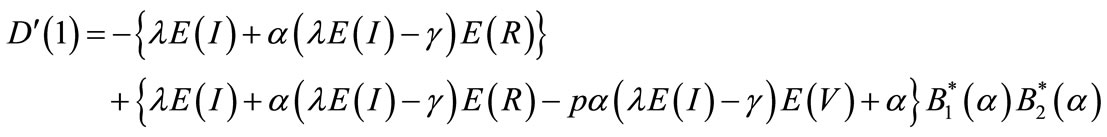 (64)
(64)
 (65)
(65)
where Q is given by (59), F" = E(R2), W" = E(V2) are the second moments of repair time and vacation time respectively, and  is the second factorial moment of batch of arriving customers. Hence utilizing (62)-(65) in (61), we can obtain the mean length of queue size at random epoch
is the second factorial moment of batch of arriving customers. Hence utilizing (62)-(65) in (61), we can obtain the mean length of queue size at random epoch 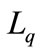 and the mean waiting time of the queue
and the mean waiting time of the queue  can be obtained by using
can be obtained by using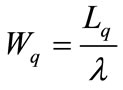 . Alternatively, we can find
. Alternatively, we can find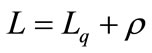 , the mean queue size of the system and
, the mean queue size of the system and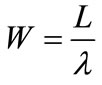 , the mean waiting time in the system.
, the mean waiting time in the system.
7. Special Cases
7.1. Case 1. No Server Vacations
In this case, the server has no option to take a vacation. Hence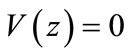 . Thus letting
. Thus letting 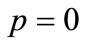 in our results (50)-(52), we obtain the following and our model reduces to a two stage batch arrivals with reneging during breakdowns.
in our results (50)-(52), we obtain the following and our model reduces to a two stage batch arrivals with reneging during breakdowns.
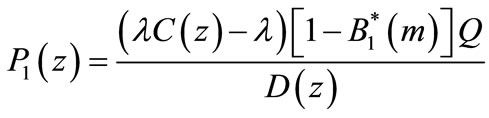 (66)
(66)
 (67)
(67)
 (68)
(68)
and
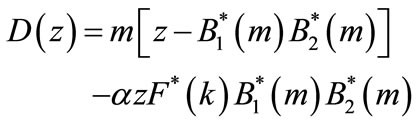 (69)
(69)
The probability of idle time is
 (70)
(70)
And the traffic intensity 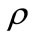 is
is
 (71)
(71)
Further putting  in the Equations (62)-(65) we can obtain the mean queue size
in the Equations (62)-(65) we can obtain the mean queue size 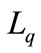 and mean waiting time
and mean waiting time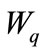 .
.
7.2. Case 2. No Reneging
In this case we consider that customers do not renege during breakdowns and vacations. So we let the parameter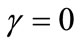 . Then
. Then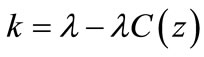 . Then our model reduces to a two stage batch arrival queuing system with vacations and breakdowns. Thus Equations (50)-(53) changes to
. Then our model reduces to a two stage batch arrival queuing system with vacations and breakdowns. Thus Equations (50)-(53) changes to
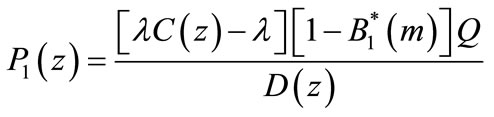 (72)
(72)
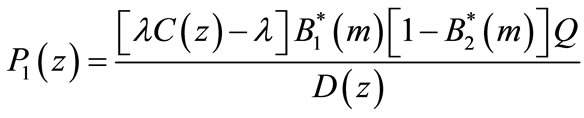 (73)
(73)
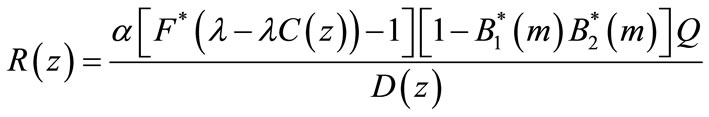 (74)
(74)
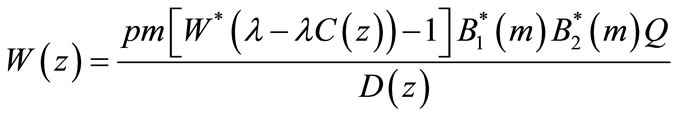 (75)
(75)
where

The probability of idle time Q
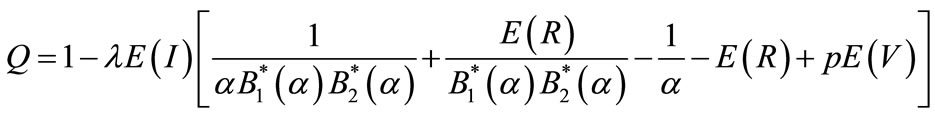 (76)
(76)
And the utilization factor is
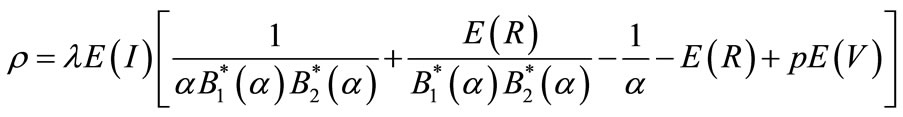 (77)
(77)
The result (72)-(75) agrees with the result obtained by Margahi, Madan and Darby-Dowman for a Batch arrival queue with two stage Heterogeneous service, Bernoulli schedule vacations and general repair times.
7.3. Case 3: No System Breakdowns and No Reneging
In this case, the server does not face any breakdown and there is also reneging of customers. So we take 
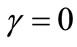 in our Equations (50)-(53). Then
in our Equations (50)-(53). Then 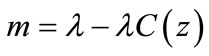 and
and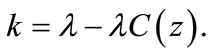 .
.
Thus we have
 (78)
(78)
 (79)
(79)
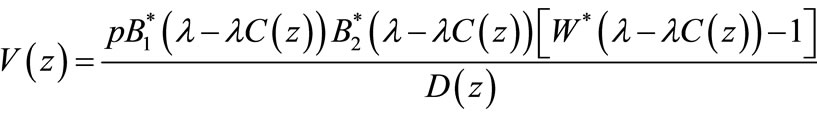 (80)
(80)
where
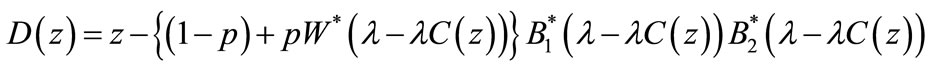
The probability generating function of the queue size takes the form
 (81)
(81)
The probability of idle time Q is

and the traffic intensity is

Thus (81) gives the steady state queue size of a  vacation queue, i.e. a two stage batch arrival vacation queue.
vacation queue, i.e. a two stage batch arrival vacation queue.
7.4. Case 4: Exponential Service Time and Exponential Vacation Time
In this case we assume that the service time for the two stages of service with service rate , and
, and , respectively are exponentially distributed. Further the repair time and vacation are all exponentially distributed with repair rate
, respectively are exponentially distributed. Further the repair time and vacation are all exponentially distributed with repair rate  and vacation rate ϕ > 0.
and vacation rate ϕ > 0.
Thus
 (82)
(82)
where
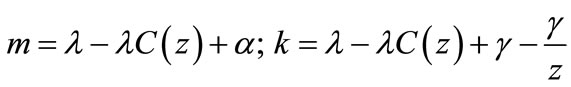
Utilizing the above relations in Equations (50)-(53), we obtain
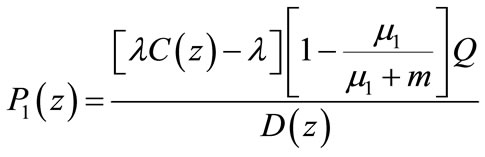 (83)
(83)
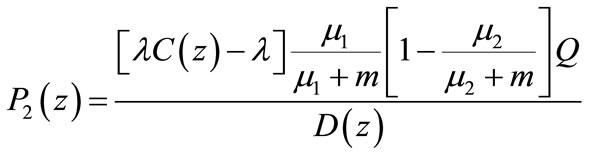 (84)
(84)
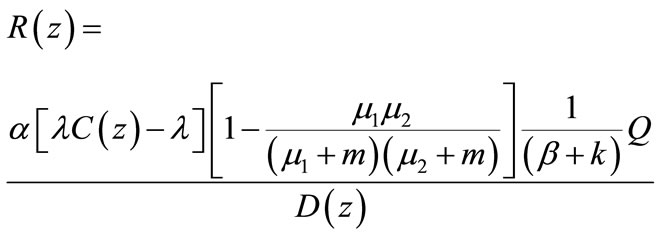 (85)
(85)
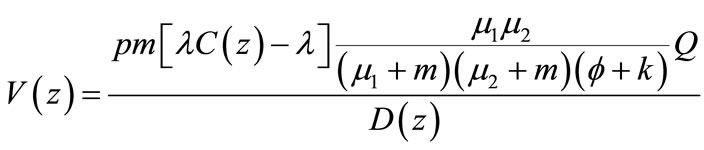 (86)
(86)
where
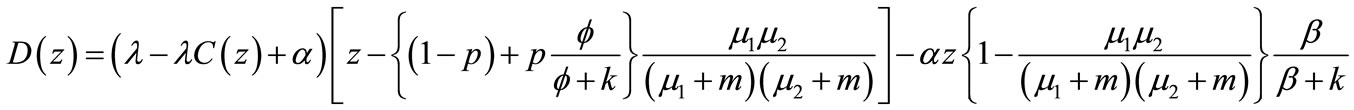
Therefore the probability that the server is providing service in first stage at random point of time is
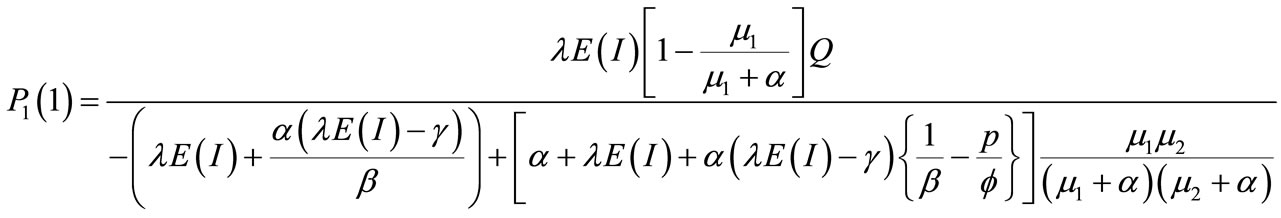 (87)
(87)
Probability that server is providing service in second stage at random point of time is
 (88)
(88)
Probability that the server is under repairs at random point of time is
 (89)
(89)
And probability that server is on vacation at random point of time is given by
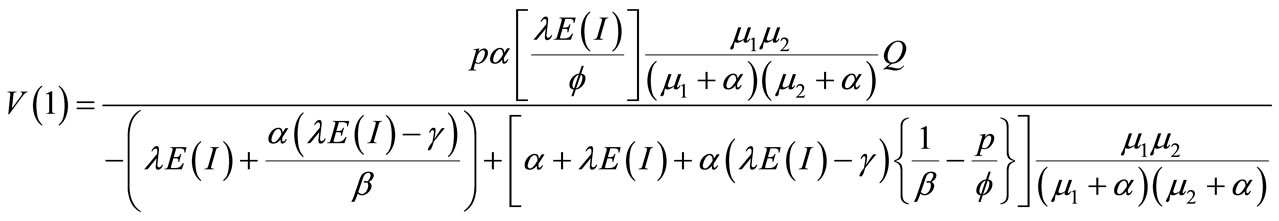 (90)
(90)
Probability that the server is idle but available in the system is
 (91)
(91)
Similarly the mean queue size and mean waiting time can be derived by finding 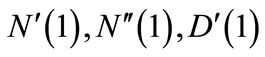 and
and 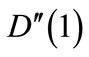 and utilizing in Equation (61).
and utilizing in Equation (61).

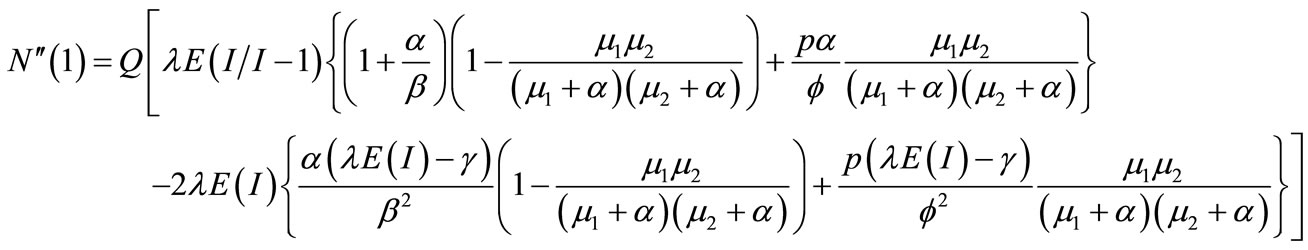

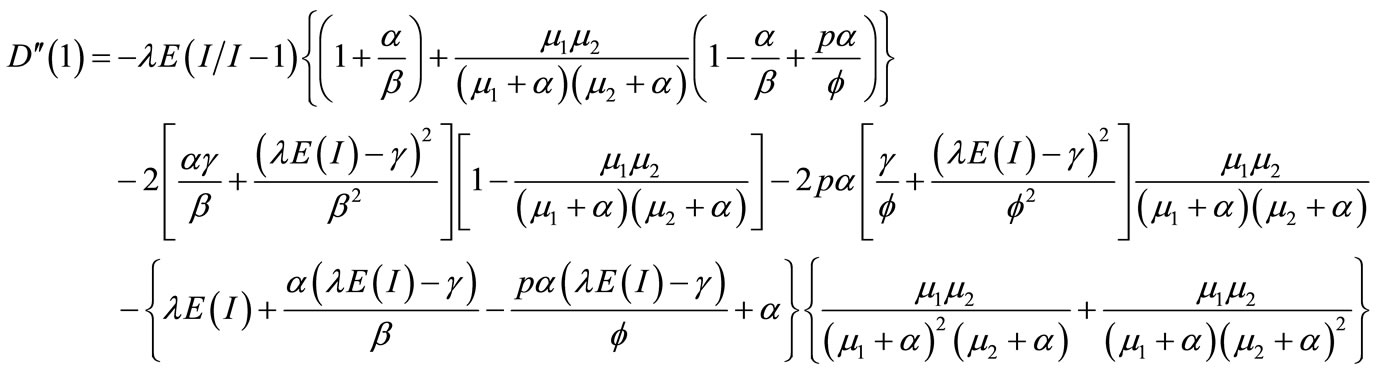
8. Numerical Illustration
In order to see the effect of different parameters especially the reneging and breakdown parameter on the different states of the server, the utilization factor and proportion of idle time, we compute some numerical results. We consider the service time, vacation time and repair time to be exponentially distributed to numerically illustrate the feasibility of our results. Further we assume that arrivals come one by one, i.e.  and
and  with arrival rate
with arrival rate , first stage service rate
, first stage service rate 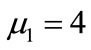 and second stage service rate
and second stage service rate 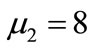
All the parameters are selected such that the steady state condition is satisfied.
To monitor the effect of the reneging 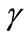 and breakdown
and breakdown 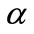 on the behavior of the queuing model, we take
on the behavior of the queuing model, we take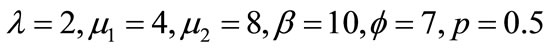 , while
, while 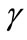 varies from 5, 8, 9 and
varies from 5, 8, 9 and 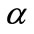 varies from 1 to 4, in Table 1.
varies from 1 to 4, in Table 1.
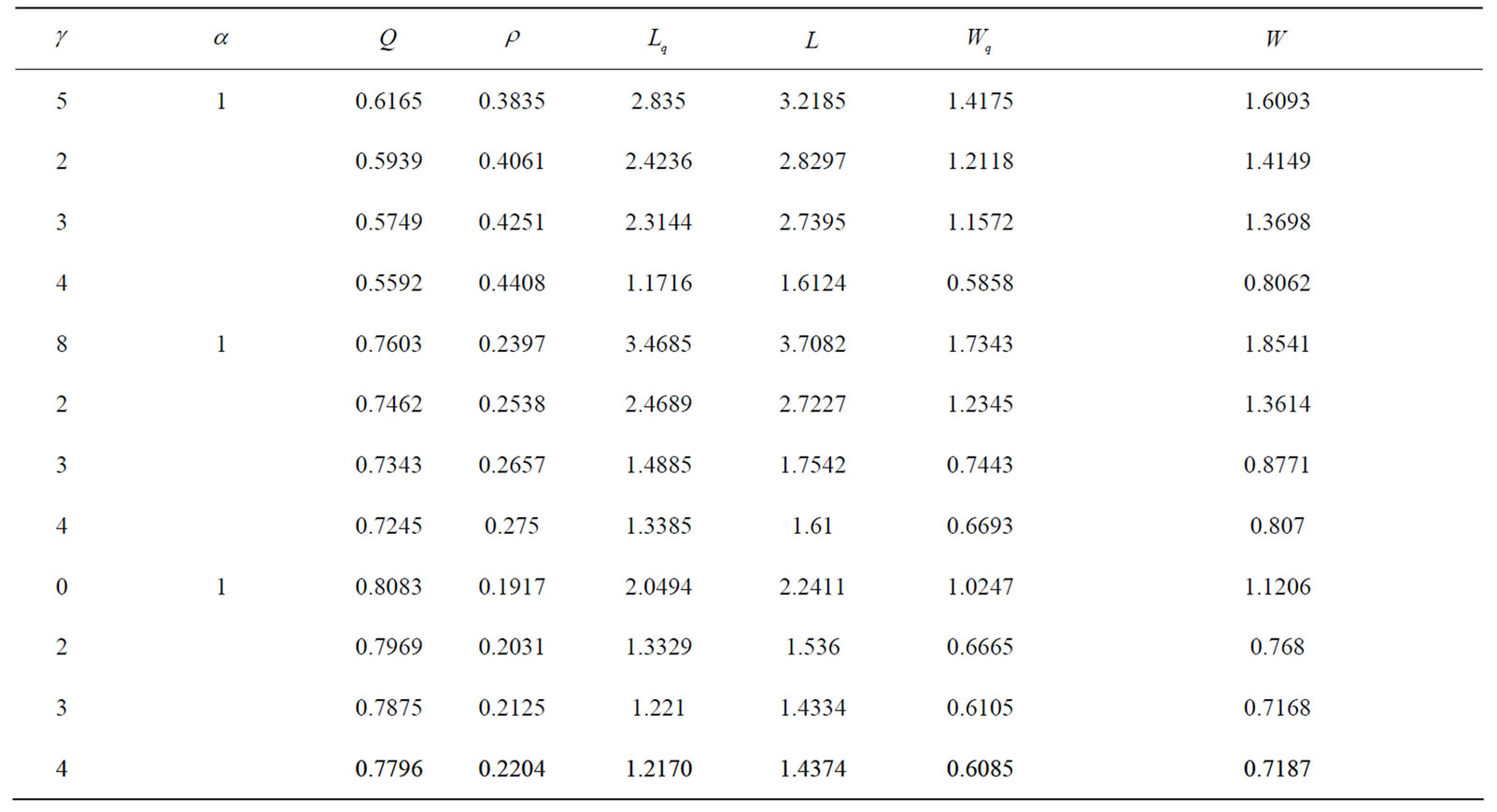
Table 1. Computing measures of queue characteristics when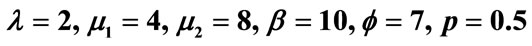 .
.
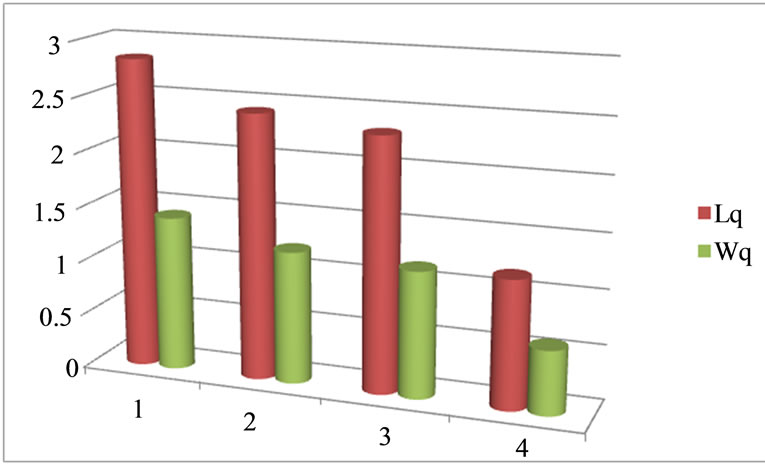
Figure 1. Effect of  and
and 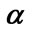 on the mean queue size
on the mean queue size  and mean waiting time
and mean waiting time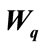 .
.

Figure 2. Effect of 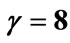 and
and  on the mean queue size
on the mean queue size 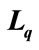 and mean waiting time
and mean waiting time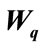 .
.
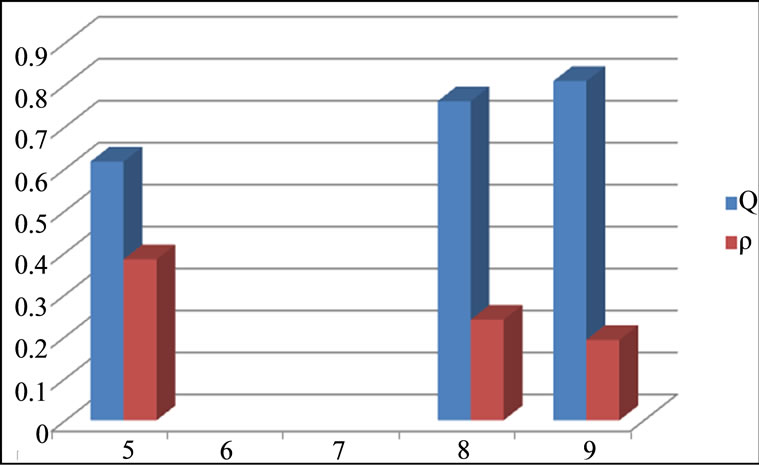
Figure 3. Effect of reneging 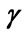 and breakdown at
and breakdown at 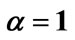 on the proportion of idle time Q and utilization factor
on the proportion of idle time Q and utilization factor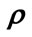 .
.
Thus from Table 1, we observe that as we increase the parameter of customer’s impatience reneging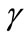 , for varying values of breakdown parameter
, for varying values of breakdown parameter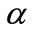 , the utilization factor decreases, while the probability of server idle time increases. Figures 1 and 2 show the effect of reneging and breakdown on the mean queue size
, the utilization factor decreases, while the probability of server idle time increases. Figures 1 and 2 show the effect of reneging and breakdown on the mean queue size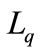 , mean waiting time
, mean waiting time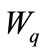 . It is clear that as breakdown occurs, it increases the average length of queue and due to customers reneging from the queue, the average waiting time also decreases. Again from Figure 3, it is clear that due to breakdown of the system and reneging, the proportion of idle time of the server increases and utilization factor or busy period decreases. The trends shown by the above table are as expected.
. It is clear that as breakdown occurs, it increases the average length of queue and due to customers reneging from the queue, the average waiting time also decreases. Again from Figure 3, it is clear that due to breakdown of the system and reneging, the proportion of idle time of the server increases and utilization factor or busy period decreases. The trends shown by the above table are as expected.
REFERENCES
- F. A. Haight, “Queueing with Balking,” Biometrika, Vol. 44, No. 3-4, 1957, pp. 360-369. http://dx.doi.org/10.2307/2332868
- F. A. Haight, “Queueing with Reneging,” Metrika, Vol. 2, No. 1, 1959, pp. 186-197. http://dx.doi.org/10.1007/BF02613734
- D. Y. Barrer, “Queueing with Impatient Customers and Ordered Service,” Operation Research, Vol. 5, No. 5, 1957, pp. 650-656. http://dx.doi.org/10.1287/opre.5.5.650
- C. J. Ancker Jr. and A. V. Gafarian, “Some Queuing Problems with Balking and Reneging,” Operations Research, Vol. 11, No. 1, 1963, pp. 88-100. http://dx.doi.org/10.1287/opre.11.1.88
- A. M. Hagighi, J. Medhi and S. G. Mohanty, “On a Multiserver Markovian Queuing System with Balking and Reneging,” Computer and Operational Research, Vol. 13, No. 4, 1986, pp. 421-425. http://dx.doi.org/10.1016/0305-0548(86)90029-8
- J. Bae, S. Kim and E. Y. Lee, “The Virtual Waiting time of the M/G/1 Queue with Impatient Customers,” Queuing Systems: Theory and Application, Vol. 38, No. 4, 2001, pp. 485-494.
- Y. Zhang, D. Yue and W. Yue, “Analysis of an M/M/1/N Queue with Balking, Reneging and Server Vacations,” International Symposium on OR and Its Applications. www.aporc.org/LNOR/6/ISORA2006F10.pdf
- M. S. El-Pauomy, “On Poisson Arrival Queue: MX/M/2/N with Balking, Reneging and Heterogeneous Servers,” Applied Mathematical Sciences, Vol. 2, No. 24, 2008, pp. 1169-1175.
- E. Altman and U. Yechiali, “Analysis of Customers’ Impatience in Queue with Server Vacations,” Queuing Systems, Vol. 52, No. 4, 2006, pp. 261-279. http://dx.doi.org/10.1007/s11134-006-6134-x
- E. Altman and U. Yechiali, “Infinite Server Queues with Systems Additional Tasks and Impatient Customers,” Probability in the Engineering and Information Sciences, Vol. 22, No. 4, 2008, pp. 477-493. http://dx.doi.org/10.1017/S0269964808000296
- R. Kumar and S. K. Sharma, “A Markovian Feedback Queue with Retention of Reneged Customers and Balking,” AMO-Advanced Modeling and Optimization, Vol. 14, No. 3, 2012, pp. 681-688.
- Y. Levy and U. Yechiali, “An M/M/s Queue with Server Vacations,” INFOR Journal, Vol. 14, No. 2, 1976, pp. 153-163.
- B. T. Doshi, “Queueing Systems with Vacations-A Survey,” Queueing Systems, Vol. 1, No. 1, 1986, pp. 29-66. http://dx.doi.org/10.1007/BF01149327
- J. Keilson and L. D. Servi, “The Dynamics of an M/G/1 Vacation Model,” Operations Research, Vol. 35, No. 4, 1987, pp. 575-582. http://dx.doi.org/10.1287/opre.35.4.575
- B. T. Doshi, “Analysis of a Two Phase Queueing System with General Service Times,” Operation Research Letters, Vol. 10, No. 5, 1991, pp. 265-275. http://dx.doi.org/10.1016/0167-6377(91)90012-E
- M. S. Kumar and R. Arumuganathan, “On the Single Server Batch Arrival Retrial Queue with General Vacation Time under Bernoulli Schedule and Two Phases of Heterogeneous Servers,” Quality Technology and Quantity Management, Vol. 5, No. 2, 2008, pp. 145-160.
- G. Choudhury, L. Tadj and M. Paul, “Steady State Analysis of an MX/G/1 Queue with Two Phase Service and Bernoulli Vacation Schedule under Multiple Vacation Policy,” Applied Mathematical Modelling, Vol. 31, No. 6, 2007, pp. 1079-1091. http://dx.doi.org/10.1016/j.apm.2006.03.032
- F. A. Maraghi, K. C. Madan and K. Darby-Dowman, “Bernoulli Schedule Vacation Queues with Batch Arrivals and Random System Breakdowns having General Repair Times Distribution,” International Journal of Operation Research, Vol. 7, No. 2, 2010, pp. 240-256.
- R. F. Khalaf, K. C. Madan and C. A. Lukas, “A MX/G/1 with Bernoulli Schedule General Vacation Times, General Extended Vacations, Random Breakdown, General Delay Time for Repairs to Start and General Repair Times,” Journal of Mathematical Research, Vol. 3, No. 4, 2011, pp. 8-20.
NOTES
*Corresponding author.

