American Journal of Operations Research
Vol. 2 No. 3 (2012) , Article ID: 22432 , 10 pages DOI:10.4236/ajor.2012.23044
Using Non-Additive Measure for Optimization-Based Nonlinear Classification
1College of Information Science and Technology, University of Nebraska at Omaha, Omaha, USA
2Nebraska Furniture Mart, Berkshire Hathaway Company, Omaha, USA
3Research Center on Fictitious Economy and Data Sciences, Chinese Academy of Sciences, Beijing, China
4Department of Mathematics, University of Nebraska at Omaha, Omaha, USA
5Guilin University of Electronic Technology, Guilin, China
Email: *yshi@unomaha.edu
Received May 22, 2012; revised June 20, 2012; accepted July 5, 2012
Keywords: Nonlinear Programming; Nonlinear Classification; Non-Additive Measure; Choquet Integral; Support Vector Machines
ABSTRACT
Over the past few decades, numerous optimization-based methods have been proposed for solving the classification problem in data mining. Classic optimization-based methods do not consider attribute interactions toward classification. Thus, a novel learning machine is needed to provide a better understanding on the nature of classification when the interaction among contributions from various attributes cannot be ignored. The interactions can be described by a non-additive measure while the Choquet integral can serve as the mathematical tool to aggregate the values of attributes and the corresponding values of a non-additive measure. As a main part of this research, a new nonlinear classification method with non-additive measures is proposed. Experimental results show that applying non-additive measures on the classic optimization-based models improves the classification robustness and accuracy compared with some popular classification methods. In addition, motivated by well-known Support Vector Machine approach, we transform the primal optimization-based nonlinear classification model with the signed non-additive measure into its dual form by applying Lagrangian optimization theory and Wolfes dual programming theory. As a result, 2n – 1 parameters of the signed non-additive measure can now be approximated with m (number of records) Lagrangian multipliers by applying necessary conditions of the primal classification problem to be optimal. This method of parameter approximation is a breakthrough for solving a non-additive measure practically when there are a relatively small number of training cases available (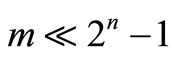 ). Furthermore, the kernel-based learning method engages the nonlinear classifiers to achieve better classification accuracy. The research produces practically deliverable nonlinear models with the non-additive measure for classification problem in data mining when interactions among attributes are considered.
). Furthermore, the kernel-based learning method engages the nonlinear classifiers to achieve better classification accuracy. The research produces practically deliverable nonlinear models with the non-additive measure for classification problem in data mining when interactions among attributes are considered.
1. Introduction
Classic optimization-based methods formulate classification problems by modeling data with standard optimization techniques using objectives and constraints. Mathematical programming provides general solution to the zoptimization problem. For example, references [1,2] proposed two classification models based on reducing the misclassification through minimizing overlaps or maximizing the distance of two data points in a linear system. A method named Multiple Criteria Linear Programming (MCLP) [3,4] has been initialized to compromise the objectives of models in [1] and [2] simultaneously and achieved a better data separation in a linear system. Alternatively, a quadratic model can be used to deal with linearly inseparable situation [5]. The key idea of those approaches is to separate data when they are in different classes as well as pull data together when they are in the same class. Initiated by [6], another well-known optimization-based classification method is Support Vector Machine (SVM), which mathematically constructs hyperplanes by support vectors. Further more, SVM separates data nonlinearly by introducing so-called nonlinear kernel functions.
Although these optimization-based methods separate data linearly or nonlinearly, they do not consider contributions from the interaction among attributes. In this paper, we use a nonadditive measure to model data with interactions and propose new nonlinear classification models. Nonlinear integrals can be used as tools to aggregate unknown parameters in the non-additive measure and values of attributes. As one of nonlinear integrals, the Choquet integral [7] is chosen as the aggregation tool for data modeling for classification problem. In addition, we investigate the direction of constructing nonlinear objectives by developing kernel functions in nonlinear classification models, a technique taken by SVM.
The rest of this paper is organized as follows: In Section 2, an overview of classic optimization-based classification methods is provided. Section 3 reviews definitions of non-additive measures and the Choquet integral. In Section 4, a new optimization-based classification model with a non-additive measure is proposed. Section 5 describes the Lagrangian optimization approach to solve the issue of dealing limited training samples with the proposed nonlinear classification model. Section 6 shows performance of the proposed models in experimental results. Finally, Section 7 provides conclusions from this research.
2. Preliminary
In this section, we provide an overview of classic optimization-based classification methods.
Consider that a dataset consists of n attributes and m records. Let X = {x1, x2, ···, xn} denote the set of feature attributes and y be the class label, where 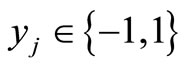 for a two classes dataset. The dataset has a form as follows:
for a two classes dataset. The dataset has a form as follows:

where following elements

are the values of attributes x1, x2, ···, xn for the j-th record in the dataset, denoted by fj, j = 1, ···, 2, m. Note that fj can be regarded as a vector. In addition, yj is the corresponding class label in the j-th record.
The mathematical programming or optimization-based approach have been widely used for many applications. Particularly, numerous mathematical programming methods based on optimization techniques have been proposed for solving classification problem [1-3,6]. In classification, the concept of classes is generally expressed as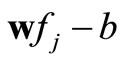 , where w, fj, and b represent attribute weights, values, and classification critical value respectively. Therefore, wfj is the weighted sum of all the attributes. For a dataset with two classes, the decision function for the classes are defined as:
, where w, fj, and b represent attribute weights, values, and classification critical value respectively. Therefore, wfj is the weighted sum of all the attributes. For a dataset with two classes, the decision function for the classes are defined as:
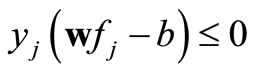
where yj = 1 if the j-th record belongs to class 1 and yj = –1 if the j-th record belongs to class 2.
The two linear classification methods [1,2] based on the idea of reducing misclassification by minimizing the overlaps or maximizing the sum of distances in a linear system. One approach is to maximize the sum of minimum distances (MMD) of data from the critical value. Another approach separates the data by minimizing the sum of deviations (the overlapped distances between classes) (MSD) of data from the critical value. These two classic linear classification models can easily be described with a standard form of optimization, i.e.
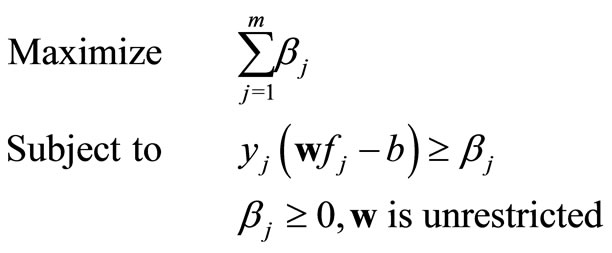 (MMD)
(MMD)
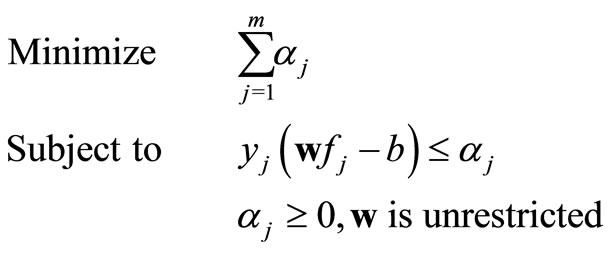 (MSD)
(MSD)
where αj denotes the degree of the overlapping of the two classes and βj denotes the distances from the observation to the critical classification value b. The weights w are optimized by linear programming, a typical optimization technique. The critical value b is given as a constant non-zero real number.
The above two linear classification models provide the basic idea of data separation, which pulls the data apart from the boundary (maximize the sum of βj in MMD) or to make the smallest data overlapping area (minimize the sum of αj in MSD). However there are some optimization difficulties in those approaches. For example, the MMD model cannot be optimized because the value of βj can reach as large as possible since the goal is to maximize the sum of βj. Thus, in the implementation of MMD model, βj is bounded as βj ≤ β*, where β* is a given positive constant. The MMD classification model is only able to classify linearly separable dataset. Similarly, the αj in MSD model has to be bounded to a very small positive value α* as αj ≥ α*.
Efforts have been made to improve optimization-based linear classification for better dealing with linearly inseparable. For example, MCLP approach was initiated by compromising two objectives of MMD and MSD simultaneously and achieved a better classification within a linear system [3]. MCLP model compromises objectives as [3]:
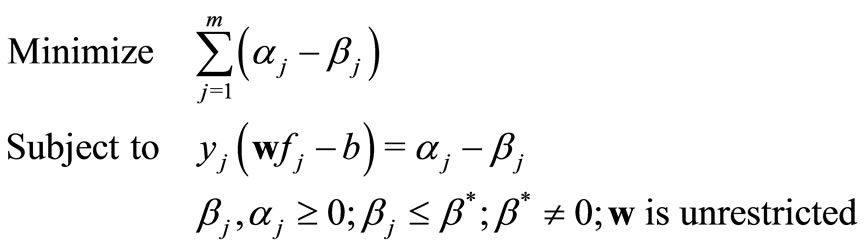 (MCLP)
(MCLP)
where β* is a positive constant to restrict the upper bound of βi.
Another direction of improving optimization-based classification is to develop nonlinear models by constructing nonlinear objectives, such as the Multiple Criteria Quadratic Programming (MCQP), a nonlinear optimization classification [5].
3. Non-Additive Measures
A common characteristic of the methods described above is that the modeling is based on the assumption that contributions from all attributes toward classification are the sum of contributions of each attribute. None of those methods considers the interactions among attributes toward classification, which may provide a better understanding of the nature of classification and achieve more satisfactory results. In addition, the model should be able to represent the underlying phenomenon of applications such as classification in a more adequate manner because attributes are not completely isolated from each other. Such a model should have the potential of increased robustness, defined as the ability of maintaining effective performance on both training and testing results on a diversity of datasets. Particularly, a classification model is said to be robust when the performance of its testing results is not significantly distant from training.
The theory of non-additive measure can achieve increased robustness and better performance in classification. The bases of non-additive measures and the nonlinear integrals are briefly reviewed in the rest of this section.
3.1. Definition of Non-Additive Measures
The attribute interactions can be represented by a non-additive measure. The concept of non-additive measure (also referred to as fuzzy measure theory) was initiated in the 1950s and has been well developed since 1970s [7-9].
Let finite set X = {x1, ···, xn} denote the attributes in a multidimensional dataset. Several important types of non-additive measure are defined as the followings [8]:
Definition 1. A non-additive measure μ defined on X is a set function 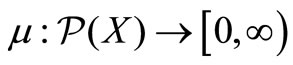 satisfying
satisfying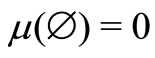 , where
, where 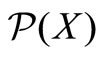 denotes the power set of X, μ is monotone if it satisfies
denotes the power set of X, μ is monotone if it satisfies 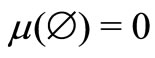 and
and 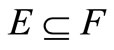 if
if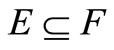 , where E, F are any sets in
, where E, F are any sets in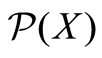 .
.
Definition 2. A signed non-additive measure μ is defined on X is a set function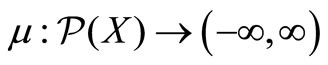 .
.
The values of non-additive measure μ are unknown parameters. The signed non-additive measure is adopted to develop optimization-based nonlinear classification models.
3.2. Choquet Integral
Nonlinear integrals are used as data aggregation tools to integrate the values of attributes with respect to a nonadditive measure. As one of nonlinear integrals, the Choquet integral is more appropriate for applications such as classification because it provides very important information in interactions among attributes [10].
Now let the values of 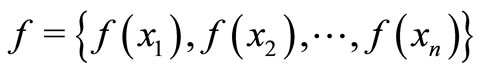 denote the values of each attribute in the dataset; let
denote the values of each attribute in the dataset; let  be the non-additive measure. The general definition of the Choquet integral, with function
be the non-additive measure. The general definition of the Choquet integral, with function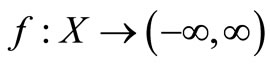 , based on signed non-additive measure μ, is defined in formula 1 as
, based on signed non-additive measure μ, is defined in formula 1 as
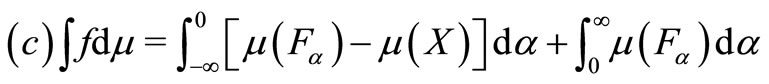 (1)
(1)
where 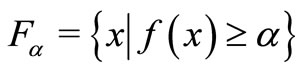 is called α-cut set of f, for
is called α-cut set of f, for , n is the number of attributes in the dataset.
, n is the number of attributes in the dataset.
Choquet integral may be calculated as [11]:
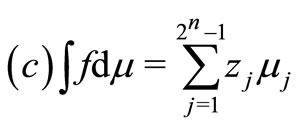 (2)
(2)
where
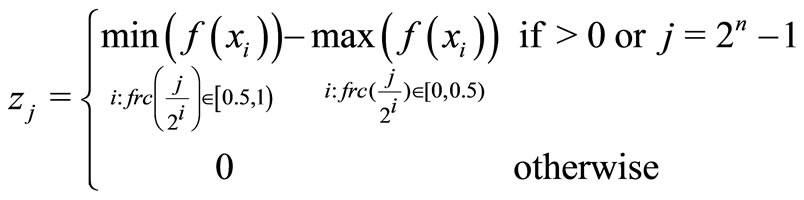 (3)
(3)
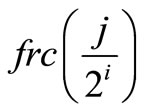
is the fractional part of 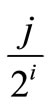
and the maximum operation on the empty set is zero. Let jn, jn – 1, ···, j1 represent the binary form of j, the i in formula 3 is determined as following:
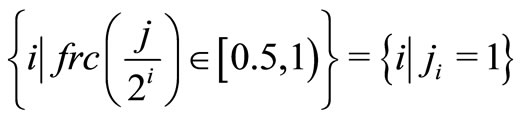
and
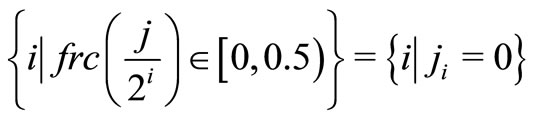
It is important to emphasize that the concept of Choquet integral is not equal to a nonadditive measure μ. Rather, it is a mathematical tool aggregating the values of attributes with respect to the signed non-additive measure μ; as such, it is similar to the linear weighted sum to aggregate the corresponding attribute with respect to the weights in a linear model such as MSD.
4. Optimization-Based Nonlinear Classifiers with Non-Additive Measures
The idea of using non-additive measure in classification problem is not new. In the fuzzy measure community, non-additive measures have been utilized for modeling attribute interactions for data separation purpose. For example, reference [12] used the Choquet integral with respect to the non-additive measure on statistical pattern classification based on possibility theory, an optimization-based classification model was later proposed with a non-additive measure [13]. Reference [14] proposed the k-Interactive (k = 2) classification with feature selections based on a pattern matching algorithm similar to [12]. Classification can also be achieved by directly separating the date using the weighted Choquet integral projection [15] or using a penalized signed fuzzy measure [16]. A detailed discussion of geometric meaning of the contributions from feature attributes in nonlinear classification can be found in [17].
There are limitations on above methods, notably: (a) Impractical: Due to the complexity of the non-additive measure, the methods were only applicable for datasets with small number of attributes, generally less than 5. (b) Limited performance: the classification accuracy was not promising compared to other popular methods [13] due to lack of better learning algorithms for determining unknown parameters of a non-additive measure. For instance, classification model in [15] with the Choquet integral has infinite number of solutions and the proposed method can only determine one of them. To address these limitations, this current research intends to provide a more practical and powerful solution toward nonlinear classification with a non-additive measure.
In addition, early studies of non-additive measure for classification also show limitations on classification accuracy and scalability. For example, although classification model in [12] is well developed in theory (similar to Bayesian classifier), the classification did not show any benefits of using non-additive measure and it is even more difficult to obtain good results on small Iris dataset, a benchmark dataset from UCI Machine Learning Repository (http://archive.ics.uci.edu/ml/). An optimizationbased nonlinear classification model [13] with a nonadditive measure was later proposed and studied. The results show it even performs worse than linear classifier on iris dataset and only competitive to fuzzy k-NN classifier on other datasets. The research [13] suggests a better non-additive identification algorithm is needed.
An improvement for nonlinear optimization-based classifiers with non-additive measure might be the optimization process of the critical value for classification. Inn MCLP model, the classification critical value b is not optimized but arbitrarily chosen. A better method to determine b could be updating b with the average of the lowest and largest predicted scores [15] during learning iterations. Alternatively, the critical value b in MCLP also can be replaced with soft-margin b ± 1 similar to SVM which constructs a separation belt instead of a single cutting line. With this technique, it is guaranteed to produce a unique solution to the model because the goal of the optimization is to find the cutting line which is most close to the misclassified data points on both sides. The MCLP model can be extended to a linear programming solvable problem with optimized b and the signed non-additive measure, as shown below:
 (M1)
(M1)
where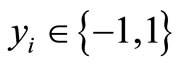 , μ, b and α are critical values to be determined. Model M1 can be solved by standard linear programming techniques such as the simplex method. However, the number of μ, which is 2n – 1, is exponentially related to the number of attributes (n) because of power set operation in the Choquet integral. When the number of records (m) in the training set is relatively small (e.g.
, μ, b and α are critical values to be determined. Model M1 can be solved by standard linear programming techniques such as the simplex method. However, the number of μ, which is 2n – 1, is exponentially related to the number of attributes (n) because of power set operation in the Choquet integral. When the number of records (m) in the training set is relatively small (e.g. ), the model is difficult to be solved. In the next section, we propose a compromised solution to deal with this situation.
), the model is difficult to be solved. In the next section, we propose a compromised solution to deal with this situation.
5. Nonlinear Classification with the Signed Non-Additive Measure by Lagrangian Optimization
As mentioned, it is hard to optimize the non-additive optimization-based classification models when there are not enough observations (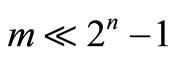 ). The existing approaches such as hierarchical Choquet integral [18] and the k-Interactive measure [14] ignored some values of non-additive measure μ to some extent. As a solution, the Lagrangian optimization theory can be incorporated to transform the model into practically solvable form with the best approximation of parameters of non-additive measure μ. The Karush-Kuhn-Tucker (KKT) conditions [19] applied in the Lagrangian optimization process are the necessary conditions to guarantee an optimizationbased classification model to reach optimum. To develop a nonlinear classifier which can deal with this situation, a quadratic non-additive optimization-based model is constructed and transformed.
). The existing approaches such as hierarchical Choquet integral [18] and the k-Interactive measure [14] ignored some values of non-additive measure μ to some extent. As a solution, the Lagrangian optimization theory can be incorporated to transform the model into practically solvable form with the best approximation of parameters of non-additive measure μ. The Karush-Kuhn-Tucker (KKT) conditions [19] applied in the Lagrangian optimization process are the necessary conditions to guarantee an optimizationbased classification model to reach optimum. To develop a nonlinear classifier which can deal with this situation, a quadratic non-additive optimization-based model is constructed and transformed.
5.1. Lagrangian Theory for Optimization
The Lagrangian theory is intended to provide the necessary conditions for a given nonlinear optimization problem to reach an optimal solution. The KKT conditions in the Lagrangian optimization provide the necessary conditions for the proposed classification model to have an optimal solution. Generally, an optimization problem can be presented as [20]:
Definition 3. Given functions f, gi, i = 1, ···, k, and hi, i = 1, ···, m, defined on vector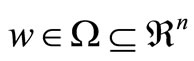 , the primal optimization problem is defined as:
, the primal optimization problem is defined as:
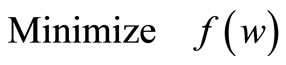
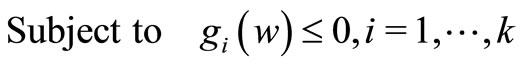
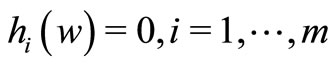
The generalized Lagrangian function corresponding to the definition 3 is
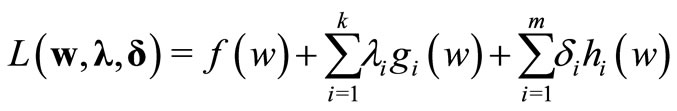
where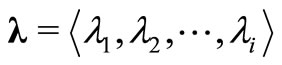 ,
, 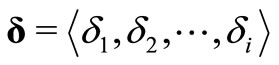 are the Lagrangian multipliers and
are the Lagrangian multipliers and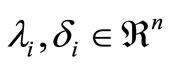 .
.
Instead of solving the primal optimization problem, an alternative is to optimize the Lagrangian dual problem, which is defined as
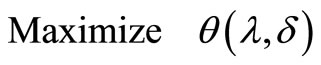 ,
,

where , the greatest lower bound on Lagrangian function L over Ω. The optimal solution for the objective function is called the value of the problem.
, the greatest lower bound on Lagrangian function L over Ω. The optimal solution for the objective function is called the value of the problem.
The following Karush-Kuhn-Tucker theorem Tucker 1951 gives the necessary conditions for an optimal solution to general optimization problem.
Theorem 1. Given an optimization problem as defined in definition 3, the necessary and sufficient conditions for a point w* to be an optimum are, 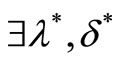 , such that
, such that
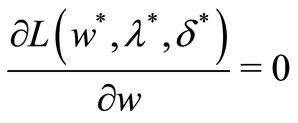
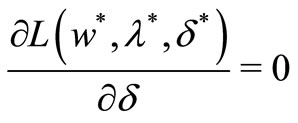
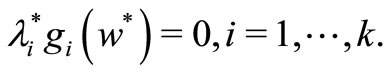
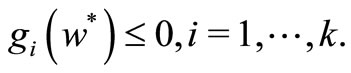
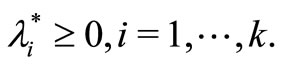
The first two conditions are also the necessary conditions for the optimization problem to reach optimal. The third condition is called KKT complementary condition. The first two conditions are also the necessary conditions for the optimization problem to reach optimal. The sufficient condition is true only if function (L) of w is convex. In this research, since the convexity of the primal problem is yet to be proved, only the necessary conditions can be considered. Since the constraints of the primal optimization problem does not have the condition of equality, only the first two conditions and 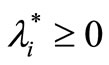 are to be applied. Thus, the lagrangian function for this particular optimization problem is described as:
are to be applied. Thus, the lagrangian function for this particular optimization problem is described as:
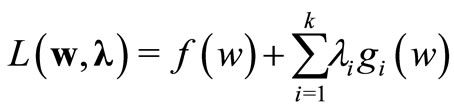
A necessary condition for a normal point w* to be a minimum of f(w) subject to gi(w) = 0, i = 1, ···, k, is Cristianini2000:
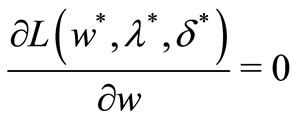
for some values of λ*.
5.2. Quadratic Non-Additive Optimization-Based Classification
We extend model M1 to a quadratic programming form and rewrite to model M2, as follows:
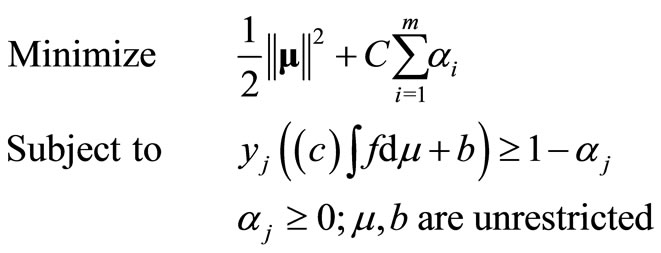 (M2)
(M2)
where 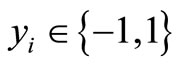
It is important to note that 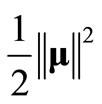 is a constructed objective for modeling purpose. The constant C is normally set to be very large to minimize the impact from the constructed objective.
is a constructed objective for modeling purpose. The constant C is normally set to be very large to minimize the impact from the constructed objective.
5.3. Nonlinear Classifier with the Non-Additive Measure
The optimization problem M2 can be transformed into its corresponding dual problem. Similar to the optimization process of Support Vector Machine Cristianini2000, firstly, the primal Lagrangian is:
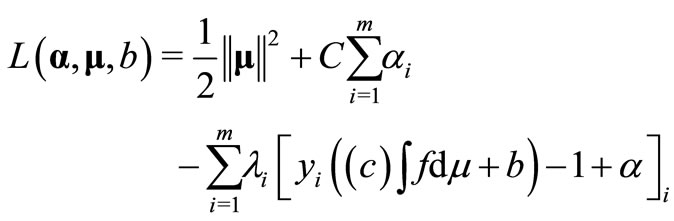
where λi are the Lagrangian multipliers and C is a given relatively large positive constant. According to the general definition of the Choquet integral:

Define vectors zi, α, λ, μ as
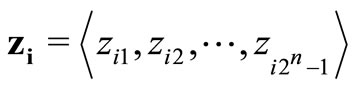
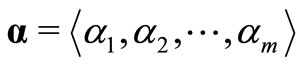
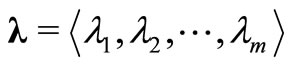
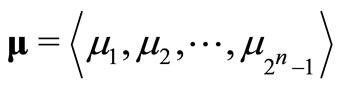
Thus,

Now the necessary KKT conditions are applied on the primal Lagrangian function L by taking the partial derivative of L with respect to μ, α and b to be zero as follows:

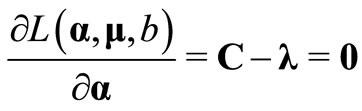
where C is a constant vector and is defined as:
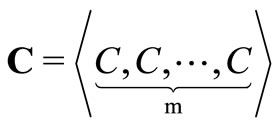
Therefore, the following conditions hold:
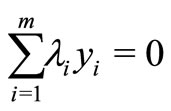
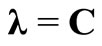
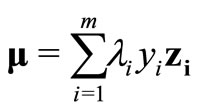
Thus, after applying the necessary conditions on L, the primal becomes
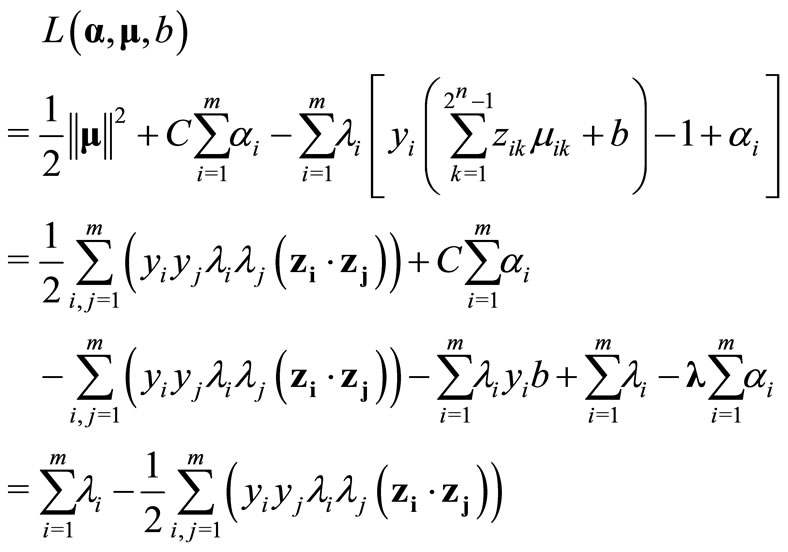
where 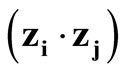 denotes the inner product of zi and zj.
denotes the inner product of zi and zj.
The primal problem can be transformed into its dual problem according to Wolfe’s dual programming theory, as the following shows:
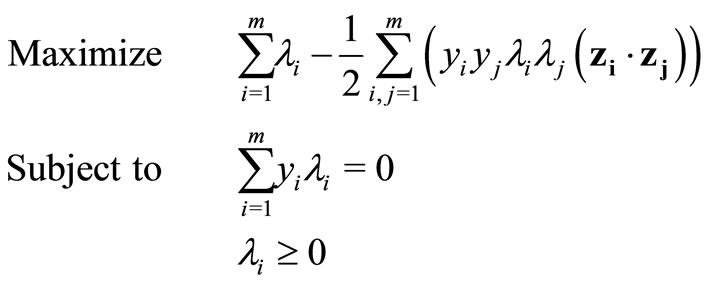
where .
.
Since λ = C and elements in C are constants, and the model can be further simplified as:
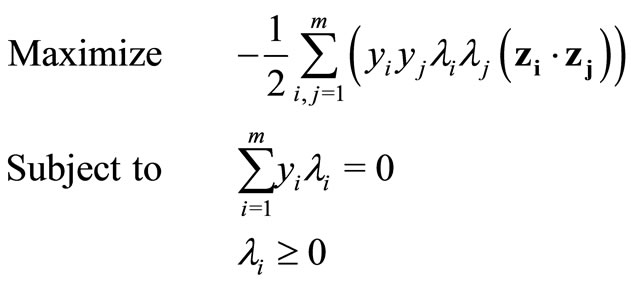
where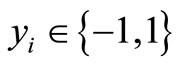 .
.
Model M3 can be regarded as a general optimizationbased nonlinear classifier with the signed non-additive measure. In addition, the inner product can be further replaced with kernel functions to deliver more accurate classification.
It is observed that for constructing optimal separation in a feature space, one does not need to consider the feature space in explicit form, but only has to calculate the inner products between support vectors and the vectors of the future space [21]. Thus, the inner product operation can be replaced with kernel functions K, the function that corresponds to an inner product in the expanded feature space. Nonlinear kernel functions are able to map the data into hyper space to achieve better classification.
The three well-known kernel functions have been adopted by Model M3. They are linear, Polynomial and RBF kernel functions.
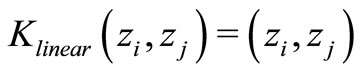 (innerproduct/linear Kernel)
(innerproduct/linear Kernel)
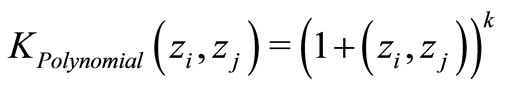 (Polynomial Kernel)
(Polynomial Kernel)
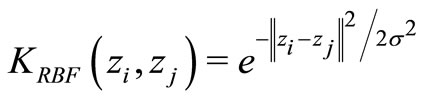 (RBF Kernel)
(RBF Kernel)
By solving M3 with standard optimization technique, the number of parameters to be optimized is reduced from level of 2n to m.
Model M3 with kernel functions can be solved by Sequential Minimal Optimization (SMO) [22]. SMO algorithm decomposes the original QP (Quadratic Programming) problem into smaller QP problem by heuristically choosing two Language multipliers, which makes the smallest possible optimization problem. For each small QP problem, an analytic method is used for solving the two Language multipliers. Through altering two Language multipliers at each step, the objective function will be decreased and the convergence is guaranteed according to Osuna’s theorem Osuna [23].
In conclusion, we point out that the applied KKT conditions are the necessary conditions for the classification model to reach optimum. Model M2 is transformed into its dual form M3 during the Lagrangian optimization to deal with the case of learning with small training dataset (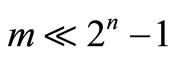 ). Through this compromised solution, the 2n – 1 parameters of the signed non-additive measure can now be approximated by m Lagrangian multipliers.
). Through this compromised solution, the 2n – 1 parameters of the signed non-additive measure can now be approximated by m Lagrangian multipliers.
6. Applications
The proposed Model M3 has been applied on both artificial and UCI machine learning datasets for classification purpose and compared with performance of other methods.
There are two artificial datasets with two classes randomly generated according to the definition of the Chouqet integral. One dataset has two dimensions (2D) and the other has three (3D). The 5-fold cross-validation is used for classification evaluation. Model M3 is also compared to other popular classification methods, such as SVMs, Decision Tree (J48), Logistic Regression and Naive Bayes. The average classification accuracy in percentage is summarized in Table 1 for evaluating testing sets in all 5 folders. As a result, M3 performs best on both artificial datasets when nonlinear kernel methods are used although performance of different kernel methods varies. The results confirm the theoretical assumption that models with non-additive measure can deal with attribute interactions because the datasets were created based on features of the Choquet integral.
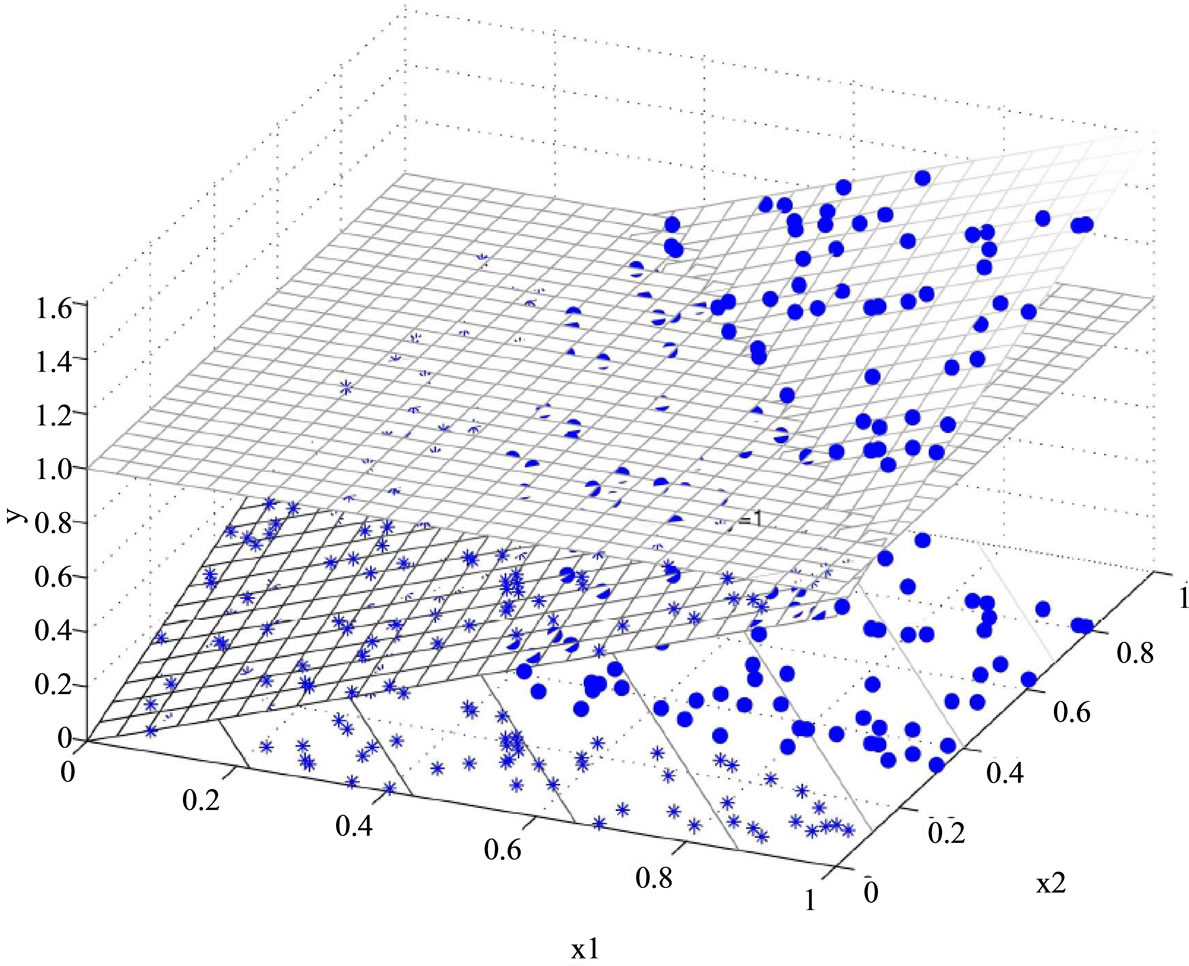
To better understand this nonlinear classification, we visually represent how Model M2 (the primal problem) to perfectly classify the two dimensional artificial dataset in Figure 1. The example was taken from fold-1 training set of the two dimensional artificial dataset. This training set contains 160 data points, including 85 in class 1 and 75 in class 2. Model M2 creates a three dimensional decision space (x1, x2, y), where x1, x2 are the attributes of the two dimensional dataset and y is the decision score of M2. The model classifies data as class 1 when y > b, otherwise class 2. Figure 1 presents one solution from the cross validation. In Figure 1(a) data points belonging to
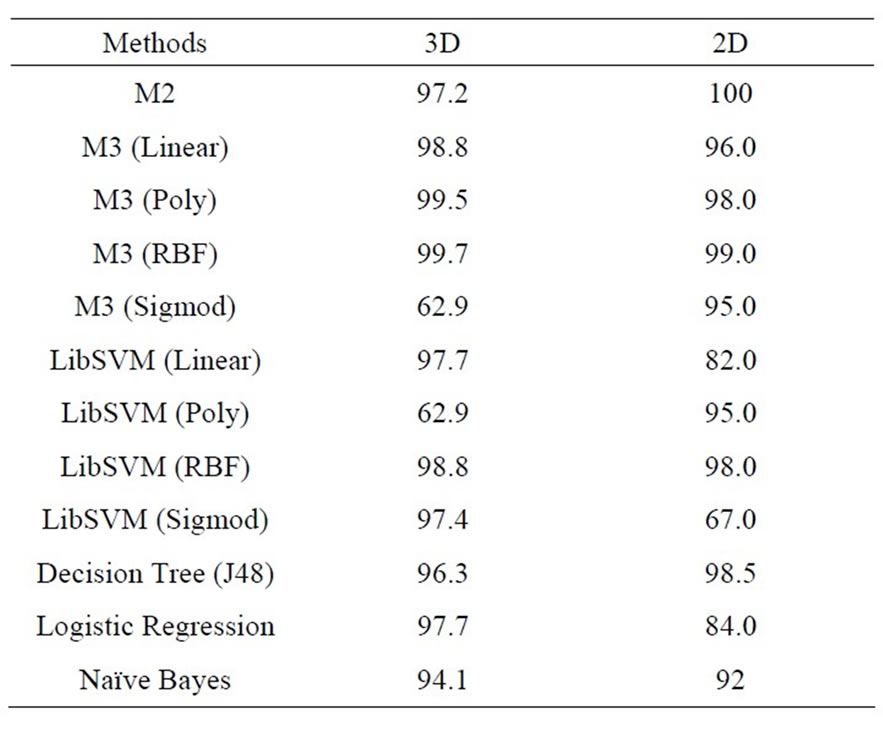
Table 1. Classification accuracy on two artificial datasets.
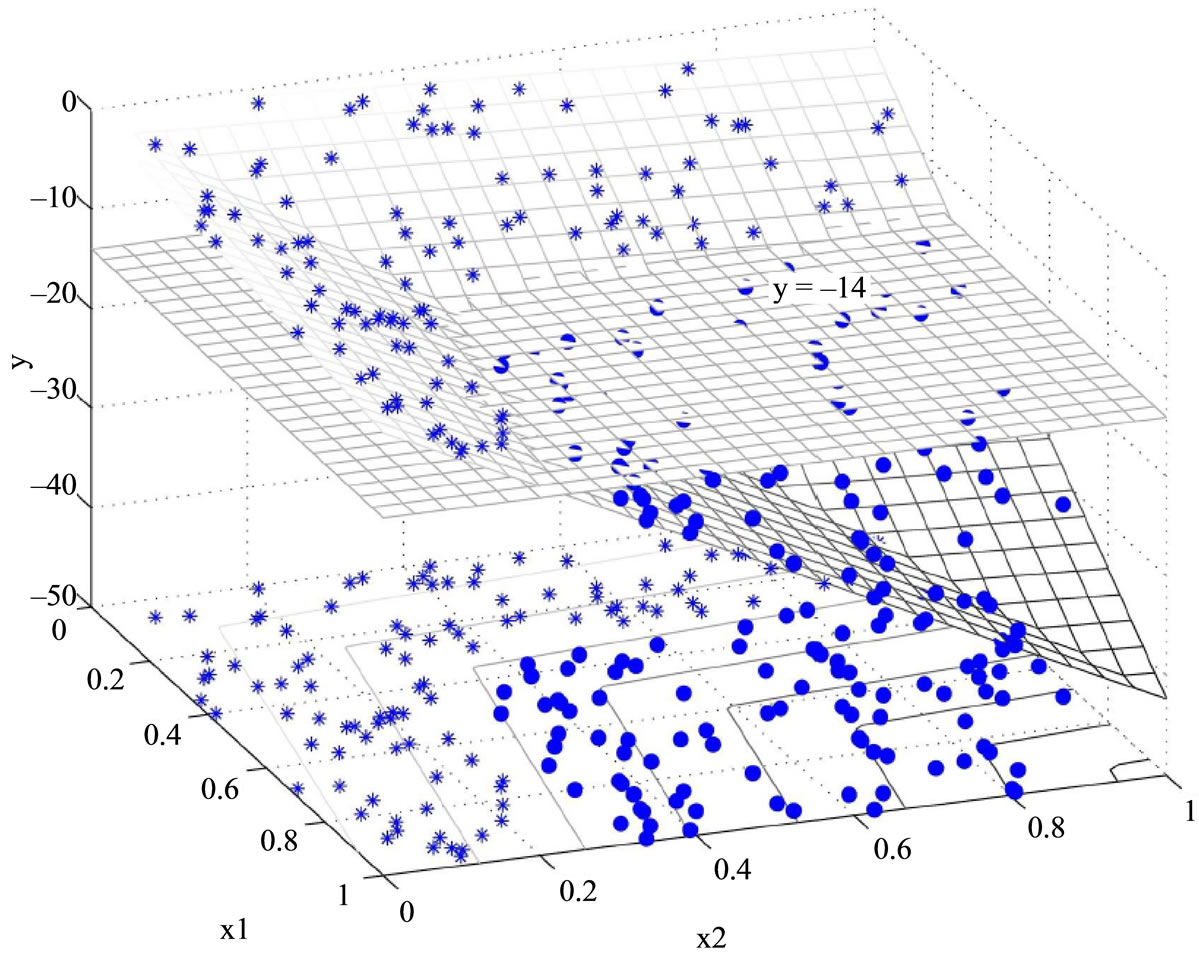 (a)
(a)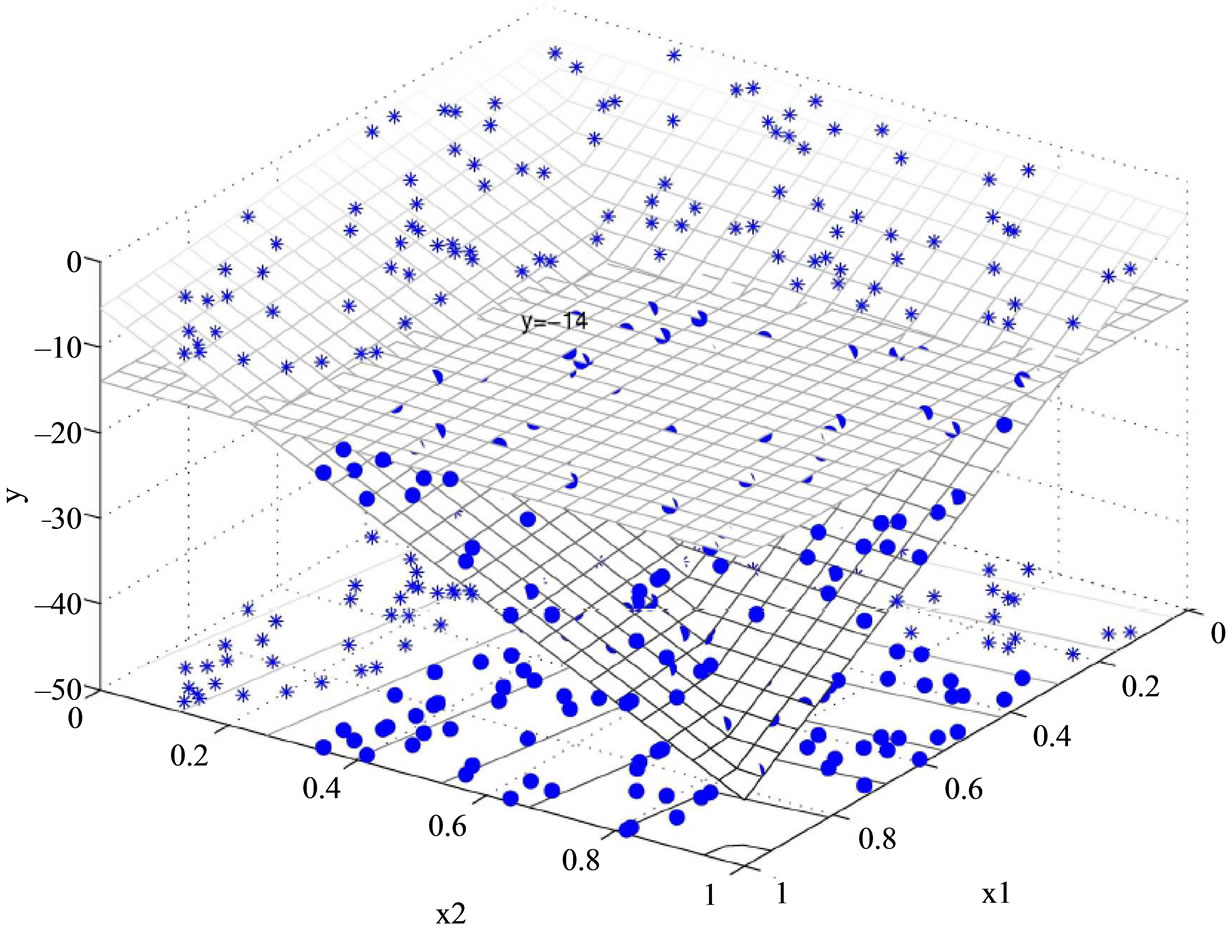 (b)
(b)
Figure 1. Nonlinear classification by Model M2. (a) View 1; (b) View 2.
two classes are represented by asterisks (.) and dots (.), respectively. The data points shown on the bottom of the figure depict the original 2D data, which are apparently not linearly separable. After applying Choquet integral to create a third dimension y, the corresponding 3D data points are now located in two different 2D planes, and are now linearly separable. Figure 1(b) represents the same data set but provides a different perspective to view the data. The linearly inseparable two dimensional dataset x1, x2 is lifted into a hyper space (x1, x2, y) by M2 and then can be easily classified by the decision boundary y = –14 (value of the critical value b).
In addition, the data cannot be perfectly classified by the linear model MSD as Figure 2 shows. After applying MSD model, the corresponding 3D data points are still located in one flat surface in the three dimensional space and the two classes cannot be linearly separated. In MSD model, the critical value b is set to 1 and the MSD classification model separates data by decision function y = w1f1 + w2f2 (y > 1 indicates class 1 and y < 1 for class 2), with the solution w1 = 0.92, w2 = 0.70.
Classification of UCI Datasets
The UCI’s Pima Indian Diabetes and the Australian Credit Approval datasets were classified with model M3. The Australian dataset contains two classes (approval or not) and it has 14 attributes and 690 instances. Both datasets were transformed into [–1, 1] with z-score normalization and the 5-folder cross-evaluation was conducted for the application. The constant variable c was set to 100000 for all the experiments. Table 2 is the summarization of the results compared with the SVM classifier with RBF kernel.
The above results show that M3 outperformed SVM with RBF kernel on the Australian credit dataset which indicates the model is more robust when the dataset has more feature attributes, in the sense of that the performance of the testing is not significantly worse then the training. Our experiences also show that the use of Lagrangian optimization makes it feasible to solve nonadditive measure when the number of attributes is up to 14. The use of kernel functions also ensured the classification accuracy of the nonlinear model with the signed non-additive measure.
7. Conclusion
We have proposed a new classification approach based on optimization-based models while the attributes interactions are considered. The theory of non-additive measures were utilized to model the data with interactions.
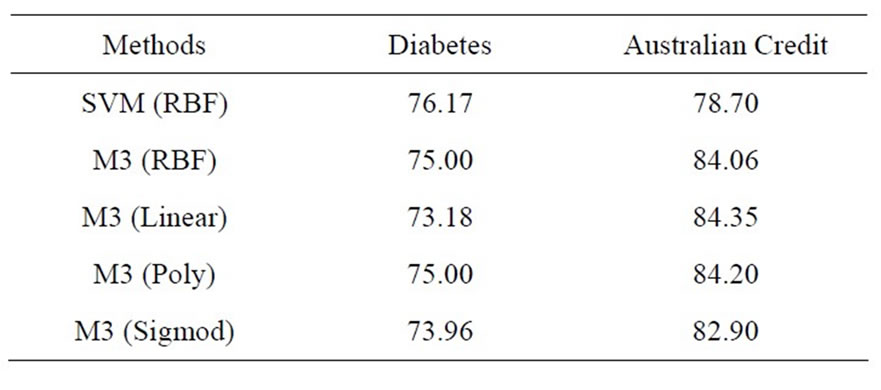
Table 2. Classification results on two UCI datasets.
 (a)
(a)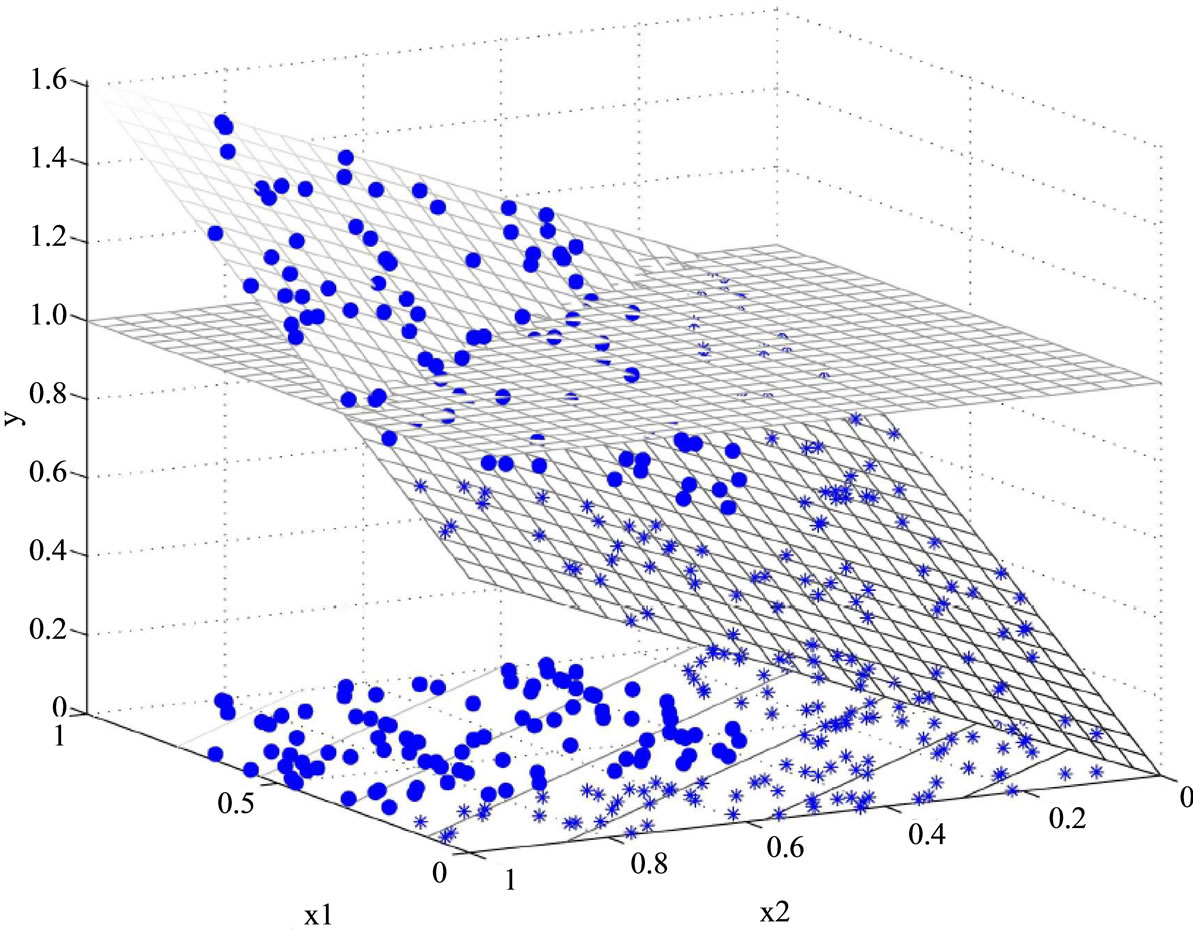 (b)
(b)
Figure 2. Linear classification by Model MSD. (a) View 1; (b) View 2.
Traditionally, nonlinear integrals are the aggregation tools for non-additive measures. The Choquet integral is good for data modeling purpose. We have demonstrated the value of using non-additive measure on optimizationbased classification and proposed a more efficient nonlinear model M3, which can classify data by solving less number of parameters. The 2n – 1 parameters of the signed non-additive measure can now be approximated by m Lagrangian multipliers. The optimization of the dual model M3 is guaranteed by KKT conditions, which are the necessary conditions for the nonlinear programming to be optimal. This method of parameter approximation is useful when the training set has limited number of samples. The proposed approach is thus suitable for classification applications where training sample is small comparing with the number of attributes. The experiment on the artificial dataset demonstrated the geometric meaning and profound theory of the nonlinear classification models. Applications on UCI datasets have shown that this nonlinear approach increases model robustness as the classification accuracy is stable and the accuracy of testing results is close to that of the training results. We are now in the process of applying our approach to various data mining applications.
8. Acknowledgements
This work has been partially supported by grants from Nebraska EPSCoR Program, USA, Nebraska Furniture Market Co., USA, BHP Billiton Co, Australia, Innovative Group from National Natural Science Foundation of China (#70921061, #70621001, #70901011), China and the CAS/SAFEA International Partnership Program for Creative Research Teams, China.
REFERENCES
- N. Freed and F. Glover, “Simple but Powerful Goal Programming Models for Discriminate Problems,” European Journal of Operational Research, Vol. 7, No. 1, 1981, pp. 44-60. doi:10.1016/0377-2217(81)90048-5
- N. Freed and F. Glover, “Evaluating Alternative Linear, Programming Models to Solve the Two-Group Discriminate Problem,” Decision Science, Vol. 17, No. 2, 1986, pp. 151-162. doi:10.1111/j.1540-5915.1986.tb00218.x
- Y. Shi, “Multiple Criteria and Multiple Constraint Levels Linear Programming: Concepts, Techniques and Applications,” World Scientific Pub Co Inc., New Jersey, 2001.
- G. Kou, Y. Peng, Z. Chen and Y. Shi, “Multiple Criteria Mathematical Programming for Multi-Class Classification and Application in Network Intrusion Detection,” Information Sciences, Vol. 179, No. 4, 2009, pp. 371-381. doi:10.1016/j.ins.2008.10.025
- Y. Peng, G. Kou, Y. Shi and Z. Chen, “A Multi-Criteria Convex Quadratic Programming Model for Credit Data Analysis,” Decision Support Systems, Vol. 44, No. 4, 2008, pp. 1016-1030. doi:10.1016/j.dss.2007.12.001
- V. Vapnik, “The Nature of Statistical Learning Theory,” Springer-Verlag, New York, 1995.
- G. Choquet, “Theory of Capacities,” Annales de l’Institut Fourier, Vol. 5, 1954, pp. 131-295. doi:10.5802/aif.53
- Z. Wang and G. J. Klir, “Fuzzy Measure Theory,” Plenum, New York, 1992.
- Z. Wang and G. J. Klir, “Generalized Measure Theory,” Springer, New York, 2008.
- Z. Wang, K.-S. Leung and G. J. Klir, “Applying Fuzzy Measures and Nonlinear Integrals in Data Mining,” Fuzzy Sets and Systems, Vol. 156, No. 3, 2005, pp. 371-380. doi:10.1016/j.fss.2005.05.034
- Z. Wang and H. Guo, “A New Genetic Algorithm for Nonlinear Multiregressions Based on Generalized Choquet Integrals,” The 12th IEEE International Conference on Fuzzy Systems (FUZZ’03), Vol. 2, 25-28 May 2003, pp. 819-821.
- M. Grabisch and M. Sugeno, “Multi-Attribute Classification Using Fuzzy Integral,” IEEE International Conference on Fuzzy System, San Diego, 8-12 March 1992, pp. 47-54.
- M. Grabisch and J.-M. Nicolas, “Classification by Fuzzy Integral: Performance and Tests,” Fuzzy Sets System, Vol. 65, No. 2-3, 1994, pp. 255-271. doi:10.1016/0165-0114(94)90023-X
- L. Mikenina and H. J. Zimmermann, “Improved Feature Selection and Classification by the 2-Additive Fuzzy Measure,” Fuzzy Sets and Systems, Vol. 107, No. 2, 1999, pp. 197-218. doi:10.1016/S0165-0114(98)00429-1
- K. Xu, W. Z., P. Heng and K. Leung, “Classification by Nonlinear Integral Projections,” IEEE Transactions on Fuzzy Systems, Vol. 11, No. 2, 2003, pp. 187-201. doi:10.1109/TFUZZ.2003.809891
- H. Fang, M. Rizzo, H. Wang, K. Espy and Z. Wang, “A New Nonlinear Classifier with a Penalized Signed Fuzzy Measure Using Effective Genetic Algorithm,” Pattern Recognition, Vol. 43, No. 4, 2010, pp. 1393-1401. doi:10.1016/j.patcog.2009.10.006
- J. Chu, Z. Wang and Y. Shi, “Analysis to the Contributions from Feature Attributes in Nonlinear Classification Based on the Choquet Integral,” 2010 IEEE International Conference on Granular Computing (GrC), San Jose, 14-16 August 2010, pp. 677-682.
- T. Murofushi, M. Sugeno and K. Fujimoto, “Separated Hierarchical Decomposition of the Choquet Integral,” International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, Vol. 5, No. 5, 1997, pp. 563-585. doi:10.1142/S0218488597000439
- H. Kuhn and A. Tucker, “Nonlinear Programming,” Proceedings of 2nd Berkeley Symposium on Mathematical Statistics and Probabilistics, 1951, pp. 481-491.
- N. Cristianini and J. Shawe-Taylor, “An Introduction to Support Vector Machines,” Cambridge University Press, Cambridge, 2000.
- B. Boser, I. Guyon and V. N. Vapnik, “A Training Algorithm for Optimal Margin Classifiers,” 5th Annual Workshop on Computational Learning Theory, 1992, pp. 144- 152. doi:10.1145/130385.130401
- J. Platt, “Fast Training of Support Vector Machines Using Sequential Minimal Optimization,” Technical Report, Microsoft Research, 1998.
- E. Osuna, R. Freund and F. Girosi, “An Improved Training Algorithm for Support Vector Machines,” Neural Networks for Signal Processing [1997] VII. Proceedings of the 1997 IEEE Workshop, Amelia Island, 24-26 September 1997, pp. 276-285.
NOTES
*Corresponding author.

