American Journal of Operations Research
Vol. 2 No. 1 (2012) , Article ID: 17835 , 6 pages DOI:10.4236/ajor.2012.21012
Allocation in Multivariate Stratified Surveys with Non-Linear Random Cost Function
1CSIRO Department of Mathematics, Integral University, Lucknow, India
2Department of Statistics & Operations Research, Aligarh Muslim University, Aligarh, India
Email: *irfii.ali@gmail.com
Received December 25, 2011; revised January 26, 2012; accepted February 12, 2012
Keywords: Stratified Survey; Optimum Allocation; Compromise Allocation; Stochastic Programming; Chance Constraints; Modified E-Model
ABSTRACT
In this paper, we consider an allocation problem in multivariate surveys with non-linear costs of enumeration as a problem of non-linear stochastic programming with multiple objective functions. The solution is obtained through Chance Constrained programming. A different formulation of the problem is also presented in which the non-linear cost function is minimised under the precision constraints on estimates of various characters. The solution is then obtained by using Modified E-model. A numerical example is solved for both the formulations.
1. Introduction
In multivariate stratified sampling where more than one characteristic are to be estimated, an allocation which is optimum for one characteristic may not be optimum for other characteristics. In such situations a compromise criterion is needed to work out a usable allocation which is optimum for all characteristics in some sense. Such an allocation may be called a “Compromise Allocation”.
Several authors have studied various criteria for obtaining a usable compromise allocation. Among them are Neyman [1], Dalenius [2], Gosh [3], Yates [4], Aoyama [5], Folks and Antle [6], Kokan and Khan [7], Chatterji [8], Ahsan and Khan [9], Jahan et al. [10], Khan et al. [11] and many others.
The problem of optimum allocation in stratified sampling is generally stated in two ways. Either one minimizes the cost of survey for a desired precision or the variance of the sample estimate is minimized for a given budget of the survey. Kokan and Khan [7] formulated the minimization of the cost of the survey for desired precisions on various characters as the following convex programming problem;
 (1.1)
(1.1)
where L is the number of strata,  is the number of characters to be estimated in the survey and
is the number of characters to be estimated in the survey and 
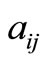 ,
, 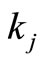 and
and  are all positive constants.
are all positive constants.
If the budget of the survey is fixed in advance, say, 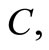 then the multivariate allocation problem is stated to minimize the variances for various characters for a desired precision as the following
then the multivariate allocation problem is stated to minimize the variances for various characters for a desired precision as the following  convex programming problems;
convex programming problems;
 (1.2)
(1.2)
Further, in a survey the costs for enumerating a character in various strata are not known exactly, rather these are being estimated from sample costs. As such the formulated allocation problem should be considered as stochastic programming problem. When the constants  and
and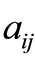 ,
, 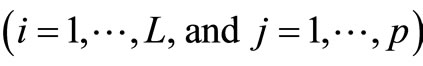 are fixed, the problem (1.1) was solved by Kokan and Khan by using an analytical procedure. Prekopa [12] developed a method from stochastic point of view. The case when sampling variances are random in the constraints (i.e.
are fixed, the problem (1.1) was solved by Kokan and Khan by using an analytical procedure. Prekopa [12] developed a method from stochastic point of view. The case when sampling variances are random in the constraints (i.e. 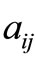 random in (1.1)) has been dealt with Diaz-Garcia and Garay Tapia [13]. Javed et al. [14] considered the case of random costs in (1.1) and used modified E-model for solving this problem. Bakhshi et al. [15] find the optimal Sample Numbers in Multivariate Stratified Sampling with a Probabilistic cost constraint in (1.2).
random in (1.1)) has been dealt with Diaz-Garcia and Garay Tapia [13]. Javed et al. [14] considered the case of random costs in (1.1) and used modified E-model for solving this problem. Bakhshi et al. [15] find the optimal Sample Numbers in Multivariate Stratified Sampling with a Probabilistic cost constraint in (1.2).
Here we consider the case of a non-linear cost function with random coefficients. The equivalent deterministic model for the problem in (1.1) is obtained by applying the chance constrained programming technique. The result of optimal allocation using Chance Constrained programming when the weighted sum of variances of the estimates of various characters is minimized is compared through a numerical example with the proportional allocation. The model in (1.2) with non-linear cost function in constraints is handled by using the modified-E model of Diaz-Garcia and Garay Tapia [13]. The results are applied to a simulated example.
2. Problem Formulation
We consider a multivariate population consisting of N units which is divided into L disjoint strata of sizes
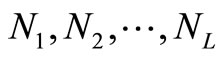 such that
such that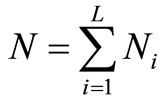 . Suppose that
. Suppose that 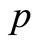
characteristics  are measured on each unit of the population. We assume that the strata boundaries are fixed in advance. Let
are measured on each unit of the population. We assume that the strata boundaries are fixed in advance. Let  units be drawn according to a stratified simple random sampling plan without replacement from the
units be drawn according to a stratified simple random sampling plan without replacement from the  stratum
stratum 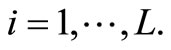 For
For 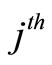 character, an unbiased estimate of the population mean
character, an unbiased estimate of the population mean 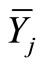
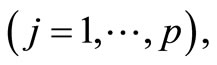 denoted by
denoted by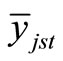 , has its sampling variance
, has its sampling variance
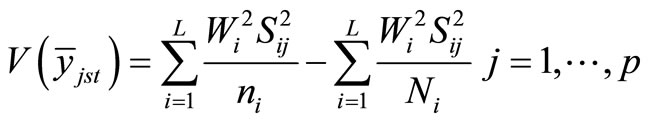 (2.1)
(2.1)
where 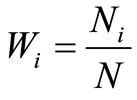 is the stratum weight and
is the stratum weight and  is the variance for the
is the variance for the 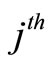
character in the 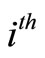 stratum. Let
stratum. Let  be the upper limit on the total cost of the survey. The problem of optimal sample allocation involves determining the sample sizes
be the upper limit on the total cost of the survey. The problem of optimal sample allocation involves determining the sample sizes  that minimize the variances of various characters under the given sampling budget C. Within any stratum the linear cost function is appropriate when the major item of cost is that of taking the measurements on each unit. If travel costs between units in a given stratum are substantial, empirical and mathematical studies indicate that the costs are better represented by the expression
that minimize the variances of various characters under the given sampling budget C. Within any stratum the linear cost function is appropriate when the major item of cost is that of taking the measurements on each unit. If travel costs between units in a given stratum are substantial, empirical and mathematical studies indicate that the costs are better represented by the expression , where
, where 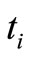 is the travel cost incurred in enumerating a sample unit in the
is the travel cost incurred in enumerating a sample unit in the  stratum, see Beardwood et al. [16], who observe that the distance between
stratum, see Beardwood et al. [16], who observe that the distance between 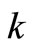 randomly scattered points is proportional to
randomly scattered points is proportional to . Assuming this non-linear cost function one should have
. Assuming this non-linear cost function one should have
 (2.2)
(2.2)
where 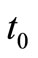 is the overhead cost.
is the overhead cost.
The restrictions on the sample sizes from various strata are
 (2.3)
(2.3)
Ignoring the constant term in (2.1), the allocation problem with non-linear cost function can be written as the following p convex programming problems
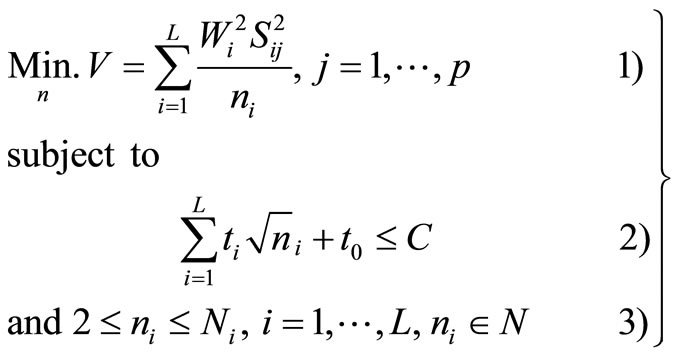 (2.4)
(2.4)
In many practical situations the travel costs  in the various strata are not fixed and may be considered as random. Let us assume that
in the various strata are not fixed and may be considered as random. Let us assume that ,
, 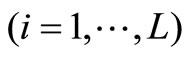 are independently normally distributed random variables.
are independently normally distributed random variables.
So, we write the above problem in the following chance constrained programming form (see, charnes & cooper [17])
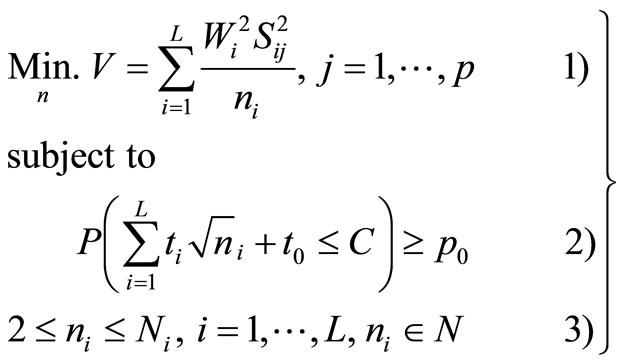 (2.5)
(2.5)
where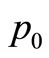 ,
, 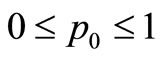 is a specified probability.
is a specified probability.
3. Solution Using Chance Constrained Programming
Let us assume that the costs ,
,  in the constraint function (2.5 2)) are independently and normally distributed random variables. Let
in the constraint function (2.5 2)) are independently and normally distributed random variables. Let 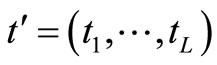 and
and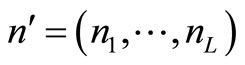 . Then the function
. Then the function  will also be normally distributed with mean
will also be normally distributed with mean  and variance
and variance .
.
The mean of the function  is obtained as
is obtained as
 (3.1)
(3.1)
where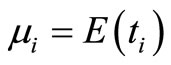 ,
,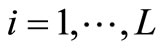 .
.
The variance is obtained as
 (3.2)
(3.2)
where 
 .
.
Now let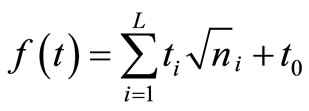 , then {2.5 2)} is given by
, then {2.5 2)} is given by  which is equivalent to
which is equivalent to
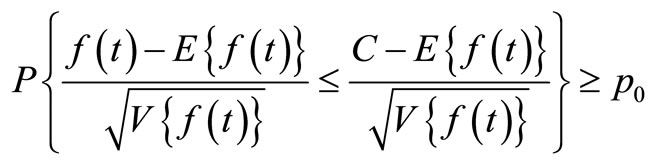 where
where  is a standard normal variable with mean zero and variance one. Thus the probability of realizing
is a standard normal variable with mean zero and variance one. Thus the probability of realizing 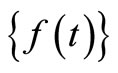 less than or equal to C can be written as
less than or equal to C can be written as
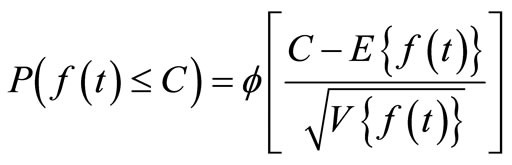 (3.3)
(3.3)
where  represents the cumulative density function of the standard normal variable evaluated at z. If
represents the cumulative density function of the standard normal variable evaluated at z. If  represents the value of the standard normal variable at which
represents the value of the standard normal variable at which , then the constraint (3.3) can be written as
, then the constraint (3.3) can be written as
 (3.4)
(3.4)
The inequality (3.4) will be satisfied only if

or equivalently,
 (3.5)
(3.5)
Substituting from (3.1) and (3.2) in (3.5), we get
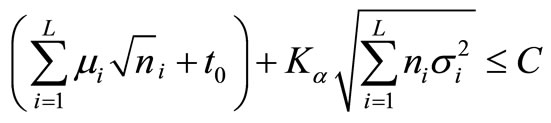 (3.6)
(3.6)
The constants 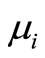 and
and  in (3.6) are unknown (by hypothesis). So we will use the estimators of mean
in (3.6) are unknown (by hypothesis). So we will use the estimators of mean
 and variance
and variance  given by
given by
 (3.7)
(3.7)
 (3.8)
(3.8)
where  and
and  are the estimated means and variances from the sample.
are the estimated means and variances from the sample.
Thus, an equivalent deterministic constraint to the stochastic constraint is given by
 (3.9)
(3.9)
The equivalent deterministic non-linear programming problem to the stochastic programming problem (2.5) is given by
 (3.10)
(3.10)
A compromise solution to these  problems can be obtained by assigning the weights to various characters according to some measure of their importance, see Khan et al. [18]. It is assumed that the characteristics are mutually independent so that the co-variances are zero. Let
problems can be obtained by assigning the weights to various characters according to some measure of their importance, see Khan et al. [18]. It is assumed that the characteristics are mutually independent so that the co-variances are zero. Let 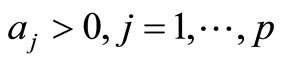 be the weights assigned to various characteristics according to some measure of their importance. If the population means of various characteristics are of interest, it may be a reasonable criterion for obtaining the compromise allocation to minimize the weighted sum
be the weights assigned to various characteristics according to some measure of their importance. If the population means of various characteristics are of interest, it may be a reasonable criterion for obtaining the compromise allocation to minimize the weighted sum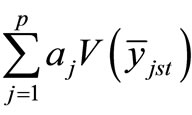 . It is conjectured that weights
. It is conjectured that weights
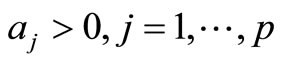 should be proportional to the sum of the stratum variances for
should be proportional to the sum of the stratum variances for  characteristics, that is
characteristics, that is
 ,
,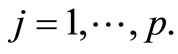
Letting  the above conjecture leads to
the above conjecture leads to

Then the deterministic non-linear programming problem with a single compromise objective function is
 (3.11)
(3.11)
The non-linear programming problem in (3.11) is convex as the objective function in {3.11 1)} is convex, see Kokan and Khan [7] and the left hand side in {3.11 2)} is also convex. So it is possible to solve the convex programming problem (CPP) (3.11) by using any standard convex programming algorithm. The optimal sample numbers thus obtained may turn out to be fractional. However, it is known that the variance functions are flat at the optimum solution. So for large sample size it is enough to round the fractional values to the nearest integers. However, for small n an integer solution can be obtained by using branch and bound method.
4. Modified E-Model
Let us consider the situation in which the survey is to be conducted in such a way that the budget of the survey for all the p characters is minimized for given upper limits on the variances. The non-linear cost function of modified E-model is given by 
where  and
and 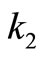 are the non-negative constant whose values indicate the relative importance of
are the non-negative constant whose values indicate the relative importance of 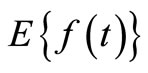 and
and  for minimization. From (3.7) and (3.8) we have
for minimization. From (3.7) and (3.8) we have
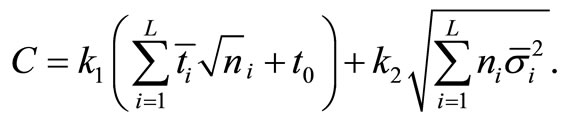 (4.1)
(4.1)
Now let the upper limits fixed for the variance of  character be
character be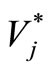 ,
, 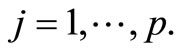
The precision constraints are then given by
 (4.2)
(4.2)
Using Modified E-model technique, the problem is formulated as
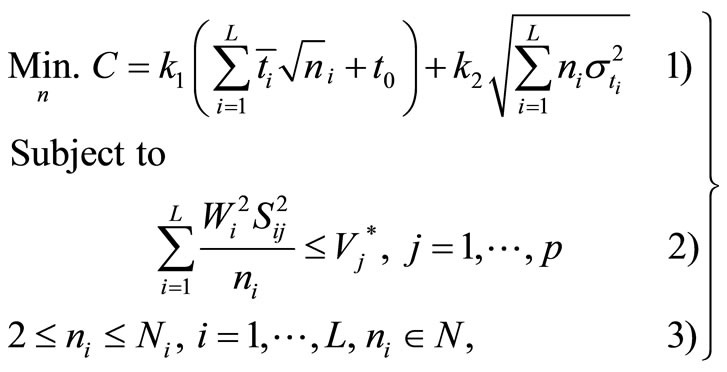 (4.3)
(4.3)
where  and
and 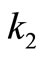 are non-negative constants, and their values show the relative importance of the expectation and the variance. Some authors suggest that
are non-negative constants, and their values show the relative importance of the expectation and the variance. Some authors suggest that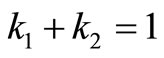 , see Rao ([19], p. 599).
, see Rao ([19], p. 599).
Remarks
1) If we take  and
and 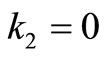 in the problem (4.3), the resulting model is known as the E-model, see Uryasev and Pardalos [20]. For E-model the objective function (4.3) reduces to
in the problem (4.3), the resulting model is known as the E-model, see Uryasev and Pardalos [20]. For E-model the objective function (4.3) reduces to
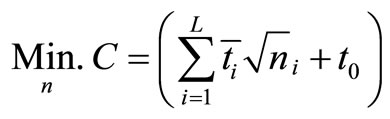
2) If we take 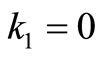 and
and 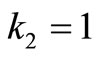 in (4.3), the resulting model is known as the V-model. For V-model the objective function in (4.3) reduces to
in (4.3), the resulting model is known as the V-model. For V-model the objective function in (4.3) reduces to
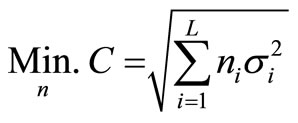
5. Numerical Illustration
The following numerical example demonstrates the use of the solution procedure. The data used in this example is from a stratified random sample survey conducted in Varanasi district of Uttar Pradesh (U.P), India to study the distribution of manurial resources among different crops and cultural practices (see Sukhatme et al. [21]). Relevant data with respect to the two characteristics “area under rice” and “total cultivated area” in the district are given in Table 1. The total number of villages in the district was 4190.
In order to demonstrate the procedure the following are also assumed. The per unit travel costs ,
, 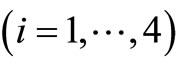 of measurement in various strata are independently normally distributed with the following means and variances
of measurement in various strata are independently normally distributed with the following means and variances  = 3,
= 3,  = 4,
= 4,  = 5,
= 5,  = 7 and
= 7 and 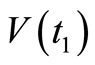 = 0.6,
= 0.6,  = 0.5,
= 0.5, 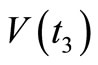 = 0.7,
= 0.7,  = 0.8.
= 0.8.
The total amount available for the survey C is assumed as 300 units including an expected overhead cost  = 25 units.
= 25 units.
5.1. Minimization of the Variances Subject to the Non-Linear Cost Function
Let the chance constraint 2.5 2) be required to be satisfied with 99% probability. Then  is such that
is such that 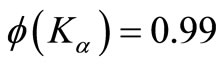 . The value of standard normal variable
. The value of standard normal variable  corresponding to 99% confidence limits is 2.33. Thus, the (non-linear programming) problem (3.11) is obtained as
corresponding to 99% confidence limits is 2.33. Thus, the (non-linear programming) problem (3.11) is obtained as
 (5.1)
(5.1)
NLP problem (5.1) is solved by using LINGO computer program a package for constrained optimization by LINDO systems Inc, see LINGO users Guide [22].
The solution obtained is  = 624.23,
= 624.23,  = 37.27,
= 37.27,  = 33.04 and
= 33.04 and 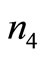 = 172.80 with objective function value
= 172.80 with objective function value 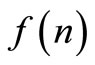 = 44.57. The integer solution is
= 44.57. The integer solution is 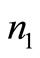 = 623,
= 623, 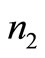 = 37,
= 37,  = 34 and
= 34 and 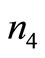 = 172 with value of the objective function
= 172 with value of the objective function  = 44.58.
= 44.58.
In the numerical illustration presented above the total sample size is 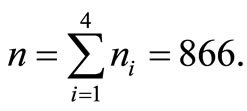 As suggested by Neyman [1], if proportional allocation is used, with
As suggested by Neyman [1], if proportional allocation is used, with  and values
and values  as given in Table 1, we get the sample sizes
as given in Table 1, we get the sample sizes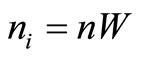 ; i = 1, 2, 3 and 4 as:
; i = 1, 2, 3 and 4 as:
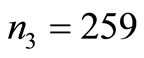
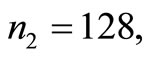
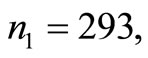 and
and 
Note that the left hand side of the cost constraint in (5.1) from proportional allocation is obtained as 286.62. so that it is badly violated.
Further, under the proportional allocation the weighted sum of variances is worked out as:
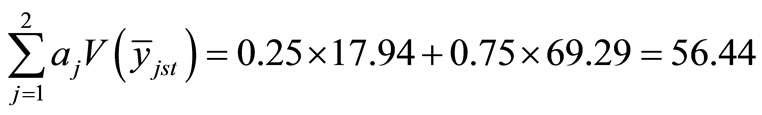
which is much more greater than the minimum value 44.58 obtained through compromise allocation.
5.2. Minimization of the Cost Subject to Bounds on Variances
In the above example let us minimize the cost restricted to given upper limits on variances. Then, using the modified E-model technique with given upper limits on the variances as ,
, 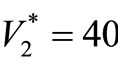 and taking
and taking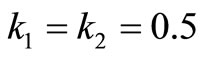 , we solve the following NLP problem from (4.3):
, we solve the following NLP problem from (4.3):
The solution obtained is  = 681,
= 681, 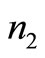 = 32,
= 32,  = 23 and
= 23 and 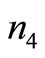 = 150 with the value of the objective function as C = 117.15.
= 150 with the value of the objective function as C = 117.15.
The total sample size turns out to be 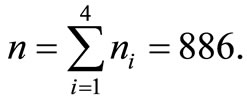
For proportional allocation, with 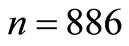 and the values
and the values  as given in Table 1 we get the sample sizes as:
as given in Table 1 we get the sample sizes as:
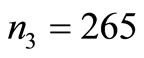
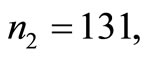
 and
and 
Under the proportional allocation the min cost is obtained as C = 149.88. Also the constraints in (5.2) are not satisfied by the allocation.
6. Conclusion
We have considered the allocation problem in multivariate stratified surveys as a problem of non-linear stochastic programming with non linear cost function. We have proposed the Chance Constrained programming technique and the technique of modified E-model for their
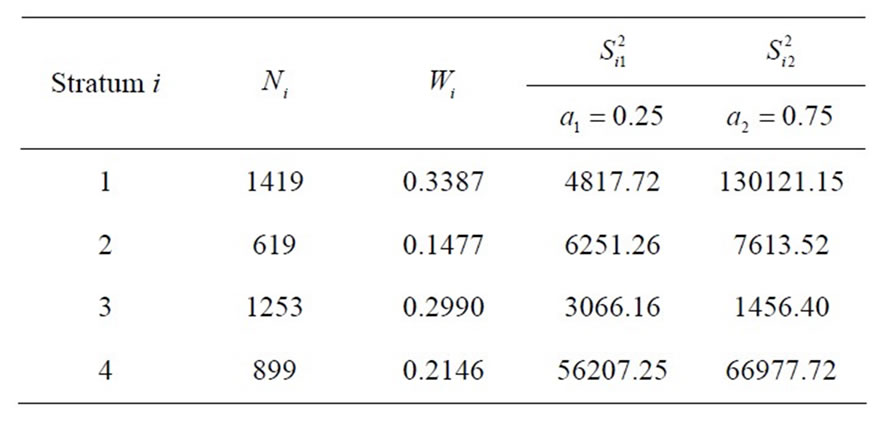
Table 1. Data for four strata and two characteristics.
solutions. These techniques are then used on a numerical example in Section 5. The respective solutions obtained are seen much better even for the non-linear cost function in the constraints than the corresponding solutions with proportional allocation.
REFERENCES
- J. Neyman, “On the Two Different Aspects of the Representative Method: The Method of Stratified Sampling and the Method of Purposive Selection,” Journal of the Royal Statistical Society, Vol. 97, No. 4, 1934, pp. 558-625. doi:10.2307/2342192
- T. Dalenius, “Sampling in Sweden: Contributions to the Methods and Theories of Sample Survey Practice,” Almqvist Och Wiksell, Stockholm, 1957.
- S. P. Ghosh, “A Note on Stratified Random Sampling with Multiple Characters,” Calcutta Statistical Association Bulletin, Vol. 8, 1958, pp. 81-89.
- F. Yates, “Sampling Methods for Censuses and Surveys,” 3rd Edition, Charles Griffin and Co., London, 1960.
- H. Aoyama, “Stratified Random Sampling with Optimum Allocation for Multivariate Populations,” Annals of the Institute of Statistical Mathematics, Vol. 14, No. 1, 1963, pp. 251-258. doi:10.1007/BF02868647
- J. L. Folks and C. E. Antle, “Optimum Allocation of Sampling Units to the Strata When There Are R Responses of Interest,” Journal of the American Statistical Association, Vol. 60, No. 309, 1965, pp. 225-233. doi:10.2307/2283148
- A. R. Kokan and S. U. Khan, “Optimum Allocation in Multivariate Surveys: An Analytical Solution,” Journal of the Royal Statistical Society, Series B, Vol. 29, 1967, pp. 115-125.
- S. Chatterji, “Multivariate Stratified Surveys,” Journal of the American Statistical Association, Vol. 63, No. 322, 1968, pp. 530-534. doi:10.2307/2284023
- M. J. Ahsan and S. U. Khan, “Optimum Allocation in Multivariate Stratified Random Sampling Using Prior Information,” Journal of Indian Statistical Association, Vol. 15, 1977, pp. 57-67.
- N. Jahan, M. G. M. Khan and M. J. Ahsan, “A Generalized Compromise Allocation,” Journal of Indian Statistical Association, Vol. 32, No. 2, 1994, pp. 95-101.
- M. G. M. Khan, M. J. Ahsan and N. Jahan, “Compromise Allocation in Multivariate Stratified Sampling: An Integer Solution,” Naval Research Logistics, Vol. 44, No. 1, 1997, pp. 69-79. doi:10.1002/(SICI)1520-6750(199702)44:1<69::AID-NAV4>3.0.CO;2-K
- A. Prekopa, “Stochastic Programming,” Series Mathematics and Its Applications, Kluwer Academic Publishers, Berlin, 1995.
- J. A. Diaz Garcia and M. M. Garay Tapia, “Optimum Allocation in Stratified Surveys: Stochastic Programming,” Computational Statistics and Data Analysis, Vol. 51, No. 6, 2007, pp. 3016-3026. doi:10.1016/j.csda.2006.01.016
- S. Javed, Z. H. Bakhshi and M. M. Khalid, “Optimum Allocation in Stratified Sampling with Random Costs,” International Review of Pure and Applied Mathematics, Vol. 5, No. 2, 2009, pp. 363-370.
- Z. H. Bakhshi, M. F. Khan and Q. S. Ahmad, “Optimal Sample Numbers in Multivariate Stratified Sampling with a Probabilistic Cost Constraint,” International Journal of Mathematics and Applied Statistics, Vol. 1, No. 2, 2010, pp. 111-120.
- J. Beardwood, J. H. Halton and J. M. Hammersley, “The Shortest Path through Many Points,” Mathematical Proceedings of the Cambridge Philosophical Society, Vol. 55, No. 4, 1959, pp. 299-327. doi:10.1017/S0305004100034095
- A. Charnes and W. W. Cooper, “Chance Constrained Programming,” Management Science, Vol. 6, No. 1, 1959, pp. 73-79. doi:10.1287/mnsc.6.1.73
- E. A. Khan, M. G. M. Khan and M. J. Ahsan, “On Compromise Allocation in Multivariate Stratified Sampling,” Aligarh Journal of Statistics, Vol. 23, 2003, pp. 31-47.
- S. S. Rao, “Optimization-Theory and Applications,” Wily Eastern Limited, New Delhi, 1979.
- S. Uryasev and P. M. Pardalos, “Stochastic Optimization,” Kluwer Academic Publishers, Dordrecht, 2001.
- P. V. Sukhatme, B. V. Sukhatme, S. Sukhatme and C. Asok, “Sampling Theory of Surveys with Applications” 3rd Edition, Iowa State University Press, Ames, 1984.
- Lindo Systems Inc., “LINGO User’s Guide,” Lindo Systems Inc., Chicago, 2001.
NOTES
*Corresponding author.

