Paper Menu >>
Journal Menu >>
 Wireless Sensor Network, 2010, 2, 37-42 doi:10.4236/wsn.2010.21005 anuary 2010 (http://www.SciRP.org/journal/wsn/). Copyright © 2010 SciRes. WSN Published Online J A Method for Rapid Matching Based on Second Order Partial Derivative Haiyan YU, Zhiquan ZHOU, Zhanfeng ZHAO, Xiaolin QIAO School of Electronics and Information Technology, Harbin Institute of Technology, Harbin, China Email: hit_yhy@sina.com Received September 17, 2009; revised October 28, 2009; accepted Octob er 30, 2009 Abstract Our goal is to enhance matching speed which is important for image engineering. Second Partial Derivative operator in Harris corner detector is directly used to compute the similarity between corners. Then initial matches are obtained. The algorithm is contrasted with normalized cross-correlation and method based on horizontal and vertical gradient. Its computational complexity is reduced and matching speed is improved effectively because this method only adopts the addition and subtraction operations. Experiments on several real images test the matching speed, the matching precision and matching rate of the algorithm. The results demonstrate that the algorithm not only have higher speed but also get higher matching precision and correct matching rate. Even though the stereo image pairs have brightness differences, it still performs rather well. Keywords: Corner Matching, Gradient Operator, Similarity 1. Introduction Feature matching is to establish the correspondence be- tween feature points of left and right image in a stereo image pair. It is an important step in computer vision applications, such as stereo vision, motion tracking, and identification. During this process, matching speed is very important for real-time application of image proc- essing. Corner is a most widely used feature for matching be- cause of its good performance against the change of per- spective and easy to detect. The common approach for corner matching is to take a small region of pixels (re- ferred to as a correlation window) from around the de- tected corner and compare it with a similar region from around each of the candidate corners in the other image [1]. We can find that matching time usually depends on initial matching method. There are several ways based on gray information to complete the initial matching, nor- malized cross correlation (NCC), sum of squared differ- ence (SSD), and sum of absolute difference (SAD). The most popular measure of similarity is the normalized cross correlation. Though a lot of algorithms have been presented in the past, establishing good corners correspondences between stereo pairs is still a very challenging task for a number of reasons such as distortion, the difference in lighting condition, and transformations (rotation, translation, scaling). It is the main object of matching to cost short time and get high matching accuracy at the same time. In this paper a new corner matching algorithm based on gradient is proposed. Gradient information is widely used in feature matching based on edge, however, cor- ners are also pixels in which gradient change greatly, so that gradient information also can be used in initial matching. In recent years, the horizontal and vertical gradients have been used to measure the similarity be- tween corners [2,3], the horizontal and vertical gradients directly obtained in corner detector need no additional computation, but adopting two gradient operators in- creases computational complexity. In our algorithm, only one gradient operator, Second Order Partial Derivative, which includes horizontal and vertical gradient informa- tion, is found, and it can be directly obtained in corner detector. We replace horizontal and vertical gradient op- erators with one Second-Order-Derivative operator. It makes our algorithm simple and have high speed. The traditional way to compute the similarity between two corners is normalized intens ity cross-correlation. In order to raise computational speed further, we adopt the sum of absolute differences instead of complex normalized cross-correlation. The proposed algorithm not only has high speed but also gets high matching precision and matching rate. Experimental results suggest that it is practicable, effective and robust.  H. Y. YU ET AL. 38 Our proposed method for corner matching is com- posed of three main steps (1) corner extraction, (2) initial matching based on gradient and (3) matching refinement. In step (2), our algorithm is compared with NICC and GXGY. In the following subsection, each step is de- scribed in detail. 2. Corners Extraction The choice of corner detector has a large impact on the results of a given matching scheme. A number of algo- rithms for corner extraction have been presented in re- cent years [4,5]. Because of good performance of the well known Harris corner detector [6], it is chosen to extract interest points in our algorithm. The original Har- ris corner detector calculates the value of Equation (1): 2 22 2 22 1exp 22 x xy xy y GGG xy cGG G x xxy x yyy GG GG (1) The operator states a rotational invariance. Here I denotes the gray level, x G denotes its gradient in x axis, ; denotes its gradient in axis, . The eigenvalues 10 10 10 x GI y GI 1 1 1 G 111 00 111 y 0 y1 and 2 of are the main curvatures of its auto-correlation. c The corner detector in application is: det( )( ) H ctrace c (2) In the above equation, the parameter is tradition- ally set to 0.004, 12 det c , c12 trace . To avoid large locality excursion of corners detected, we adopt the modified Harris corner detector [7], which is given by det det trace c Mtrace c (3) This operator means filtering the numerater with Gaussian function of less det , but filtering the de- nominator with Gaussian function which has largertrace , so we can get accurate localization and much better sta- bility. 3. Initial Matching Based on Second Order Derivative Initial matching is usually to measure the similarity be- tween two image regions. There are many measures of similarity, of which only a few of most popular are con- sidered here. 1) NICC The traditional way to compute the similarity between two corners is Normalized Intensity Cross Correlation (NICC) which is computed as follows: ' '' ' ' 2' (, ) [1( )1][2()2] [1( )1][2()2] m blockP m blockQ m blockPm blockP m blockQm blockQ NICC MM imii mi imii mi 2 (4) In the above equation, M and ' M are two sets of corners to be compared, P and Q blocks (referred to as a correlation window) are two windows centered on position of each corner, usually =7, 9, 11 or 13, and are pixels within P and Q blocks. and are intensity values, m 2( ' m1( )im ')im 1i, 2i are the mean (aver- age intensity values) of the two correlation windows. Correlation operation includes multiplication and divi- sion which cost much time. And Gray correlation has low accuracy which would introduce error matching. 2) GXGY Two gradient operator x G and are used to compute the similarity [2,3] which can reduce error matching points between two corners. It is computed as follows: y G ' '' (, )()() xx m blockP m blockQ GXMMGm Gm (5) ' '' (, )()() yy mblockP mblockQ GYMMGm Gm (6) GXGYGX GY (7) x G and include gr ay gradien t information which can reduce error matching point. And y G x G and can be acquired from the procedure of corner extraction, so it will reduce matching time. y G 3) Algorithm of this paper——GXY According above analysis, we know that gradient in- formation can get more right matching point. In the Equation (1), Second Order Partial Derivative x y G for each corner has been obtained. And x y G gradient op- Copyright © 2010 SciRes. WSN  H. Y. YU ET AL. 39 erator contains the horizontal and vertical gradient in- formation, so it is valuable. We describe each corner with x y G. During the matching process, each corner at , x y in the first image is compared with a set of potential corners in the other image, located within a x y dd rectangular window centered on , x y, where x dand are the maximum expected disparity in horizontal and vertical axes, respectively. Corners are compared using the sum of absolute differences which is computed as follows: y d ' ' (, )()() xy xy m blockP m blockQ ' YMMGmG m GX (8) Only corners that have minimal GX value with each other are considered as a pair of initial matching corners. Obviously, because of only addition and sub- traction operations included the Equation (8) is simpler than that of the Equation (4). So GXY method will cost less time than NICC. And it also has well accuracy than NICC because of using gradient information. Y Compared with GXGY, GXGY computes two group of the sum of absolute differences cost two times of time so that computational complexity is increased. From comparison and analysis in above, we can get conclusion that the method GXY of computing the simi- larity can reduce computational complexity effectively. 4. Matching Refinement Based on the result of initial matching, in this section, we use epipolar constraint to remove the outliers. The epipolar geometry is the intrinsic projective ge- ometry between two views. It is independent of scene structure, and only depends on the internal parameters and relative pose of cameras. This intrinsic geometry is included in the fundamental matrix F. For any pair of corresponding corners x and , x in the two images, this relation should be satisfied: '0 T xFx (9) In this paper, the fundamental matrix is calculated by the eight-point algorithm [8] which needs at least 8 points. We use RANSAC (Random Sample Consensus) algorithm [9] to robustly fit a fundamental matrix to a set of putatively matched corners. Given matched cor- ner pairs, the RANSAC algorithm involves the random selection pairs, computation of the fundamental ma- trix (as described in above section), and determining to what degree all the available matches support the epipo- lar constraint. After fitting a fundamental matrix, mis- matched corners can be rejected effectively so that we obtain final matching corners from initial matches. N p 5. Experiments The proposed algorithm has been extensively evaluated using several groups of image pairs and multi-views. Our experiments are carried out on Pentium 4 with 2.8GHZ processor and 758MB memory, the software used is MATLAB 6.5. The matching results are shown in figures and tables as follows. GXY denotes the algorithm proposed in this paper; GXGY denotes the algorithm which use the horizontal and vertical gradients to measure the similarity between two corners (Equations (5) (6) (7)), NICC denotes the algorithm which use normalized intensity cross-correla- tion to measure the similarity between two corners (Equation (4)), other steps and parameters, for example, epipolar constraint and the value of correlation window, in these three algorithms are the same. All views size in this paper is 640 480 . In order to test the performance of GXY algorithm, we compared GXY with NICC and GXGY. The matching results are showed in following figures. The matching method, the number of corners extracted from the left and right images, the number of initial matches, the number of final matches, the average distance and the matching time are given in the successive columns of the tables. (Figure 1) (a) GXY (b) NICC (c) GXGY Figure 1. Final matching result and dele te d outliers. C opyright © 2010 SciRes. WSN 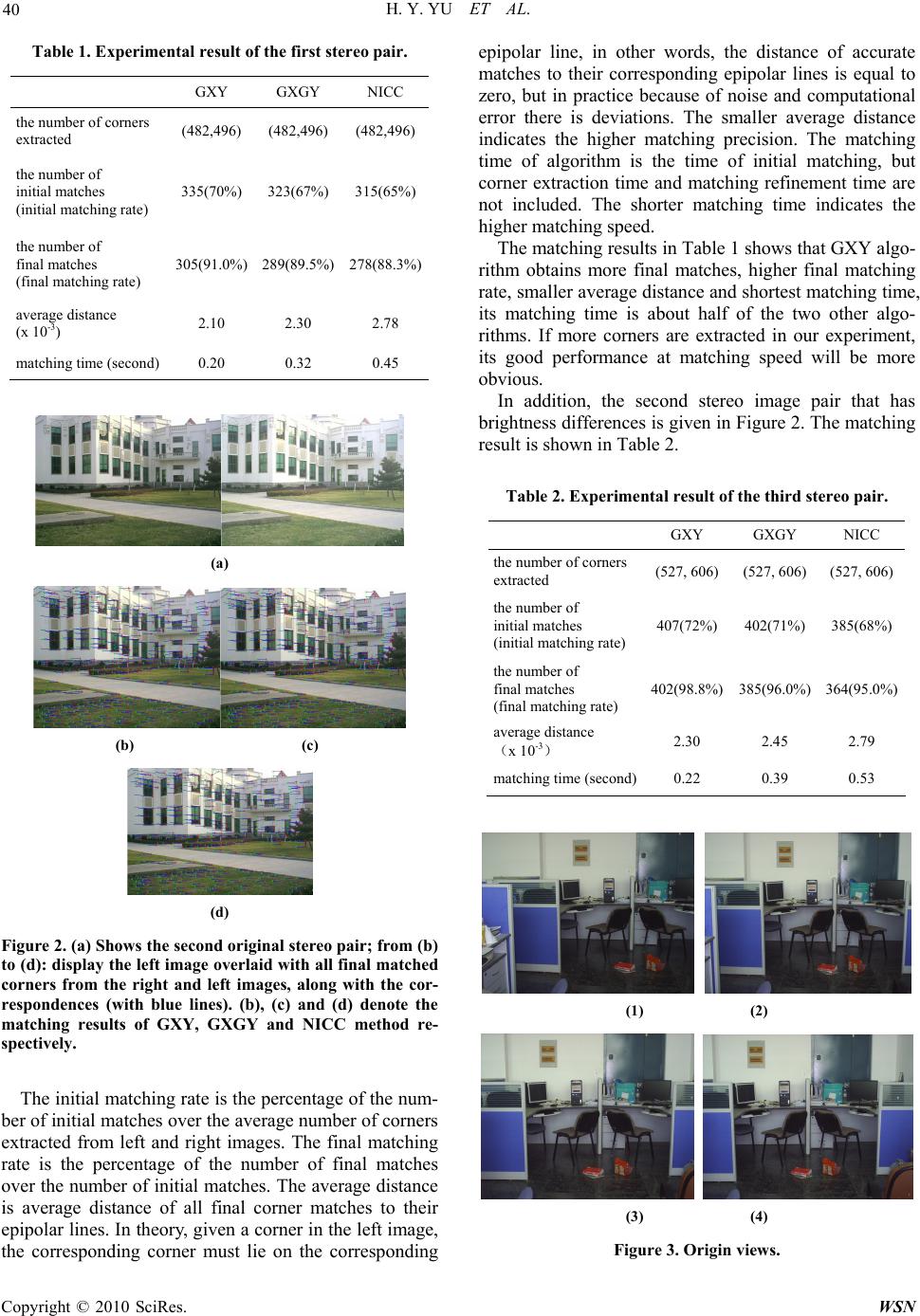 H. Y. YU ET AL. 40 Table 1. Experimental result of the first stereo pair. GXY GXGY NICC the number of corners extracted (482,496)(482,496) (482,496) the number of initial matches (initial matching rate) 335(70%)323(67%) 315(65%) the number of final matches (final matching rate) 305(91.0%) 289(89.5%) 278(88.3%) average distance (x 10-3) 2.10 2.30 2.78 matching time (second) 0.20 0.32 0.45 (a) (b) (c) (d) Figure 2. (a) Shows the second original stereo pair; from (b) to (d): display the left image overlaid with all final matched corners from the right and left images, along with the cor- respondences (with blue lines). (b), (c) and (d) denote the matching results of GXY, GXGY and NICC method re- spectively. The initial matching rate is the percentage of the num- ber of initial matches over the average number of corners extracted from left and right images. The final matching rate is the percentage of the number of final matches over the number of initial matches. The average distance is average distance of all final corner matches to their epipolar lines. In theory, given a corner in the left image, the corresponding corner must lie on the corresponding epipolar line, in other words, the distance of accurate matches to their corresponding epipolar lines is equal to zero, but in practice because of noise and computational error there is deviations. The smaller average distance indicates the higher matching precision. The matching time of algorithm is the time of initial matching, but corner extraction time and matching refinement time are not included. The shorter matching time indicates the higher matching speed. The matching results in Table 1 shows that GXY algo- rithm obtains more final matches, higher final matching rate, smaller average distance and shortest matching time, its matching time is about half of the two other algo- rithms. If more corners are extracted in our experiment, its good performance at matching speed will be more obvious. In addition, the second stereo image pair that has brightness differences is given in Figure 2. The matching result is shown in Table 2. Table 2. Experimental result of the third stereo pair. GXY GXGY NICC the number of corners extracted (527, 606) (527, 606) (527, 606) the number of initial matches (initial matching rate) 407(72%) 402(71%) 385(68%) the number of final matches (final matching rate) 402(98.8%) 385(96.0%) 364(95.0%) average distance (x 10-3) 2.30 2.45 2.79 matching time (second)0.22 0.39 0.53 (1) (2) (3) (4) Figure 3. Origin views. Copyright © 2010 SciRes. WSN 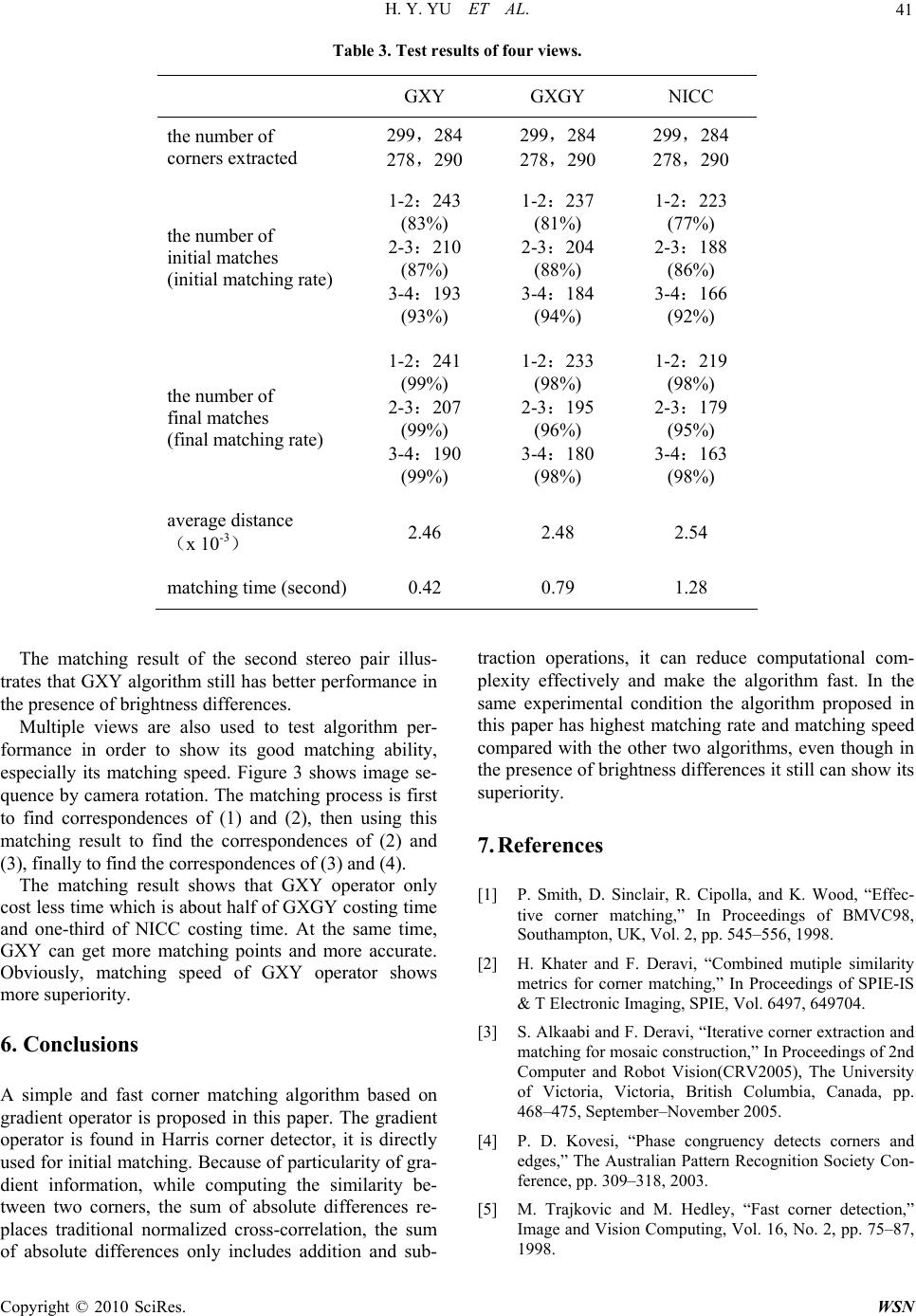 H. Y. YU ET AL. Copyright © 2010 SciRes. WSN 41 Table 3. Test results of four views. GXY GXGY NICC the number of corners extracted 299,284 278,290 299,284 278,290 299,284 278,290 the number of initial matches (initial matching rate) 1-2:243 (83%) 2-3:210 (87%) 3-4:193 (93%) 1-2:237 (81%) 2-3:204 (88%) 3-4:184 (94%) 1-2:223 (77%) 2-3:188 (86%) 3-4:166 (92%) the number of final matches (final matching rate) 1-2:241 (99%) 2-3:207 (99%) 3-4:190 (99%) 1-2:233 (98%) 2-3:195 (96%) 3-4:180 (98%) 1-2:219 (98%) 2-3:179 (95%) 3-4:163 (98%) average distance (x 10-3) 2.46 2.48 2.54 matching time (second) 0.42 0.79 1.28 The matching result of the second stereo pair illus- trates that GXY algorithm still has better performance in the presence of brightness differences. Multiple views are also used to test algorithm per- formance in order to show its good matching ability, especially its matching speed. Figure 3 shows image se- quence by camera rotation. The matching process is first to find correspondences of (1) and (2), then using this matching result to find the correspondences of (2) and (3), finally to find the correspondences of (3) and (4). The matching result shows that GXY operator only cost less time which is about half of GXGY costing time and one-third of NICC costing time. At the same time, GXY can get more matching points and more accurate. Obviously, matching speed of GXY operator shows more superiority. 6. Conclusions A simple and fast corner matching algorithm based on gradient operator is proposed in this paper. The gradient operator is found in Harris corner detector, it is directly used for initial matching. Because of particularity of gra- dient information, while computing the similarity be- tween two corners, the sum of absolute differences re- places traditional normalized cross-correlation, the sum of absolute differences only includes addition and sub- traction operations, it can reduce computational com- plexity effectively and make the algorithm fast. In the same experimental condition the algorithm proposed in this paper has highest matching rate and matching speed compared with the other two algorithms, even though in the presence of brightness differences it still can show its superiority. 7. References [1] P. Smith, D. Sinclair, R. Cipolla, and K. Wood, “Effec- tive corner matching,” In Proceedings of BMVC98, Southampton, UK, Vol. 2, pp. 545–556, 1998. [2] H. Khater and F. Deravi, “Combined mutiple similarity metrics for corner matching,” In Proceedings of SPIE-IS & T Electronic Imaging, SPIE, Vol. 6497, 649704. [3] S. Alkaabi and F. Deravi, “Iterative corner extraction and matching for mosaic construction,” In Proceedings of 2nd Computer and Robot Vision(CRV2005), The University of Victoria, Victoria, British Columbia, Canada, pp. 468–475, September–November 2005. [4] P. D. Kovesi, “Phase congruency detects corners and edges,” The Australian Pattern Recognition Society Con- ference, pp. 309–318, 2003. [5] M. Trajkovic and M. Hedley, “Fast corner detection,” Image and Vision Computing, Vol. 16, No. 2, pp. 75–87, 1998.  H. Y. YU ET AL. 42 [6] C. G. Harris and M. J. Stephens, “A combined corner and edge detector,” Proceedings Fourth Alvey Vision Con- ference, Manchester, pp. 147–151, 1988. [7] A. Noble, “Descriptions of image surfaces,” PhD thesis, Department of Engineering Science, Oxford University, pp. 45, 1989. [8] R. I. Hartley, “In defense of the 8-point algorithm,” IEEE Transactions on Pattern Analysis and Machine Intelli- gence, Vol. 19, No. 6, pp. 580–593, June 1997. [9] M. A. Fischler and R. C. Bolles, “Random sample con- sensus: A paradigm for model fitting with applications to image analysis and automated cartography,” Communi- cation of the ACM, Vol. 24, pp. 381–395, 1981. Copyright © 2010 SciRes. WSN |

