Int'l J. of Communications, Network and System Sciences
Vol.3 No.2(2010), Article ID:1273,7 pages DOI:10.4236/ijcns.2010.32026
A Modified T/2 Fractionally Spaced Coordinate Transformation Blind Equalization Algorithm
1School of Electrical Engineering and Information, Anhui University of Science and Technology, Huainan, China
2College of Electronic and Information Engineering, Nanjing University of Information Science and Technology, Nanjing, China
Email: guo-yecai@126.com
Received November 3, 2009; revised December 22, 2009; accepted December 30, 2009
Keywords: Blind Equalization; Underwater Acoustic Channel; Coordinate-Transformation; Fractionally Spaced Equalizer.
Abstract
When T/2 Fractionally Spaced blind Equalization Algorithm based Constant Modulus Algorithm (T/2-FSE-CMA) is employed for equalizing higher order Quadrature Amplitude Modulation signals (QAM), it has disadvantages of low convergence speed and large Mean Square Error (MSE). For overcoming these disadvantages, a Modified T/2 Fractionally Spaced blind Equalization algorithm based on Coordinate Transformation and CMA (T/2-FSE-MCTCMA) was proposed by analyzing the character of 16QAM signal constellations. In the proposed algorithm, real and imaginary parts of input signal of T/2 fractionally spaced blind equalizer are equalized, respectively, and output signals of equalizer are transformed to the same unit circle by coordinate transformation method, a new error function is defined after making coordinate transformation and used to adjust weight vector of T/2 fractionally spaced blind equalizer. The proposed algorithm can overcome large misjudgments of T/2 fractionally spaced blind equalization algorithm for equalizing multi-modulus higher order QAM. Simulation results with underwater acoustic channel models demonstrate that the proposed T/2-FSE-MCTCMA algorithm outperforms T/2 Fractionally Spaced blind Equalization algorithm based on Coordinate Transformation and CMA (T/2-FSE-CTCMA) and the T/2-FSE-CMA in convergence rate and MSE.
1. Introduction
In underwater acoustic communication system, blind equalization technique without training sequence is an important means to eliminate intersymbol interference (ISI) [1–5]. Among them, baud-spaced equalizer based on Constant Modulus Algorithm (BSE-CMA) has simple structure, but its convergence rate is slow and its steady error is large [6,7]. Whereas, fractionally-spaced equalizer based on constant modulus algorithm (FSE-CMA) is employed for equalizing constant modulus signal, its convergence rate is fast and its steady error is low [8–10]. When the FSE-CMA is used to equalize high-order QAM signal, it can produce large misjudgments and lead to large mean square error, because higher order QAM signal constellations distribute in the several known circles and its module value is not constant [11,12]. Therefore, intersymbol interference is not sufficiently eliminated.
In the paper, on the basis of analyzing the character of 16QAM signal constellations [13–15], T/2 fractionally-spaced equalizer, and the thought of coordinate transformation [16] real and imaginary parts of output signal of each sub-channel are equalized, respectively, a new constant modulus error function is defined after making coordinate transformation to output of each equalizer. A cost function based on this error function is given. Iterative formula of weight vector of T/2 fractionally-spaced equalizer is got by making the cost function minimization. Finally, a Modified T/2 Fractionally Spaced blind Equalization algorithm based on Coordinate Transformation and CMA (T/2-FSEMCTCMA) is established.
This paper is organized as follows. In Section 2, fractionally spaced blind equalization algorithm is described. In Section 3, the T/2-FSE-MCTCMA is proposed. The performance of the proposed T/2-FSE-MCTCMA is analyzed in Sections 4 and 5. Finally, some conclusions are obtained.
2. Fractionally Spaced Blind Equalization Algorithm
Relevant researches show that fractionally spaced equalizer is equivalent to multi-channel system model [17–19]. Its structure is shown in Figure 1 Input and output signals of this system have the same sampling rate.
In Figure 1, 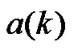 is the transmitted signal sequence and its sampling period is
is the transmitted signal sequence and its sampling period is ;
; 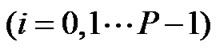
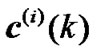 is an impulse response vector of the ith sub-channel and
is an impulse response vector of the ith sub-channel and
 ;
; 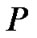 is fractionally spaced sampling factor;
is fractionally spaced sampling factor; 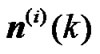 is an additive noise vector of the ith sub-channel;
is an additive noise vector of the ith sub-channel; 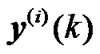 is an input signal vector of the ith blind equalizer and written as
is an input signal vector of the ith blind equalizer and written as
 (1)
(1)
where  is the length of impulse response vector of channel in baud spaced equalizer.
is the length of impulse response vector of channel in baud spaced equalizer.
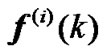 is the weight vector of the ith sub-equalizer and written as
is the weight vector of the ith sub-equalizer and written as
 (2)
(2)
where 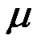 is defined as step size;
is defined as step size;  is an error function and given by
is an error function and given by
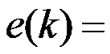 ;
; 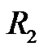 denotes module value of signals and given by
denotes module value of signals and given by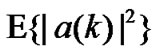
 .
.
The output signal of the whole system is given by
 (3)
(3)
where “*” denotes conjugate operator.
Fractionally Spaced blind Equalization algorithm based CMA(T/2-FSE-CMA)is only suitable to equalize constant modulus signals. When it is employed for equalizing multi-modulus QAM signal, it can easily produce large mean square error.
3. Modified T/2 Fractionally Spaced Coordinate Transformation Blind Equalization Algorithms
When the transmitted signal is higher order QAM signal, we make Figure 1 change in two aspects in order to obtain good equalization performance. At first, the real and imaginary parts of input signal 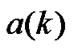 are equalized, respectively. It is equivalent to process real signals in the whole equalization process. Moreover, its computational complexity is decreased obviously comparison with that
are equalized, respectively. It is equivalent to process real signals in the whole equalization process. Moreover, its computational complexity is decreased obviously comparison with that

Figure 1. The structure of fractionally spaced blind equalizer.

Figure 2. The structure of a modified T/2 fractionally spaced coordinate transformation blind equalizer.
of the complex signals. The second, two error functions are defined after making coordinate transformation to the real and imaginary parts of output signal  and the cost functions based on these two error functions are obtained. Accordingly, the updating formula of weight vector of modified equalizer is given by making the cost function minimization. The structure diagram of the modified equalizer is shown in Figure 2. We call the modified equalizer as T/2-FSE-MCTCMA(Modified T/2 Fractionally Spaced blind Equalization algorithm based on Coordinate Transformation and CMA. In the proposed T/2-FSE-MCTCMA, according to Figure 2, the channel is divided into odd sub-channel
and the cost functions based on these two error functions are obtained. Accordingly, the updating formula of weight vector of modified equalizer is given by making the cost function minimization. The structure diagram of the modified equalizer is shown in Figure 2. We call the modified equalizer as T/2-FSE-MCTCMA(Modified T/2 Fractionally Spaced blind Equalization algorithm based on Coordinate Transformation and CMA. In the proposed T/2-FSE-MCTCMA, according to Figure 2, the channel is divided into odd sub-channel 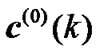 and even sub-channel
and even sub-channel , and
, and 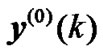 and
and 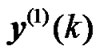 are input signals of each equalizer in the T/2-FSE-MCTCMA and written as
are input signals of each equalizer in the T/2-FSE-MCTCMA and written as
 (4)
(4)
 (5)
(5)
For sub-channel , its has real and imaginary equalizer. The weight vectors of the real and imaginary equalizer are expressed as
, its has real and imaginary equalizer. The weight vectors of the real and imaginary equalizer are expressed as  and
and , respectively, and
, respectively, and ,
,  are output signals of the real and imaginary equalizer. As for sub-channel
are output signals of the real and imaginary equalizer. As for sub-channel , the weight vectors of real and imaginary equalizer are expressed as
, the weight vectors of real and imaginary equalizer are expressed as  and
and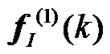 , the output signals of the real and imaginary equalizer are expressed
, the output signals of the real and imaginary equalizer are expressed 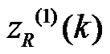 and
and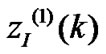 , respectively. The real part of the final output is written as
, respectively. The real part of the final output is written as
 (6)
(6)
The imaginary part of the final output is written as
 (7)
(7)
The final output signal of the equalizer is written as
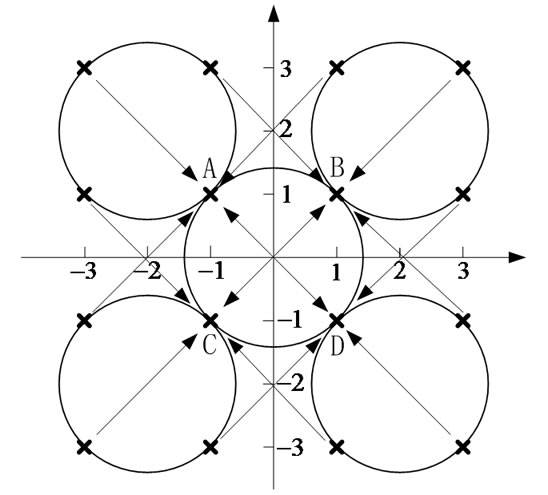
Figure 3. The coordinate transformation of 16 QAM signals.
 (8)
(8)
In the process of equalization, coordinate transformation method is introduced into blind equalization algorithm, the principle diagram of the coordinate transformation is shown in Figure 3.
In Figure 3, “ ” denotes ideal 16 QAM signal points after equalization, these points distribute in four known circles. We can make ideal 16 QAM signal points become four points A, B, C, and D via making coordinate transformation to output signals of the real and imaginary equalizer. A, B, C, and D must distribute in a circle.
” denotes ideal 16 QAM signal points after equalization, these points distribute in four known circles. We can make ideal 16 QAM signal points become four points A, B, C, and D via making coordinate transformation to output signals of the real and imaginary equalizer. A, B, C, and D must distribute in a circle.
When the CMA is used to equalize 16QAM signal, the error function is written as  (
(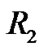 is a specific module value). Even if the channels are equalized completely, the error
is a specific module value). Even if the channels are equalized completely, the error  is not zero. This affects equalization results. So, coordinate transformation method is used to make 16QAM signal points in different circles turn into A, B, C, D four points in the same circle. In other words, after multi-modulus 16QAM signals is become constant modulus 4QAM signals, the error is zero under the condition that the channels are equalized completely. The performance of the algorithm based on coordinate transformation method (T/2-FSEMCTCMA) is optimal.
is not zero. This affects equalization results. So, coordinate transformation method is used to make 16QAM signal points in different circles turn into A, B, C, D four points in the same circle. In other words, after multi-modulus 16QAM signals is become constant modulus 4QAM signals, the error is zero under the condition that the channels are equalized completely. The performance of the algorithm based on coordinate transformation method (T/2-FSEMCTCMA) is optimal.
In Figure 2, 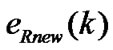 and
and  are the error function of the real and imaginary part after coordinate transformation, respectively, and defined as
are the error function of the real and imaginary part after coordinate transformation, respectively, and defined as
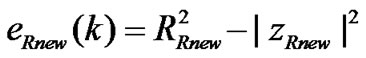 (9)
(9)
 (10)
(10)
where
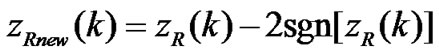 (11)
(11)
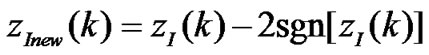 (12)
(12)
 (13)
(13)
 (14)
(14)
The updating formula of weight vector of the real and imaginary equalizer are written as
 (15)
(15)
 (16)
(16)
The final output signal of equalizer is written as
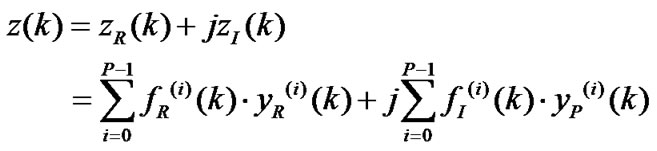 (17)
(17)
 (a)
(a) (b)
(b) (c)
(c) (d)
(d)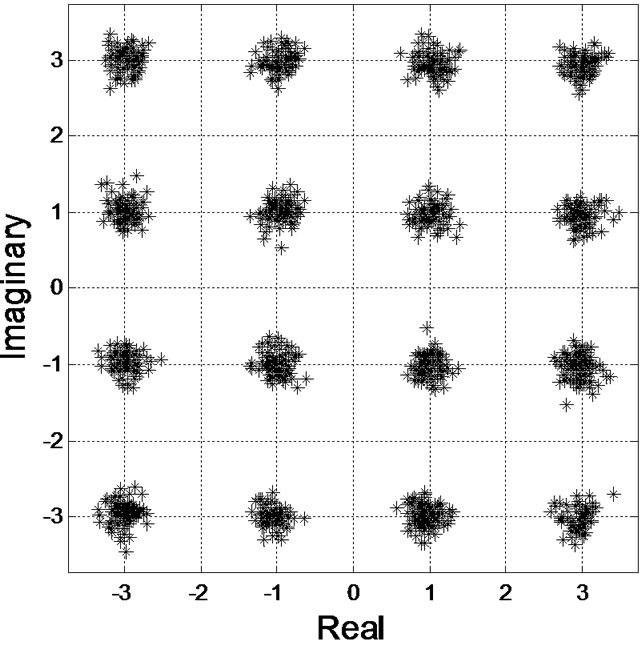 (e)
(e)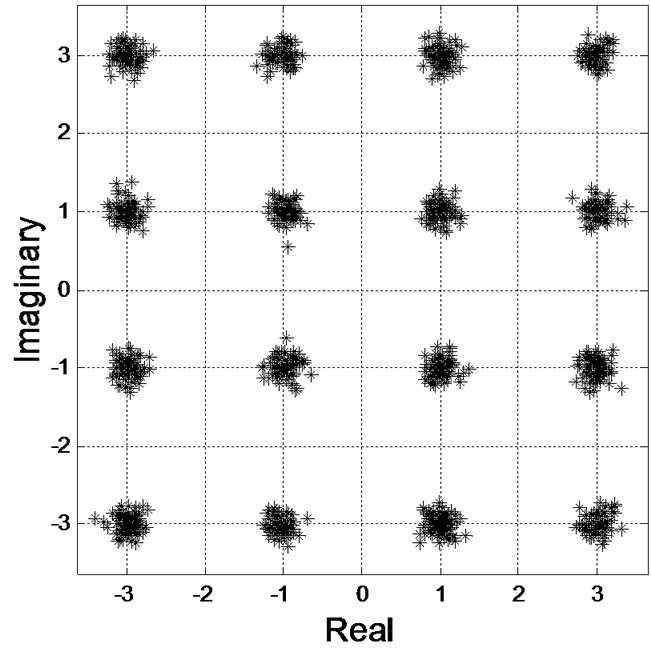 (f)
(f)
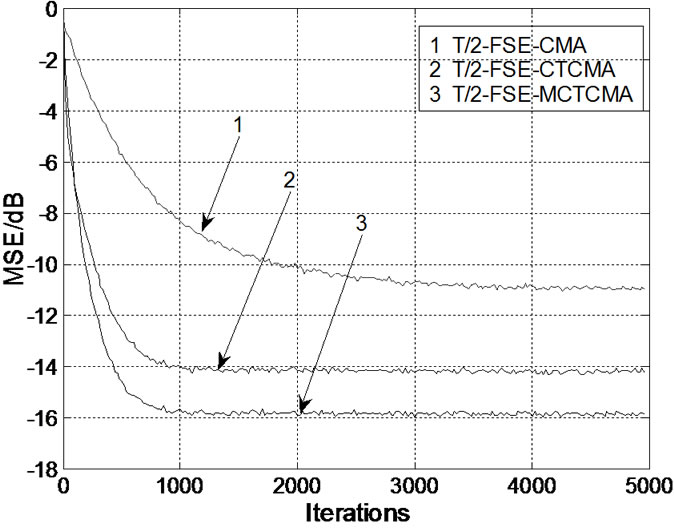
Figure 4. Simulation results. (a) Error curve; (b) Error curve of mean square root; (c) Input signals of equalizer; (d) Output signals of T/2-FSE-CMA; (e) Output signals of T/2-FSE-CTCMA; (f) Output signals of T/2-FSE-MCTCMA.
To 16 QAM signals, when the channel is equalized completely, Formula (9) is equal to zero. Until this, the T/2-FSE-MCTCMA is established. In this paper, we call the algorithm that the real and imaginary parts of input signal are not equalized, respectively, and only output signal is transformed as T/2 Fractionally Spaced blind Equalization algorithm based on Coordinate Transformation and CMA (T/2-FSE-CTCMA).
4. Performance Analysis
4.1. Convergence Performance Analysis
Input signal is sampled by the rate of 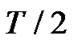 in T/2 fractionally spaced equalizer. It avoids spectrum aliasing by sub-sampling and compensates distortion of channel [19,20]. The real and imaginary parts of input signals in T/2 fractionally spaced equalizer are equalized, respectively, so it is equivalent to process real signal in the whole equalization process, and its computational complexity is decreased obviously. After the coordinate transformations of the real and imaginary parts of output signal are carried out, the mutli-modulus 16QAM signal is become constant modulus 4QAM signal. This treatment accelerates the updating speed of weight vector and when the channel is perfectly equalized, the error function tends to zero. So, the residual mean square error is decreased and the convergence rate is improved at end equalization.
in T/2 fractionally spaced equalizer. It avoids spectrum aliasing by sub-sampling and compensates distortion of channel [19,20]. The real and imaginary parts of input signals in T/2 fractionally spaced equalizer are equalized, respectively, so it is equivalent to process real signal in the whole equalization process, and its computational complexity is decreased obviously. After the coordinate transformations of the real and imaginary parts of output signal are carried out, the mutli-modulus 16QAM signal is become constant modulus 4QAM signal. This treatment accelerates the updating speed of weight vector and when the channel is perfectly equalized, the error function tends to zero. So, the residual mean square error is decreased and the convergence rate is improved at end equalization.
4.2. Analysis of Computational Complexity
In the T/2-FSE-CMA, each weight vector iteration needs 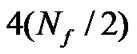 multiplications and
multiplications and  additions (
additions (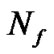 is the length of equalizer). However, in the T/2-FSE-MCTCMA, the computation load of real part of each weight vector iteration is
is the length of equalizer). However, in the T/2-FSE-MCTCMA, the computation load of real part of each weight vector iteration is  multiplications and
multiplications and  additions. So, the total computation load of each weight vector iteration is
additions. So, the total computation load of each weight vector iteration is  multiplications and
multiplications and 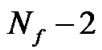 additions. Based on above analysis, the computation load of the T/2-FSE-MCTCMA has a drop of about a half comparison with that of the T/2-FSE-CMA.
additions. Based on above analysis, the computation load of the T/2-FSE-MCTCMA has a drop of about a half comparison with that of the T/2-FSE-CMA.
5. Simulation Results
In order to test the validity of the T/2-FSE-MCTCMA, we carried out simulation tests and compared the T/2-FSE-MCTCMA with the T/2-FSE-CTCMA and the T/2-FSE-CMA.
Simulation test 1: 16QAM signals were transmitted to mixed-phase water acoustic channel, the impulse response vector of this channel was given by 
 [21]; The SNR was set to 25 dB; the weight length of equalizer was set to 32; the weight length of each sub-channel equalizer was set to 16; the center tap of the weight vectors of all equalizer were initialized to one; the step sizes
[21]; The SNR was set to 25 dB; the weight length of equalizer was set to 32; the weight length of each sub-channel equalizer was set to 16; the center tap of the weight vectors of all equalizer were initialized to one; the step sizes ,
,  ,
,  were set to 0.000006, 0.00003, 0.0009, respectively. Simulation results of 5000 Monte-Carlo times were shown in Figure 4.
were set to 0.000006, 0.00003, 0.0009, respectively. Simulation results of 5000 Monte-Carlo times were shown in Figure 4.
Figure 4(a) shows that the MSE of the T/2-FSE-MCTCMA has a drop of about 2dB or 5dB comparison with that of the T/2-FSE-CTCMA or the T/2-FSE-CMA, respectively; the convergence rate of the T/2-FSEMCTCMA is the fastest in all algorithms and performs an improvement of about 2000 steps comparison with the T/2-FSE-CMA. Root mean square error of the T/2-FSEMCTCMA is minimum under the condition of the different SNR (see Figure 4(b)). The constellations of output signals in the T/2-FSE-MCTCMA is the clearest (see Figure 4(d), (e) and (f)). So, the T/2-FSE MCTCMA has great ability to suppress intersymbol interference.
Simulation Test 2: transfer function of the channel was given by
was given by 
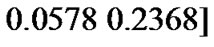 [21]. After 5000 signal points were transmitted, the channel
[21]. After 5000 signal points were transmitted, the channel  was changed into the channel
was changed into the channel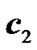 , its transfer function was given by
, its transfer function was given by 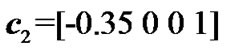 [21]. After 10000 signal points were transmitted, the channel
[21]. After 10000 signal points were transmitted, the channel  was changed into the channel
was changed into the channel , its transfer function was given by
, its transfer function was given by 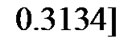
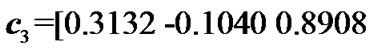 [21]. This established channel was called as time-varying channel.
[21]. This established channel was called as time-varying channel.
The transmitted signals were 16QAM signal; the SNR was set to 25 dB; the weight length of equalizer was set to 32; the weight length of each sub-channel equalizer was set to 16; the center tap of the weight vectors of all equalizer were initialized to one. In the time-varying channel, the step sizes of the three algorithms were shown in Table 1. Simulation results of 500 times Monte-Carlo were shown in Figure 5.
Figure 5(a) illustrates that the T/2-FSE-MCTCMA outperforms the T/2-FSE-CTCMA and T/2-FSE-CMA in equalizing the time-varying channel and has strong restarted ability and can rapidly track time-varying channel
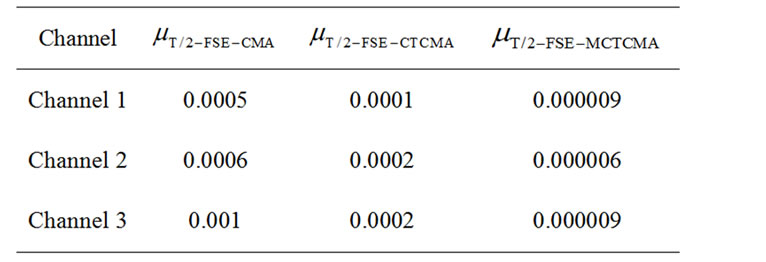
Table 1. The step size of three algorithms.
 (a)
(a) (b)
(b)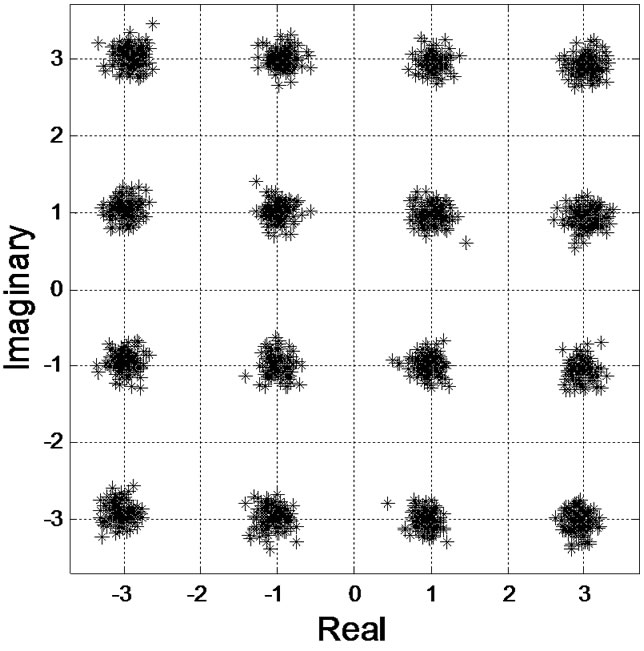 (c)
(c)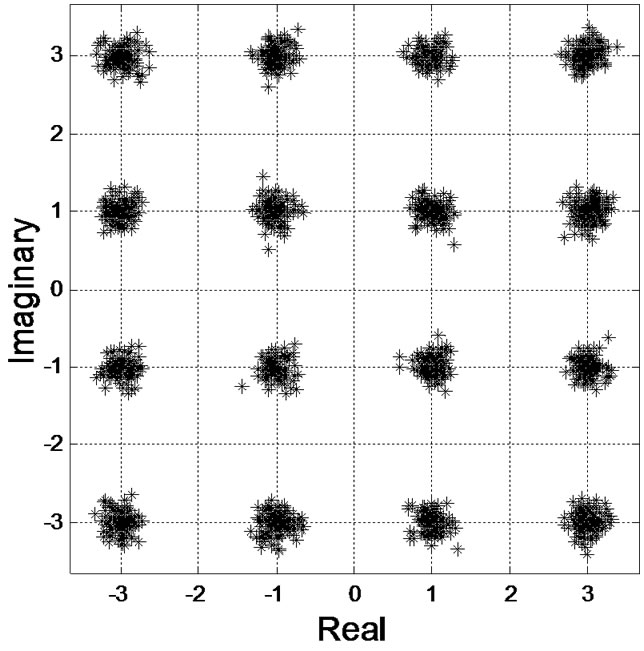 (d)
(d)
Figure 5. Simulation Results. (a) Error curve; (b) Output signals of T/2-FSE-CMA; (c) Output signals of T/2-FSE-CTCMA; (d) Output signals of T/2-FSE-MCTCMA.
and that the output constellations of the T/2-FSEMCTCMA are also the clearest.
6. Conclusions
In this paper, a Modified T/2 Fractionally Spaced blind Equalization algorithm based on Coordinate Transformation and CMA(T/2-FSE-MCTCMA) is proposed, its computation load has a drop of about a half comparison with that of the T/2-FSE-CMA(T/2 Fractionally Spaced blind Equalization algorithm based on CMA). For 16QAM signals, the equalization performance of the T/2-FSE-MCTCMA is optimal. Simulation results with the different underwater acoustic channels indicate that the T/2-FSE-MCTCMA has faster convergence speed, the lower MSE, and the clearest constellations comparison with the T/2-FSE-CTCMA(T/2 Fractionally Spaced blind Equalization algorithm based on Coordinate Transformation and CMA) and the T/2-FSE-CMA. So, the T/2-FSE-MCTCMA can effectively eliminate Intersymbol Interference(ISI) and recovery signals real-timely.
7. Acknowledgment
This paper is supported by Specialized Fund for the Author of National Excellent Doctoral Dissertation of China (200753), Natural Science Foundation of Higher Education Institution of Jiangsu Province (08KJB510010) and “the peak of six major talent” cultivate projects of Jiangsu Province(2008026), Natural Science Foundation of Jiangsu Province(BK2009410).
8. References
[1] A. Naveed, I. M. Qureshi and A Hussain, et al. “Blind equalization of communication channels for equal energy sources: Energy matching approach,” Electronics Letters, Vol. 42, No. 4, pp. 247–248, 2006.
[2] Z. J. Liu, H. S. Xu, J. L. Wang, and K. C. Yi, “A novel hybrid blind equalization algorithm,” Journal of Electronic and Information Technology, Vol. 81, No. 7, pp. 1606–1609, 2009.
[3] O. Dabeer and E. Masry, “Convergence analysis of the constant modulus algorithm,” IEEE Transactions on Information Theory, Vol. 49, No.6, pp. 1447–1464, 2003.
[4] G. C. Li, C. B. Luo, X. G. Yang and Y. H. Gong, “New convex combination strategy for the MMSE blind equalization algorithms,” Journal of Electronic Measurement and Instrument, Vol. 23, No. 1, pp. 37–41, 2009.
[5] Y. Wang and W. Guo, “Blind equalization of constant modulus based on Support Vector Regression,” Journal of Electronic Measurement and Instrument, Vol. 22, No. 3, pp. 15–19, 2008.
[6] J. Liu and L. Y. Dai, “New Blind Equalization Algorithm Based on Multi-mode Error Switch,” Journal of Data Acquisition and Processing, Vol. 19, No. 2, pp. 167–170, 2004.
[7] X. L. Li and X. D. Zhang, “A family of generalized constant modulus algorithms for blind equalization,” IEEE Trans on communications, Vol. 54, No. 11, pp. 1913– 1917, 2006.
[8] Y. P. Zhang and J. W. Zhao. “Blind equalization algorithms based on fractionally spaced underwater acoustic channels,” Acoustics and Electronics Engineering, Vol. 78, No. 2, pp. 21–23, 2005.
[9] L. Zhou, J. D. Li and G. H. Zhang. “Novel DWPW system based on fractionally spaced equalizers and the maximum likelihood algorithm,” Journal of Xidian University (Natural Science), Vol. 33, No. 4, pp. 509–513, 2006.
[10] Y. C. Guo and R. G. Lin, “Blind equalization algorithm based on T/4 fractionally spaced decision feedback equalizer,” Journal of Data Acquisition and Processing, Vol. 23, No. 3, pp. 284–287, 2008.
[11] K. S. Chen and C. Y. Chu, “A propagation study of the 28GHz LMDs system performance with M-QAM modulations under rain fading,” Progress In Electromagnetics Research, No. PIER 68, pp. 35–51, 2007.
[12] Y. P. Zhang, Y. C. Guo and J. Z. Liu, “Blind equalization algorithm suitable for 16QAM signals for carrier recovery of underwater acoustic channel,” Journal of System Simulation, Vol. 20, No.1, pp. 156–158, 2008.
[13] Y. Q. Zhang, P. Li and Z. R. Zhang, “Dual-mode blind equalization algorithm for multi-lever QAM modulation based on Sign-CMA,” Journal of China Institute of Communication, Vol. 25, No. 5, pp. 155–159, 2004.
[14] G. Q. Dou, J. Gao and P Wang, “A concurrent constant modulus algorithm and soft decision-directed algorithm for blind equalization,” Signal Processing, Vol. 23, No. 6, pp. 833–835, 2007.
[15] W Rao and Y. C. Guo, “A new constant modulus algorithm based on dual-step size,” International Symposium on Test Automation and Instrument, 2006.
[16] W. Rao, K. M. Yuan, Y. C. Guo and C. Yang, “A simple constant modulus algorithm for blind equalizer suitable for 16QAM signal,” International Conference on Signal Processing Proceedings, pp. 1963–1966, 2008.
[17] Y. C. Wang, Z. L. Chen and Z. T. Liu, “Direct blind fractional spaced equalization algorithm based on channel output decorrelation,” Journal of Data Acquisition and Processing, Vol. 20, No. 3, pp. 323–327, 2005.
[18] L. Zhou, J. d. Li and G. H. Zhang, “Novel DWPW system based on fractional spaced equalizers and the maximum likelihood algorithm”. Journal of XiDian University, Vol. 33, No. 4, pp. 509–513, 2006.
[19] Y. C. Guo, “Adaptive blind equalization techniques,” Hefei Industrial University Press, 2007.
[20] B. J. Kim and D. C. Cox, “Blind equalization for short burst wireless communications,” IEEE Trans. On Vehicular Technology, Vol. 49, No. 4, pp. 1235–1247, 2000.
[21] F. Wang, “Higher-order statistics based on the acoustic channel blind equalization theory and algorithm,” PhD thesis, Northwestern Industrial University, 2003.

