Journal of Water Resource and Protection
Vol.6 No.4(2014), Article ID:44282,10 pages DOI:10.4236/jwarp.2014.64035
The Effects of Surface Water Velocity on Hyporheic Interchange
Timothy Sickbert1,2, Eric W. Peterson2
1School of Geology, Noble Research Center, Oklahoma State University, Stillwater, USA
2Department of Geography-Geology, Illinois State University, Normal, USA
Email: ewpeter@ilstu.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 15 November 2013; revised 12 December 2013; accepted 11 January 2014
ABSTRACT
When evaluating hyporheic exchange in a flowing stream, it is inappropriate to directly compare stream stage with subsurface hydraulic head (h) to determine direction and magnitude of the gradient between the stream and the subsurface. In the case of moving water, it is invalid to ignore velocity and to assume that stage equals the net downward pressure on the streambed. The Bernoulli equation describes the distribution of energy within flowing fluids and implies that net pressure decreases as a function of velocity, i.e., the Venturi Effect, which sufficiently reduces the pressure on the streambed to create the appearance of a downward gradient when in fact the gradient may be upward with stream flow drawing water from the subsurface to the surface. A field study correlating the difference between subsurface head and stream stage in a low-gradient stream indicates that the effect is present and significant: shallow subsurface head increases less quickly than stage while deeper subsurface head increases more quickly. These results can substantially improve conceptual models and simulations of hyporheic flow.
Keywords:Hyporheic Zone; Bernoulli Equation; Venturi Effect; Geomorphology; Fluvial; Groundwater/Surface Water Interaction; Streamflow

1. Introduction
As the space within the beds and banks where ground water mixes with surface water, the hyporheic zone (HZ) is integral and essential to stream and riparian ecosystems. This space provides habitat [1] [2] and refuge from catastrophic events for aquatic insects [3] [4] ; maintains ecosystem stability [5] [6] by controlling stream metabolism [7] [8] and retaining and cycling nutrients [6] [9] [10] .
Hyporheic zone studies have succeeded in describing subsurface flow occurring at specific sites for limited ranges of time. These successes provide the foundation for understanding HZ processes, but efficiency requires that general descriptions apply to many sites over a broad range of conditions. Ultimately, science’s goals must be to identify the parameters that exert the greatest control over hyporheic flow, to provide reliable methods for quantifying these parameters, and to construct meaningfully accurate models of specific sites. The list of possibly important parameters is long and includes the entire suite of substrate characteristics (e.g. skins, grain size distributions, bed forms, and bed mobility), channel morphology, stream hydraulics, head gradients (vertical, horizontal, micro, macro, local, and regional), chemistry, temperature, and viscosity.
Over the past two decades, researchers have measured and modeled pressure variations driving hyporheic flow under a variety of conditions. Thibodeaux and Boyle [11] experimentally demonstrated and mathematically described small-scale bedforms creating sufficient variability in hydraulic head (h) to drive flow into and draw flow from the streambed. Elliott and Brooks [12] advanced this work by developing an analytical model of the distribution of subsurface h, flux (Q), and residence time under sinusoidally varying streambed surface h. Extending this theoretical work into the field, Storey et al. [13] measured and modeled hyporheic flow under stream channels along a step down from a riffle to a pool. Matos et al. [14] and Cardenas et al. [15] further developed this idea by demonstrating that pressure differences across upstream and downstream banks can drive flow. The sum of these works strongly establishes the role of stream features that affect pressure distributions driving hyporheic flow, but it does not explore the fundamental physics describing pressure distributions as a function of fluid flow. This work is one-step toward the goal of exploring stream hydraulics on hyporheic exchange.
To develop a general model that accurately describes and predicts processes in a wide variety of streams, the entire range of fluid dynamics that describe the flow must be explored. The Venturi Effect, an implication of Bernoulli’s equation describing the conservation of energy in fluid flow, stands out as an intuitively obvious principle that has nevertheless not been addressed in the literature.
Bernoulli’s equation implies that in an equilibrated steady-state system of standing water, total head—elevation plus the gravitational force on the overlying water—is uniform throughout the system. This holds true of systems where water stands above saturated porous media. In such a system, as the free surface of the standing water changes elevation, subsurface head changes accordingly. However, Bernoulli’s equation implies that when surface water flows at a sufficient rate, downward pressure at the bed will be less than the weight of the overlying water. Velocity-induced lower pressure at the bed would affect the magnitude—and possibly the direction—of flux between the flowing water and the subsurface. This effect would be measurable in the shallow subsurface of a flowing stream, manifesting itself as subsurface pressure increasing less than stream stage. In an extreme case, the system will show apparently paradoxical simultaneous gradients upward from the deeper subsurface toward the streambed and downward from the stream surface towards the shallow subsurface.
Assuming that no force is introduced or withdrawn from a system, the net energy of that system remains constant. To conserve energy, as the velocity (u) of a fluid increases along a streamline, its pressure (P) decreases. Bernoulli’s Equation describing the conservation of energy implies that P varies with velocity (Equation 1)
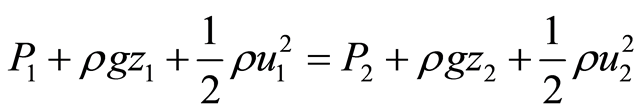 , (1)
, (1)
where P1 and P2 are the pressure at point 1 and point 2, respectively; u1 and u2 are the velocities, ρ is the density of the fluid, g is gravitational acceleration, and z1 and z2 are the elevations of the streamlines [16] . Comparing two points of equal elevation (z1 = z2) and setting u1 = 0 yields equation (2):
 , (2)
, (2)
which shows that pressure under flowing water is reduced below the pressure of standing water of the same depth by the kinetic energy of the flowing water.
To explore the effective magnitude of the Venturi Effect on hyporheic exchange, the paper reports on an in situ investigation into stream water velocity independent of bedforms as a control on head distributions in the shallow subsurface of a highly-permeable streambed. Specifically, the work examines the hypothesis that the difference in flow velocity between the point bar and the cut bank of a meander bend in a low-gradient stream is great enough to create a difference in pressure large enough to be measurable in the shallow subsurface. A difference sufficient to drive hyporheic flow should be measurable in the shallow subsurface. This research constrains the magnitude of this difference by measuring shallow subsurface pressure distributions for a range of velocities.
2. Geologic and Geohydrologic Setting of the Study Area
Data for this study were collected from Little Kickapoo Creek (LKC) adjacent to the Illinois State University Randolph Well Field, located in McLean County, central Illinois, USA (Figure 1). LKC is a low-gradient (0.001) third-order perennial stream. The stream heads about 11 km north of the study site, where its own and tributary channels have been modified. The drainage area upstream from the study site is about 52 km2 [17] . Locally, LKC is unmodified and meanders through an alluvial valley about 300 m wide [18] . Channel banks range from cut banks sharply incised through 2 to 2.75 m of the Holocene Cahokia Alluvium, to slumps and depositional point bars. The stream bed generally runs just below the top of 5 to 7 m of Wisconsinan Henry Formation glacial outwash. Riffles generally consist of gravel and coarse sand with minor interstitial silt. Point bars range from gravel to sand to mud. The local water table is relatively flat and very close to stream level. Results of pump tests at Illinois State University’s nearby well field indicate that the hydraulic conductivity of the Henry Formation is about 1 × 10−3 m/s.
The humid continental climate of the Midwest provides frequent showers and occasional heavy rain, especially during the spring and summer. Heavy precipitation events, urbanization in the headwater area, channelized upstream reaches, and ubiquitous agricultural field drain tiles all contribute to rapid, high-magnitude stream response.
3. Site Instrumentation and Data Collection Methods
The requirements for the study site include: 1) relative geomorphic stability over the period of the study; 2) a wide range of streamline flow velocities as the stage varies by up to a meter; and 3) accessibility for frequent manual stage measurements, water table elevations, and streamline velocities. The specific study site chosen based on these criteria is the apex of a meander bend in LKC (Figure 1) with relatively unobstructed flow, where average linear velocity and discharge vary from an extreme minimum 0.01 m/s and 0.003 m3/s at base flow after an extended dry period, to at least 0.80 m/s and 3.86 m3/s just below flood stage. The bed is unconsolidated silty, gravelly coarse sand from the cut bank to within 1 m of the point bar, which is uncompacted sandy mud underlain by coarser material. All stream bed material at the site is subject to erosion, and multiple episodes of scour lowering the stream bed by more than 0.3 m—and subsequent filling—were observed [19] . The episodes of scour temporarily exposed the shallow piezometer screens described below. The stream channel width ranges from about 3.7 m at low baseflow to 7 m at bankfull.
Four piezometer nests, LK1, LK2, LK2.5, and LK3, were installed in the stream channel. The nests are about 1.5 m apart, arranged perpendicular to the flow from the cut bank to the point bar, respectively (Figure 2). Each nest includes three piezometers aligned parallel to flow: A is furthest downstream with the top of the screen 1.6 m below the stream bed; B is upstream of A and screened 0.6 m below the stream bed; and C is furthest upstream and screened 0.1 m below the stream bed. All screen depths were measured relative to the stream bed at LK1 at the time the piezometers were installed. The piezometer screens are commercial 3.2 cm inside diameter steel drivepoints, with 3.2 cm galvanized steel pipe risers. The drivepoints’ screen open intervals are restricted with duct tape to 5 cm at the bottom of the Aand B-series drivepoints, and at the top of the C-series drivepoints. Stream stage and water table elevation in the piezometers were manually measured periodically with an electrical water-level tape to a resolution of 0.005 m. All stage and water table elevations are relative to an arbitrary local datum.
Stream velocity and stage were measured forty-five times, including duplicates and triplicates, on twenty-five days over the period from July 9 through November 29, 2003. Stream velocities were measured using an electromagnetic velocity meter. Velocities were measured at horizontal offsets along the stream transect directly upstream from each piezometer nest and at other arbitrarily-spaced points. Velocities measured directly upstream from the piezometers were used to test for a significant correlation between stream water velocity and piezometer water level. Other points not directly upstream from the piezometers were selected to adequately represent stream velocities and discharge based on flow patterns. Velocities varied from 0.0 m/s to 0.6 m/s within a meter of the cut bank, but would be nearly constant—stationary or slowly eddying—over a distance of 1.5 m approaching the point bar. Therefore, data density is higher adjacent to the cut bank than the point bar. At each ho-
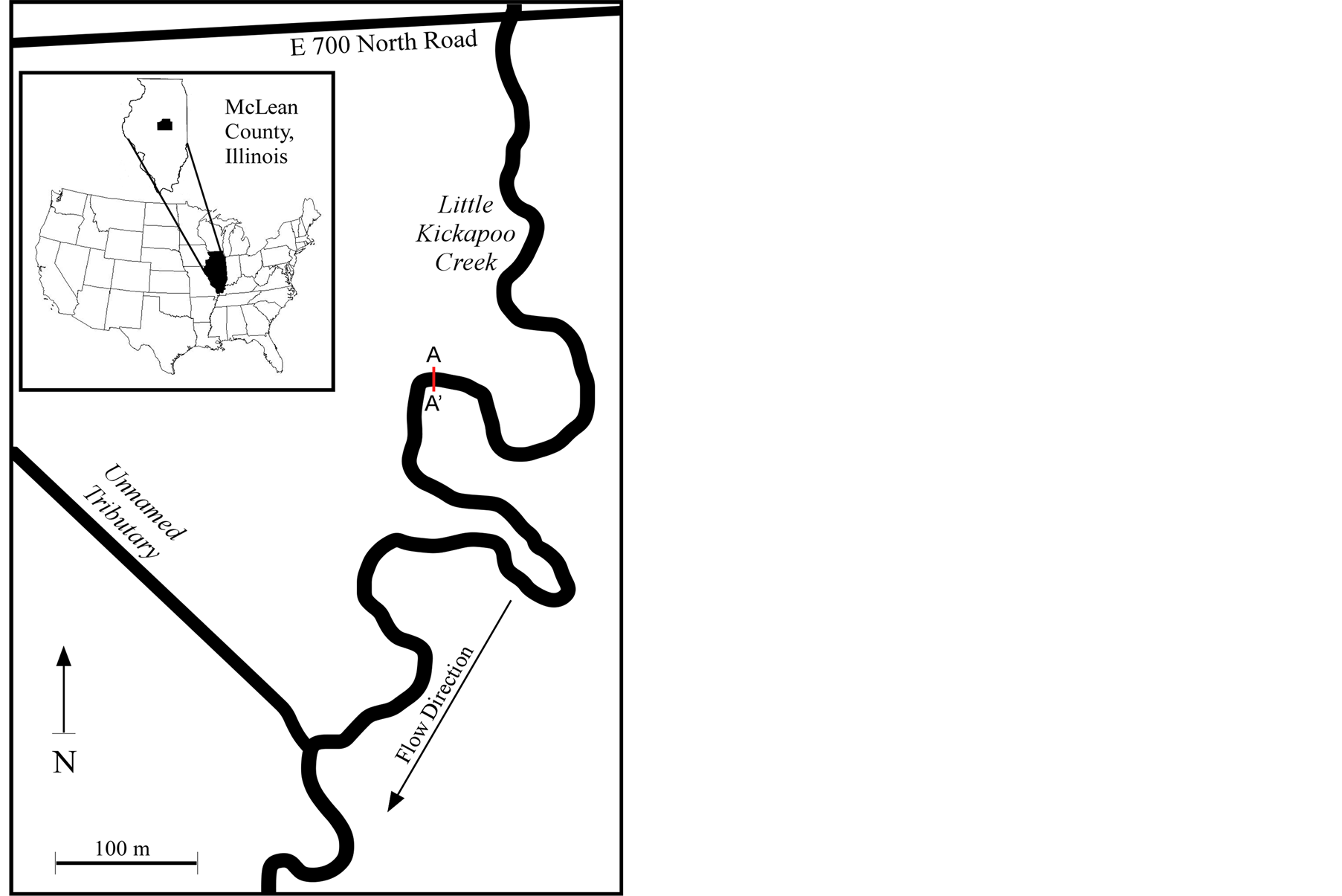
Figure 1. Study location-McLean County, central Illinois. Red line notes the location of cross-section A-A’ presented in Figure 2.
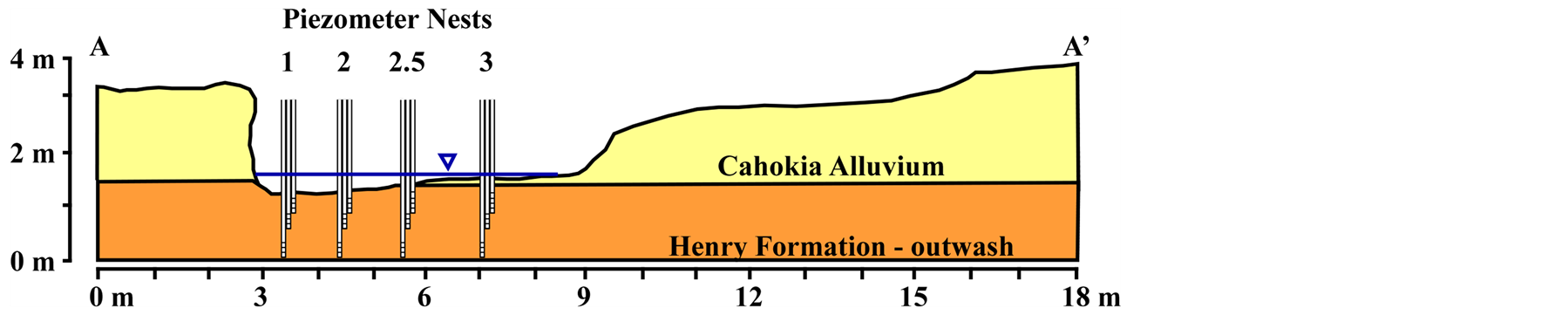
Figure 2. Lateral cross-section showing the arraignment of the piezometer nests. Crosssection is oriented such that stream would flow out of the figure.
rizontal offset along the transect, velocities were measured at multiples of 0.05 or 0.10 m below the stream surface, and at 0.03 m above the bed. Thus the stream cross-section is divided into a variable and arbitrary number of rectangular elements (Figure 3). Each element is bounded by the surface, bed, or bank as appropriate; otherwise by horizontal lines half the distance between depths at which velocities were measured, and by vertical lines half the distance between each horizontal offset. Stage was measured as the distance of the stream surface below the surveyed elevation of the tops of the piezometer pipes. Discharge for each element was calculated as the velocity (uij) measured at the center of the element xizj multiplied by its cross-sectional area (Figure 3). Total discharge was calculated as the sum of the discharge of the elements. Average linear velocity was calculated as the total discharge divided by the total cross-sectional area. Discharge ranged from 0.003 m3/s to 3.9 m3/s as stage varied by 1.3 m, and average linear velocity varied from 0.01 m/s to 0.80 m/s. Above about 0.75 m, stream flow conditions prevented reliable data collection.
4. Data
Data were collected as stage ranged up to 0.72 m above minimum stage, with two of these events (at 0.65 and

Figure 3. Schematic of velocity and discharge technique. Velocity was measured at points A, B, and C. Discharge for the element centered at B was calculated as QB = uB × xi × zj, where QB is the calculated discharge; uB is the velocity measured at point B; xi is the distance along the transect from half the distance to the previous offset to half the distance to the next offset; and zj, is the distance from half the distance to the previous depth to half the distance to the next depth.
0.72 m) above 0.36 m (Figure 4). These two higher-stage events are outliers that strongly influence statistical analysis without providing enough points to assure their significance; therefore, these events are omitted from the analysis although they appear to strongly support the conclusions. The remaining events provide sufficient data density and consistency for piezometers LK1, LK2, and LK2.5 for meaningful statistical analysis. Stream water velocity at piezometer LK3 was not measurable below 0.14 m above minimum stage and data up to 0.36 m are too few to support meaningful statistical analysis. Selected data from LK3 are included for illustration.
Velocity at LK1 near the cut bank varies little with stage relative to other measured streamlines, and stage predicts velocity moderately well (r2 = 0.65) (Figure 5). Velocities upstream of LK2 and LK2.5 increase much more rapidly and correlate more closely with stage (r2 = 0.85 and 0.86, respectively). The natural log regression lines show that water velocities increase much more quickly with distance from the cutbank and predict that the velocity at each piezometer should in turn become the highest. Velocity varies relatively little along the cut bank (LK1, red inverted triangles) and increases more rapidly (the slopes of LK2, blue circles half-filled on the left, and LK2.5, magenta circles half-filled on the right) and regularly (increasing values of r2) with distance from the cut bank.
5. Analysis and Discussion
Working from the assumption that stream water velocity has no effect on pressure in the shallow subsurface, a least-squares linear regression line of h plotted against stage should have a slope of unity. A slope significantly less than unity is evidence that flowing water reduces h in the shallow subsurface, i.e., the Venturi Effect. This is most meaningful for h in the shallowest C-level piezometers which, given their proximity and the high K of the substrate should closely match stream stage. Deeper piezometers are analyzed to more fully characterize the environment and to control for the possibility of larger-scale flow. The formal statistical test is:
 (3)
(3)
where m is the least-squares linear regression line slope calculated from observation and m0 is the null-hypothesis slope representing the condition of water velocity having no effect. The null-hypothesis slope is unity when plotting piezometer head values against stream stage. Least-squares linear regression line slopes are tested for statistically significant difference from a null-hypothesis slope of unity using the standard statistical test
 (4)
(4)
(Weiss, 1996) where t is the test statistic; se is the standard error of the slope; and Sxx is the standard error of

Figure 4. Piezometer head plotted against stage to 0.72 m, with least-squares linear regression lines.
the estimate. The test statistic t is evaluated against Student’s t-distribution for non-normal populations with (n − 2) degrees of freedom where n is the number of data points, giving p, the two-tailed probability of a slope at least as far from 1 as ma occurring by chance. For this study, any value of p less than 0.10 is considered to be significant evidence that ma ≠ 1. This statistical test uses the value of ma, the number of data points in the regression, and the variance of both the independent and the dependent variables. p is evaluated as a two-tailed probability to recognize slopes significantly greater and significantly less than one. Although the working hypothesis is only that the Venturi Effect will create slopes less than one, this analysis provides a more comprehensive picture. Evaluating two-tailed probabilities instead of one-tailed probabilities affects the analysis of only one instance, discussed below.
In this analysis, variances strongly affect the p-value. Consider for example regressions for LK1C and LK2A as functions of stage (Figure 6 and Table 1). Regression line slopes are very nearly equal (1.062 and 1.063, respectively) and LK1C has eighteen data points compared with eleven for LK2A. Nevertheless, the statistical test indicates a 0.17 probability of LK2A’s slope occurring by chance in contrast to LK1C’s 0.28 probability. The difference is in the standard errors of the estimates (sey) of the samples which are 0.025 for LK1C and 0.007 for

Figure 5. Water velocities (m/s) upstream of piezometers plotted against the natural log of the stage, with corresponding natural log regression lines and equations.

Figure 6. Piezometer water levels plotted against stage, with least-squares linear regression lines and equations for a) LK1, b) LK2, and c) LK2.5. Zero elevation is the lowest measured stream stage. In all plots, filled diamonds are from the deepest (a) piezometer at 1.6 m, hollow squares are from the intermediate-depth (b) piezometer at 0.6 m, and filled triangles are from the shallowest (c) piezometer at 0.1 m below the stream bed. All depths are measured relative to the stream bed at LK1.
LK2A. The low value for sey of LK2A makes the test result for difference of slope much more statistically significant.
Piezometer water levels are generally higher than stream stage, and LK1C increases most rapidly among the three LK1 piezometers. This may be an effect of stream water banking on the outside of the meander. No slope is statistically different from unity.
All piezometer water levels are higher than stream stage; LK2A increases more quickly than stage, but only marginally statistically significantly. LK2B and LK2C increase at rates statistically significantly less than stage, and LK2C at a rate much lower than LK2B.
Water-level in LK2.5A increases at essentially the same rate as stage and remains above stage (maintains an upward gradient). LK2.5B increases at a rate lower but not statistically significantly lower than stream stage, and remains above stage. LK2.5C increases at a rate statistically significantly lower than stream stage and apparently reverses the gradient as piezometer water level falls below stream stage. This suggests that the flowing
Table 1. Regression line parameters for Figure 6 where n is the number of data points, m is the slope of the least-squares regression line, b is the y-intercept (piezometer water level), r2 is the coefficient of determination, and p is the two-tailed probability of a slope at least as far from unity occurring by chance. Data lines with statistically significant values are bold.
water reduces downward pressure on the stream bed and draws water from the shallow subsurface.
The regression lines for all LK1 piezometers (Figure 6) have slopes statistically indistinguishable from unity. Although their slopes are distinctly different from unity, relatively high sey values for LK1A and LK1C—0.016 and 0.025, respectively—indicate that the variance within the data is too great to support statistically strong conclusions. LK1B has a low sey value of 0.004 but its slope of m = 0.993 is indistinguishable from unity. The very minor increase in velocity that accompanies the rise in stage may confound meaningful analysis of this limited dataset (note Figure 5). Head in the deeper two piezometers (LK1A and LK1B) remain above stage for the entire range, while head in the shallowest piezometer (LK1C) is generally closer to stage. The gradient among the depths is small but consistently upward, i.e., h increases with depth. The steeper slope of LK1C suggests that h in this piezometer will rise above h in the deeper piezometers, which may be an effect of water banking along the outside of the meander bend.
The water table elevation in the deepest (LK2A) piezometer increases at a rate higher but not statistically significantly different than the rate at which the stream stage increases (m = 1.063; n = 13, sey = 0.016; two-tailed t-distribution: p = 0.17). Note that a one-tailed test would give a statistically significant t-distribution p-value = 0.08 indicating that h deep within the streambed increases significantly faster than stream stage. This implies that the statistically significantly lower head in LK2B and LK2C, discussed below, occurs in the context of increased h in the deeper subsurface. Head in the intermediate LK2B piezometer increases at a rate significantly lower than stream stage (m = 0.951; n = 20; sey = 0.010; two-tailed t-distribution: p = 0.04). Head in the shallowest LK2C piezometer increases at a rate much lower than stream stage (m = 0.886; n = 21; sey = 0.011; two-tailed t-distribution: p < 0.001). Piezometer head remains higher than stream stage for the entire nest through stage of 0.36 m, although head in LK2C approaches stream stage at the high end of the range. The behavior of h in the shallowest piezometer warrants further examination. If stream water velocity is reducing downward pressure according to Bernoulli’s equation, and if all assumptions required by Bernoulli’s equation are valid, h should closely track theoretical net downward pressure as the height of the water column minus 0.5v2. Plotting LK2C h against the theoretical net downward pressure of the water column produces a leastsquares linear regression line with slope = 1.432 and a coefficient of determination r2 = 0.785. The coefficient of determination indicates that the stream stage minus the velocity component accounts for about seventy-nine percent of the change in piezometer head. A slope equal to unity would indicate that piezometer head tracks the theoretical Venturi Effect. The slope much higher than unity shows that any such velocity effect is significantly subdued. However, a plot of stage against (stage minus velocity component) would have a significantly higher slope of about 1.69. This difference suggests that piezometer head increases at a rate controlled in part by water velocity. Note that the plotted power regression curve is both more appropriate and provides a higher coefficient of determination for both datasets, but linear regression tracks the power regression very closely and provides a more comprehensible comparison. In the context of statistically significant increase in h greater than the increase in stage for LK2A, the LK2B and LK2C slopes lower than unity strongly indicate that flowing water reduces h in the streambed, even to the 0.50 m depth of LK2B.
Head in the deepest (LK2.5A) piezometer increases at a rate statistically indistinguishable from unity (m = 0.973; n = 21; sey = 0.017; two-tailed t-distribution, p = 0.491). Head in the intermediate (LK2.5B) piezometer increases at a rate that is lower but not statistically significantly lower than the rate at which the stream stage increases (m = 0.927; n = 17; sey = 0.024; two-tailed t-distribution, p = 0.249). Head in the shallowest (LK2.5C) piezometer increases at a rate that is substantially and statistically significantly lower than the rate at which the stream stage increases (m = 0.917; n = 24; sey = 0.004; two-tailed t-distribution, p < 0.0001). As with LK2C, the LK2.5C plot of piezometer h against the theoretical streambed pressure yields a slope much greater than unity (m = 1.422) but also significantly lower than the null hypothesis slope (m = 1.581), again supporting the alternate hypothesis that velocity affects subsurface head.
Note that subsurface h begins to fall below stream stage when stage reaches 0.17 m. This appears to suggest that water would flow from the stream into the subsurface. However, Bernoulli’s equation predicts this phenolmenon, i.e., as the velocity of the water flowing in the stream increases, the downward pressure exerted upon the streambed by the water in the stream declines as a function of the one-half the square of the velocity. This strongly supports the alternate hypothesis that water velocity reduces the shallow subsurface pressure. Contrary to the superficial appearance of a downward gradient, this data shows that the flowing stream water is drawing water from the subsurface.
6. Conclusions
Statistical analysis of measured h in the shallow subsurface of a streambed shows that h increases less than stage. This difference appears to correlate with the water’s increased velocity as stage rises. Shallow piezometer h rises faster than stage near a cut bank where velocity increases little. Where the velocity increase with stage is greater, shallow subsurface h increases less than stage. This occurs both where the gradient between the deeper subsurface and the stream increases (LK2) and where it decreases (LK2.5). The effect is great enough to apparently reverse the gradient from upward to downward. However, Bernoulli’s equation predicts the appearance of this effect. The lowered values of measured subsurface h in LK2C and LK2.5C result from the reduced downward pressure of the flowing stream water. In spite of the apparent downward gradient, subsurface hyporheic zone water continues to flow upward into the stream. This is also the “Bernoulli lift” that contributes to particle entrainment in, for example, Baker and Ritter [20] .
As researchers integrate into multidisciplinary environmental and ecological studies, it is important that they re-examine assumptions that are generally valid within more narrow disciplines. In ground water, for example, it is generally valid to assume that water table elevation within a piezometer pipe adequately represents total h. Stream surface elevation (stage), however, does not adequately represent stream total h: velocity becomes a significant component. When analyzing, comparing, and modeling HZ processes, it is not valid to directly compare stream surface elevation with shallow subsurface water table elevations. Such comparisons should include an accounting for the flowing stream water’s kinetic energy component as described by Bernoulli’s equation. The results presented here suggest that further investigations into the effects of substrate characteristics and the attenuation of the effect with depth are warranted.
Acknowledgements
The work was supported by student research grants awarded by the Geological Society of America, the Quarternary Geology and Geomorphology Section of the Geological Society of America and Sigma Xi to T.S. Acknowledgements are made to the Bloomington-Normal Water Reclamation District for their cooperation, and to Oklahoma State University for their material support.
References
- Stanford, J.A. and Ward, J.V. (1988) The Hyporheic Habitat of River Ecosystems. Nature (London), 335, 64-66. http://dx.doi.org/10.1038/335064a0
- Williams, D.D. (1984) The Hyporheic Zone as a Habitat for Aquatic Insects and Associated Arthropods. In: Resh, V.H. and Rosenberg, D.M., Eds., The Ecology of Aquatic Insects, Praeger Publishers, New York, 430-455.
- Dole-Olivier, M.-J., Marmonier, P. and Beffy, J.-L. (1997) Response of Invertebrates to Lotic Disturbance: Is the Hyporheic Zone a Patchy Refugium? Freshwater Biology, 37, 257-276. http://dx.doi.org/10.1046/j.1365-2427.1997.00140.x
- Schmid-Araya, J.M. (2000) Invertebrate Recolonization Patterns in the Hyporheic Zone of a Gravel Stream. Limnology and Oceanography, 45, 1000-1005. http://dx.doi.org/10.4319/lo.2000.45.4.1000
- Grimm, N.B., Valett, H.M., Stanley, E.H. and Fisher, S.G. (1991) Contribution of the Hyporheic Zone to the Stability of an Arid-Land Stream. Verhandlungen der Internationalen Vereinigung fur Theoretische und Angewandte Limnologie, 24, 1595-1599.
- Valett, H.M., Fisher, S.G., Grimm, N.B. and Camill, P. (1994) Vertical Hydrologic Exchange and Ecological Stability of a Desert Stream Ecosystem. Ecology, 75, 548-560. http://dx.doi.org/10.2307/1939557
- Grimm, N.B. and Fisher, S.G. (1984) Exchange between Interstitial and Surface Water: Implications for Stream Metabolism and Nutrient Cycling. Hydrobiologia, 111, 219-228. http://dx.doi.org/10.1007/BF00007202
- Mulholland, P.J., Marzolf, E.R., Webster, J.R., Hart, D.R. and Hendricks, S.P. (1997) Evidence That Hyporheic Zones Increase Heterotrophic Metabolism and Phosphorus Uptake in Forest Streams. Limnology and Oceanography, 42, 443-451. http://dx.doi.org/10.4319/lo.1997.42.3.0443
- Triska, F.J., Kennedy, V.C., Avanzino, R.J., Zellweger, G.W. and Bencala, K.E. (1989) Retention and Transport of Nutrients in a Third-Order Stream in Northwestern California: Hyporheic Processes. Ecology, 70, 1893-1905.
- Wondzell, S.M. and Swanson, F.J. (1996) Seasonal and Storm Dynamics of the Hyporheic Zone of a 4th-Order Mountain Stream, I: Hydrologic Processes. Journal of the North American Benthological Society, 15, 3-19.
- Thibodeaux, L.J. and Boyle, J.D. (1987) Bedform-Generated Convective Transport in Bottom Sediment. Nature (London), 325, 341-343. http://dx.doi.org/10.1038/325341a0
- Elliott, A.H. and Brooks, N.H. (1997) Transfer of Nonsorbing Solutes to a Streambed with Bedforms; Laboratory Experiments. Water Resources Research, 33, 137-151. http://dx.doi.org/10.1029/96WR02783
- Storey, R.G., Howard, K.W.F. and Williams, D.D. (2003) Factors Controlling Riffle-Scale Hyporheic Exchange Flows and Their Seasonal Changes in a Gaining Stream; A Three-Dimensional Groundwater Flow Model. Water Resources Research, 39, 1034. http://dx.doi.org/10.1029/2002WR001367
- Matos, J.E.R., Welty, C. and Packman, A.I. (2003) Stream-Groundwater Interactions: The Influence of Aquifer Heterogeniety and Stream Meandering on 2-D and 3-D Hyporheic Exchange Flows. Proceedings of MODFLOW and More 2003: Understanding through Modeling, Integrated Ground Water Modeling Center, Golden, 47-50.
- Cardenas, M.B., Wilson, J.L. and Zlotnik, V.A. (2004) Impact of Heterogeneity, Bed Forms, and Stream Curvature on Subchannel Hyporheic Exchange. Water Resources Research, 40, W08307. http://dx.doi.org/10.1029/2004WR003008
- Munson, B., Young, D. and Okiishi, T. (1998) Fundamentals of Fluid Mechanics. 3rd Edition, John Wiley & Sons, Inc., New York.
- Peterson, E.W. and Benning, C. (2013) Factors Influencing Nitrate Within a Low-Gradient Agricultural Stream. Environmental Earth Sciences, 68, 1233-1245. http://dx.doi.org/10.1007/s12665-012-1821-x
- Beach, V. and Peterson, E.W. (2013) Variation of Hyporheic Temperature Profiles in a Low Gradient Third-Order Agricultural Stream—A Statistical Approach. Open Journal of Modern Hydrology, 3, 55-66. http://dx.doi.org/10.4236/ojmh.2013.32008
- Peterson, E.W., Sickhert, T.B. and Moore, S.L. (2008) High Frequency Stream Bed Mobility of a Low-Gradient Agricultural Stream with Implications on the Hyporheic Zone. Hydrological Processes, 22, 4239-4248. http://dx.doi.org/10.1002/hyp.7031
- Baker, V.R. and Ritter, D.F. (1975) Competence of Rivers to Transport Coarse Bedload Material. Geological Society of America Bulletin, 86, 975. http://dx.doi.org/10.1130/0016-7606(1975)86<975:CORTTC>2.0.CO;2


