Journal of Service Science and Management
Vol.11 No.01(2018), Article ID:82724,26 pages
10.4236/jssm.2018.111011
Decision-Making in Dual-Channel Green Supply Chain Considering Market Structure
Yong-Mei Xu, Ping Zhang
School of Management, Jinan University, Guangzhou, China
Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: January 18, 2018; Accepted: February 25, 2018; Published: February 28, 2018
ABSTRACT
With the increasing awareness of environmental protection among consumers, green products are increasingly favored by the general public. The rapid development of e-commerce has increased the channels for consumers to contact and purchase green products. In this paper, consumers’ perceived differences in product greenness among different channels are considered and three models of manufacturer-dominated Stackelberg game, retailer-dominated Stackelberg game and Nash equilibrium with equal power are constructed based on the difference pricing between online and offline channels. Also, the results of dual-channel structure are compared with those of single-channel respectively. The results show that when the green R & D costs are relatively high, manufacturers and retailers are motivated to compete as channel leaders, but for the entire supply chain, Nash’s decision-making can improve product greenness and profitability of the supply chain. When green R & D costs are low, manufacturers’ profits are higher under asymmetric power supply chains and lowest under vertical Nash decisions. Under the three kinds of power structure, product greenness and manufacturer’s profit are higher than single channel under dual-channel structure. The comparison of retailer’s profit in dual channel and single channel depends on green R & D costs.
Keywords:
Green Supply Chain, Dual-Channel, Channel Structure, Differential Pricing

1. Introduction
In recent years, the rapid development of e-commerce has triggered a boom in online shopping for all people. In order to encourage the consumption of green products, the industrial green development plan (2016-2020) proposes to promote the development of green manufacturing + Internet and promote e-commerce business direct sales or entities Enterprises cooperate to operate green products and services, and encourage the use of internet to sell green products to meet the diversified green consumption needs of different subjects. According to the report of the National Bureau of Statistics, in the first half of 2017, the online retail sales of energy-efficient products in the air conditioning industry increased by more than 550% over the same period of last year1, indicating that consumer attitudes toward online purchasing of energy-efficient air-conditioning products are taking shape. In addition, vertical structure of traditional supply chain often has different power structure. Strong manufacturers such as Gree, Haier, Midea take the initiative relying on their own technology and brand ownership in the supply chain. However, more and more offline retailers are emerging in the current market, such as Wal-Mart, Carrefour, GOME, Suning, etc. They have become increasingly powerful for the strong market share. Leading brands such as Gree have also taken advantage of offline physical stores to counter the channel monopoly of large retailers such as GOME and Suning. As a whole, there are three different supply chains with different power structures, they are manufacturer-dominated, retailer-dominated, and neither side dominated.
1The data are from the survey report of China’s National Bureau of Statistics.
The opening of online channels will help to promote green products, but will it benefit the development and production of green products? How will the different market structure affect the manufacturer’s green decision-making and the profits of supply chain? Therefore, it is of practical significance to study the dual-channel green supply chain decision under different market structures. This article reviews the literature from three aspects: green products, green supply chain and dual channels.
2. Literature Review
In the aspect of green products, scholars mainly study the concept and index system of green products. Navinchandra (1990) put forward the concept of green product design for the first time, which is to increase the compatibility between products and environment without impairing the function and quality of products [1] . In order to conduct a comprehensive quantitative evaluation of the environmental friendliness and resource conservation brought by green products, some scholars have proposed the concept of “greenness”. According to Dangelico (2010), greenness refers to the degree to which products conserve raw materials and energy and the degree of pollution to the environment from the product life cycle (product design, product purchasing, product manufacturing, product use, product recycling, etc.) [2] . In the research of index system of green degree, domestic scholars also put forward different evaluation methods and index system. For example, Xiang (2001) analyzed that greenness of products should include three major characteristics: technological advancement, environmental coordination and economic rationality [3] . According to these three characteristics, he established a system based on product greenness evaluation index system. Tao (2005) applied Life Cycle Inventory Analysis (LCIA), combined with the fuzzy evaluation theory and the green attribute of the product, constructed the step of evaluating the green degree of the product and the fuzzy evaluation matrix, and analyzed the application of the evaluation method [4] . Zhang et al. (2008) put forward a dynamic comprehensive evaluation model based on the entropy weight method, which is suitable for weighing different advantages. He determined the weight of the index according to the degree of variation of each index value and overcomes the limitation of the lack of flexibility in the evaluation due to the fixed weights existing in the past green product evaluation process [5] .
As the green degree of products gets more and more attention from the consumers, the enterprises enhance the competitiveness of the enterprises by improving the green degree of the products. The process from the raw materials to the final finished products involves the whole supply chain. Therefore, it has become an important direction of academic research that considering the greenness in the entire supply chain. The predecessors mainly studied the power structure of green supply chain and the competition of green supply chain. In the area of power structure, Ghosh (2012) further analyzed the effects of the three channel structures of manufacturer-led, retailer-led and vertical Nash on their respective profit and decision variables based on the supply chain consisting of a single retailer and a single manufacturer, and compared the influence of retailer-manufacturer joint decision-making green degree and decentralized decision-making product greenness on supply chain profit and decision variable [6] . Later, he considered both centralized decision-making and decentralized decision-making, and validated the existence of dual marginal effects and coordinated cost-sharing benefits among members of the supply chain [7] . Based on this, Jiang Shi Ying (2015), a domestic scholar, added green marketing costs and green utility to study the impact of different power structures on product greenness, product prices and wholesale price [8] . In the competition of green supply chain, Yu et al. (2016) established a green supply chain game model consisting of two manufacturers with a different green level and a retailer under the background of the government providing green subsidies, and found that the Product greenness and the level of government subsidies can be balanced solution [9] . Li et al. (2016) established a two-channel competition green supply chain game model, manufacturers can sell products either through retailers or direct sales channels through online channels, studies have shown that when the cost of green manufacturing is above a certain threshold , The manufacturer will not open the direct sales channel. When the consumer’s loyalty to the retail channel and the green manufacturing cost satisfy certain relations, the dual-channel green supply chain exists [10] . They explored the issue of endogenous selection of channels in green supply chains, which is much more instructive than the previous study of dual choice of firms as a fait accompli, but they considered only the predominance of manufacturers. Jamali et al. (2017) established a two-channel competition model between green and non-green supply chains, and analyzed and compared the intensity of price competition between channels. The effect of greenness on demand on sales price, product greenness and the impact of supply chain members’ profits [11] .
In the field of power structure of dual-channel supply chains, Zhang et al. (2012) analyzed the impact of product substitutability and channel position on pricing decisions in an exclusive dual-channel supply chain under different market structures. Their results show that vertical Nash equilibrium can be balanced for supply chain members, and that the structure of balanced supply of suppliers and retailers is the best for the entire supply chain [12] . Lu and Liu (2013) studied the pricing game in a hybrid two-channel distribution system where both physical retailers and online retailers coexist, the results show that the performance of both suppliers and retailers is influenced by different market structures [13] . Shi et al. (2013) used the supplier Stackelberg, retailer Stackelberg and Nash game to construct a supply chain market structure model under uncertain demand. Studies show that only when the demand is linear rather than the expected elasticity, Companies can profit when they are in a dominant position [14] . Chen et al. (2015) studied the optimal pricing and channel selection strategies for handset manufacturers under different channel powers based on the game theory model when the two purchase channels of smart phone industry, bare metal [15] . Zhang et al. (2015) built the Stackelberg game dominated by manufacturers and retailers and the Nash game model with equal power based on the differences in the power of members in the dual-channel supply chain. The study found that both manufacturers and retailers are willing to give up power and would rather do Stackelberg game followers, and Nash game is always the game player’s strict best practices [16] . Li et al. (2017) also considered the influence of channel spillover and service negative spillover effects on the decision-making of the two-channel supply chain. The service level, wholesale price, retail price and dual-channel performance were compared under different channel forces. Under the influence of different channels, the changes of total supply chain performance, direct channel performance and traditional channel performance mainly depend on the service negative spillover coefficient and the potential market share of direct channels [17] .
Through the research on green products, green supply chain management and dual-channel supply chain, we find that previous researches on green products and green supply chain have been enriched. A large number of scholars have made great achievements in the evaluation system of green products. Beneficial exploration, more scholars have studied the competition between multiple manufacturers or multiple retailers in the green supply chain offline channels. More scholars on the status quo of dual-channel research are based on the differences between online and offline channels. A few scholars study dual-channel green supply chain decisions that consider the greenness of products such as Li (2016) [10] and Jamali (2017) [11] . They are highly instructive based on the premise that manufacturers are dominant and consistent in price both online and offline. In general, there are two shortages: 1) in the actual scenario, the power structure of different dual-channel supply chains is different. At present, some scholars have studied the dual-channel green supply chain with the dominant manufacturer, few scholars study the dominant position of retailers and the competition between the two sides under the dual-channel green supply chain and few scholars compare the three different power structures analysis; 2) Some scholars have considered the situation where manufacturers and retailers make unified pricing for online and offline channels. There are few scholars to investigate the differences between manufacturer and retailer for different pricing of green products in different channels.
On the one hand, this article takes into account the peculiar attributes of green products and consumers’ perception of the green degree of products (the degree of energy-saving and emission-reducing of green products and the degree of harm to the human body and the environment) between traditional offline retail stores and online shopping centers to study the impact of this phenomenon on the research and development and production of green products. On the other hand, this article considers that different manufacturers and retailers may be in different market structures and studies the influence of different market structures on R & D, production and marketing of green products.
3. The Model
This paper considers a two-channel green supply chain with one manufacturer and one retailer in the supply chain, manufacturers have an online direct sales channel, and retailers have offline channels. In order to protect the environment and enhance market competitiveness, manufacturers will invest a certain amount of green research and development costs to produce a green product. Consumers may select offline retail stores to purchase products according to their shopping preferences, or they may choose to purchase products through the online channels.
The notations used in this article are in Table 1.
For the sake of analysis, the following assumptions were made:
1) Market demand is a linear function of sales price and product greenness, and is negatively correlated with sales price and positively correlated with product greenness. According to the study of Li (2016) [10] , it is assumed that the market demand in offline and offline channels are positive, the demand functions are:
(3.1)
(3.2)
2) The production of green products will not change the manufacturer’s
Table 1. Decision variables and model parameters.
marginal cost of production. However, in order to increase the greenness of the products, the manufacturer will invest a certain amount of R & D costs, and the
relationship between R & D costs and product greenness is: Ghosh (2014) and Zhu (2016) research [7] [18] .
3) Consumers can perceive the greenness of their products more truthfully through tactile, audible and sales staff explanations through offline retail channels. Therefore, the products with the same greenness have a greater impact on consumers through the offline retail channels than online channel [10] , that is to see .
4) The influence of cross price elasticity of elasticity on demand is less than the impact of its own channel price on demand, that is .
5) To prevent retailers from purchasing goods from online sources, suppose that manufacturers’ wholesale prices of online retail channels are lower than the direct sales prices of online channels.
Through the above model description and basic assumptions, we can get the profit function of the manufacturer:
(3.3)
Retailer profit function:
(3.4)
To satisfy Hypothesis 1 and Hypothesis 5, the following conditions are available:
(3.5)
(3.6)
4. Model Solutions
4.1. Centralized Dual-Channel Green Supply Chain Model
In the centralized decision-making model, retailers and manufacturers aim to maximize the profitability of supply chain systems, together determine the retail price of products, product greenness. According to the profit function of manufacturers and retailers, we can get the profit function of the entire dual-channel supply chain:
(4.1)
In order to make the function have the optimal solution, construct the Hessian matrix:
.
if , , that is
, and then the function has the optimal solution.
For the total profit function in the supply chain, solving the partial derivative of a with respect to and , making it equal to 0, we get:
The above equations can be combined to obtain the optimal decision and the total profit:
; ; ; .
4.2. Manufacturer Stackelberg (MS) Model
Under the manufacturer-led dual-channel green supply chain model, manufacturers can sell green products through off-line channels and online channels. The game sequence of the model is that the manufacturer first determines the greenness of the green product , the wholesale price and the sales price of the online direct sales channel , and then the retailer decides the price of the green product of the offline channel .
Adopting the method of reverse induction, the derivative function of the retailer is first evaluated as derivative and a value of 0 is obtained.
Substituting the expression of into the manufacturer’s profit function, then deriving the partial derivative of the greenness, the wholesale price, and the online direct selling price, and making it 0.
Substituting the above formula into the profit function of the retailer yields the optimal offline retail price:
Substituting the above optimal solutions into the profit functions of manufacturers and retailers, respectively, we can obtain the profits of manufacturers and retailers:
.
4.3. Retailer Stackelberg (RS) Model
In the current market, more and more offline retailers, such as Wal-Mart, Carrefour, GOME and Suning, are emerging in the current market. Increasingly, because of their high market share, these retailers have more and more buyers to compete, creating the predominance of retailers (RS model). This section will analyze the Stackelberg game model dominated by retailers. The order of the game is: the retailer first determines the price of the green product under the offline channel , and then the manufacturer determines the greenness of the green product , the wholesale price and the online channel selling price .
Adopt the backward induction method to solve the model, so that , for the manufacturer’s profit function, we can find the partial derivative of , and , let them be 0 to get the corresponding expression. The simultaneous equations of the three equations can be obtained, Then replace them into the profit function of the retailer, we can find:
And then, we can obtain the value of , .
;
;
.
4.4. Vertical Nash (VN) Model
In addition to the domination of manufacturers and the predominance of retailers, the reality is that there is still a close match between the two sides. More and more large offline retailers, such as Wal-Mart, Carrefour, GOME and Suning, have emerged in the current market. Due to the high market share, the buyers owned by these retailers have more and more counterbalanced forces. In order to counter the channel monopoly of large retailers, leading brands such as Gree and Haier have set up offline physical stores and online shopping malls And flagship stores, they are in a close race between powerful retail channels, the Nash game (VN mode). As both manufacturers and retailers are evenly matched, both sides make the same decision, with the retailer deciding on the green price of the offline channel while making decisions about the greenness of the product , the wholesale price , and the sales price of the online direct sales channel .
Let , denote the retailer’s profit from the unit product. The retailer function finds partial derivatives of and makes it 0, we can obtain:
The manufacturer function finds partial derivatives of and makes them be equal to 0, the optimal solution of decision variables can be obtained for the simultaneous establishment of three equations:
Furthermore, we can find the profits of manufacturers, retailers and the entire supply chain: . Where .
4.5. The Results of Single-Channel
For a single green supply chain composed of one manufacturer and one retailer, scholars have done a lot of research, and the methods and conclusions of model building have been very mature. Therefore, this paper refers to adopt the Modeling method of Ghosh (2012) [6] , demand function and profit function are as follows:
(4.2)
(4.3)
(4.4)
Through the above solution, we can find the optimal equilibrium solution and profit under the domination of manufacturer, retailer-led and Nash respectively. The results are shown in Table 2.
5. Comparative Analysis of the Results under Different Power Structure
In this section, we conduct a comparative analysis of the equilibrium solutions, market demands and profits obtained under different power structures in the previous section. The purpose of this section is to explore the impact of different power structures on the decisions of the dual-channel green supply chain and the profits of the supply chain and the efficiency of the entire supply chain.
Proposition 5-1: Optimal product greenness under different power structures satisfy the following:
If , then ;
If , then ,
where .
The proof of Proposition 5-1 to Proposition 5-9 are shown in the Appendix.
Proposition 5-1 shows that the product greenness is the highest under centralized decision-making and the lowest in MS mode regardless of the high or low green development costs. This is because under the centralized decision-making, both parties aim at maximizing the profit of the entire supply chain and can
Table 2. Optimal decisions and profits of a single channel under different power structures.
maximize the greenness of their products. In the MS model, the manufacturer as a leader in the supply chain, on the one hand, it can get more profits by adjusting the online wholesale, on the other hand, because they would increase their product green costs to improve the product greenness, so Manufacturers do not have enough incentive to improve product greenness, which leads to the lowest green level in MS mode. The comparison of the green degree of products in VN mode and RS mode depends on the relationship between the green R & D cost coefficient, the impact coefficient of product greenness on demand and the price competition intensity.
Proposition 5-2: Optimal wholesale prices under different power structures satisfy the following:
If , then ; if , then ;
If , then , and if , then .
where ;
.
Proposition 5-2 shows that the wholesale prices under the three power structures are more affected by the green R & D costs. When the R & D cost coefficient is very low, the wholesale price under the RS mode is the highest, which is caused by the high greenness of the products under the RS mode. With the increase of R & D cost coefficient, the wholesale price of RS mode will decrease. Even when the R & D cost coefficient is higher than a certain threshold, the wholesale price under RS mode is the lowest. The main reason is that the retailer will reduce the wholesale price because of the dominant channel in RS mode. The trend of wholesale price in MS mode is contrary to RS mode, when the R & D cost coefficient is very low, the green degree of the product in MS mode is the lowest, resulting in the lowest wholesale price. With the increase of R & D cost coefficient, the wholesale price will increase in MS mode, and the wholesale price in MS mode is the highest even when the green R & D cost coefficient is higher than a certain threshold. This is because manufacturers tend to adopt a strategy of raising the wholesale price of their products as the green research and development costs increase, forcing the demand of offline channels to shift to online channels.
Proposition 5-3: Optimal online direct selling price under different power structures satisfy the following:
If , then ;
If , then .
It can be seen from Proposition 5-3 that the comparison of the direct selling prices under the different power structures is consistent with the change of the green degree of products. Regardless of how the green R & D cost coefficient changes, the direct selling price under centralized decision is the highest, and the direct selling price under MS mode is the lowest, because the green degree of products is the highest under centralized decision making. The lowest degree leads to the lowest direct selling price in MS mode. The comparison of online direct selling prices between VN mode and RS mode is affected by the green R & D cost coefficient.
Proposition 5-4: Optimal offline retail prices under different power structures satisfy the following:
If , then ;
If , then ;
If , then ;
where .
Proposition 5-4 shows that when R & D costs are low, the offline retail price is the highest among centralized decisions and lowest in MS mode. Due to the low R & D cost, there is a big difference between green decision making and decentralized decision making, resulting in large differences in production costs of green products. Although centralized decision-making can eliminate the influence of double marginal effects, it cannot offset the impact caused by large cost differences. Therefore, centralized decision-making has the highest retail price under the line and the lowest green degree in MS mode has also led to the offline retail sales lowest price when green research and development costs are high, the offline retail price is the highest in MS mode, followed by RS mode, then VN mode, and finally the centralized decision mode. This is because the cost is too high, the difference of green degree is less under centralized and decentralized decision, and the effect of eliminating double marginal effect is greater than that of cost difference. Therefore, the retail price under centralized decision is the lowest. When the manufacturer is dominant, the highest price wholesale led to the highest offline retail price.
Proposition 5-5: Demand for retail channels under different power structures satisfy the following:
If , then ;
If , then .
Proposition 5-5 shows that regardless of how the green R & D coefficient changes, the demand for offline retail channels is always the highest under centralized decision and is always the lowest in MS mode. For the whole supply chain, the green degree of products under the centralized decision leads to the greater demand of the offline channels. In MS mode, manufacturers inhibit the greenness of the product and reduce the demand for the entire offline channel to a minimum, because they take the dominant position in the supply chain. The comparison between offline demand in RS mode and VN mode is affected by the size of R & D cost factor.
Proposition 5-6: Online demand under different power structures satisfy the following:
If 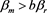 and
and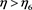 , then
, then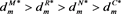 ,
,
If , then
, then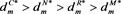 ;
;
If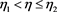 , then
, then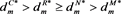 ,
,
where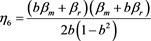 .
.
From Proposition 5-6 we can see that when the R & D cost coefficient is relatively low (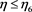 ), the online channel demand under different power structure is consistent with the offline demand, the demand of online channel is always the highest under centralized decision, the demand of online channel is always the lowest under MS mode. The comparison of offline demand under RS mode and VN mode is affected by the size of R & D cost coefficient, which shows that when the green R & D cost coefficient is low, there are no channel conflicts between the online channel and the offline channels. When the coefficient of green research and development cost increases (
), the online channel demand under different power structure is consistent with the offline demand, the demand of online channel is always the highest under centralized decision, the demand of online channel is always the lowest under MS mode. The comparison of offline demand under RS mode and VN mode is affected by the size of R & D cost coefficient, which shows that when the green R & D cost coefficient is low, there are no channel conflicts between the online channel and the offline channels. When the coefficient of green research and development cost increases (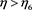 ), as manufacturers gain more profit per unit than online, the manufacturer shifts the offline demand to online by adjusting the greenness of the product and the size of the online selling price when the manufacturer dominates in the green supply chain, Resulting in the highest demand for online channels in MS mode and the lowest in centralized decisions. Therefore, there will be channel conflicts when the green R & D costs are large.
), as manufacturers gain more profit per unit than online, the manufacturer shifts the offline demand to online by adjusting the greenness of the product and the size of the online selling price when the manufacturer dominates in the green supply chain, Resulting in the highest demand for online channels in MS mode and the lowest in centralized decisions. Therefore, there will be channel conflicts when the green R & D costs are large.
Proposition 5-7: Manufacturers’ profit under different power structures satisfy the following:
If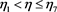 , then
, then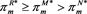 ; if
; if , then
, then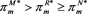 ; if
; if
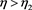 , then
, then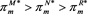 , where
, where
Propositions 5-7 shows that the comparison of manufacturer profits under different power structures is affected by the green R & D cost coefficient. When the R & D cost coefficient is high, the manufacturer’s profit is the highest in MS mode, followed by Nash’s decision, and lowest in RS mode. This is because manufacturers take the lead in the supply chain and have first mover advantage, they can adjust their decisions according to the retailers’ decisions. Therefore, the manufacturer has the highest profit under the dominant circumstances. In the RS mode, manufacturers can only adjust their decisions based on the offline channel prices set by the retailer, so profit is the lowest, manufacturer and retailer are more of a competitive relationship this moment. When the R & D cost coefficient is low, we can find that the tilt of power structure is more conducive to supply chain node enterprises. When supply and demand are evenly matched, it is unfavorable for both parties, which is consistent with the study by Zhang Guoxing et al. (2015).
Proposition 5-8: Retailer Profit under Different Power Structure satisfy the following:
Propositions 5-8 shows that retailer’s profit is only affected by the power structure, not influenced by the green R & D cost coefficient, which is highest in RS mode followed by VN mode and lowest in MS mode. In RS mode, retailers have the dominance of the supply chain, so it can gain more profit by controlling the selling price of offline channels. In MS mode, manufacturers seize the retailer’s value by adjusting the wholesale price and product greenness, retailer’s profit is the lowest at this time.
Proposition 5-9: The profit of the entire supply chain under different power structures satisfies the following:
If

If

Proposition 5-9 shows that regardless of changes in the cost of green research and development costs, the entire supply chain profits are the highest under the centralized decision-making, MS mode is the lowest. The main reason is that centralized decision eliminates the negative effects brought by the double marginal effect, improves the greenness of products and increases the demand of dual channels, resulting in the largest profit. In the MS model, manufacturers dominate the supply chain, on the one hand, they do not have enough power to improve the greenness of their products, so the demand is reduced. On the other hand, they control the online direct selling price and the offline wholesale price to transfer offline demand and grab the retailers’ profits, leading to a decline in the efficiency of the entire supply chain. The comparison of the profit of the whole supply chain between VN mode and RS mode depends on the size of the green R & D cost coefficient. When the R & D cost coefficient is low, supply chain node enterprises are more in a cooperative mode. As consumers’ perception of product greenness in online channels is better than that in offline channels, RS mode can further promote the demand for offline channels, resulting in a higher profit in RS mode. When the green R & D cost coefficient becomes larger, the supply chain enterprises are more competitive. The tilt of the power structure is not conducive to improving the efficiency of the entire supply chain. At this time, both sides can evenly reduce the competition and improve the efficiency of the entire supply chain.
6. Numerical Experiments
6.1. A Comparative Study of Different Power Structures
In order to intuitively indicate the size relationship between the online and offline demand under different power structure and the supply chain node enterprise profit, we make a two-dimensional map.
From Figure 1, we can see that when the manufacturer is dominant, the demand for offline is the lowest and the highest is for centralized decision. The relationship between retailer’s dominant and Nash’s decision size depends on the
Figure 1. Demand relationship under different power structure.
green R & D cost coefficient. When the green R & D cost coefficient is low, the offline demand is higher in RS mode, when the green R & D cost is higher, the offline demand is higher in VN mode. For the online market demand, as shown in Figure 1, when the green R & D cost coefficient is low, changes in online demand and offline demand are consistent. When the green R & D cost coefficient is larger, the manufacturer has the highest online demand when the manufacturer is in the dominant position. This shows that the dominant manufacturer will maximize the online demand at this time, we can also see that the demand for centralized decision-making is the lowest at this moment, which shows that the increase of green research and development cost will force manufacturers to take actions that are not good for the whole supply chain efficiency.
From Figure 2, we can see that when the green R & D costs are low, the
Figure 2. Profit relations under different power structures.
supply structure with tilted power is better than the situation that competing with each other, when green R & D costs are high, their profits diminish with the loss of manufacturer rights. For the entire supply chain profit, as shown in Figure 2, when the manufacturer is dominant, it does not benefit the efficiency of the whole supply chain. When R & D costs are low, the profits of the whole supply chain are the highest when the retailers dominate the decentralized decision-making, when the R & D costs of green increase, the profits of the entire supply chain will be more beneficial to both parties.
6.2. Single-Channel and Dual-Channel Comparative Analysis
This section examines the differences and changes in product greenness, selling prices, and profits for both manufacturers and retailers in a single-channel and dual-channel model under different power structures. In this paper, a case study is used to construct a three-dimensional map of decision variables and profits about green R & D costs and consumer preferences. Since the analysis under the retailer-led and Nash-based analyzes is consistent with the manufacturer’s dominance, only the manufacturer’s dominance is demonstrated here. The related parameters are assumed to be








From Figure 3, we can see that under certain conditions, regardless of the changes of 



Figure 3. Effect of 

Figure 4. Effect of 

Figure 5. Effect of 

Figure 6. Effect of 

preferences for online channels increase. Therefore, for manufacturers, the sooner the online sales are conducted, the less susceptible they are to traditional retailers. Consumers’ online shopping habits are a gradual process and taking into account that e-commerce has become a long-term development trend, the earlier opening of e-channels by manufacturers not only complies with this trend but also gives retailers more time to adapt to changes in the competitive environment, which is conducive to the healthy development of the supply chain.
6.3. Recommendations of the Comparative Analysis
We can get some management enlightenment from the comparative analysis of the above two parts. First, the manufacturers are inspired by the fact that they need to adopt different pricing strategies based on the cost of green research and development. When R & D costs are high, blindly squeezing supply chain partners with their own market power is a kind of “short-sighted” behavior and cannot achieve a win-win outcome. For the long-term development of the market, supply chain members should reach a consensus to support each other, rather than excessive pursuit of a dominance. Second, the conclusion of this paper shows that the channel conflicts between supply and demand sides are affected by the green R & D costs as well as consumer channel preferences. To avoid the channel conflict caused by opening online channels, manufacturers should reduce the green research and development costs as much as possible while the countries green subsidies should be provided to relieve manufacturers’ R & D cost pressures. With the rapid development of e-commerce, consumer preferences for online channels will be enhanced. Manufacturers should open online direct sales channels as soon as possible to reduce channel conflicts.
7. Conclusions
This paper considers consumer perceptions of greenness of different channel products, builds a dual-channel green supply chain game model with different power structures, analyzes the influence of related parameters on supply chain nodes and profits, and separately compares them with single channel. The main conclusions are as follows:
First, the optimal decision under different power structures is affected by the green R & D cost coefficient. When the green R & D costs are high, both manufacturers and retailers have the incentive to compete as leaders in dual-channel supply chains. However, for the entire supply, the profits of the entire supply chain under Nash’s decision are the highest. As manufacturers and retailers are in a fully competitive market, both the supply chain resource allocation and coordination efficiency are higher than that of the manufacturer-led and retailer-led; When the green R & D costs are lower, the profits of manufacturers are higher when the power supply structure of the supply chain is inclined, and are the lowest when both sides are evenly matched.
Second, a comparative analysis of enterprise profit and single channel of supply chain under three different power structures shows that, regardless of manufacturer-led, retailer-led and Nash-based decision-making, manufacturer profit and product greenness are better than single channel. Retailer profit in a single channel and dual channel influenced by green research and development costs and consumer channel preferences together, when the low cost of green research and development, consumers have a higher preference for offline channels, retailers’ profit will be higher in the dual channel. On the contrary, when the green R & D costs are higher and consumers’ preference for offline channels is weakened, the opening of online channels by manufacturers will reduce the profits of retailers and lead to double-channel conflicts. This is also different from the result of Li’s (2016) research. Based on the premise that retailers have the pricing power of online channels and offline channels, Li shows that with the increase of consumer preferences for offline channels, the profitability of the manufacturer will be reduced in dual-channel model or even lower than a single channel, retailers profit is always higher under a single channel. This article is based on the premise of online and offline differential pricing, leading to the conclusion of the difference. Once the manufacturer owns the autonomous pricing power of the online channel, the manufacturer can change the online and offline demand by adjusting the direct online selling price, thus affecting the profit structure of the supply chain.
The shortcomings of this paper are as follows: 1) For the dual-channel model of green supply chain, this paper considers only the manufacturers have the option of online and offline channels. Subsequent studies may further consider retailers’ options to own online channels, as well as consider the all-channel situation where manufacturers have both online and offline channels and retailers also have online and offline channels; 2) The demand function in this paper is a simple linear function. Considering the channel preference of consumers, Subsequent studies can use the uniform distribution function to establish the relevant model to conduct research.
Cite this paper
Xu, Y.-M. and Zhang, P. (2018) Decision-Making in Dual-Channel Green Supply Chain Considering Market Structure. Journal of Service Science and Management, 11, 116-141. https://doi.org/10.4236/jssm.2018.111011
References
- 1. Navinchandra, D. (1990) Steps toward Environmentally Compatible Product and Process Design: A Case for Green Engineering. The Robotics Institute, School of Computer Science, Carnegie Mellon University, Pittsburgh, PA.
- 2. Dangelico, R.M. and Pontrandolfo, P. (2010) From Green Product Definitions and Classifications to the Green Option Matrix. Journal of Cleaner Production, 18, 1608-1628. https://doi.org/10.1016/j.jclepro.2010.07.007
- 3. Xiang, D., Duan, G.H., Wang, J.S., et al. (2001) Integrated Assessment of Product Green Degree Based on Product System. Computer Integrated Manufacturing Systems, 8, 12-16.
- 4. Tao, J.H., Wang, J.F. and Zhang, R. (2005) Evaluation Method and Application of Product’s Green Degree Based on LCIA. Soft Science, 3, 10-13.
- 5. Zhang, Q.S., Xu, W., Qiao, F.L., et al. (2008) Manufacturers’ Green Product Choice Optimization Based on Entropy Method Industry. Management Review, 10, 45-50.
- 6. Ghosh, D. and Shah, J. (2012) A Comparative Analysis of Greening Policies across Supply Chain Structures. International Journal of Production Economics, 135, 568-583. https://doi.org/10.1016/j.ijpe.2011.05.027
- 7. Ghosh, D. and Shah, J. (2014) Supply Chain Analysis under Green Sensitive Consumer Demand and Cost Sharing Contract. International Journal of Production Economics, 164, 319-329. https://doi.org/10.1016/j.ijpe.2014.11.005
- 8. Jiang, S.Y. and Li, S.C. (2015) Green Supply Chain Game Models and Revenue Sharing Contract with product Green Degree. Chinese Journal of Management Science, 23, 169-176.
- 9. Yu, Y., Han, X. and Hu, G. (2016) Optimal Production for Manufacturers Considering Consumer Environmental Awareness and Green Subsidies. International Journal of Production Economics, 182, 397-408. https://doi.org/10.1016/j.ijpe.2016.09.014
- 10. Li, B., Zhu, M., Jiang, Y., et al. (2016) Pricing Policies of a Competitive Dual-Channel Green Supply Chain. Journal of Cleaner Production, 112, 2029-2042. https://doi.org/10.1016/j.jclepro.2015.05.017
- 11. Jamali, M.B. and Rasti-Barzoki, M. (2017) A Game Theoretic Approach for Green and Non-Green Product Pricing in Chain-To-Chain Competitive Sustainable and Regular Dual-Channel Supply Chains. Journal of Cleaner Production, 170, 1029-1043.
- 12. Zhang, R., Liu, B. and Wang, W. (2012) Pricing Decisions in a Dual Channels System with Different Power Structures. Economic Modelling, 29, 523-533. https://doi.org/10.1016/j.econmod.2011.08.024
- 13. Lu, Q. and Liu, N. (2013) Pricing Games of Mixed Conventional and E-Commerce Distribution Channels. Computers & Industrial Engineering, 64, 122-132. https://doi.org/10.1016/j.cie.2012.09.018
- 14. Shi, R., Zhang, J. and Ru, J. (2013) Impacts of Power Structure on Supply Chains with Uncertain Demand. Production & Operations Management, 22, 1232-1249. https://doi.org/10.1111/poms.12002
- 15. Chen, X. and Wang, X. (2015) Free or Bundled: Channel Selection Decisions under Different Power Structures. Omega, 53, 11-20. https://doi.org/10.1016/j.omega.2014.11.008
- 16. Zhang, G.X., Fang, S. and Wang, Y.L. (2015) Game Analysis in a Dual-channel Supply Chain with Different Power Structure. Systems Engineering, 3, 52-59.
- 17. Li, W., Li, K. and An, G. (2017) Decisions of Dual Channel Supply Chain when Considering Channel Power and Service Negative Spillover Effect. Chinese Journal of Management, 5, 767-774.
- 18. Zhu, W. and He, Y. (2016) Green Product Design in Supply Chains under Competition. European Journal of Operational Research, 258, 165-180.
Appendix
Proof of Proposition 5-1:
Because we must ensure the offline channel demand under centralized decision-making is positive, we obtain






Because

let

We can obtain
If

If

That is to see,
If

If

Proof of Proposition 5-2:



If

If

Let

If

If

Let


If

If

If

In summary, we can get:
If

If

If

If

Proof of Proposition 5-3:


So,
If

If

That is to see,
If

If

Proof of Proposition 5-4:
Let

If

If


If

If


If

If


If

If


Because
If 


If

In summary, we can obtain:
If

If

If

Proof of Proposition 5-5:





If

If

So we can obtain:
If

If

Proof of Proposition 5-6:
Let


If

If


If

If


If

If


If

If


If

If


If

Also, we can obtain:
If 


If

In summary, we can obtain:
If 


If

If

Proof of Proposition 5-7:
Let

If

If


Because


If

if

Because
If

If

If

Proof of Proposition 5-8:
Because


Proof of Proposition 5-9:
Because


so




If

If

In summary, we can obtain:
If

If














