Journal of Service Science and Management
Vol.08 No.02(2015), Article ID:55922,8 pages
10.4236/jssm.2015.82028
The Power of DOE: How to Increase Experimental Design Success and Avoid Pitfalls
Bruno G. Rüttimann1, Konrad Wegener2
1Inspire AG/ETH Zürich, Zürich, Switzerland
2IWF/ETH Zürich, Zürich, Switzerland
Email: bruno.ruettimann@inspire.ethz.ch
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 March 2015; accepted 20 April 2015; published 24 April 2015
ABSTRACT
Personal empirical experience when lecturing and consulting shows that not only students, but also experienced engineers familiar with DOE, show much more interest in the modeling of a process than to statistical inference, neglecting attention to “boundary conditions” of the process. But exactly the observation of ancillary boundary conditions of experiments, such as minimizing Beta-risk and noise, is determinant for the efficient execution of an experimental design and the effective application of DOE derived models. This essay focuses attention to the must-dos in the DOE statistics approach in order to avoid research pitfalls by presenting a fail-proof 14-step approach when applying DOE modeling.
Keywords:
Design of Experiments, Inference, Power, Beta Risk, Noise, Approach, Algorithm

1. Introduction
Design of experiments (DOE) is a structured, statistics based, active regression modeling which aims to optimize a response variable with regard to different input factors with a minimum number of trials. The word “power” in the title of this essay has a twofold meaning:
・ First, it points to the superiority of the DOE technique compared with one-factor-at-time (OFAT) or even with more simplistic Trial and Error (T&E) methods usually applied in industry, and
・ Second, it alludes to the statistics theory of being able to detect an effect discrimination between different realizations of a process input variable.
We will focus in this paper especially on this second aspect of the word power. Power (1 − β) is the complementary aspect of the Beta-risk in statistics inference. Compared with the Alpha-risk to make a type one error, the Beta-risk refers to the possibility to make a type two error. The attention in statistics inference is put on the Alpha-risk whereas the Beta-risk is usually neglected. This might be of secondary importance in industry, where even simplistic approaches, such as T&E, are widely applied in the belief of finding the “optimal” operating settings of production equipment. But on the contrary to industry, the Beta-risk cannot be neglected in scientific research to find a statistical significant effect. The aim of this paper is not to explain the theory of DOE modeling but to drive attention to Beta-risk and some additional aspects to be observed during the planning phase of scientific DOE to avoid potential pitfalls. In the following, we will at first briefly explain how DOE works, then we will enter into the reasons why the Beta-risk cannot be neglected, and in accordance, we propose a consistent 14-step DOE approach to avoid pitfalls in research, and finally a short algorithm to choose the proper DOE modeling; all this is aimed at students and researchers less familiar with statistics.
2. What Is DOE
Let us say, we have the assigned task in an industrial environment to find out the appropriate parameter settings of a machining equipment (e.g. type of cutting tool, cutting angle, mandrel revolutions, mandrel advancement) which optimizes the targets of surface roughness (quality) and oil consumption (efficiency). The task is to find the optimal settings of the independent variables such as cutting angle, mandrel revolution, and mandrel advancement optimizing both targets at the same time. This corresponds to a multi-objective function of which final settings should comply to Pareto-optimality. We can solve this problem with a black box approach, i.e. analyzing the phenotypic behavior of a system with an input-output transfer function even without knowing the mechano-thermodynamic physics law of cutting and heat dissipation. In a nutshell, we want to identify which factors have a statistical significant influence on the response, i.e. which terms are relevant to be retained in the final model. Compared to the OFAT approach, which suits the human brain capability, by varying only one factor at time to understand the response, the computer assisted DOE approach allows the variation of all settings simultaneously in order to find the response surface of the design space.
The most used DOE approach is a 2-level factorial design of experiments, either full, i.e. executing all, or fractional factorial, i.e. executing only a part of the trials of the design cube, leading to a linear model. The factorial design technique is to explore the hyperspace response surface of the corners of a k-dimensional design cube, eventually with placing in addition a center point to test for non-linearity of the response function (Figure 1). The number of experimental runs, also called trials, in one replicate is given by the fractional factorial notation
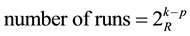
where 2 is the factor levels (low, high settings), k is the number of factors to be investigated, p is the partition called fraction of the whole experiment, and R is the resolution type, i.e. the confounding, in the case of a fractional design. For further details see e.g. [1] or another textbook on DOE.
Now, the statistical relevance of a factor for the model depends on the magnitude of the response to the change of the factor level, i.e. the effect (Figure 2) [2] . Virtually seen, the statistical significance is given by comparing the confidence interval of the response at the low (−1) and high (+1) settings of the variable as given in

If the two confidence intervals do not overlap, then the effect is statically significant with a confidence level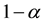 . Practically executed, the regression analysis tests for the significance of the slope tanϑ of each factor, i.e. the coefficients ak of the predictors xk, of the linear regression model,
. Practically executed, the regression analysis tests for the significance of the slope tanϑ of each factor, i.e. the coefficients ak of the predictors xk, of the linear regression model,
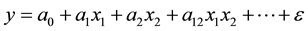
in other word, if the slopes ak are statistically significantly different from zero.
If the null hypothesis H0 (i.e. the population slope is assumed to be zero) is rejected and the decision is to accept the alternative hypothesis HA (i.e. the inference values of ak are supposed to be different from zero) the
Figure 1. Design space of a 3-factor 2-level full factorial DOE with center point.
Figure 2. Response significance to the change of factor level.
factor is statistically significant and has to be retained in the model. The p-value in function of the residual Alpha-risk, also called the significance level, will discriminate between H0 and HA. The p-value gives the probability to incur into a type one error, i.e. the probability to be wrong by rejecting a true null hypothesis. So far so good―but this is only half of the truth.
3. Paying Also Attention to Beta-Risk
Uncertainty has an ambivalent characteristic: randomness and fuzziness. Randomness is related to the stochastic character of a variable (variability of outcome), fuzziness reflects the incomplete knowledge regarding a situation (vagueness of attribution to a binary state). We will not enter here into the discussion of uncertainty reasons but we will apply the classical concept of statistical variability of functional realizations being neither a stochastic nor a fully deterministic response variable. The presence of noise in the system will cause variability of the output following a Z-shaped or rather a t-shaped distribution. The higher the noise, the larger will be the standard deviation of the response.
Due to sampling, we cannot prove equality in statistics but we can only detect differences, with magnitude of this effect to be discovered which can be fixed as small as one likes. If we try to discriminate two values, i.e. realizations of an experiment, we will always have a residual risk which is called Alpha-risk, to incur into a type one error when we reject the null hypothesis of equality, i.e. to see a false-positive effect. If we accept the null hypothesis we will be confident with a confidence level of 1 − α, often set to 95%. In this case we usually talk about confidence and not about probability, because probability is an “ex ante” view of an event. In the case of a sample, the sample statistics have been computed and therefore applying the inferential statistics corresponds to an “ex post” rationalization of the event to draw conclusion about the population parameters. We will reject the null hypothesis, when the conditional probability given by the p-value to incur into a type one error

is smaller than a prefixed accepted residual error risk α (i.e. the significance level of decision) which is usually set to 5% in engineering science
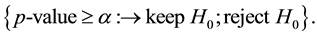
If we do not find enough evidence to reject the null hypothesis this does not mean that the null hypothesis is correct. Indeed, we may incur into a type two error, i.e. retaining the null hypothesis although there is in reality an effect which we did not discover, this means falling into a false-negative trap. This is the Beta-risk. Now, if we reject the null hypothesis and accept the alternative hypothesis, we believe to have detected a significant effect. The question is, is this effect real or is it a just-in-case effect (i.e. effect occurred by chance). Now, what is the probability to detect an effect of a certain magnitude when it exists? This probability 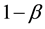 is called power and allows to determine the sensitivity to detect a real effect
is called power and allows to determine the sensitivity to detect a real effect

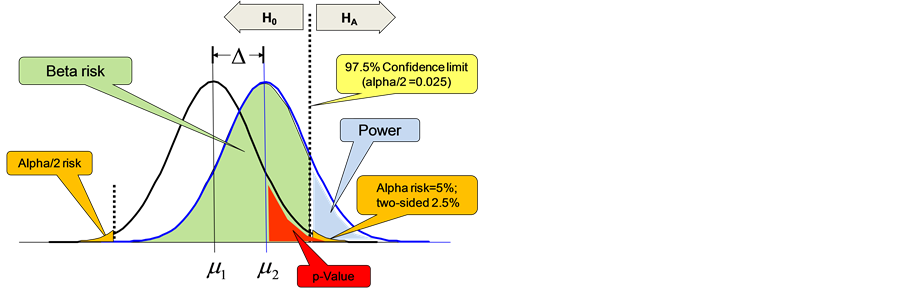
The relations between Alpha, Beta, power and effect Delta are shown in Figure 3 [2] . Interesting is, that the Alpha-risk cannot be reduced without increasing at the same time the Beta-risk because they are coupled; and with increasing Beta-risk the power will decrease to detect a real effect. This shows that it is not enough to limit the probability of being wrong by accepting the alternative hypothesis, we have also to take into consideration the power to detect the desired difference if the difference exists. From Figure 3 it is also observable that with shrinking variation the power increases, variation which is influenced by noise. By modeling the behavior of a system during scientific research we have therefore not to focus only on the mathematical modeling of the physical behavior of the system but especially scientific researchers have to care also about the statistical significance and the sensitivity of the test results, which is often neglected in engineering sciences, contrary to pharmaceutical research.
Figure 4 shows the simplified relationship of the “boundary conditions” in statistical inference to validate a model. It shows the central importance of power and how it is linked to the other variables. Cohen [3] states, the power should be at least 0.8, i.e. in four out of five cases we will detect a difference of a certain prefixed amount. Higher power values more than 0.8 are welcome but will increase sample sizes too much and may lead to the illusion of seeing an effect falling finally into a false-positive trap. Indeed, the more trials one performs, the more likely to incur into a type one error. The sample size n, e.g. for the two-sample mean comparison of the case shown in Figure 3, is given by
Figure 3. Relation between Alpha and Beta-risk to detect an effect Delta.
Figure 4. Simplified systemic boundary conditions determining model validation.

which shows mathematically the relationships of Figure 3 and Figure 4. If the population’s standard deviation Sigma is not known, i.e. the standard deviation has been estimated based on the sample statistics, the Z-distri- bution has to be swapped with the t-distribution with ν degrees of freedom.
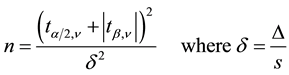
As experience shows, students, if at all, pay only attention to orthogonality and rotatability when setting the design of the experiments but without giving afterwards the necessary attention to the Beta-risk. It is therefore imperatively necessary to document with each research work also the power of detecting an effect in the experimental results. Today, performant statistics packages exist with the specific power metric integrated into DOE software. Great attention should imperatively also be directed to limit the noise of the experiments by identifying the potential sources of noise and how to limit their harmful impact to the response, noise being translated mathematically into a larger standard deviation deteriorating the power. The signal-to-noise ratio, i.e. the F-statistics, has to be maximized in order to declare the effect significant.
4. A Fail-Proof Approach in 14 Steps for Scientific DOE Modeling
In order to avoid pitfalls during experimental modeling we propose the following fail-proof approach in 14 steps (Figure 5) [2] . It shows clearly, that the main attention and effort should be given to the planning phase and less to the modeling. This structured approach eliminates a precipitant experimental proceeding and favors a deliberate course of actions leading to consistent and significant research results. Here we give some additional advice for each step of Figure 5:
1) Describe in words the issue or the objective in order to understand what is to be modeled.
2) Classify the problem as identification or optimization (maximize, minimize, target hitting, robustness).
3) Select a measurable response and, if possible, identify additional interesting ancillary related output variables to be measured during the trials.
4) Conduct imperatively a measurement system analysis (MSA) for the response variables to prove the capability of the measurement system used, or explain why it is not executed. A not capable measurement system immediately invalidates the obtained results.
5) Select appropriate and physically controllable variable factors (e.g. rotor pitch versus rotor revolutions). Identify potential sources of noise and how to deal with them (by fixing, if possible, or by randomizing trials) and define the operational procedures to observe at each trial especially with respect to limiting noise.
6) Select appropriate factor levels covering the whole design space and test the combined settings (e.g. temperature and pressure) that they are feasible and they do not go beyond safety limits. If we are in presence of discrete factor levels, choose the extremes accordingly to allow center point setting. Assign to discrete setting levels with ordinal character continuous and not attributive character (general full factorial); then it is possible to compensate an eventual continuous value of a discrete setting correcting it by another, fully continuous variable. This will also allow to change the operating point stressing robustness of the response by decreasing sensitivity of factor change, especially if noise-influenced.
7) Now we come to the cardinal topic to identify the power of the experiments and the related number of trials, i.e. replicates of the experiment necessary to identify an effect of a certain magnitude. But how to estimate upfront the potential power of the experiment without knowing the variance of the process? If the long term standard deviation of the process, i.e. the population’s standard deviation, is not known a priori, it can be estimated unbiased by approximation with Equation (1), if at least the range of the realizations at a consistent setting level is known, with
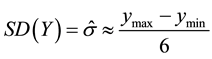 where (1)
where (1)
The here defined range of ±3 standard deviation between ymax and ymin contains 99.7% of the response varia-
Figure 5. Fail-proof DOE approach for scientific research in 14 steps.
tion; outliers apart, this fairly represents the whole process. Or more likely, if the range of variability is not known, the expected sample standard deviation can be estimated with the following proposed Equation (2) without going through variance calculations, conducting only two preliminary trials y1 and y2 at the same setting, if possible at the center point settings to limit impact of potential heteroscedasticity, assuming

Attention, do not confound SD, i.e. the standard deviation of the population with SE, i.e. the standard error of a distribution of sample means. Whereas the Sigma estimated with Equation (1) is the “true” sigma of the process, the standard deviation calculated according to Equation (2) depends on the two realizations y1 and y2. Due to the aleatoric characteristic of repeats or replicates, this leads to a distribution of potential standard deviations dist(sY) of the process estimated according to Equation (2) with the mean E(sY). Such a distribution, performed with a Monte Carlo simulation of a standardized y response with distribution N(0, 1) of 10,000 couples y1 and y2, is shown in Figure 6. It shows, that the mean of the estimated standard deviation according to equation 2, E(sY), is slightly underestimated compared to SD(Y), i.e. 0.8 vs 1,
This bias is of secondary importance because the upfront estimation of the power serves only to approximate the corresponding number of trials and the true power of the experiment has to be evaluated afterwards with the true standard deviation of the experiments. Please note, these approximations have their validity only with the underlying assumption of normally distributed data of the y response.
Further, the power is determined by the Alpha-risk fixed at 5%, by the process’ standard deviation estimated as shown above, by the fixed minimum magnitude of the effect to be detected, and by the sample size. Or if the power is prefixed to suggested 0.8, the minimum effect to be detected with a probability of 80% is now given by the sample size. If the number of replicates and consequent trials to be executed become too much, the minimum detectable effect has to be increased, if that is desirable and possible, to keep the number of trials at a manageable size. At the end of the experiment, the real power of the experiments has to be recalculated; this is now possible knowing the real “within” subgroups variability of the responses. The real power of the response should always be stated with the experimental results.
8) Select according to the previous decisions the design and add some center points to the design. The center point, of course, is unique but it can be repeated as often as one wants, especially when running only one replicate it can be used to estimate the variation of the response. N.B. the addition of the center point does not make a 3-level design out of the DOE, i.e. it remains a 2-level linear model. The center point, in this case, only allows for testing for non-linearity of the model.
Figure 6. Monte Carlo simulated histogram of estimated standard deviations according to Equation (2) for N(0, 1)-standardized y response.
9) Set-up the experiments design in a suitable statistics software package. In research application the factor levels need to be defined with coded units to observe orthogonality of the design. In an orthogonal design the model parameters can be estimated independently. Do not forget to randomize the sequence of the runs. The randomization is absolutely necessary in order to discover long-term variability and to spread the influence of noise over the whole experiments; pay attention in presence of a necessary restricted randomization.
10) Execute the trials with care taking notes in an action log of any deviation from the procedure. This allows, in the case of an abnormal outlier, to repeat just the doubtful trial. Make sure to limit any influence of any nuisance factor.
11) Analyze the data beginning with a graphical overlook of main and interaction effect plots; this gives immediately a first impression. Never rely only on graphical analysis but confirm always analytically the potential significance of effect; indeed, due to scale effects a slope might look to be relevant but this has not to be the case statistically.
12) Build the full model and reduce it step by step with the help of F and t-statistics. If there are not enough degrees of freedom available to carry out the ANOVA (i.e. the error term results to be zero) because of too many terms to be estimated, a provided Pareto-plot based on Lenth’s pseudo standard error for unreplicated experiments may help to select and eliminate non-relevant factors to re-enter in excess trials compared to the number of terms to be estimated, i.e. to release some degrees of freedom. This is possible due to the projective properties of fractional factorial design. Analyze the residuals plot to observe non-normality of residuals distribution, presence of heteroscedasticity in form of an ellipse, butterfly, wedge/fan, or other strange, e.g. curvilinear, residual patterns due to non exhaustive explanation of the variability of the response with the present model. Indeed, heteroscedasticity may lead to the need to take a Bonferroni corrective approach into consideration. Keep also an eye on the autocorrelation of experiment’s sequence.
13) Finally, execute some trials at different settings and compare these with the forecasted results of the model to test the suitability of your model.
14) If the difference is acceptable the model can be used. If the deviations are too big, this might be the consequence of non-linearity. If the test for curvature is negative the lack of fit might be the consequence of too much noise. If the test for curvature results in being significant, you have to go for non-linear modeling.
In the case of non-linearity, the 2-level factorial design allows for expanding the design by adding axial points (called star points) to a so-called Central Composite Design (CCD) keeping valid the trials already executed. Selection of the appropriate alpha-value (N.B. this alpha-value has nothing to do with the Alpha-risk) is essential to maintain the rotatable character of the design. Design rotatability is a searched-for characteristic in DOE design because it maintains the same variability of response for settings having equal distance from the design center; limiting variation increases precision of the model. But be aware: axial points with alpha > 1 go beyond the before fixed proven and safe design space. To avoid this, one can choose a face-centered design with alpha =1 but loosing characteristic of rotatability. Full quadratic models are quite powerful, not needing to build more complex polynomial models.
5. Selecting the Appropriate Type of DOE Modeling
If there are more than 20 variables, it may be opportune to go first for a Screening DOE approach, leaving aside investigation for interaction effects, focusing only on the significance of main effects. This allows the elimination of non-significant terms and to boil down the number of variables to be modeled in the Refining DOE. Usually, Refining DOE as described in the 14 steps approach is often enough to obtain very suitable models. In general, for refining and optimizing DOE, the simplified algorithm shown in Figure 7 [2] can be followed to find which class of DOE model to apply. In the presence of known non-linearity, it may be reasonable to go directly to non-linear Optimizing DOE such as e.g. the Box-Behnken design which has the advantage of having less trials than the CCD. Box-Behnken design is an edge-centered design and is based on multiple polynomial regression of second order
It is a 3-level design with trials remaining in the proven design space and with the factor settings which are never set simultaneously at the high level. This design allows an efficient estimation of 2nd order regression coefficients, although representing only a part of a 3-level full factorial design space; in addition it has rotatable character and allows orthogonal blocking. This is a very efficient non-linear experimental design.
In the case of multiple discrete factor levels, a general full factorial model is needed. In this case it is recommended to limit the factor levels due to power-function-similar increase of the number of trials. Other DOE types exist, such as e.g. Taguchi or D-optimal designs, but the comparison of different DOE types is out of scope of this essay and we refer to the scholastic literature.
Figure 7. Simplified algorithm to select the appropriate type of DOE modeling.
6. Conclusion
DOE modeling is increasingly being applied in industry and science, resulting in a powerful effective technique to identify, in an efficient way, influential variables as well as finding the correct settings to optimize the response. Whereas the application in industrial environment is targeted at identifying the optimal parameter settings of production equipment, and at the same time looks to minimize the number of trials for cost reasons, an indiscriminant and lazy application of statistics boundary conditions may be excusable. But this is not tolerable in an academic environment. In scientific research, the statistical relevance of response of a factor has to comply rigorously with the statistical requirements of minimizing Alpha and Beta-risk. Students have to put serious time and effort into the planning phase of the DOE to limit noise during experimentations and estimate up-front the potential power of their DOE in order not to invalidate the experimental results with a too low power. The here presented easy understandable 14-step approach with explicit focus on Beta-risk is ideally suitable for scientific investigation, guiding statistics-inexperienced students and researchers with a consistent fail-proof approach to obtain statistical significant research results.
References
- Montgomery, D. (2005) Design and Analysis of Experiments. Wiley, New York.
- Rüttimann, B. and Wegener, K. (2015) Einführung in die statistische Versuchsplanung. ETH Tools V Kurs, Lecturing Notes.
- Cohen, J. (1988) Statistical Power Analysis for the Behavioral Sciences. Lawrence Erlbaum Associates, New Jersey.