Positioning
Vol.4 No.1(2013), Article ID:28441,6 pages DOI:10.4236/pos.2013.41011
Relativistic versus Newtonian Frames
![]()
1IMUVA and Departmento de Matemática Aplicada, E.I.I., Universidad de Valladolid, Valladolid, Spain; 2Departmento de Matemática Aplicada, Facultad de Ciencias, Universidad de Valladolid, Valladolid, Spain.
Email: jfpascua@maf.uva.es
Received November 28th, 2012; revised December 30th, 2012; accepted January 10th, 2013
Keywords: Null Emission Coordinates; Location Systems; Causal Class; Relativistic Positioning System; Gravimetry
ABSTRACT
Only a causal class among the 199 Lorentzian ones, which do not exists in the Newtonian space-time, is privileged to construct a generic, gravity free and immediate (non retarded) relativistic positioning system. This is the causal class of the null emission coordinates. Emission coordinates are defined and generated by four emitters broadcasting their proper times. The emission coordinates are covariant (frame independent) and hence valid for any user. Any observer can obtain the values of his (her) null emission coordinates from the emitters which provide him his (her) position and trajectory.
1. Introduction
Globally, the current situation in the Global Navigation Satellite Systems (GNSS) is almost analogous to the following one imagine that a century after Kepler, the astronomers were still using Kepler’s laws as algorithms to correct the Ptolemaic epicycles by means of “Keplerian effects”. Similarly, a century after Einstein, one still uses the Newtonian theory and corrects it by “relativistic or Einsteinian effects” instead of starting with Einstein’s gravitational theory from the beginning.
To show this, we will focus on the essential differences between an old Newtonian plus “relativistic corrections” coming from the post-Newtonian framework, as in the current operating systems which use only the usual class of Newtonian frames, and the new fully relativistic framework which use a new class of relativistic frame: null emission coordinates. Note that there are not “relativistic corrections” in relativity, as they are not “newtonian corrections” in Newtonian theory.
At present the GNSS functioning as global positioning systems, are the GPS and the GLONASS. In general, the satellites (SVs) of the GNSS are affected by Relativity in three different ways: in the equations of motion, in the signal propagation and in the beat rate of the satellite clocks. We will only briefly comment on the clock effects because they are only the measurable ones in the present GNSS and in the future Galileo.
Among the relativistic effects on the rate of the satellite clocks with a time accuracy of nanoseconds and 10−12 of frequency accuracy the most important ones (to first post-Newtonian order ) are: the Einstein effect or gravitational frequency blue shift of the atomic clocks of the satellites (Equivalence principle of General Relativity) with respect to Earth bound clocks due to their position in the Earth gravitational field, time dilation or Doppler shift of second order due to the speed of the satellites (Special Relativity) and the kinematical Sagnac effect due to the rotation of the Earth (Special Relativity), see [1-3] for reviews. If they were not corrected by imposing an offset, the GNSS would not be operative after few minutes. However, with the present and future more accurate clocks (picosecond and even femtosecond), it would be necessary in the Newtonian framework to consider other “relativistic corrections” at post-post-Newtonian order as well as metric spatial curvature effects, tidal effects or delay effects of gravity in the light propagation as the Shapiro time delay.
) are: the Einstein effect or gravitational frequency blue shift of the atomic clocks of the satellites (Equivalence principle of General Relativity) with respect to Earth bound clocks due to their position in the Earth gravitational field, time dilation or Doppler shift of second order due to the speed of the satellites (Special Relativity) and the kinematical Sagnac effect due to the rotation of the Earth (Special Relativity), see [1-3] for reviews. If they were not corrected by imposing an offset, the GNSS would not be operative after few minutes. However, with the present and future more accurate clocks (picosecond and even femtosecond), it would be necessary in the Newtonian framework to consider other “relativistic corrections” at post-post-Newtonian order as well as metric spatial curvature effects, tidal effects or delay effects of gravity in the light propagation as the Shapiro time delay.
In this situation, it can be wondered if it would not be more convenient to change the present Newtonian framework to an exact formulation in full General Relativity. This would imply to abandon the classical post-Newtonian framework for the description of GNSS. The root of this radical change is the consideration of a new 4D proper relativistic frame (emission coordinates) instead of the usual Newtonian frame, which uses 3D spatial reference systems, such as the ECI (Earth Centered Inertial system) or the ECEF (Earth Centered Earth Fixed system), and a time reference (GPS time), separately.
Emission coordinates were firstly introduced by B. Coll in a pioneering proposal published in [4]. To discuss and understand the meaning of the null emission coordinate system is necessary to introduce previously some new definitions, as such location systems or causal classification of frames, and mathematical physics tools, mainly geometrical. These new definitions and tools provide a clear way to understand the differences among the special subclass of Newtonian frames and the general class of relativistic frames.
2. Location Systems
Location systems are physical realizations of 4D coordinate systems. Hence there is a differentiation of a coordinate system as a mathematical object from its realization through physical objects and protocols. A location system is thus a precise protocol on a set of physical fields allowing to materialize a coordinate system. However, different physical protocols, involving different physical fields, may be given for a unique mathematical coordinate system.
A location system must include the protocols for the physical construction of the coordinate lines, coordinate surfaces or coordinate hypersurfaces of specific causal orientations of the coordinate system that it realizes. Thus, for instance, these coordinate elements may be realized by means of clocks for time-like lines, laser pulses for null lines, synchronized inextensible threads for space-like lines, laser beams or inextensible threads for time like surfaces and light-front surfaces for null hypersurfaces. The different protocols involved in the construction of location systems give rise to coordinate elements (lines, surfaces and hypersurfaces) of different causal orientations, i.e., they realize coordinate systems of different causal nature.
2.1. Reference Systems
Location systems are of two different types: reference systems and positioning systems. The first ones are 4D reference systems which allow one observer, considered at the origin, to assign four coordinates to the events of its neighborhood by means of electromagnetic signals. In relativity due to the finite speed of the transmission of information, this assignment is retarded with a time delay.
A paradigmatic reference system in relativity is the radar system which is based in the Poincaré protocol of synchronization which uses two-way light signals from the observer to the events to be coordinated. Unfortunately, the radar system suffers from the bad property of being constructed from a retarded protocol due to the finite speed of the transmission of information.
2.2. Positioning Systems
The second kind of location systems are 4D positioning systems, which allow to every event of a given domain to know its proper coordinates in an immediate or instantaneous way without delay. In addition to be immediate, the positioning systems must verify other two conditions, they must be generic and free of gravity. A positioning system is generic, if it can be constructed in any spacetime and, it is free of gravity, if the knowledge of the gravitational field is not necessary to construct it. Reference systems privilege one specific observer among all others, whereas in positioning systems no observers are necessary at all and hence there is no necessity of any synchronization procedure between different observers.
In relativity, a (retarded) reference system can be constructed starting from an (immediate) positioning system, it is sufficient that each event sends its coordinates to the observer at the origin of the reference system, but not the other way around. In contrast, in Newtonian theory, 3D reference and positioning systems are interchangeable and as the velocity of transmission of information is infinite, the Newtonian reference systems are not retarded but immediate. The reference and positioning systems defined here are 4-dimensional objects, including time location.
3. Causal Classification of Frames
In the Lorentzian space-time of general relativity, directions and planes or hyperplanes of directions at any event are said to be space-like, light-like (or null or isotropic) or time-like oriented if they are respectively exterior, tangent or secant to the light-cone of this event. These causal orientations can be extended in a natural way to vectors, covectors and volume forms on these sets of directions. Thus, every one of the vectors  of a frame of the tangent space
of a frame of the tangent space ,
, 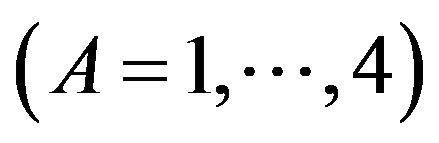 has a particular causal orientation
has a particular causal orientation .
.
However, the causal orientations 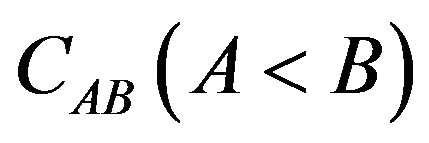 of the six different associated or adjoint planes
of the six different associated or adjoint planes  of the frame
of the frame  are not determined by the specific causal orientations
are not determined by the specific causal orientations 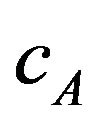 of the vectors of the frame. For instance, the plane associated to two space-like vectors may have any causal orientation. So, in general, the causal characters
of the vectors of the frame. For instance, the plane associated to two space-like vectors may have any causal orientation. So, in general, the causal characters 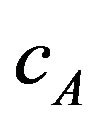 and
and 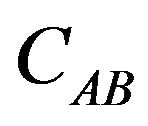 are independent. Moreover, in order to give a complete description of the causal properties of the frames, one needs also to specify the causal orientations
are independent. Moreover, in order to give a complete description of the causal properties of the frames, one needs also to specify the causal orientations  of the four covectors or 1-forms
of the four covectors or 1-forms  giving the dual coframe
giving the dual coframe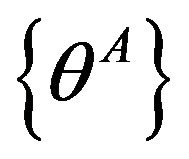 , i.e.
, i.e. . Following [5], the best way to visualize and characterize a space-time coordinate system is to start from four families of coordinate 3-surfaces, then their mutual intersections give six families of coordinate 2-surfaces and four congruences of coordinate lines.
. Following [5], the best way to visualize and characterize a space-time coordinate system is to start from four families of coordinate 3-surfaces, then their mutual intersections give six families of coordinate 2-surfaces and four congruences of coordinate lines.
Alternatively, one can use the related covectors or 1- forms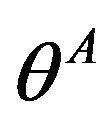 , instead of the 3-surfaces, and the vectors of a coordinate tangent frame
, instead of the 3-surfaces, and the vectors of a coordinate tangent frame  instead of four congruences of coordinate lines which are their integral curves. The covector
instead of four congruences of coordinate lines which are their integral curves. The covector  is time-like (resp. space-like) iff the 3-plane
is time-like (resp. space-like) iff the 3-plane 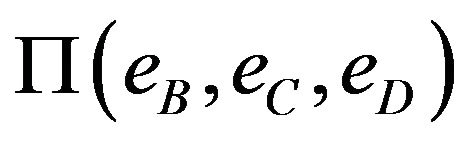 generated by the three vectors
generated by the three vectors 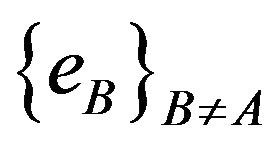 is space-like (resp. time-like). This applies for both Newtonian and Lorentzian space-times. In addition, for the latter, the covector
is space-like (resp. time-like). This applies for both Newtonian and Lorentzian space-times. In addition, for the latter, the covector  is light-like (or null) iff the 3-plane generated by
is light-like (or null) iff the 3-plane generated by 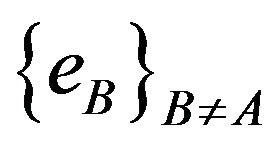 is light-like (or null). Thus, to specify the causal orientations of hyperplanes is not necessary because is redundant with the causal orientation of the covectors.
is light-like (or null). Thus, to specify the causal orientations of hyperplanes is not necessary because is redundant with the causal orientation of the covectors.
In this way, for a specific domain of a Lorentzian or Newtonian space-time, each frame  is fully characterized by its causal class. The causal class of a frame is the set of all the frames that have same causal signature, which is defined by a set of 14 causal characters:
is fully characterized by its causal class. The causal class of a frame is the set of all the frames that have same causal signature, which is defined by a set of 14 causal characters:
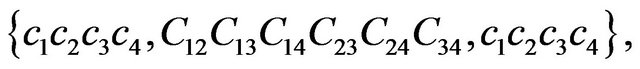
As notation for the causal characters, we will use lower case roman types 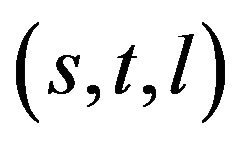 to represent the causal character of vectors (resp. space-like, time-like, lightlike), and capital types
to represent the causal character of vectors (resp. space-like, time-like, lightlike), and capital types 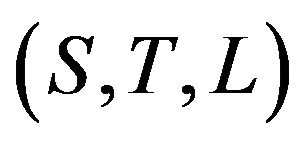 and lower case italic types
and lower case italic types 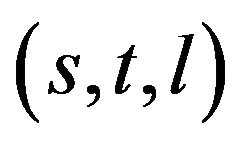 to denote the causal character of 2-planes and covectors, respectively.
to denote the causal character of 2-planes and covectors, respectively.
3.1. Relativistic Frames
This new degree of freedom (light-like) in the causal character, which is proper of Lorentzian relativistic space-times but which does not exist in Newtonian space-times, allows to obtain (see [5,6]), as it has been commented in the abstract, the following theorem:
In a relativistic 4-dimensional Lorentzian space-time, there exists 199, and only 199, causal classes of frames.
These 199 causal classes have been completely classified.
We shall see that among the 199 Lorentzian causal classes, only one is privileged to construct a generic, gravity free and immediate positioning system.
The notion of causal class extends naturally to the set of coordinate lines of the coordinate system and so, to the coordinate system itself. By definition, the causal class of a coordinate system 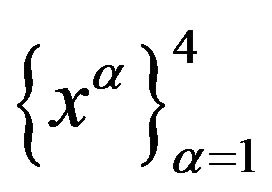 in a domain is the causal class
in a domain is the causal class 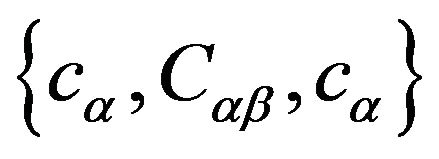 of its associated natural frame at the events of the domain. In relativity, a specific causal class, among the 199 ones, can be assigned to any of the different coordinate systems used in all the solutions of the Einstein equations. However, for the same coordinate system and the same solution, the causal class can change depending on the region of the space-time considered and the coordinate system in this case is said to be inhomogeneous.
of its associated natural frame at the events of the domain. In relativity, a specific causal class, among the 199 ones, can be assigned to any of the different coordinate systems used in all the solutions of the Einstein equations. However, for the same coordinate system and the same solution, the causal class can change depending on the region of the space-time considered and the coordinate system in this case is said to be inhomogeneous.
In fact, see [7], in any space-time every coordinate 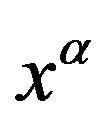 plays two extreme roles: that of a hypersurface for every constant value
plays two extreme roles: that of a hypersurface for every constant value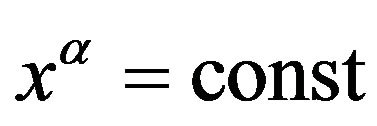 , of gradient
, of gradient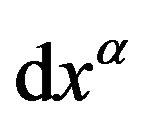 , and that of a coordinate line of tangent vector
, and that of a coordinate line of tangent vector , when the other coordinates remain constant. This simple fact shows that, in spite of the historical custom of associating to a coordinate a causal orientation, saying that it is time-like, light-like or space-like, this appellation is not generically coherent. Causal orientations are generically associated with directions of geometric objects, but not with spacetime coordinates associated to them. In the case of a coordinate
, when the other coordinates remain constant. This simple fact shows that, in spite of the historical custom of associating to a coordinate a causal orientation, saying that it is time-like, light-like or space-like, this appellation is not generically coherent. Causal orientations are generically associated with directions of geometric objects, but not with spacetime coordinates associated to them. In the case of a coordinate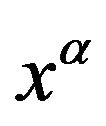 , this generic incoherence appears because its two natural variations in the coordinate system,
, this generic incoherence appears because its two natural variations in the coordinate system, 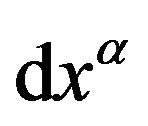 and
and , have generically different causal orientations. Only when both causal orientations coincide, it is possible to extend to the coordinate
, have generically different causal orientations. Only when both causal orientations coincide, it is possible to extend to the coordinate  itself the character of the common causal orientation of its two mentioned variations.
itself the character of the common causal orientation of its two mentioned variations.
3.2. Newtonian Frames
The differences in the geometric description of Lorentzian and Newtonian frames come from the causal structure induced by the different metric descriptions of Lorentzian and Newtonian space-times. The main difference comes essentially from the absence of the lightlike character in the Newtonian case. In relativity, the space-time metric is non-degenerate and defines a oneto-one correspondence between vectors and covectors at the tangent and cotangent space of every event.
In contrast, in a Newtonian space-time no non-degenerate metric structure exists and one has two different metrics, see [8]. This degenerate metric structure is given by a rank one covariant time metric 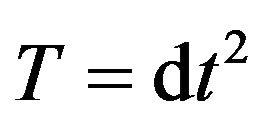 and an orthogonal rank three contravariant space metric
and an orthogonal rank three contravariant space metric . In the time metric appears t, which is an absolute time scale and the hypersurfaces t = const, constitute the instantaneous or simultaneity spaces. A vector
. In the time metric appears t, which is an absolute time scale and the hypersurfaces t = const, constitute the instantaneous or simultaneity spaces. A vector![]() is space-like if it is instantaneous, i.e. if
is space-like if it is instantaneous, i.e. if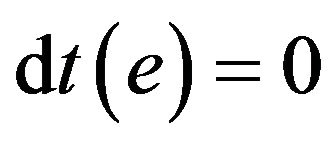 . Otherwise, it is timelike. So, it is clear that a frame can have at most three space-like vectors so, there only exist four causal types of Newtonian frame bases, namely:
. Otherwise, it is timelike. So, it is clear that a frame can have at most three space-like vectors so, there only exist four causal types of Newtonian frame bases, namely: ,
,  ,
,  ,
, .
.
Correspondingly, a covector 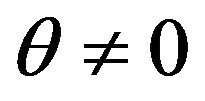 is time-like if it has no instantaneous part with respect to the contravariant space metric
is time-like if it has no instantaneous part with respect to the contravariant space metric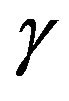 , i.e. if
, i.e. if 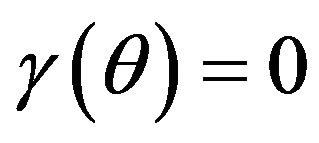 and it is necessarily of the form
and it is necessarily of the form  with
with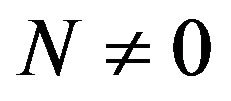 , being future (resp. past) oriented if
, being future (resp. past) oriented if  (resp.
(resp.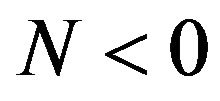 ). Otherwise, the covector
). Otherwise, the covector  is space-like. Thus, attending to the causal orientation of their covectors, there only exist two causal types of Newtonian coframes bases:
is space-like. Thus, attending to the causal orientation of their covectors, there only exist two causal types of Newtonian coframes bases: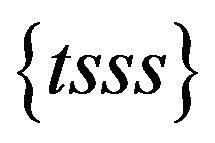 ,
,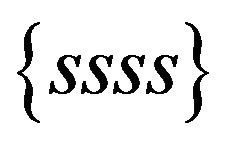 .
.
In summary, it can be shown (see [7]) that one has the following implications valid only for Newtonian frames:
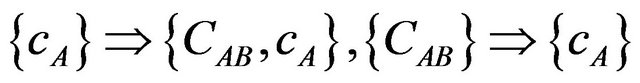 .
.
The simplicity of the Newtonian causal structure with respect to the Lorentzian one, lies in the fact that the causal type of a Newtonian frame determines completely its causal class. This is related to the fact that, in Newtonian space-time, any set of space-like vectors always generates a space-like subspace. As a consequence, the number of causally different Newtonian classes of frames is equal to the dimension of the space-time. Hence, see [7], in the 4-dimensional Newtonian space-time there exist four, and only four, causal classes of frames. They are:
 ,
,  ,
,
 and
and .
.
4. Relativistic Positioning
4.1. Coll Positioning System
As it has been commented above, among the 199 Lorentzian causal classes, in which the four Newtonian ones are included, only one is privileged to construct a generic (valid for a wide class of spacetimes), gravity free (the previous knowledge of the gravitational field is not necessary) and immediate relativistic positioning system.
This is the causal class {s s s s; S S S S S S; l l l l} of the Coll homogeneous coordinate system [2,4,5]. In this causal class the null emission coordinates of the Coll positioning system are included. These emission coordinates have been also studied in [9-11] in the special case of a flat Minkowski space-time without gravity.
The coordinate system of this causal class is always homogeneous and it has associated four families of null 3-surfaces or equivalently a real non-orthogonal null coframe, whose mutual intersections give six families of spacelike 2-surfaces and four congruences of space-like lines. Such a coordinate system does not exist in a Newtonian space-time where the light travels at infinite speed. One satellite clock broadcasting its proper time is described in the space-time by a time-like line , in which each event of proper time
, in which each event of proper time  is the vertex of a future light cone. The set of these four light cones of an emitter constitutes a one-parameter (proper time) family of null hypersurfaces. So, four satellite clocks broadcasting their proper times determine four one-parameter families of lightlike 3-surfaces (future light cones), see Figure 1. Thus, the Coll positioning system makes use of the mathematical theorem that four future light cones generically intersect in an unique event, which is just the spacetime position of the receiver or user.
is the vertex of a future light cone. The set of these four light cones of an emitter constitutes a one-parameter (proper time) family of null hypersurfaces. So, four satellite clocks broadcasting their proper times determine four one-parameter families of lightlike 3-surfaces (future light cones), see Figure 1. Thus, the Coll positioning system makes use of the mathematical theorem that four future light cones generically intersect in an unique event, which is just the spacetime position of the receiver or user.
In this relativistic positioning system, any receiver or user at any event in a given spacetime region can know its proper coordinates. The four proper times of four satellites  read at an event by a receiver or user constitute the null (or light) proper emission coordinates or user positioning data of this event, with respect to four SVs, see Figure 2. These four numbers or parameters can be understood as the “distances” between
read at an event by a receiver or user constitute the null (or light) proper emission coordinates or user positioning data of this event, with respect to four SVs, see Figure 2. These four numbers or parameters can be understood as the “distances” between
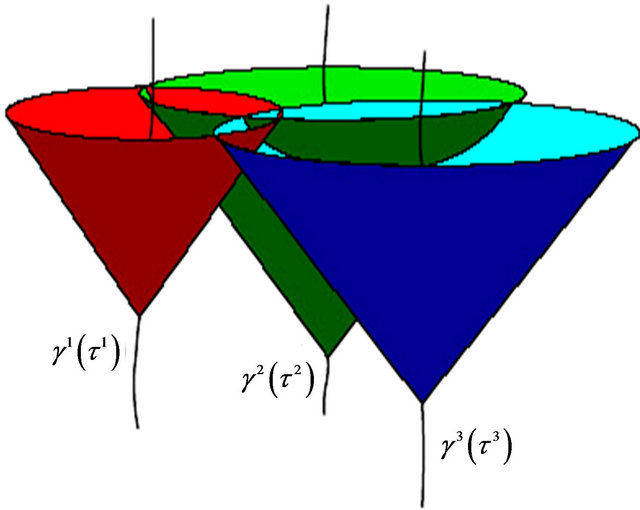
Figure 1. Relativistic emission coordinates: intersection of the four future light cones of the SVs with the past light cone of a receiver. In the Figure only 3 light cones of the SVs are drawn in a Lorentzian space-time of 1 + 2 dimensions.
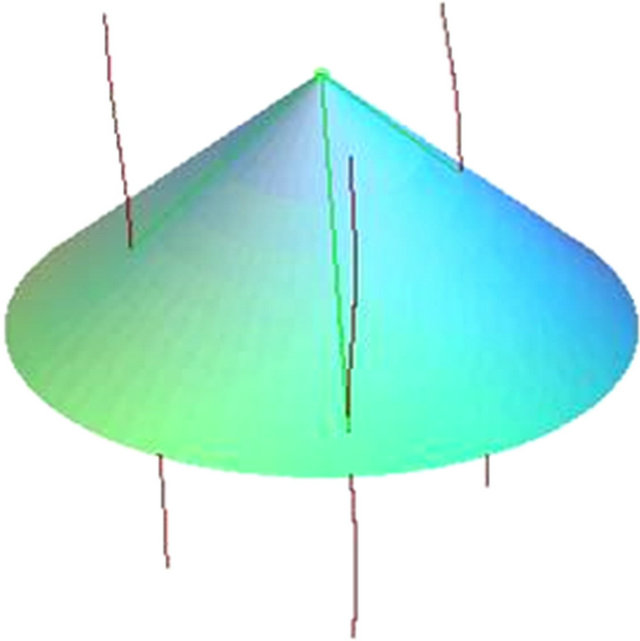
Figure 2. Past light cone of an event in 3 dimensions, the proper time parameterized paths of 3 SVs (in violet) and the lightlike geodesics (in green) followed by the signal from each satellite to an event of the trajectory of a receiver.
the reception event and the four satellites. In a certain domain of R4 of the grid Ω of parameters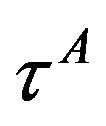 , any user receiving continuously his null emission coordinates from four satellites may know his trajectory in the grid of parameters. If the observer has his own clock, with proper time denoted by
, any user receiving continuously his null emission coordinates from four satellites may know his trajectory in the grid of parameters. If the observer has his own clock, with proper time denoted by ![]() then he can know his trajectory with proper time parametrization,
then he can know his trajectory with proper time parametrization,  , and his four-velocity,
, and his four-velocity,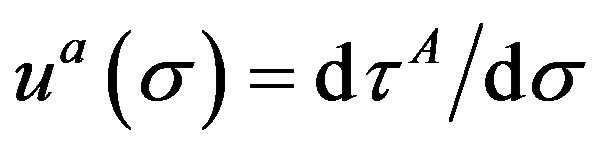 .
.
For positioning out a GNSS constellation, i.e. for interplanetary missions in the Solar system, a “pulsar” Coll relativistic positioning system can be conceived, see [12, 13], based on the X-ray signals of four properly selected stable millisecond pulsars and a conventional origin of the emission coordinates. On the other hand, a navigation project called XNAV (based in pulsars) is being developed during the last years by DARPA and NASA but unfortunately, see [14], is based in the same Newtonian concepts that the GPS or Galileo. However, in this case, it is more complicated because post-post-Newtonian corrections must be implemented.
4.2. Contravariant Metric in Emission Coordinates
As the emission coordinates belong to the causal class {s s s s; S S S S S S; l l l l}, there is not a spacetime asymmetry like in the standard Newtonian coframe (t s s s) (one timelike “t” and three spacelike “s”). In emission coordinates obtained from a general real null co-frame (l l l l) =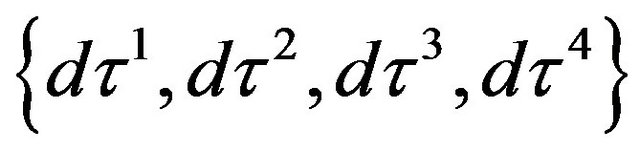 , which is neither orthogonal nor normalized, the contravariant spacetime metric is symmetric with null diagonal elements and it has the general expression, see [2,15]:
, which is neither orthogonal nor normalized, the contravariant spacetime metric is symmetric with null diagonal elements and it has the general expression, see [2,15]:
 (2)
(2)
where 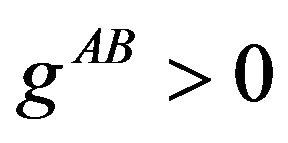 for
for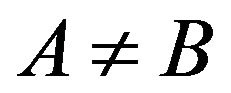 . Four null covectors can be linearly dependent although none of them is proportional to another. To ensure that the four null covectors are linearly independent and span a 4-dim space-time, it is sufficient that det
. Four null covectors can be linearly dependent although none of them is proportional to another. To ensure that the four null covectors are linearly independent and span a 4-dim space-time, it is sufficient that det . Finally, this metric has a Lorentzian signature (+, −, −, −) iff
. Finally, this metric has a Lorentzian signature (+, −, −, −) iff .
.
The expression (2) of the metric is observer independent and has six degrees of freedom. In the terminalogy of [9], the proper times 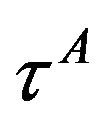 are partial observables, while the components of the metric
are partial observables, while the components of the metric 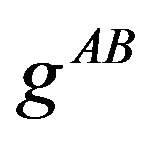 are complete observables, i.e., gauge independent or invariant quantities under diffeomorphisms in the Lorentzian spacetime.
are complete observables, i.e., gauge independent or invariant quantities under diffeomorphisms in the Lorentzian spacetime.
A splitting of this metric can be considered, see [15], changing from the six independent components (ten components minus four gauge degrees of freedom of coordinate transformations) of  to a more convenient set, which neatly separates two shape parameters depending only on the direction of the covectors
to a more convenient set, which neatly separates two shape parameters depending only on the direction of the covectors  or equivalently depending exclusively on the trajectories of the emitters, from other four scaling parameters depending on the length of the covectors or depending on the proper time of each satellite.
or equivalently depending exclusively on the trajectories of the emitters, from other four scaling parameters depending on the length of the covectors or depending on the proper time of each satellite.
4.3. SYPOR Project: Autolocated Positioning System
SYPOR project is the anagram (in French) of Relativistic Positioning System project. The basic idea of this project, that was conceived by Coll in [6] and also exposed in [2, 3], is the following one: A satellite constellation provided with clocks that interchange their proper time among them (interlinks) and with Earth receivers, is a fully relativistic autonomous or autolocated positioning system. Note that, nowadays, this procedure of proper time auto navigation can be technically fulfilled.
In the SYPOR, the segment of Control is in the constellation of satellites, see Figure 3. The function of this
Figure 3. In the SYPOR, the Space and Control segments coincide with the constellation.
new Control segment is not to determine the ephemerides of the satellites with respect to geocentric coordinates as in the newtonian GNSS, but to determine the null emission coordinates of the receivers with respect to the constellation of SVs. Therefore, the procedure used until now in the newtonian GNSS is inverted.
Let us define properly what means autonomous or autolocated. Four satellites emitting, without the necessity of a synchronization convention, not only their proper times , but also the proper times
, but also the proper times 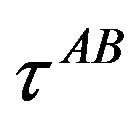 of the three close satellites received by the satellite A in
of the three close satellites received by the satellite A in 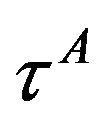 (in total sixteen emitter positioning data
(in total sixteen emitter positioning data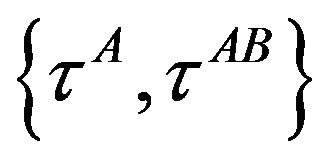 ;
;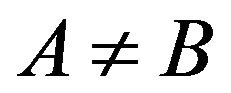 ;
; ), constitute an autolocated positioning system.
), constitute an autolocated positioning system.
In an autolocated positioning system, the receivers can know not only its spacetime path but also the trajectories of the four satellites in the grid of R4 of emission coordinates.
5. Gravimetry and Positioning
In General Relativity, the gravitational field is described by the space-time metric. If this metric is exactly known a priori, the system just described will constitute an ideal positioning system. In practice, the actual space-time metric (i.e., the gravitational field) is not exactly known (in the GPS it is supposed to be essentially the Schwarzschild metric) and the satellite system itself has to be used to infer it. This problem arises when a satellite system is used for both positioning and gravimetry.
To solve this joint problem, the considered satellites should have more than one clock: they may carry an accelerometer providing information on the space-time connection. Of course, in first approximation the satellites are in free-fall and consequently have zero acceleration. However, we are considering here the realistic case where the acceleration is nonzero due, for instance, to a small drag in the high atmosphere and this is measured by the accelerometers. Also, the satellites may have a gradiometer, this would give additional information on the metric (in fact, on the Riemann tensor of the space-time).
With these data (and perhaps some additional ones) an optimization procedure could be developed (see [16]) to obtain the best observational gravitational field acting actually on the constellation. The problem of obtaining the space-time metric is a kind of inverse problem since one wants to recover the spacetime metric from the observed data in the Coll positioning system.
5.1. Two Dimensional Cases
Coll positioning systems are yet now quite well developed for two-dimensional space-times, see [11,17] where several results have been developed. For instance, the knowledge that the positioning system is stationary and that the space-time is created by a given mass, allows to know the accelerations of the emitters, their mutual radar distances and the space-time metric in null emission coordinates. The important point for gravimetry is that the Schwarzschild mass may be substituted by that of the acceleration of one of the emitters.
5.2. Realistic Four Dimensional Cases
For applications of an autolocated positioning system on or near the Earth’s surface, the primary emission coordinates should be related to some terrestrial secondary 4-dimensional Newtonian coordinate system. This problem has been solved for a general configuration of the emitters in flat Minkowski space-time [18,19] and also for the case of a special configuration of the emitters in a Schwarzschild spacetime [20].
However, in general the known results for the flat and curved two dimensional spacetimes are not trivially generalizable for the realistic curved four dimensional one [15] and much work remains to be done in the future.
6. Acknowledgements
One of the authors (JFPS) is grateful to Bartolomé Coll by communications on this subject along several years. This work was partially supported by the Spanish Ministerio de Educación y Ciencia, MEC-FEDER ESP2006- 01263 grant.
REFERENCES
- N. Ashby, “Relativity in the Global Positioning System,” Living Reviews in Relativity, Vol. 6, 2003, p. 1.
- J.-F. Pascual-Sánchez, “Introducing Relativity in Global Navigation Satellite Systems,” Annalen der Physik, Vol. 16, No. 4, 2007, pp. 258-273. doi:10.1002/andp.200610229
- J.-F. Pascual-Sánchez, “The Relativistic Framework of Positioning Systems,” First Colloquium on Scientific and Fundamental Aspects of the Galileo Program, 2007, arXiv:0710.1282.
- B. Coll, “Reference Frames and Gravitomagnetism,” World Scientific, Singapore, 2001, p. 53.
- B. Coll and J. A. Morales, “199 Causal Classes of SpaceTime Frames,” International Journal of Theoretical Physics, Vol. 31, 1992, p. 1045.
- B. Coll, “Physical Relativistic Frames,” Proc. Jour. Sys. Ref. Spat. Temp., Brussels, ed N. Capitaine, Observatoire de Paris, 2001, p. 169.
- B. Coll, J. J. Ferrando and J. A. Morales, “Four Causal Classes of Newtonian Frames,” Foundations of Physics, Vol. 39, 2009, p. 1280.
- A. Trautman, “Sur la Théorie Newtonienne de la Gravitation,” Comptes Rendus de l'Académie des Sciences, Vol. 257, 1963, p. 617.
- C. Rovelli, “GPS Observables in General Relativity,” Physical Review D, Vol. 65, No. 4, 2002, Article ID: 044 017. doi:10.1103/PhysRevD.65.044017
- M. Blagojevic, J. Garecki, F. W. Hehl and Yu. N. Obukhov, “Real Null Coframes in General Relativity and GPS Type Coordinates,” Physical Review D, Vol. 65, No. 4, 2002, Article ID: 044018. doi:10.1103/PhysRevD.65.044018
- B. Coll, J. J. Ferrando and J. A. Morales, “Two-Dimensional Approach to Relativistic Positioning Systems,” Physical Review D, Vol. 73, No. 8, 2006, Article ID: 084 017. doi:10.1103/PhysRevD.73.084017
- A. Tarantola and B. Coll, “Using Pulsars to Define SpaceTime Coordinates,” 2009, arXiv:0905.4121.
- M. L. Ruggiero, E. Capolongo and A. Tartaglia, “Pulsars as Celestial Beacons to Detect the Motion of the Earth,” International Journal of Modern Physics, Vol. 20, No. 6, 2011, pp. 1025-1038.
- P. Graven, et al., “XNAV for Deep Space Navigation,” Proceedings of 31st Annual AAS Guidance and Control Conference, AAS 08-054, 2008.
- B. Coll and J. M. Pozo, “Relativistic Positioning Systems: The Emission Coordinates,” Classical and Quantum Gravity, Vol. 23, No. 24, 2006, p. 7395. doi:10.1088/0264-9381/23/24/012
- A. Tarantola, L. Klimes, J. M. Pozo and B. Coll, “Gravimetry, Relativity, and the Global Navigation Satellite Systems,” 2009, arXiv:0905.3798.
- B. Coll, J. J. Ferrando and J. A. Morales, “Positioning with Stationary Emitters in a Two-Dimensional SpaceTime,” Physical Review D, Vol. 74, No. 10, 2006, Article ID: 104003. doi:10.1103/PhysRevD.74.104003
- M. Lachièze-Rey, “The Covariance of GPS Coordinates and Frames,” Classical and Quantum Gravity, Vol. 23, No. 10, 2006, p. 3531. doi:10.1088/0264-9381/23/10/019
- B. Coll, J. J. Ferrando and J. A. Morales-Lladosa, “Positioning Systems in Minkowski Spacetime: From Emission to Inertial Coordinates,” Classical and Quantum Gravity, Vol. 27, No. 6, 2010, Article ID: 065013. doi:10.1088/0264-9381/27/6/065013
- D. Bini, A. Geralico, M. L. Ruggiero and A. Tartaglia, “Emission versus Fermi Coordinates: Applications to Relativistic Positioning Systems,” Classical and Quantum Gravity, Vol. 25, No. 20, 2008, Article ID: 205011. doi:10.1088/0264-9381/25/20/205011

