Natural Science
Vol.6 No.7(2014), Article ID:45363,7 pages DOI:10.4236/ns.2014.67054
Discussing an Expected Utility and Weighted Entropy Framework
José Pinto Casquilho
Post-Graduate and Research Program, Universidade Nacional Timor Lorosa’e, Díli, Timor Leste (East Timor)
Email: josecasquilho@gmail.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 25 December 2013; revised 25 January 2014; accepted 1 February 2014
ABSTRACT
In this paper, it is discussed a framework combining traditional expected utility and weighted entropy (EU-WE)—also named mean contributive value index—which may be conceived as a decision aiding procedure, or a heuristic device generating compositional scenarios, based on information theory concepts, namely weighted entropy. New proofs concerning the maximum value of the index and the evaluation of optimal proportions are outlined, with emphasis on the optimal value of the Lagrange multiplier and its meaning. The rationale is a procedure of maximizing the combined value of a system expressed as a mosaic, denoted by characteristic values of the states and their proportions. Other perspectives of application of this EU-WE framework are suggested.
Keywords:Mosaic Composition, Expected Utility, Weighted Entropy, Mean Contributive Value

1. Introduction
Shannon entropy has been widely used in ecological studies as a measure of diversity at different scales in space, from local community level to landscapes and regions. Guiasu and Guiasu [1] [2] provide an extensive literature review covering the properties and applications of these measures of diversity in general, and, concerning landscape metrics, there are also several reviews of the theme, (e.g., [3] -[5] ), Shannon entropy being recommended for landscape management as it is considered an index sensitive to the presence of rare habitats [6] .
The core of the rationale that relates utility and information theory concepts can be summarized as it was stated by Bernardo [7] , recognizing the decision problem underlying a problem of statistical inference: expected information may be conceived as expected utility.
1.1. Statistical Entropy and Diversity
Under the scope of a general theory of communication, Shannon [8] defined entropy as a measure of how much choice is involved in the selection of an event, or of how uncertain we are of the outcome, and settled the formula 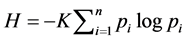 where the constant
where the constant ![]() merely amounts to a choice of a unit of measure. Heretrieved previous work of Hartley [9] outlining a quantitative measure whereby the capacities of various systems to transmit information might be compared, taking a measure of information as the logarithm of the number of possible symbol sequences. Jaynes [10] wrote that entropy as a concept may be regarded as a measure of our degree of ignorance as to the state of a system and that quantity
merely amounts to a choice of a unit of measure. Heretrieved previous work of Hartley [9] outlining a quantitative measure whereby the capacities of various systems to transmit information might be compared, taking a measure of information as the logarithm of the number of possible symbol sequences. Jaynes [10] wrote that entropy as a concept may be regarded as a measure of our degree of ignorance as to the state of a system and that quantity 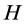 measures in a unique way the amount of uncertainty represented by a probability distribution. Also, entropy is claimed to be a measure of the average randomness of a stochastic system [11] and it is referred to be the only meaningful functional for measuring uncertainty and information in probability theory [12] . The information value of an event is defined as
measures in a unique way the amount of uncertainty represented by a probability distribution. Also, entropy is claimed to be a measure of the average randomness of a stochastic system [11] and it is referred to be the only meaningful functional for measuring uncertainty and information in probability theory [12] . The information value of an event is defined as 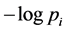 so formula H denotes the mean information value of a sample space, related to the coexistence of a multi-state system or a mosaic.
so formula H denotes the mean information value of a sample space, related to the coexistence of a multi-state system or a mosaic.
Rènyi [13] generalized Shannon entropy as a 1-parameter functional family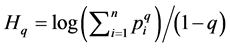 , under the scope of measures of entropy and information defined on the set of generalized probability distributions, entailing that
, under the scope of measures of entropy and information defined on the set of generalized probability distributions, entailing that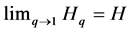 . Rènyi generalized entropy function has been recently referred to as a continuum of diversity measures [14] . Hill [15] proved that the exponential form of Rènyi entropies
. Rènyi generalized entropy function has been recently referred to as a continuum of diversity measures [14] . Hill [15] proved that the exponential form of Rènyi entropies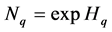 —he called diversity numbers—has an immediate connection with diversity indices used in Ecology: the richness in species, the exponential form of Shannon entropy and the inverse of Simpson’s index.
—he called diversity numbers—has an immediate connection with diversity indices used in Ecology: the richness in species, the exponential form of Shannon entropy and the inverse of Simpson’s index.
1.2. Weighted Entropy and Utility
Weighted entropy was first proposed by Bellis and Guiasu [16] taking into account the two basic concepts of objective probability and subjective utility, thus defining the information supplied by the event ![]() with a probability
with a probability ![]() and an utility
and an utility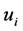 —the last meaning the value of an outcome relative to a specified goal—with the formula
—the last meaning the value of an outcome relative to a specified goal—with the formula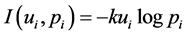 , and k > 0. Guiasu [17] derived the principle of maximum information obtaining the probability distribution maximizing weighted entropy—he later called useful entropy [18] —and Aggarwal and Picard [19] settled a general overview of information measures with preference, the preference of an event being defined as the product of its probability and utility. Several applications with weighted entropy were performed in the middle eighties: for instance, Batty [20] used weighted entropy to discuss the spatial pattern of aggregation in cities, while Nawrocki and Harding [21] used state-value weighted entropy as a measure of investment risk; Taneja and Tuteja [22] extended the concept to derive the characterization of a quantitative-qualitative measure of inaccuracy. Later, Guiasu and Guiasu [23] revised the theme under ecology analysis, noting that, whenever measuring the diversity of ecosystems, additional information—such as absolute abundance, economic significance or ecological importance of species—has to be taken into account, reflected in the weights, a concept that was further extended to joint weighted entropy related to the joint probability distribution assigned to pairs of species [24] .
, and k > 0. Guiasu [17] derived the principle of maximum information obtaining the probability distribution maximizing weighted entropy—he later called useful entropy [18] —and Aggarwal and Picard [19] settled a general overview of information measures with preference, the preference of an event being defined as the product of its probability and utility. Several applications with weighted entropy were performed in the middle eighties: for instance, Batty [20] used weighted entropy to discuss the spatial pattern of aggregation in cities, while Nawrocki and Harding [21] used state-value weighted entropy as a measure of investment risk; Taneja and Tuteja [22] extended the concept to derive the characterization of a quantitative-qualitative measure of inaccuracy. Later, Guiasu and Guiasu [23] revised the theme under ecology analysis, noting that, whenever measuring the diversity of ecosystems, additional information—such as absolute abundance, economic significance or ecological importance of species—has to be taken into account, reflected in the weights, a concept that was further extended to joint weighted entropy related to the joint probability distribution assigned to pairs of species [24] .
Casquilho et al. [25] derived independently the main results concerning weighted entropy, under a 1-parameter generalization of Shannon formula focused on an ecological and economic application at the landscape level, from which followed the EU-WE framework here discussed—weighted entropy was then named mean informative value index and EU-WE framework was defined as mean contributive value index. These results were applied to discuss compositional scenarios of forest ecomosaics [26] -[28] , with a non-linear utility scope where the concept of contributive value plays a central role: contributive value is a relational form of value, it is the value that some part confers on the whole of which it is a part, because this contribution is conditioned by the presence and extent of other parts [29] , so emphasizing that the contributive value of a part should not be confused with the value that this part has on its own, independently from the context [30] . The value that a part has on its own was referred to as a characteristic, or intrinsic, value.
Ricotta [31] mentioned weighted entropy as a contribute towards bridging the gap between ecological diversity indices and measures of biodiversity and Allen et al. [32] used a related, unconstrained, form of weighted entropy under the scope of phylogenetic measures.
The work presented here has some similarity with a decision aiding procedure based on expected utility and Shannon entropy [33] , though here we use weighted entropy. The objectives of this paper include proving and discussing the mathematical properties of the optimal solution and providing a critical analysis of an expected utility and weighted entropy framework (EU-WE) as a conceptual device generating relative compositional scenarios of mosaics based on optimality criteria.
2. Methodology
In what follows a new set of the results and proofs are presented, equivalent, but different, from those presented before, e.g., [25] , now indexed to the optimal value of the Lagrange multiplier, which allows for an insightful interpretation, anchoring the optimal solution of this EU-WE framework with weighted entropy.
2.1. Index KU
We will be dealing with proportions, defining a normalized measure space. Proportions are relative extension measures—as well as relative frequencies and probabilities—the difference is that proportions reflect the extension of actual, or presumably effective, states of a system, and probabilities are possibility measures of events compatible with Kolmogorov’s axiomatic definition. Nevertheless, the two concepts are intimately linked under the scope of objective or physical probabilities, which often uses probability practically as a synonym for proportion [34] . Anscombe and Aumann [35] pointed out that physical probabilities can be determined empirically by noting the proportion of successes in some trials. Either as proportions, relative frequencies, or probabilities, these real numbers denote the same mathematical object, a simplex, with different connotations or semantic injunctions, depending on the context.
Assume that a system is characterized by a scenario of the world defined as the set of n elementary states, or sample space: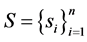 ; also assume that
; also assume that 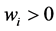 is a real positive number denoting a characteristic value of the state of the system applying the injective function
is a real positive number denoting a characteristic value of the state of the system applying the injective function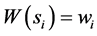 ; the power set
; the power set 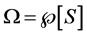 is the set of events, members of the collection generated by S; elementary states occur linked to the discrete distribution denoted as
is the set of events, members of the collection generated by S; elementary states occur linked to the discrete distribution denoted as 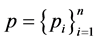 with
with 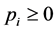 and
and 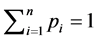 defining a
defining a ![]() simplex. The structure
simplex. The structure 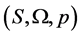 is a normalized measure space, with the condition
is a normalized measure space, with the condition 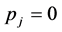 meaning the absence of the indexed j state.
meaning the absence of the indexed j state.
Next we outline an information based family of utility functions: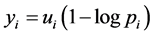 for
for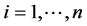 ; symbol U defines a monotone increasing transformation of the original characteristic values such as
; symbol U defines a monotone increasing transformation of the original characteristic values such as 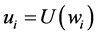 with
with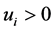 . We can assign proportions or probabilities
. We can assign proportions or probabilities 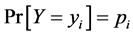 for
for 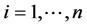 and the utility functions here defined are the product of utilities and context values,
and the utility functions here defined are the product of utilities and context values, 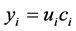 where the context value is expressed by
where the context value is expressed by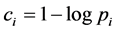 with range
with range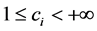 , and the term
, and the term 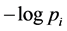 is the information value relative to elementary state i. Context values
is the information value relative to elementary state i. Context values 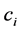 increase with correspondent information values, meaning that scarcity is considered as if it entails more relevance, which is the case, for instance, with the methodology outlined by Haddock et al. [36] , where the use of scarcity weights to assess impacts in landscape changes reflect the analogy that “endangered habitats” have a similar status of endangered species.
increase with correspondent information values, meaning that scarcity is considered as if it entails more relevance, which is the case, for instance, with the methodology outlined by Haddock et al. [36] , where the use of scarcity weights to assess impacts in landscape changes reflect the analogy that “endangered habitats” have a similar status of endangered species.
The EU-WE framework here to be discussed, denoted index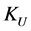 , is then defined using the expected value operator
, is then defined using the expected value operator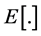 , evaluating the weighted average of the values
, evaluating the weighted average of the values , with the suitable decomposition
, with the suitable decomposition
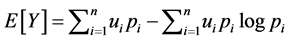 rewritten in Equation (1) as
rewritten in Equation (1) as
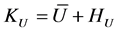 (1)
(1)
where 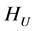 means the weighted entropy of the utilities
means the weighted entropy of the utilities 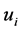 and
and ![]() is traditional expected utility. Obviously, denoting
is traditional expected utility. Obviously, denoting 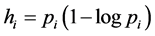 we may rewrite (1) as
we may rewrite (1) as 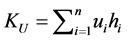 which may be interpreted as a nonlinearexpected utility because the terms
which may be interpreted as a nonlinearexpected utility because the terms 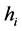 aren’t additive proportions or probabilities: although they verify the unitary hypercube condition, as we have that
aren’t additive proportions or probabilities: although they verify the unitary hypercube condition, as we have that 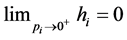 thus allowing for the extension
thus allowing for the extension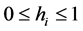 , we also see that the sum
, we also see that the sum 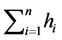 equates
equates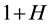 , with
, with 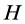 denoting Shannon entropy.
denoting Shannon entropy.
2.2. Optimal Proportions and Maximum Value of Index KU
Building auxiliary Lagrange function defined as 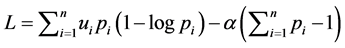 we can find the partial derivatives evaluated as
we can find the partial derivatives evaluated as 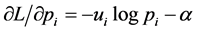 for
for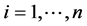 , from what follows, solving the equations
, from what follows, solving the equations
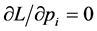 , the results:
, the results: 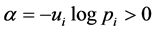 if
if 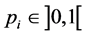 and
and 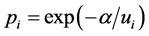 with the closure condition
with the closure condition
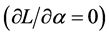 re-expressed as
re-expressed as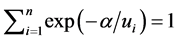 .
.
The numeric solution of this equation will be denoted 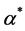 and we can prove it is unique, following a corollary of Bolzano theorem. If we define
and we can prove it is unique, following a corollary of Bolzano theorem. If we define 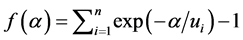 we observe that
we observe that 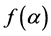 has a strictly negative derivative computed as
has a strictly negative derivative computed as  hence
hence 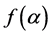 is strictly decreasing; the following calculus of limits confirm the existence and the uniqueness of the solution:
is strictly decreasing; the following calculus of limits confirm the existence and the uniqueness of the solution: 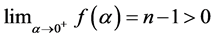
if ![]() and
and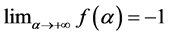 , so there is only one real value such that
, so there is only one real value such that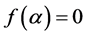 .
.
Thus, the critical point of index 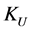 has coordinates defined by (2):
has coordinates defined by (2):
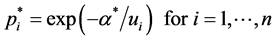 (2)
(2)
As expression (2) depends on the value of 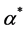 first we have to solve numerically the equation that defines the closure condition in the simplex, what implies solving Equation (3) for
first we have to solve numerically the equation that defines the closure condition in the simplex, what implies solving Equation (3) for 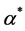
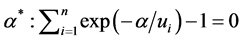 (3)
(3)
It can also be proven that each optimal coordinate 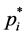 increases with the correspondent characteristic value, or utility, and decreases when the other utilities increase [26] [27] , as it should be expectable, lying within the open interval
increases with the correspondent characteristic value, or utility, and decreases when the other utilities increase [26] [27] , as it should be expectable, lying within the open interval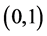 .
.
Next, let us prove that the critical point is a maximum in analogy with Guiasu procedure [17] . We build the auxiliary function 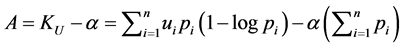 and rearrange the terms obtaining the sequence of equalities:
and rearrange the terms obtaining the sequence of equalities:
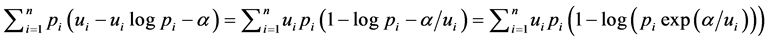
and eventually get the equivalent mathematical expression for the auxiliary function
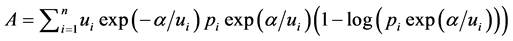 .
.
Using the auxiliary result 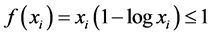 if
if 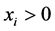 we have that the maximum point is located at
we have that the maximum point is located at 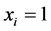 with the maximum value becoming
with the maximum value becoming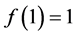 ; then, replacing
; then, replacing 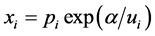 we conclude that inequality
we conclude that inequality 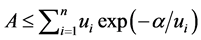 holds, and the maximum value is
holds, and the maximum value is 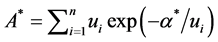 which is reached if and only if we have the replacement
which is reached if and only if we have the replacement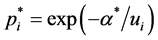 , thus verifying the result (2) as the maximum point coordinates.
, thus verifying the result (2) as the maximum point coordinates.
2.3. The Optimal Value of the Lagrange Multiplier of Index KU
Retrieving auxiliary function 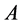 we can rewrite:
we can rewrite: 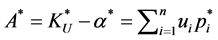 and the optimal value of the Lagrange multiplier evaluates as
and the optimal value of the Lagrange multiplier evaluates as  entailing the result:
entailing the result:
 (4)
(4)
Formula (4) is the weighted entropy of the optimal solution of index 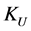 defined as
defined as 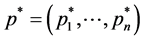 evaluated by Formula (2) after numerical evaluation of Equation (3); note that this is not to be confused with the maximum point of weighted entropy itself.
evaluated by Formula (2) after numerical evaluation of Equation (3); note that this is not to be confused with the maximum point of weighted entropy itself.
Optimal proportions are indifferent to a linear positive transformation in the utilities, such as a change of scale or units of measure. In particular, if we replace the utilities 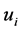 by its normalized (and dimensionless) form
by its normalized (and dimensionless) form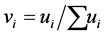 —acknowledging that the
—acknowledging that the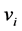 ’s are intrinsically merged within another simplex—the optimal solutions
’s are intrinsically merged within another simplex—the optimal solutions 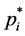 are the same as those evaluated with the original utilities
are the same as those evaluated with the original utilities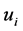 , and the optimal Lagrange multiplier value becomes also normalized as
, and the optimal Lagrange multiplier value becomes also normalized as![]() .
.
2.4. Range of Index KU
The minimum value of index 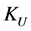 is
is 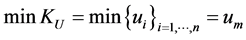 which is a straightforward result because weighted entropy verifies
which is a straightforward result because weighted entropy verifies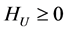 ; as
; as 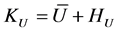 defined in (1) the second term of the sum vanishes at the vertexes of the simplex and the first term takes the minimum value when
defined in (1) the second term of the sum vanishes at the vertexes of the simplex and the first term takes the minimum value when 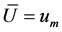 so the result holds. The maximum value of the index
so the result holds. The maximum value of the index 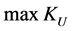 may be calculated with optimal proportions by direct substitution as
may be calculated with optimal proportions by direct substitution as
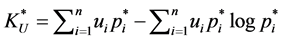 or, equivalently, indexed to the optimal value of the Lagrange multiplier evaluated in (3), obtaining the expression
or, equivalently, indexed to the optimal value of the Lagrange multiplier evaluated in (3), obtaining the expression
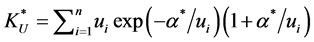 (5)
(5)
Thus, since  is a continuous function in the proportions
is a continuous function in the proportions , defined in a compact set—the simplex—we have the general result, following Bolzano-Weierstrass theorem, concerning the range of the EU-WE here discussed:
, defined in a compact set—the simplex—we have the general result, following Bolzano-Weierstrass theorem, concerning the range of the EU-WE here discussed: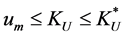 , the last term of the double inequality referred to in Equation (5).
, the last term of the double inequality referred to in Equation (5).
2.5. Exemplification
As an example, we retrieve characteristic economic values of forest habitats from [27] and exemplify the use of the formulas presented in this paper. In the case, we have 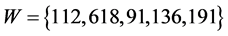 and with neutral utilities of the form
and with neutral utilities of the form 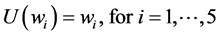 we obtain for Equation (3) the following expression:
we obtain for Equation (3) the following expression:
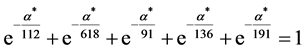 which solved numerically for
which solved numerically for 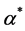 gives the value
gives the value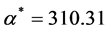 . Then, applying Formula (2), rounding up to three decimals, we get:
. Then, applying Formula (2), rounding up to three decimals, we get: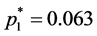 ;
;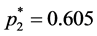 ;
;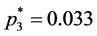 ;
; 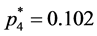 and
and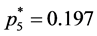 .
.
Using these optimal values and evaluating Formula (4) we obtain 310. 43 which is quite similar to the value of 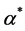 evaluated numerically, except for the influence of small rounding errors, thus confirming that the optimal value of the Lagrange multiplier is the weighted entropy of the optimal point of index
evaluated numerically, except for the influence of small rounding errors, thus confirming that the optimal value of the Lagrange multiplier is the weighted entropy of the optimal point of index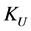 . Finally, computing (5) we get the maximum value of the index:
. Finally, computing (5) we get the maximum value of the index: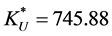 .
.
Other utilities could have been used besides the neutral, either convex, risk-taking utilities, as it would be the case with 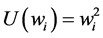 or concave, risk-averting utilities, such as
or concave, risk-averting utilities, such as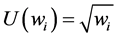 ; the first type would promote the proportions related to higher characteristic values penalizing the remnant, and the second type, on the contrary, would enhance a more balanced optimal composition solution.
; the first type would promote the proportions related to higher characteristic values penalizing the remnant, and the second type, on the contrary, would enhance a more balanced optimal composition solution.
3. Discussion
The EU-WE framework here discussed emphasizes the notion of contributive value of each component of a mosaic—or stable state of a simultaneous multi-state system—depending both on context and utility values. Others seem to identify contributive value with utility itself (see [37] ), which is not the case here, where traditional expected utility is balanced by the weighted entropy of the utilities. We remark that weighted entropy—or related forms of Shannon entropy—though it has already a long history of almost half a century since its first reference [16] , is yet being referred to as a risk measure in portfolio selection strategies (e.g. [38] [39] ).
The static nonlinear optimization procedure presented here may be applied with focus on compositional scenarios generated under active adaptive ecosystem management paradigm sensu Gunderson et al. [40] , a reinforcement process, or as a dynamic system: if the characteristic values, or the correspondent utilities, change in time, so will change the optimal proportions, addressing the issue of whether the mosaic will after some time converge to a steady state or be continuously changing (see [41] ). Clark et al. [42] point out that utility analysis has been used in environmental policy design studies to help articulate conflicting experiences and simplify comparisons of policies, though it is also useful remember that the precautionary principle advises that resilience of an ecosystem may be lost because of activities that focus on an optimal control strategy of a single target variable [43] . Last, let us recall that decision analysis concerns with the balancing of factors that influence a decision, in a procedure that incorporates uncertainties, values, and preferences, in a basic structure that models the decision [44] , and recently it was proposed a semiotic interpretation of weighted entropy as mean contextual relevance of events indexed to a sample space and a context of utility [45] .
References
- Guiasu, R.C. and Guiasu, S. (2010) The Rich-Gini-Simpson Quadratic Index of Biodiversity. Natural Science, 2, 1130-1137. http://dx.doi.org/10.4236/ns.2010.210140
- Guiasu, R.C. and Guiasu, S. (2011) The Weighted Quadratic Index of Biodiversity for Pairs of Species: A Generalization of Rao’s Index. Natural Science, 3, 795-801. http://dx.doi.org/10.4236/ns.2011.39104
- Forman, R.T.T. (1995) Land Mosaics—The Ecology of Landscapes and Regions. Cambridge University Press, Cambridge.
- Rocchini, D. (2005) Resolution Problems in Calculating Landscape Metrics. Journal of Spatial Science, 50, 25-35. http://dx.doi.org/10.1080/14498596.2005.9635047
- Uuemaa, E., Antrop, M., Roosaare, J., Marja, R. and Mander, U. (2009) Landscape Metrics and Indices: An Overview of Their Use in Landscape Research. Living Reviews in Landscape Research, 3, 1-28. http://dx.doi.org/10.12942/lrlr-2009-1
- Nagendra, H. (2002) Opposite Trends in Response for the Shannon and Simpson Indices of Landscape Diversity. Applied Geography, 22, 175-186. http://dx.doi.org/10.1016/S0143-6228(02)00002-4
- Bernardo, J.M. (1979) Expected Information as Expected Utility. The Annals of Statistics, 7, 686-690. http://dx.doi.org/10.1214/aos/1176344689
- Shannon, C.E. (1948) A Mathematical Theory of Communication. Bell System Technical Journal, 27, 379-423, 623-656. http://cm.bell-labs.com/cm/ms/what/shannonday/shannon1948.pdf http://dx.doi.org/10.1002/j.1538-7305.1948.tb01338.x
- Hartley, R.V.L. (1928) Transmission of Information. Bell System Technical Journal, 7, 535-563. http://dotrose.com/etext/90_Miscellaneous/transmission_of_information_1928b.pdf
- Jaynes, E.T. (1957) Information Theory and Statistical Mechanics. The Physical Review, 106, 620-630. http://dx.doi.org/10.1103/PhysRev.106.620
- Kornreich, P. (2008) Mathematical Models of Information and Stochastic Systems. CRC Press, Boca Raton. http://dx.doi.org/10.1201/b15825
- Klir, G.J. (2006) Uncertainty and Information: Foundations of Generalized Information Theory. John Wiley & Sons, New Jersey.
- Rènyi, A. (1961) On Measures of Entropy and Information. Proceedings of the 4th Berkeley Symposium on Mathematical Statistics and Probability, 547-561. http://projecteuclid.org/euclid.bsmsp/1200512181
- Ricotta, C., Corona, P., Marchetti, M., Chirici, G. and Innamorati, S. (2003) LaDy: Software for Assessing Local Landscape Diversity Profiles of Raster Land Cover Maps Using Geographic Windows. Environmental Modelling & Software, 18, 373-378. http://dx.doi.org/10.1016/S1364-8152(02)00104-4
- Hill, M.O. (1973) Diversity and Evenness: A Unifying Notation and Its Consequences. Ecology, 54, 427-432. http://dx.doi.org/10.2307/1934352
- Bellis, M. and Guiasu, S. (1968) A Quantitative-Qualitative Measure of Information in Cybernetic Systems. IEEE Transactions on Information Theory, 14, 593-594. http://dx.doi.org/10.1109/TIT.1968.1054185
- Guiasu, S. (1971) Weighted Entropy. Reports on Mathematical Physics, 2, 165-179. http://dx.doi.org/10.1016/0034-4877(71)90002-4
- Guiasu, S. (1986) Grouping Data by Using the Weighted Entropy. Journal of Statistical Planning and Inference, 15, 63-69. http://dx.doi.org/10.1016/0378-3758(86)90085-6
- Aggarwal, N.L. and Picard, C.-F. (1978) Functional Equations and Information Measures with Preference. Kybernetika, 14, 174-181. http://dml.cz/dmlcz/125412
- Batty, M. (1986) Cost, Accessibility and Weighted Entropy. Geographical Analysis, 15, 256-267. http://dx.doi.org/10.1111/j.1538-4632.1983.tb00786.x
- Nawrocki, D.N. and Harding, W.H. (1986) State-Value Weighted Entropy as a Measure of Investment Risk. Applied Economics, 18, 411-419. http://dx.doi.org/10.1080/00036848600000038
- Taneja, H.C. and Tuteja, R.K. (1986) Characterization of a Quantitative-Qualitative Measure of Inaccuracy. Kybernetika, 22, 393-402. http://dml.cz/dmlcz/124578
- Guiasu, R.C. and Guiasu, S. (2003) Conditional and Weighted Measures of Ecological Diversity. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 11, 283-300. http://dx.doi.org/10.1142/S0218488503002089
- Guiasu, R.C. and Guiasu, S. (2012) The Weighted Gini-Simpson Index: Revitalizing an Old Index of Biodiversity. International Journal of Ecology, 2012, Article ID: 478728. http://dx.doi.org/10.1155/2012/478728
- Casquilho, J., Neves, M. and Rego, F. (1997) Extensões da Função de Shannon e Equilíbrio de Proporções-Uma Aplicação ao Mosaico de Paisagem. Anais do Instituto Superior de Agronomia, 46, 77-99. http://hdl.handle.net/10400.5/4725
- Casquilho, J.A.P. (1999) Ecomosaico: Índices para o Diagnóstico de Proporções de Composição. Ph.D. Thesis, Instituto Superior de Agronomia, Universidade Técnica de Lisboa, Lisboa. http://hdl.handle.net/10068/330947
- Casquilho, J.P (2010) Landscape Mosaic Composition and Mean Contributive Value Index. Silva Lusitana, 18, 197- 203. http://www.scielo.oces.mctes.pt/pdf/slu/v18n2/v18n2a06.pdf
- Casquilho, J.A.P. (2012) Ecomosaico Florestal: Composição, Índices de Informação e Abdução. Revista Árvore, 36, 321-329. http://dx.doi.org/10.1590/S0100-67622012000200013
- Stratton-Lake, P. (2004) Kant, Duty, and Moral Worth. Routledge, New York.
- Arrhenius, G. and Rabinowicz, W. (2005) Value and Unacceptable risk. Economics and Philosophy, 21, 177-197. http://dx.doi.org/10.1017/S0266267105000556
- Ricotta, C. (2002) Bridging the Gap between Ecological Diversity Indices and Measures of Biodiversity with Shannon’s Entropy: Comment to Izsák and Papp. Ecological Modelling, 152, 1-3. http://dx.doi.org/10.1016/S0304-3800(01)00468-9
- Allen, B., Kon, M. and Bar-Yam, Y. (2009) A New Phylogenetic Diversity Measure Generalizing the Shannon Index and Its Application to Phyllostomid Bats. The American Naturalist, 174, 236-243. http://dx.doi.org/10.1086/600101
- Yang, J. and Qiu, W. (2005) A Measure of Risk and a Decision-Making Model Based on Expected Utility and Entropy. European Journal of Operational Research, 164, 792-799. http://dx.doi.org/10.1016/j.ejor.2004.01.031
- Ramsey, F.P. (1931) Truth and Probability. In: Braithwaite, R.B., Ed., The Foundations of Mathematics and other Logical Essays, Harcourt, Brace and Company, New York, 156-198.
- Anscombe, F.J. and Aumann, R.J. (1963) A Definition of Subjective Probability. The Annals of Mathematical Statistics, 34, 199-205. http://www.jstor.org/stable/2991295 http://dx.doi.org/10.1214/aoms/1177704255
- Haddock, J., Tzanopoulos, J., Mitchley, J. and Fraser, R. (2007) A Method for Evaluating Alternative Landscape Managementscenarios in Relation to the Biodiversity Conservation of Habitats. Ecological Economics, 61, 277-283. http://dx.doi.org/10.1016/j.ecolecon.2006.02.019
- Oral, M. (2012) Action Research Contextualizes DEA in a Multi-Organizational Decision-Making Process. Expert Systems with Applications, 39, 6503-6513. http://dx.doi.org/10.1016/j.eswa.2011.12.054
- Bhattacharyya, R., Chatterjee, A. and Kar, S. (2013) Uncertainty Theory-Based Multiple Objective Mean-Entropy- Skewness Stock Portfolio Selection Model with Transaction Costs. Uncertainty Analysis and Applications, 1, 16. http://dx.doi.org/10.1186/2195-5468-1-16
- Ormos, M. and Zibriczky, D. (2013) Asset Pricing and Entropy. European Financial Systems 2013 Deev. Proceedings of the 10th International Scientific Conference, Masaryk University, Brno, 2013, 241-248. http://is.muni.cz/do/econ/soubory/konference/efs/Sbornik_2013.pdf#page=241
- Gunderson, L.H., Holling, C.S. and Allen, C.R. (2010) Conclusion: The Evolution of an Idea-the Past, Present, and Future of Ecological Resilience. In: Gunderson, L.H., Allen, C.R. and Holling, C.S., Eds., Foundations of Ecological Resilience. Island Press, Washington DC, 423-444.
- Hubacek, K. and Van Den Bergh, J.C.J.M. (2006) Changing Concepts of Land in Economic Theory: From Single to Multi-Disciplinary Approaches. Ecological Economics, 56, 5-27. http://dx.doi.org/10.1016/j.ecolecon.2005.03.033
- Clark, W.C., Jones, D.D. and Holling, C.S. (2010) Lessons for Ecological Policy Design: A Case Study of Ecosystem Management. In: Gunderson, L.H., Allen, C.R. and Holling, C.S., Eds., Foundations of Ecological Resilience, Island Press, Washington DC, 331-394.
- Allen, C.R., Gunderson, L.H. and Holling, C.S. (2010) Commentary on Part Three Articles. In: Gunderson, L.H., Allen, C.R. and Holling, C.S., Eds., Foundations of Ecological Resilience, Island Press, Washington DC, 301-307.
- Howard, R.A. (2008) The Foundations of Decision Analysis Revisited. In: Edwards, W., Milles Jr., R.F. and von Winterfeldt, D., Eds., Advances in Decision Analysis—From Foundations to Applications, Cambridge University Press, Cambridge, 32-56.
- Casquilho, J.P. (2013) Informação Útil ou Entropia Ponderada: Revisão e Desenvolvimentos. Revista Veritas, 1, 87-103. http://hdl.handle.net/10400.5/6598

