Natural Science
Vol.5 No.1(2013), Article ID:26633,9 pages DOI:10.4236/ns.2013.51011
Effects of life-history components on population dynamics of the rare endangered plant Davidia involucrata
![]()
1Department of City and Environment, Jiangsu Normal University, Xuzhou, China; *Corresponding Author: haimeiyou@jsnu.edu.cn
2Key Laboratory for Silviculture and Conservation of Ministry of Education and Beijing, Beijing Forestry University, Beijing, China
3Yokohama City University, Graduate School in Nanobioscience, Endowed Laboratory for Restoration of Terrestrial Environments, Yokohama, Japan
Received 20 November 2012; revised 21 December 2012; accepted 8 January 2013
Keywords: Davidia involucrata; Lefkovitch Matrix model; Life-History Stage; Population Ecology; Sensitivity Analysis
ABSTRACT
In order to estimate the most effect stage and process on population growth and effective conserve the rare endangered plant Davidia involucrata, we analyzed the dynamics and the contributions of life-history components on population dynamics based on Lefkovitch matrix model and sensitivity analysis. The life cycle of Davidia involucrata was divided into six stages (seed, seedling, juvenile, immature, early adult and late adult) based on the species characteristics and published literature data, the survival rates in each life-history stage were simulated using a static life table, and the fecundity of each stage was determined according to sample information. The results showed that the structure of the observed population was not ideal, and the numbers of seedlings and coppice shoots was similar. The population growth rate was influenced largely by individual growth process, and asexual reproduction made a larger contribution to population growth than sexual reproduction. However, sexual reproduction was more important than asexual reproduction, because most asexual reproducing individuals (the coppice shoots) were derived mainly from human destruction (e.g. felling trees). The most important stage was stage V (late adult), associated with seed production and germination. Therefore, conservation of Davidia involucrata populations should focus on stage V and sexual reproduction, in order to improve the seed production and germination rate, and to promote population stability and development.
1. INTRODUCTION
Davidia involucrata is a deciduous broad-leaved tree species belonging to the monotypic family Davidiaceae [1]. The species developed from the late Cretaceous to the Tertiary period; it occurred widely in many areas of the world in the late Tertiary but disappeared from many places during the Quaternary [2,3]. Davidia involucrata survives now only in several provinces of China (Sichuan, Hubei, Hunan, Guizhou, Yunnan, Gansu, Shaanxi and Chongqing city), which were influenced only weakly by the Quaternary glaciations [4-8]. Consequently, as a Tertiary relic, Davidia involucrata is also called a “botanic living fossil” and is rated as a first-class protected plant in China [9]. As their natural habitats were destoryed continually by human activities, however, the number of natural populations and the distribution area of this ancient plant have been decreasing remarkably. The survival of this rare species Davidia involucrata is facing severe challenges [10,11].
In order to conserve this rare endangered species, much research on Davidia involucrata has been carried out in fields including anatomy, genetics, biology, ecology, and the cultivation of introduced species [7,11-13]. Likewise, many studies on the population ecology of Davidia involucrata have been reported in the past 30 years. These studies involved population structure and spatial distribution patterns [14-19]; interspecific and intraspecific relationships [20-24]; population dynamics [25-27]; endangerment causes and protection [28,29], and other aspects. To date, however, studies on the population ecology of Davidia involucrata have been confined to macroscopic aspects and have neglected systematic analysis. Reports on the population dynamics of Davidia involucrata are especially scarce, and the endangerment mechanism of Davidia involucrata is not clear [7,11,12].
Population dynamics has consequences for the conservation of rare species [30-35]. Matrix models for structured populations, introduced by Leslie [36,37], is frequently used by ecologists to analyze population dynamics because they link individual growth rates to population processes and can be used easily to handle the complexity of plant life cycles [38]. Stage-structured matrix models, which were rediscovered and improved by Lefkovitch [39], are important analytical and theoretical tools for the study of population dynamics because these models may be appropriate for populations in which individual survival, growth, and reproduction are not linked directly to age, or in which the age of individuals is difficult to determine [40-43]. The demographic sensitivity of a population can provide a clear, straightforward ranking of the importance of different demographic rates and can identify the life-history stage that has the greatest impact on population dynamics [44-48]. The combination of the two analytical approaches may be useful to managers interested in identifying the most important life stages for species conservation [11,38].
In this paper we estimated the population dynamics of the rare endangered tree Davidia involucrate, based on a stage-structured matrix model; compared the potential effects of each stage population on whole population growth, for a given population; and then searched for the life-history stage that has the greatest impact on population dynamics, using demographic sensitivity analysis. Our goal was to find an approach for conserving the relic endangered plants effectively.
2. MATERIALS AND METHODS
2.1. Species Description
Davidia involucrata is a deciduous broad-leaved tree species with a height of 15 - 25 m, occurring naturally only in China. The individuals grow from the last ten days of February to the first ten days of October; they bloom over a period of 40 - 50 days, from the last ten days of April through May. Davidia involucrata regenerates mainly from seeds but also from vegetative buds (coppice shoots). The fruits are oval drupes with a diameter of 3 - 5 cm, which ripen in the last ten days of October. Each fruit contains one to six seeds, which maturate completely in two years. Before the age of 10, Davidia involucrata does not have an obvious taproot and branch roots. It begins to bloom when it is 6 - 8 years old and to fruit at age 10 - 15, with a fruiting peak at age 30 - 90 [2,9,20,49,50].
2.2. Data Collection
Estimating population dynamics based on a structured matrix model involves demographic parameters for each life stage, such as seed production, seed fate, individual survival, growth, etc. These data are difficult to obtain in a short term. Here we applied data from published literature, especially the data set investigated by Su et al. [51] in the Wolong nature reserve in Sichuan province, because this data set included all parameters relevant to the life stages of Davidia involucrata. We picked out 10 plots from the data set, each with at least five Davidia involucrata individuals. Other research results [29,51], on growth and reproduction of Davidia involucrata, were also used.
2.3. Stage Classification
There are few vegetative individuals in natural populations of Davidia involucrata, and the age distribution of these individuals is uneven. Here, we only classified the life-history stages roughly, based on biological characteristics and the dimensions of individuals, mainly DBH (diameter at breast height) and height. According to the standards introduced by Qu [52], the life history of Davidia involucrata was classified into six stages: seed; seedling (stage I, height < 33 cm); juvenile (stage II, height > 33 cm but DBH < 2.5 cm); immature (stage III, DBH between 2.5 cm and 7.5 cm); early adult (stage IV, DBH from 7.5 cm to 22.5 cm); and late adult (stage V, DBH > 22.5 cm). The numbers of Davidia involucrata trees in different life-history stages in each plot are shown in Table 1.
2.4. Stage Parameters
Davidia involucrata is a long-lived tree species with a complex life-history. The data obtained reflect only the specific structure of the population at a given time. To determine the demographic fates of vegetative (non-seed) individuals in different life stages, we compiled a life table of a Davidia involucrata population using the method of “space-for-time substitution” [53,54]. The observed numbers of vegetative individuals in each stage were justified based on the correlation between the average age of individuals and observed numbers in each life stage. The survival rates of vegetative individuals and the proportion of recruits in different life-history stages were calculated and are tabulated in Table 2. Furthermore, we assumed that all surviving individuals in stage i will transit into stage i + 1; thus, the recruitment in our study consists only of the coppice shoots.
Reproduction is an important process for population dynamics. The report on the relation between individual DBH and age shows that only those individuals belonging to stage IV and stage V have the ability to produce seeds [51]. We assume here that the mothers in these two stages have the same ability to produce seeds; thus, we

Table 1. Numbers of Davidia involucrata in each stage in the study plots (From Su et al. [51]).
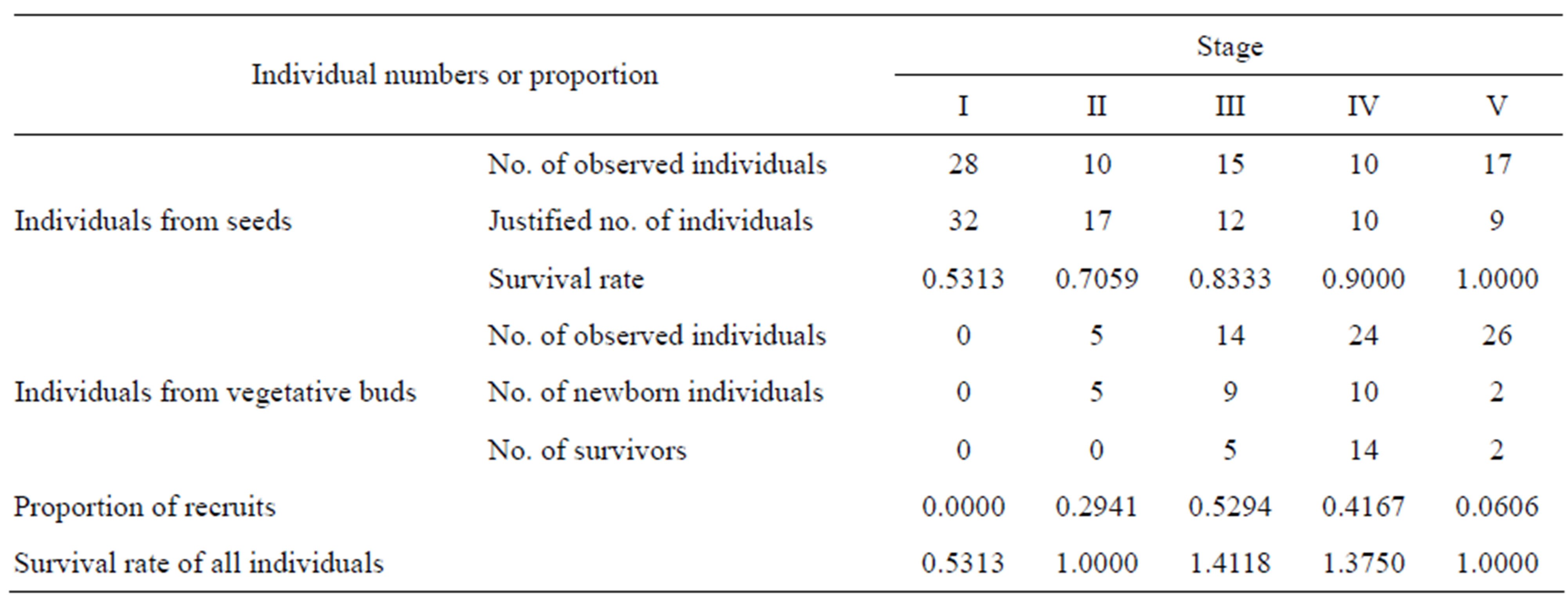
Table 2. Numbers and proportion of individuals by seeds and by vegetative buds in each stage.
obtained the average seed reproduction rate for both stages according to the data of Su et al. [51], where 91 individuals belonging to the two stages produced 1333 seeds. On the other hand, Davidia involucrata may also produce offspring by asexual reproduction. The proportions of newborn coppice shoots in different stages can be derived by calculating the percentages of new sprouts in the same stage (Table 2).
The fate of seeds of Davidia involucrata in the study area was also reported by Su et al. [51], suggesting that the maximum seed germination rate reached 2.1% and the average seed germination rate was 1.01%.
2.5. Population Matrix Model
The matrix model of population structure can be represented by:
 (1)
(1)
where n (t) and n (t + 1) are the vectors of all the individuals in the population at time t and time t + 1, respectively. A is the stage-structured matrix, showing how individuals in each stage at one time may advance to other stages by the next time unit. This matrix is represented by:
 (2)
(2)
where Fi1 is the ability of sexual reproduction in stage i, and Pij is the probability that individuals in stage i transit into stage j.
To characterize the forest population dynamics, such a stage-structured matrix was assembled by weighting the observed transitions based on their frequency in the entire data set and by pooling all the observations of particular transition events over the whole data set. For our population, the summary matrix A is a 6 × 6 matrix, in which each entry aij refers to the contribution of individuals in stage i to stage j in the next time step. To ascertain the effect of seed germination rate and asexual reproduction on population dynamics, four matrices of dimension 6 × 6 were constructed, as follow:




Here, A1 and A2 represent the average stage-structured matrices of the overall population and the sexually reproductive population (not including individuals from vegetative shoots), with the average seed germination rate (1.01%); A3 and A4 are the maximum stage-structured matrices of the overall population and the sexually reproductive population at the maximum seed germination rate (2.10%).
The demographic properties of the population dynamics are determined by the eigenvalue of A, and the dominant eigenvalue of the matrix can be used to estimate population dynamics, due to the fact that it corresponds to the asymptotic population growth rate λ. The population will grow or decline (or remain stable) depending on whether λ is greater or less than (or equal to) one [43,55].
2.6. Demographic Sensitivity Analysis
Demographic sensitivity analysis includes sensitivity analysis and elasticity analysis. Sensitivity involves an index that measures how changes in individual life-history parameters influence the population growth rate [35, 56]. High sensitivity for a given transition means that small changes of a value in the matrix will have large effects on growth rate [57]:
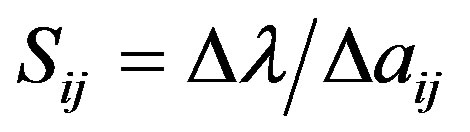 (3)
(3)
where Sij represents sensitivity, λ is the population growth rate, and ∆aij represents a small change of the matrix element aij. Here, ∆aij = 0.0001.
Elasticity is a measure of proportional sensitivity and measures the effects of proportionally scaled perturbations [58]. Elasticities are more readily comparable among stages than are sensitivities because they are already scaled by the magnitudes of the transitions themselves [35]. Elasticity (Eij) can be derived from:
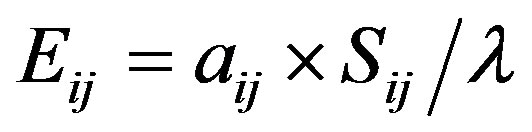 (4)
(4)
where ΣEij = 1.
3. RESULTS AND ANALYSIS
3.1. Population Dynamics
Vegetative individuals of Davidia involucrata are of two types, those from seeds (called sexually reproductive individuals) and those from vegetative shoots (called sprouts or coppice shoots). The numbers of both kinds of individuals in the forest population are similar, amounting to 53.69% for sexually reproductive individuals and 46.31% for individuals coppice shoots. Stage distribution patterns of the sexually reproductive individuals and coppice shoots were different, with total numbers decreasing first and then increasing over the life-history stages (Figure 1).
The dynamics of the Davidia involucrata population is related to the fates of both sexually reproductive individuals and coppice shoots. For the overall population, the dominant eigenvalue λ1 of the matrix A1 is 1.0452 (>1), indicating that the population would grow slowly. Nonetheless, when the coppice shoots were ignored, the
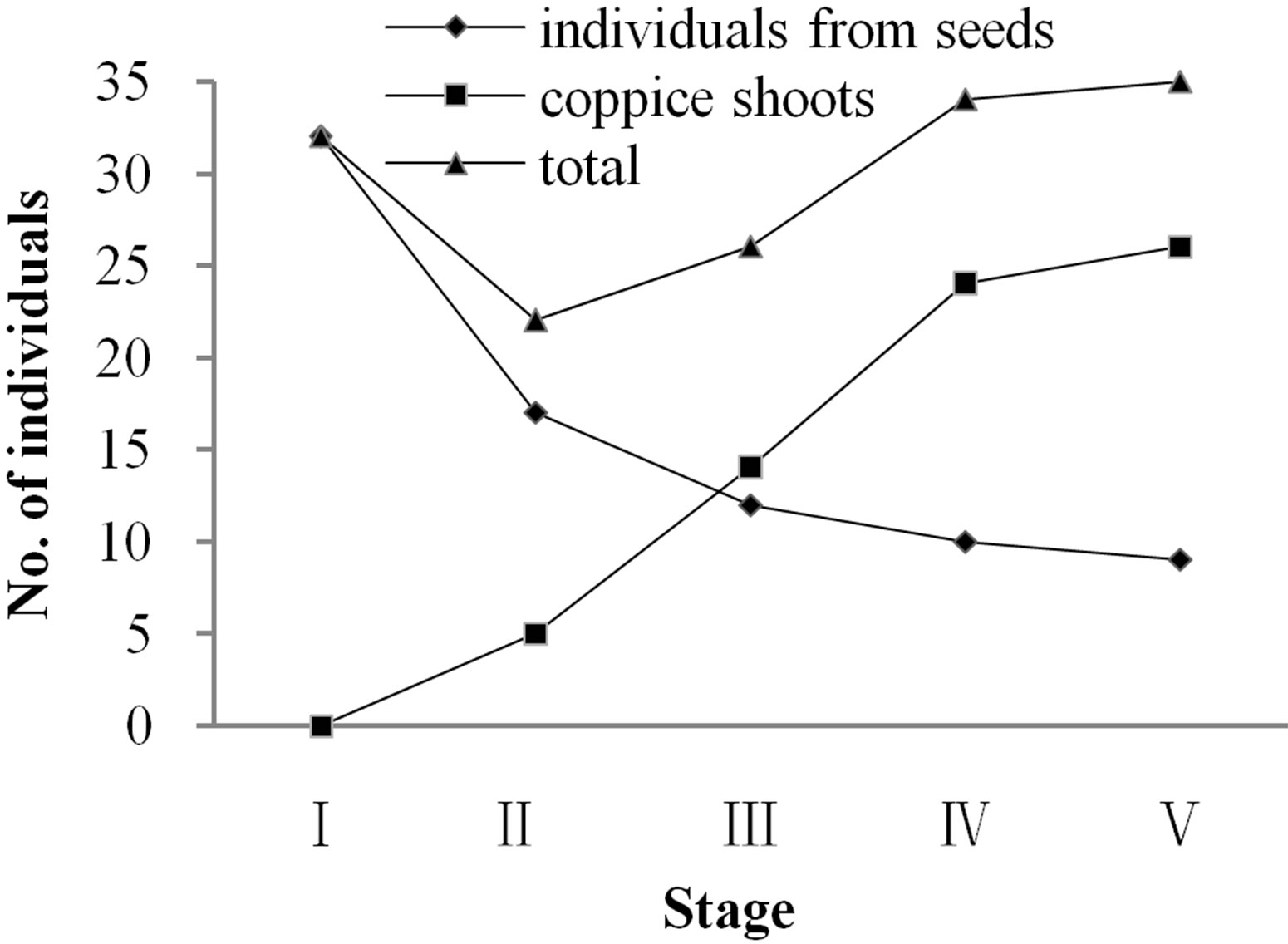
Figure 1. Distribution of population individuals in each life-history stage.
dominant eigenvalue of the population matrix A2, called λ2, is 0.6329 (<1), showing that the sexually reproductive population would decline fairly rapidly (Figure 2). So, coppice shoots increase population growth, and vegetative propagation is an important event of population growth.
Population dynamics is also associated with seed fates. For the overall population, the dominant eigenvalue of the matrix increased from λ1 = 1.0452 to λ3 = 1.1521 when the seed germination rate increased from the average value of 1.01% to the maximum value of 2.1% (Figure 2). This suggests that increasing the germination rate would increase population growth. Likewise, for the sexually reproductive population, the dominant eigenvalue of the matrix increased from λ2 = 0.6329 to λ4 = 0.7248 with the increased seed germination rate. Nevertheless, the growth rates of the sexually reproductive population, for the two kinds of seed germination, were less than 1, indicating that the sexually reproductive population would decline rapidly and even die out in nature due to lack of coppice shoots or asexual reproduction.
3.2. Demographic Sensitivity
Individuals of different stages contribute differently to population growth rate, and the sensitivity index provides a measure of the importance of the different lifehistory stages. In our study, sensitivities were calculated from summary models for both the overall population and the sexually reproductive population, in order to identify which life-history stage has the greatest effect on population growth. Sensitivity matrices for the overall population (S1) and sexually reproductive population (S2), with average seed germination rate, are as follow:


The largest sensitivities in both population matrices, in boldface, were for the seed germination rates (S12), indicating that population growth rate was most sensitive to rapid growth of newly germinated seedlings. Population
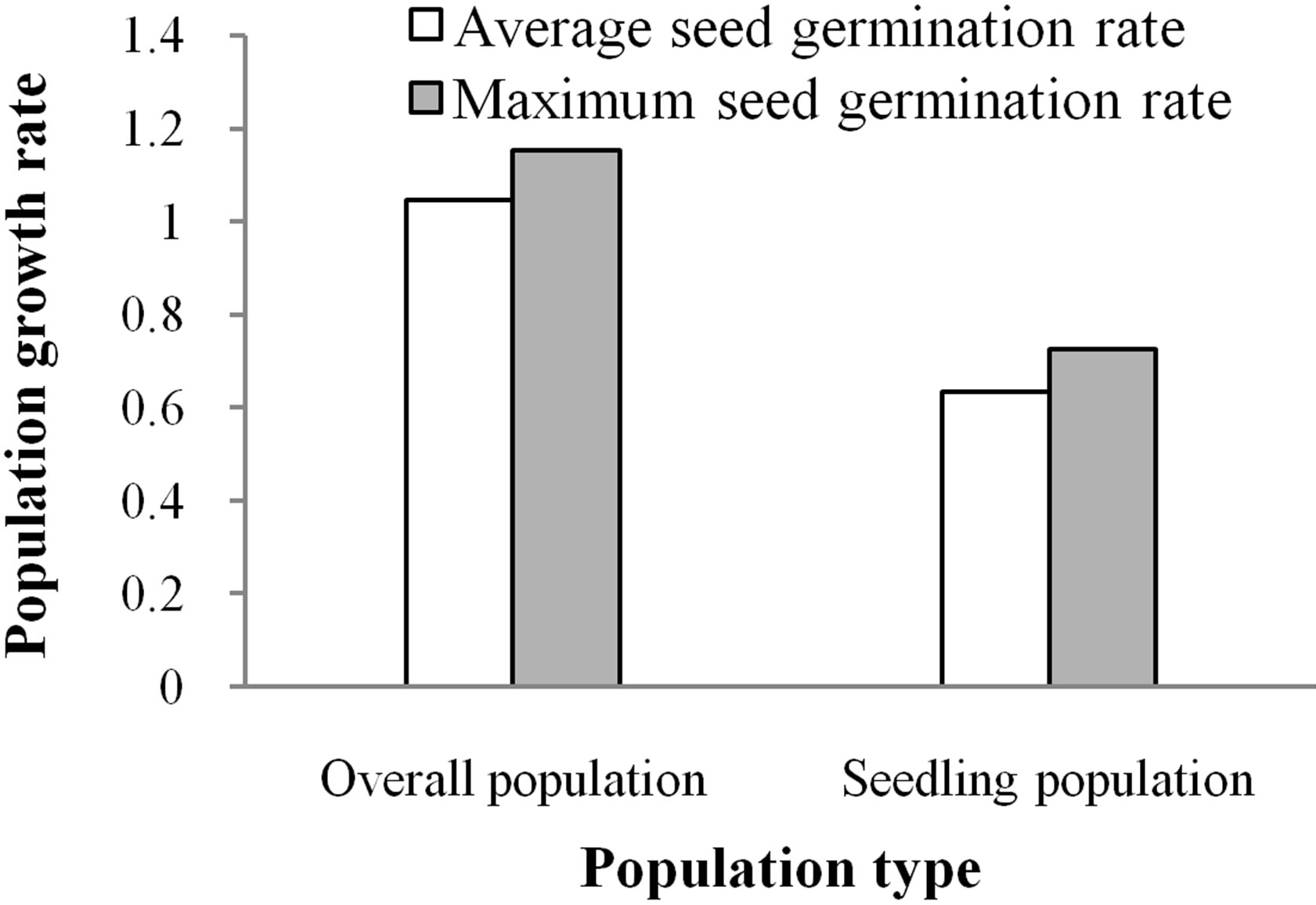
Figure 2. Population growth rates at different seed germination rates.
growth was less sensitive to changes in seed production (S41 and S51) than other parameters because the values for seed reproduction in the summary model are larger. However, the sensitivity for contributions to seeds was different in different stages, with population growth rate influenced more by stage V. Moreover, vegetative propagation (S33, S44 and S55) had a higher impact on population growth than did seed reproduction (S41 and S51) and a stage transitions by the coppice shoots (S34, S45 and S56).
Elasticity measures the proportional contribution of stage parameters to population growth. Total elasticities for each stage were calculated by summing the proportional contribution of each entry belonging to the same stage. For the overall population, stage III (0.2631) had the greatest total elasticity, and stage V (0.0803) had the smallest. This indicates that the total elasticity was evenly spread over all stages and that stage III was the most important stage for population growth (Table 3).
For the sexually reproductive population, the total elasticities for each stage varied from 0.1552 to 0.1868, implying that the relative importance of different lifehistory stages to population growth was similar. The greatest values for different life-history processes (growth and reproduction) were associated with seeds. In particular, the quantity and quality of seeds for stage V made the greatest contribution to the population dynamics (Table 4).
In order to compare the relative importance of different life-history processes to population growth, the total elasticity for each life-history process was calculated by summing the proportional contributions. For both the overall population and the sexually reproductive population, the total elasticity of the individual growth process was more than that of reproduction, and the total elasticity for sexual reproduction (0.1297) was relatively small compared to that asexual reproduction (0.2749).
In the elasticity matrix for the overall population, the entries with the greatest elasticity for each life-history
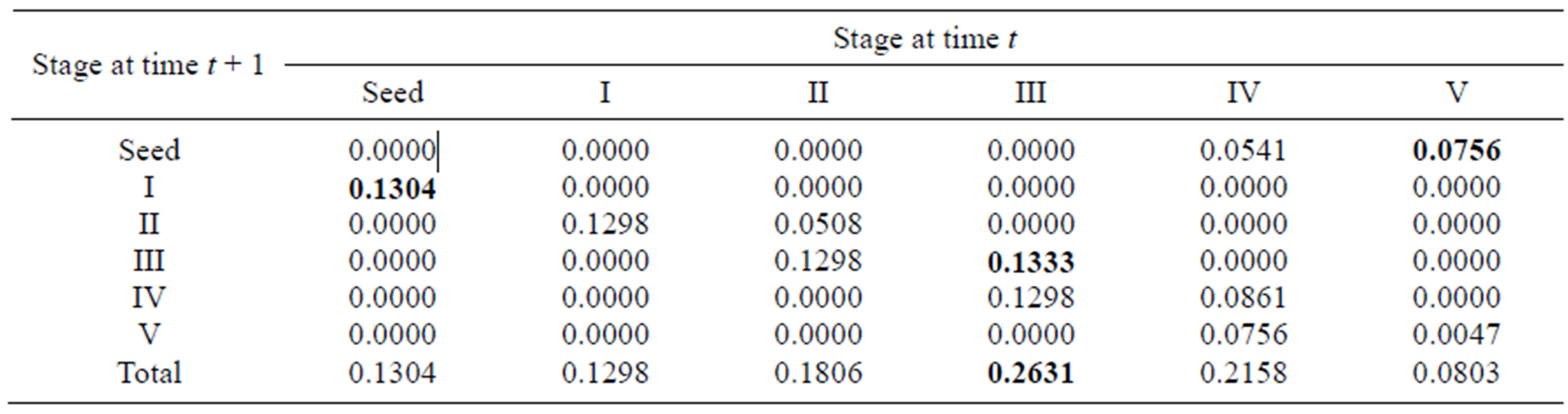
Table 3. Elasticity values for the summary matrix of the overall population; the largest elasticity values in different life-history processes are in boldface.
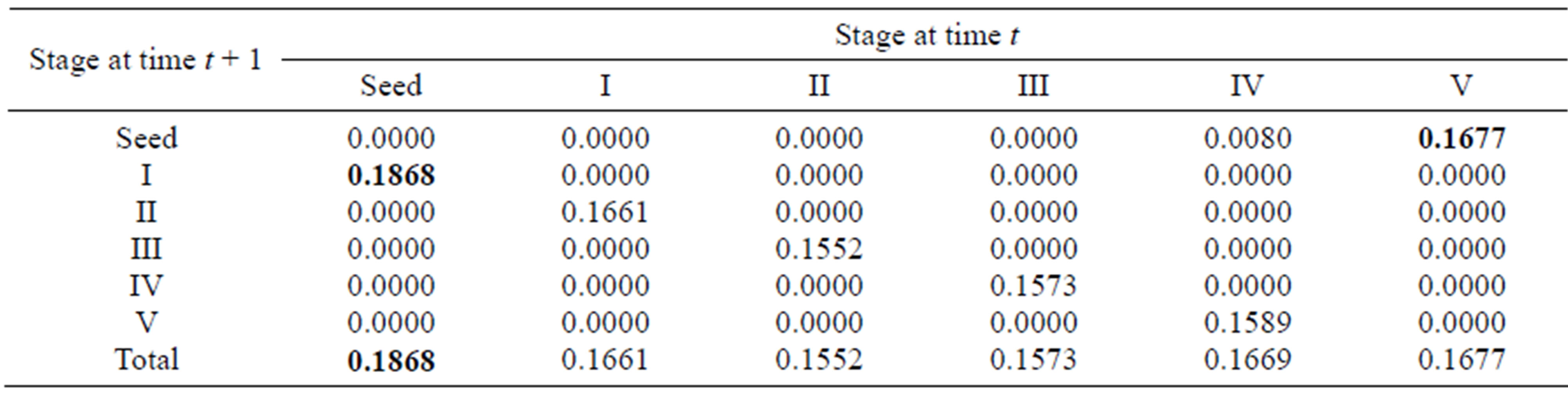
Table 4. Elasticity values for the summary matrix of the sexually reproductive population; the largest elasticity values in different life-history processes are in boldface.
process were the seed germination rate (0.1304) for growth, the proportion of recruits in stage III (0.1333) for survival (or vegetative propagation) and the seed production rate of stage V (0.0756) for sexual reproduction. These entries with greatest elasticity involved the seed stage, stage III and stage V. Also, because the seed germination rates are also correlated with their quality and quantity (affected by the mother plants), the above three entries with greatest elasticity for different life-history processes were associated with producing seeds and sprouts, showing that reproduction is the most important process for population growth. In addition, the growth parameters in the four early stages (from seed to stage III) had larger elasticity values than the other stages, suggesting that the behavior of the individuals in the first three stages had the largest impact on population growth. Similarly, for the sexually reproductive population, the matrix entries with greatest elasticity for each life-history process were the seed germination rate for growth and seed production rate in stage V for reproduction, indicating that stage V had the most important effects on population growth.
4. CONCLUSIONS AND DISCUSSION
Davidia involucrata has complex life-history processes represented mainly in its reproduction, that is, it can produce offspring through either seeds or vegetative buds. In the observed population, the numbers of sexually reproductive individuals (53.69%) and coppice shoots (46.31%) were similar. However, the population composed of both sexually reproductive individuals and coppice shoots showed a tendency to increase, but the sexually reproductive population without coppice shoots was declining rapidly. The sensitivity analysis showed that vegetative propagation had greater impact on population growth than did the seed reproduction, and asexual reproduction had the most important contribution to the population dynamics than sexually reproduction. Therefore, the existence of coppice shoots kept the numbers of individuals in the population high enough to increase the probability of the population surviving.
The sensitivity analysis showed that the population growth rate was influenced more readily by individual growth, which had contributions of more than 59%. For population growth, seed germination rate had the largest impact, and seedling survival rate had the next-largest impact. In nature, however, both of these vital rates were so low that the accumulation of seedlings in the population was more difficult, the numbers of sexually reproductive individuals were limited and even the distribution of individuals over different life stages was not ideal or even stable. Thus, the fates of seeds and seedlings were the most important factors leading the population to decline, and the result is similar to that reported by Su et al. [51]. Raising the seed germination rate and the survival rate of seedlings is an effective way to conserve the forest population.
Different life-history stages had different impacts on population growth. For the overall population (including both sexual and asexual reproduction), stage III contributed the most to population growth (26.31%), with about 53.85% of the contribution provided by clonal growth of the individuals in the stage. When asexual reproduction was ignored, the seed stage became the most important stage for population growth and the stage V was the second most important stage. Also, the demographic rates with the greatest contributions were the seed germination rate for growth and the seed production rate in stage V for sexual reproduction. The seed germination rate is influenced by the quality and quantity of seeds, which are associated with mother individuals (e.g. individuals of stage V). Therefore, stage V had the most important effect on population growth, and the seed stage was the next most important stage for population growth. Ecological theory related to life-history strategies [38,59,60] suggests that adult stages of survival are most “important” for persistence of long-lived species. Our study for Davidia involucrata population supports this theory, as the late adult stage (stage V) is the most important.
More notable is that human disturbance is an important factor causing the variation and even degradation of the Davidia involucrata population. In our study area, the Davidia involucrata community had been damaged many times by human activities such as felling trees, picking seeds and digging up seedlings, which increased the coppice shoots, decreased the numbers of seeds and seedling, and destroyed the habitat.
Our results demonstrate that the current population of Davidia involucrata faced a potential crisis of decline or even extinction due to its reliance on asexual reproduction. For conservation of actual populations, improvements in sexual reproduction will increase population growth rate more than will similar improvements in asexual reproduction. Similarly, proportional improvements in both stage V and the seed stage increase population growth more than like improvements in stage III survival.
5. ACKNOWLEDGEMENTS
We wish to thank Prof. Dr. Elgene O. Box (University of Georgia) for editing the English. This study was supported by the national scientific and technological program of SFA (No. 2008BADB0B04).
REFERENCES
- Li, B., Yuan, D.-L., Ban, J.-D., Song, J.-Z., Gou, D.-G., Wang, B.-Q. and Su, C.-J. (1990) Dovetree community of Mt. Seven-sister in western Hubei & its protective strategies. Journal of Central China Normal University (Natural Science), 21, 323-334.
- Wu, G., Han, S.-H., Wang, H.-C., Luo, Y.-C., Deng, H.-B. and Zhao, J.-Z. (2004) Living characteristics of rare and endangered species—Davidia involucrata. Journal of Forestry Research, 15, 39-44. doi:10.1007/BF02858008
- Zhang, Q.-H. (1992) Investigation of Dove tree’s natural distribution. In: The Propagation Technology of Rare and Endangered Tree Species Editorial Committee, Ed., The Propagation Technology of Rare and Endangered Tree Species, China Forestry Publishing House, Beijing, 25- 30.
- Tao, J.-C., Zong, S.-X. and Yang Z.-B. (1986) The geographical distribution and introduction of Davidia involucrata. Journal of Zhejiang Forestry College, 3, 25- 33.
- Yang, Y.-C. and Li, T.-J. (1989) Preliminary studies on the phytocommunity of Davidia involucrata in Omei Mountain of Sichuan. Acta Phytoecologica et Geobotanica Sinica, 13, 270-276.
- Zhang, J.-X., Li, J.-Q. and Zhou, B.-S. (1995) Natural distribution of Davidia involucrata and introduction analysis. Journal of Beijing Forestry University, 17, 25-30.
- Hu, J.-Y., Su, Z.-X. and Li, Y.-X. (2003) Research advance on Dove tree biology. Chinese Wild Plant Resources, 22, 15-19.
- Wu, J.-G. and Lu, J.-J. (2009) Potential effects of climate change on the distribution of Dove trees (Davidia involucrata Baill.) in China. Research of Environmental Sciences, 22, 1371-1381.
- Zhang, J.-X., Li, J.-Q. and Lian, X.-R. (1994) Morphology and biological characteristics of Davidia involucrata. Journal of Beijing Forestry University, 16, 33-37.
- Fan, C. and Li, X.-W. (2004) Progress in Davidia involucrata research. Forestry Science & Technology, 29, 55- 58.
- Si, J.-Y., Lei, N.-Y., Si, P.-Y. and Li, J.-Q. (2009) Review of studies on Davidia involucrata Baill. Science Technology and Engineering, 19, 3713-3719.
- Li, Y.-M. (2003) Population viability analysis in conservation biology: Precision and uses. Biodiversity Science, 11, 340-350.
- Yu, Y.-T., Xu, G.-B. and Wang, X.-P. (2006) Literature review of researches on Davidia involucrata Baill. Nonwood Forest Research, 24, 92-94.
- Ai, X.-R. and Tan, J.-X. (1999) On the population structure of in Xingdoushan protected region. Journal of Hubei Institute for Nationalities, 17, 12-15.
- Dang, H.-S., Jiang, M.-X., Tian, Y.-Q., Huang, H.-D. and Jin, X. (2004) Population structure and distribution pattern of rare plant communities in Houhe nature reserve. Chinese Journal of Applied Ecology, 15, 2206-2210.
- Ma, Y.-F. and Li, J.-Q. (2005) Population structure of Davidia involucrata in Mt. Seven-sister nature reserve of central China’s Hubei province. Journal of Beijing Forestry University, 27, 12-16.
- Zhang, Y.-S., Su, Z.-X. and Hu, J.-Y. (2005) Spatial distribution pattern of Davidia involucrata population. Acta Botanica Yunnanica, 27, 395-402.
- Zhang, W., Cao, G.-X., Liu, G.-H. and Liu, X. (2008) Population structure and distribution pattern of Davidia involucrata at Labahe nature reserve of Sichuan province. Journal of Zhejiang Forestry College, 25, 451-457.
- Luo, S.-J., Bao, M.-Z., Zhao, S.-X., Xie, Z.-G. and Yang, Y.-J. (2009) Spatial distribution pattern of Davidia involucrata population in Longcanggou in Daxiangling nature reserve. Journal of Biomathematics, 24, 531-536.
- Jiao, J. (1999) Studies on the interspecific association of Davidia involucrata community’s dominant species in Wen county of Gansu. Journal of Gansu Agricultural University, 34, 61-64.
- Hu, L.-L., Li, X., Jiang, M.-X., Huang, H.-D., Man, J.-S. and Su, C.-J. (2003) Studies on the interspecific association of canopy trees in community of Mt. Seven-sister in western Hubei. Journal of Wuhan Botanical Research, 21, 203-208.
- Zhu, L.-J., Su, Z.-X., Wang, W.-W. and Zhang, Y.-S. (2005) Numerical analysis on interspecific relationships in Davidia involucrata community in Sanjiang Wolong nature reserve. Chinese Journal of Ecology, 24, 1167-1171.
- Zhu, L.-J., Su, Z.-X., Hu, J.-Y., Su, R.-J. and Zhou, L. (2006) Studies on the relationship of species in Davidia involucrata community. Guibaia, 26, 32-37.
- Li, Y., Su, Z.-X., Zhang, S.-L., Hu, J.-Y. and Zhu, L.-J. (2006) Intraspecific and interspecific competition in Davidia involucrata (Davidiaceae) community. Acta Botanica Yunnanica, 28, 625-630.
- Jiao, J., Tian, B.-S. and Sun, X.-G. (1998) Population patterns and dynamics of community’s dominant species in Wen county of Gansu. Journal of Gansu Agricultural University, 33, 266-271.
- Lei, N.-Y., Chen, Y., Li, J.-Q. and Tang, X.-J. (2007) Regeneration and stability of Davidia involucrata population in Xiaoliangshan Mountain, Sichuan province. Journal of Beijing Forestry University, 29, 26-30.
- Cheng, Y. (2008) Study on biodiversity and natural regeneration of Davidia involucrata community in Wuling Mountain. Forest Inventory and Planning, 33, 1-4.
- He, J.-S., Lin, J. and Chen, W.-L. (1995) The current status of endemic and endangered species Davidia involucrata and the preserving strategies. Chinese Biodiversity, 3, 213-221.
- Zhang, Z.-Y., Su, Z.-X. and Shen, A.-Y. (2003) The biological character, endangered causes and protection of Davidia involucrata Baill, an endemic to China. Journal of Huaiyin Teachers College (Natural Science Edition), 2, 66-69.
- Menges, E.S. (1986) Predicting the future of rare plant populations: Demographic monitoring and modeling. Natural Areas Journal, 6, 13-25.
- Menges, E.S. (1990) Population viability analysis for an endangered plant. Conservation Biology, 4, 52-62. doi:10.1111/j.1523-1739.1990.tb00267.x
- Crouse, D.T., Crowder, L.B. and Caswell, H. (1987) A stage-based population model for loggerhead sea turtles and implications for conservation. Ecology, 68, 1412- 1423. doi:10.2307/1939225
- Lande, R. (1988) Demographic models of the northern spotted owl (Strix occidentalis caurina). Oecologia, 75, 1082-1093. doi:10.1007/BF00776426
- Boyce, M.S. (1992) Population viability analysis. Annual Review of Ecology and Systematics, 23, 481-506. doi:10.1146/annurev.es.23.110192.002405
- Horvitz, C.C. and Schemske, D.W. (1995) Spatiotemporal variation in demographic transitions of a tropical understory herb: Projection matrix analysis. Ecological Monographs, 65, 155-192. doi:10.2307/2937136
- Leslie, P.H. (1945) On the use of matrices in certain population mathematics. Biometrika, 33, 183-212. doi:10.1093/biomet/33.3.183
- Leslie, P.H. (1948) Some further notes on the use of matrices in population mathematics. Biometrika, 35, 213- 245.
- Wisdom, M.J., Mills, L.S. and Edoak, D. (2000) Life stage simulation analysis: Estimating vital-rate effects on population growth for conservation. Ecology, 8, 628-641.
- Lefkovitch, L.P. (1965) The study of population growth in organisms grouped by stages. Biometrics, 21, 1-18. doi:10.2307/2528348
- Hartshorn, G.S. (1975) A matrix model of tree population dynamics. In: Golley, F.B. and Medina, E., Eds., Tropical Ecological Systems, Springer-Verlag, New York, 41-51. doi:10.1007/978-3-642-88533-4_4
- Werner, P.A. and Caswell, H. (1977) Population growth rates and age versus stage-distribution models for teasel (Dipsacus sylvestris Huds.). Ecology, 58, 1103-1111. doi:10.2307/1936930
- Cochran, M.E. and Ellner, S. (1992) Simple methods for calculating age-based life history parameters for stagestructured populations. Ecological Monographs, 62, 345- 364. doi:10.2307/2937115
- Caswell, H. (1997) Matrix methods for population analysis. In: Tuljapurar, S. and Caswell, H., Eds., StructuredPopulation Models in Marine, Terrestrial, and Freshwater Systems, Chapman and Hall, New York, 19-58. doi:10.1007/978-1-4615-5973-3_2
- de Kroon, H., Plaisier, A., van Groenendael, J. and Caswell, H. (1986) Elasticity: The relative contribution of demographic parameters to population growth rate. Ecology, 67, 1427-1431. doi:10.2307/1938700
- van Groenendael, J., de Kroon, H. and Caswell, H. (1988) Projection matrices in population biology. Trends in Ecology and Evolution, 3, 264-269. doi:10.1016/0169-5347(88)90060-2
- Schemske, D.W., Husband, B.C., Ruckelshaus, M.H., Goodwillie, C., Parker, I.M. and Biship, J.G. (1994) Evaluating approaches to the conservation of rare and endangered plants. Ecology, 75, 584-606. doi:10.2307/1941718
- Horvitz, C.C., Schemske, D.W. and Caswell, H. (1997) The relative “importance” of life history stages to population growth: Prospective and retrospective approaches. In: Tuljapurkar, S. and Caswell, H., Eds., Structured Population Models in Marine, Terrestrial, and Freshwater System, Chapman and Hall, New York, 247-272. doi:10.1007/978-1-4615-5973-3_7
- de Kroon, H., van Groenendael, J. and Ehrlén, J. (2000) Elasticities: A review of methods and model limitations. Ecology, 81, 607-618. doi:10.1890/0012-9658(2000)081[0607:EAROMA]2.0.CO;2
- Chen, K.-R., Li, T.-S., Tian, G.-H., Zhao, D.-Q. and He, L.-G. (1998) The biological characteristics in Dove tree Davidia involucrata propagation. Journal of Southwest Forestry College, 18, 68-73.
- Li, Y.-X. (2003) Present state and perspectives of biological study on Davidia involucrata. Journal of China West Normal University (Natural Sciences), 24, 269-275.
- Su, R.-J. and Su, Z.-X. (2005) Study on relations of seed dispersal, germination and age-class distribution in population in Davidia involucrata. Scientia Silvae Sinicae, 41, 192-195.
- Qu, Z.-X. (1952) Analysis on forest actuality in Linggu Temple of Nanjing. Acta Botanica Sinica, 1, 18-49.
- Liu, J.-F. and Hong, W. (1999) A study on forecast of population dynamics of Castanopsis kawakamii. Chinese Journal of Applied Environment Biology, 5, 247-253.
- Sebert-Cuvillier, E., Paccaut, F., Chabrerie, O., Endels, P., Goubet, O. and Decocq, G. (2007) Local population dynamics of an invasive tree species with a complex lifehistory cycle: A stochastic matrix model. Ecological Modelling, 201, 127-143. doi:10.1016/j.ecolmodel.2006.09.005
- Zheng, Y.-R., Zhang, X.-S. and Xu, W.-D. (1997) Model forecast of population dynamics of spruce on sandy land. Acta Phytoecologica Sinica, 21, 130-137.
- Lamberson, R.H., Noon, C. and McKelvey, K. (1994) Reserve design for terrestrial species: The effects of patch size and spacing on the viability of the Northern Spotted Owl. Conservation Biology, 8, 185-195. doi:10.1046/j.1523-1739.1994.08010185.x
- Silvertown, J., Franco, M., Pisanty, I. and Mendoza, A. (1993) Comparative plant demography relative importance of life-cycle components to the finite rate of increase in woody and herbaceous perennials. Journal of Ecology, 81, 465-476. doi:10.2307/2261525
- Caswell, H. and Trevisan, M.C. (1994) The sensitivity analysis of periodic matrix models. Ecology, 75, 1299- 1303. doi:10.2307/1937455
- Pianka, E.R. (1970) On r and k selection. American Naturalist, 104, 592-597. doi:10.1086/282697
- Southwood, T.R.E., May, R.M., Hassell, M.P. and Conway, G.R. (1974) Ecological strategies and population parameters. American Naturalist, 108, 791-804. doi:10.1086/282955

