Natural Science
Vol.4 No.1(2012), Article ID:16593,6 pages DOI:10.4236/ns.2012.41011
Modified atomic orbital theory applied to the calculation of high-lying  Rydberg series of He-like ions
Rydberg series of He-like ions
![]()
UFR Sciences and Technologies, Department of Physics, University of Ziguinchor, Ziguinchor, Senegal; aminafatima_sakho@yahoo.fr
Received 9 September 2011; revised 14 October 2011; accepted 28 October 2011
Keywords: Atomic Orbital Theory; Screening Constant; Semi-Empirical Calculations; Autoionizing States; Rydberg Series; Helium-Like Ions
ABSTRACT
The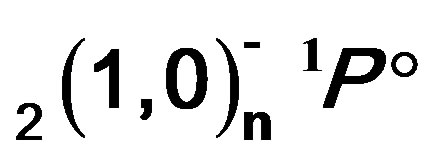 ,
, 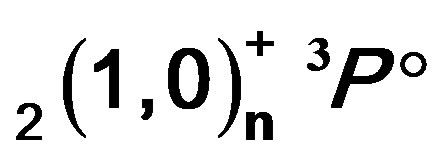 ,
, 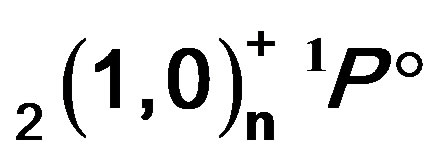 , and
, and 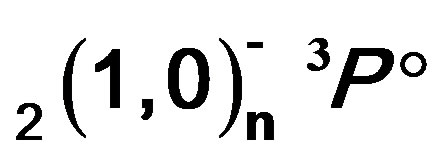 intershell Rydberg series of the he- lium-like ions are investigated in the framework of the modified Atomic Orbital Theory (MAOT). Highlying energy resonances of He and excitation energy of the helium-like Li+ up to n = 10 are tabulated. In addition, total energy positions for lowlying states (n £ 4) of the helium-isoelectronic sequence with Z = 2, 3,
intershell Rydberg series of the he- lium-like ions are investigated in the framework of the modified Atomic Orbital Theory (MAOT). Highlying energy resonances of He and excitation energy of the helium-like Li+ up to n = 10 are tabulated. In addition, total energy positions for lowlying states (n £ 4) of the helium-isoelectronic sequence with Z = 2, 3,  10 are also presented. All the current results agreed well with the published values. The data listed in this paper may be useful guideline for future experimental and theoretical studies in high-lying 1,3P˚ autoionizing states of two-electron systems.
10 are also presented. All the current results agreed well with the published values. The data listed in this paper may be useful guideline for future experimental and theoretical studies in high-lying 1,3P˚ autoionizing states of two-electron systems.
1. INTRODUCTION
Studies of excited states in two electron systems have been an active field of research both experimentally and theoretically since the earlier synchrotron radiation source experiment of Madden and Codling on He [1]. At present, the description of the properties of the excited states in the helium isoelectronic series is done in the framework of the new classification scheme with the label 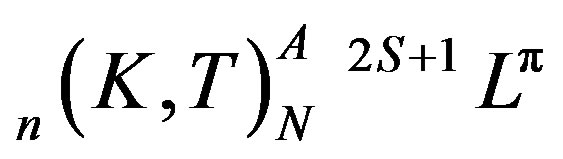 . In this notation, N and n denote respectively the principal quantum numbers of the inner and of the outer electron, S the total spin, L the total angular momentum, p the parity of the system, K and T are angular correlation quantum numbers and A represents the radial correlation quantum number of the two electrons. Besides, this designation incorporates singly excited states and both intrashell and intershell excited states in the helium-like ions. A given channel µ is labelled by
. In this notation, N and n denote respectively the principal quantum numbers of the inner and of the outer electron, S the total spin, L the total angular momentum, p the parity of the system, K and T are angular correlation quantum numbers and A represents the radial correlation quantum number of the two electrons. Besides, this designation incorporates singly excited states and both intrashell and intershell excited states in the helium-like ions. A given channel µ is labelled by 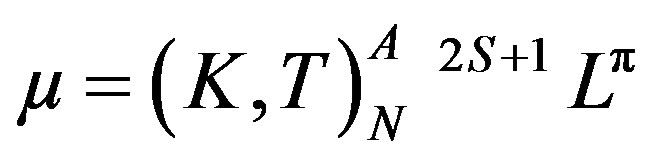 as originally used by Herrick and Sinanoglu [2,3] with the following assignment of K and T for a given N, L and p T = 0, 1, 2,
as originally used by Herrick and Sinanoglu [2,3] with the following assignment of K and T for a given N, L and p T = 0, 1, 2, , min(L, N – 1).
, min(L, N – 1).
K = N – 1 – T, N – 3 – T, , – (N – 1 – T).
, – (N – 1 – T).
These assigned values of K and T depend not on the total angular spin S. Besides, T is roughly speaking the projection of L onto the interelectronic axis and describes then the orientations between the orbitals of the two electrons and K is related to cosinus of the interelectronic angle as K » – ár< cosq12ñ where r< denotes the radius of the inner electron. Physically, the larger the positive value of K, the value of 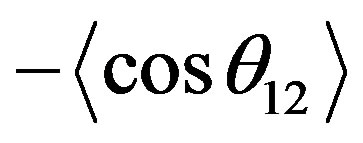 is closer to unity. In addition, A can take the values +1 or – 1 and 0 only [4,5]. For the A = +1 states, the two electrons tend to approach or to move away from the nucleus in phase and for A = –1 states, the two electrons have out-of-phase such that, when one electron approaches the nucleus, the other tends to move away from it [4,5]. For A = 0 states, they are little radial correlation between the two electrons and they are similar to singly excited states [4,5].
is closer to unity. In addition, A can take the values +1 or – 1 and 0 only [4,5]. For the A = +1 states, the two electrons tend to approach or to move away from the nucleus in phase and for A = –1 states, the two electrons have out-of-phase such that, when one electron approaches the nucleus, the other tends to move away from it [4,5]. For A = 0 states, they are little radial correlation between the two electrons and they are similar to singly excited states [4,5].
In the description of the autoionizing states in two electron systems, various methods are used. Among these methods are the saddle-point complex-rotation method [6], the close-coupling method [7], the truncated-diagonalization method [8], the complex-coordinate rotation [9-11], the computing double sum over the complete hydrogen spectrum [12], the screening constant by unit nuclear charge formalism [13-15], the Debye screening model [16]. Except for the screening constant by unit nuclear charge method based on a semi-empirical formalism, most of the preceding methods present special theoretical and computational problems. To overcome these problems, we apply in this paper the modified atomic orbital theory (MAOT) we present recently [17,18]. The MAOT formalism is then used to study the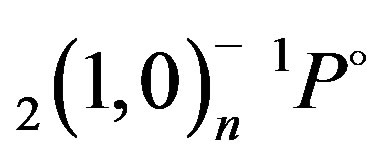 ,
, 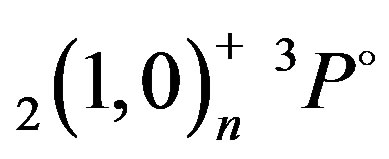 ,
, 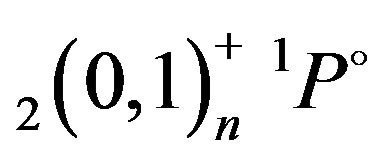 , and
, and
 intershell Rydberg series of the helium-like ions up to Z = 10 and n = 10.
intershell Rydberg series of the helium-like ions up to Z = 10 and n = 10.
Then, in this paper, energies for high-lying 1,3P˚ autoionizing states of He-like ions below the N = 2 hydrogenic thresholds are tabulated using the modified atomic orbital theory (MAOT) in the framework of a semi-empirical procedure. The results up to Z = 10 compare well to some theoretical results. In addition, it is also demonstrated in the present work, the adequacy of the MAOT’s formalism to separately identify the classification (+, -) of the 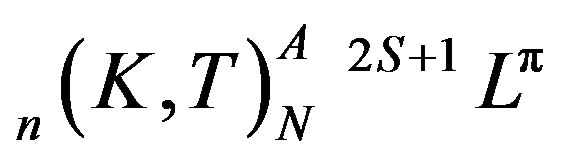 Rydberg states without complex calculations. The data quoted in this work may be of interest for future experimental and theoretical investigations in high-lying 1,3P˚ Rydbergs series of two-electron systems.
Rydberg states without complex calculations. The data quoted in this work may be of interest for future experimental and theoretical investigations in high-lying 1,3P˚ Rydbergs series of two-electron systems.
In Section 2, we present the theoretical procedure adopted in this work.
In Section 3, we present and discuss the results obtained, compared with available theoretical and experimental data.
2. THEORY
2.1. General Formalism of the MAOT Method for Excited States of Two Electron Systems
In the framework of Modified Atomic Orbital Theory (MAOT), total energy of a (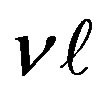 )-given orbital is expressed in the form [17,18]
)-given orbital is expressed in the form [17,18]
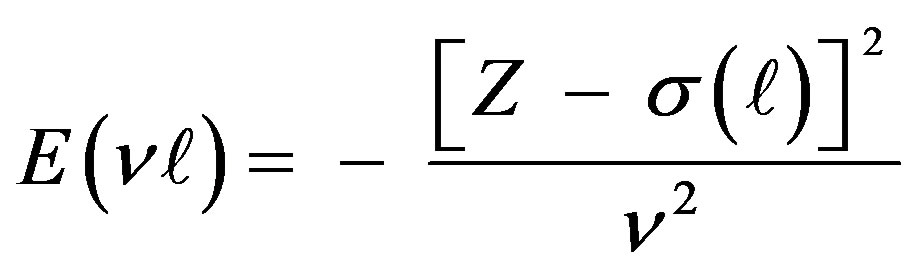 . (1)
. (1)
For an atomic system of several electrons M, the total energy is given by (in rydbergs):
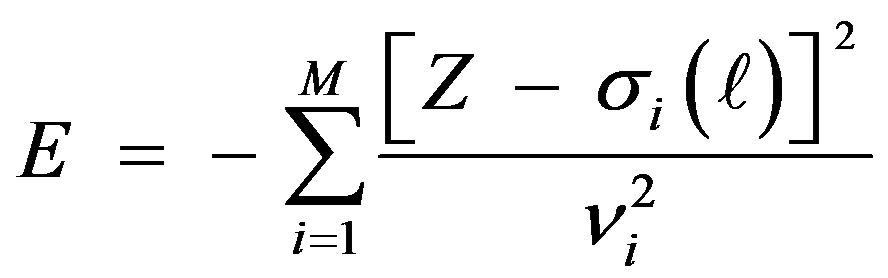 .
.
With respect to the usual spectroscopic notation  , this equation becomes
, this equation becomes
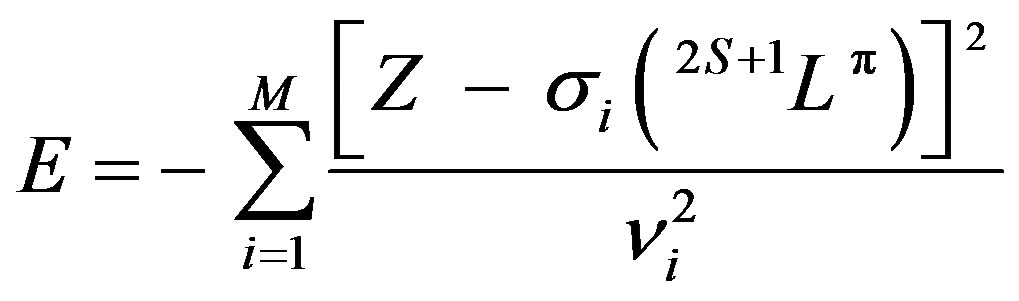 . (2)
. (2)
With regard to the new classification scheme, Eq.2 takes the form
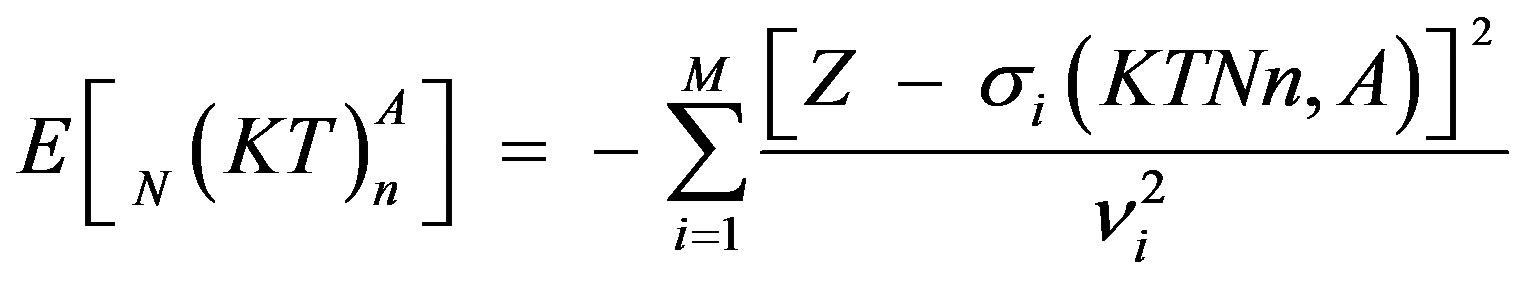
For two electron systems which are the intention of the present work, we obtain
 (3)
(3)
2.2. Energies for 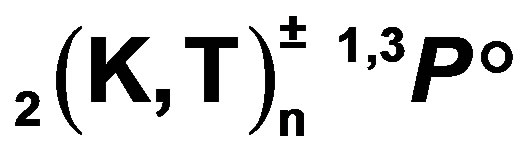 Doubly Excited States of He Isoelectronic Sequence
Doubly Excited States of He Isoelectronic Sequence
Total energies for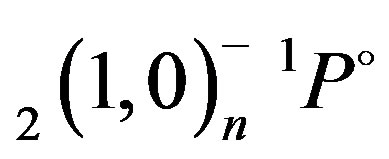 ,
, 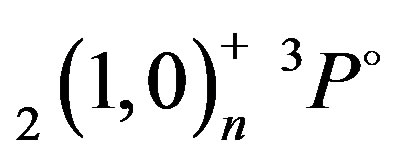 ,
, 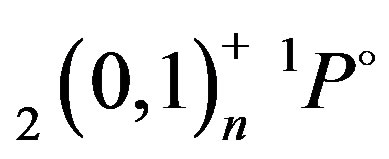 , and
, and  autoionizing states of two-electron systems are respectively given by
autoionizing states of two-electron systems are respectively given by
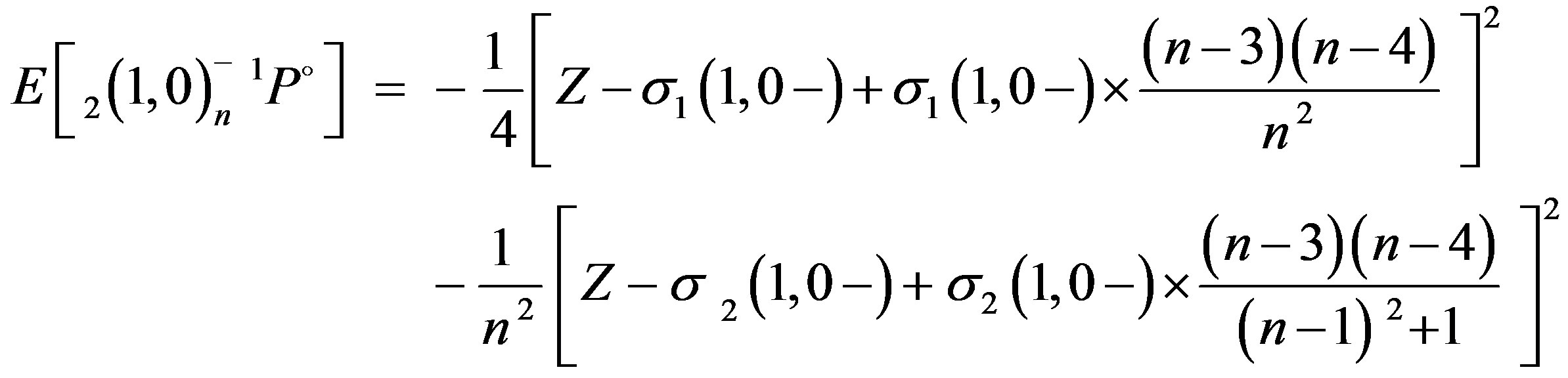 (4.a)
(4.a)
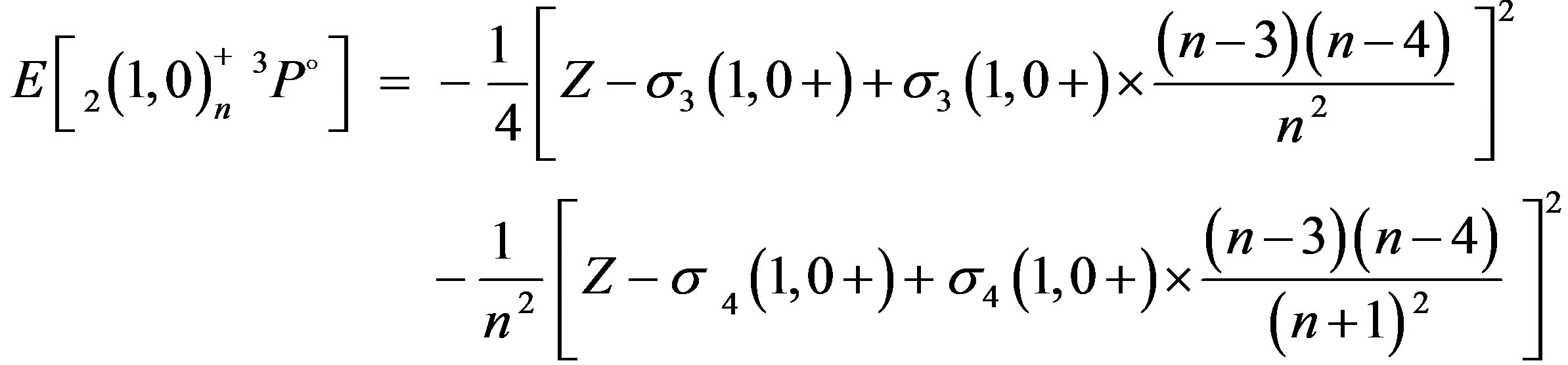 (4.b)
(4.b)
 (4.c)
(4.c)
 (4.d)
(4.d)
For the empirical evaluation of the si-screening constants in Eq.4, we use the experimental energy results of electron ejected of Hicks and Comer [19] and photoabsorption experiments of Madden and Codling [1] on He along with photoionisation experimental values of Diehl et al. [20] of Li+ quoted in Table 1. These energies are measured with respect to the ground state of the corresponding system. On the basis of these experimental data, the si-semi-empirical screening constants are evaluated using Eq.4. The results obtained are listed in the last column of Table 1.
3. RESULTS AND DISCUSSIONS
The results of the present calculations for the energy resonances of 1,3P˚ states below the N = 2 hydrogenic thresholds are listed in Tables 2-4. In Table 2, we present a comparison of energy resonance of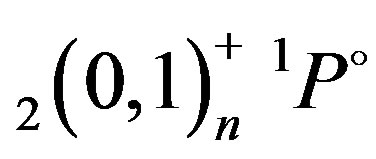 ,
, 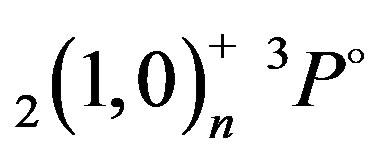 ,
, 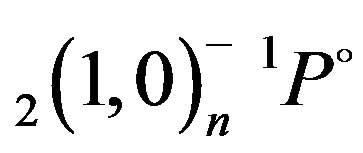 and
and 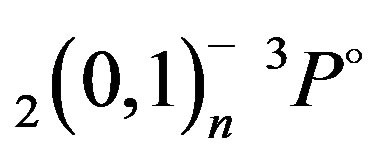 autoionizing states of the helium atom obtained from the present
autoionizing states of the helium atom obtained from the present
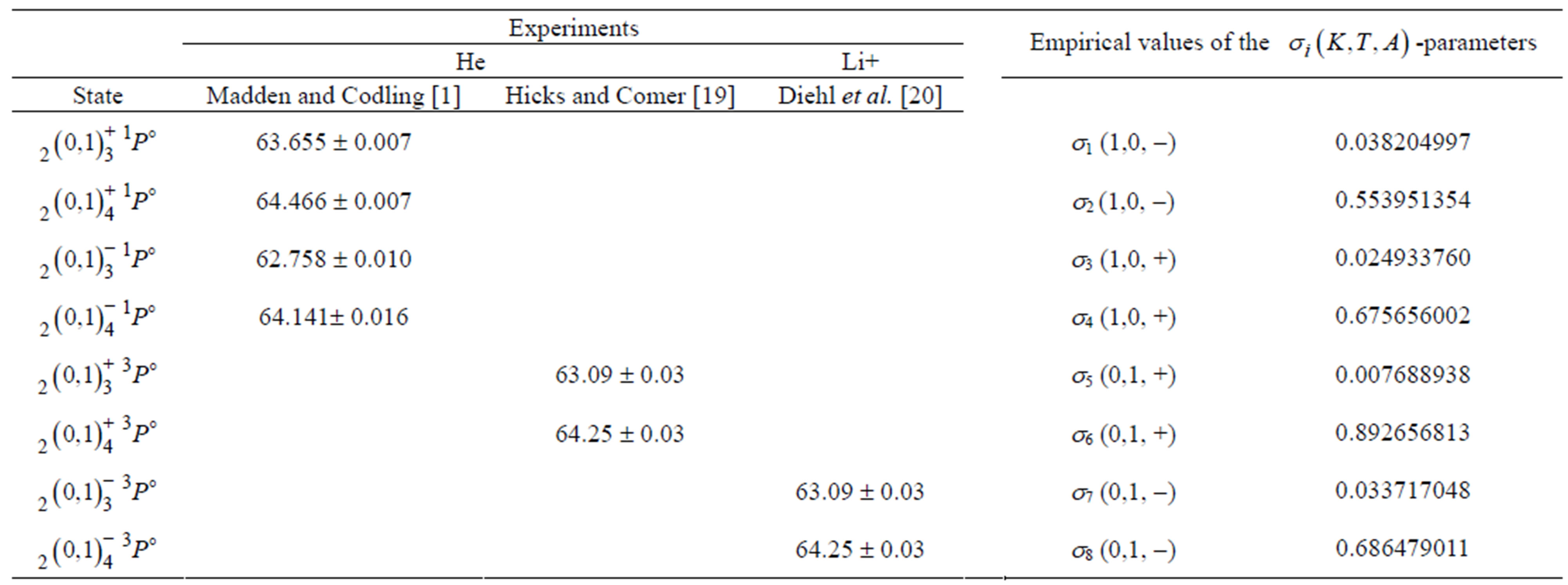
Table 1. Experimental energy resonances (E) of 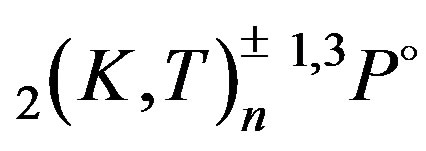 doubly excited states of He and Li+ used to evaluate empirically the si-screening constants in Eq.4. The empirical data of the si-parameters are quoted in last column of the table. The energy values are reported in eV. For energy conversion, the ground state energy of He at −79.01 eV and that of Li+ equals to −198.09 eV are used along with the infinite rydberg: 1Ry = 13.605698 eV.
doubly excited states of He and Li+ used to evaluate empirically the si-screening constants in Eq.4. The empirical data of the si-parameters are quoted in last column of the table. The energy values are reported in eV. For energy conversion, the ground state energy of He at −79.01 eV and that of Li+ equals to −198.09 eV are used along with the infinite rydberg: 1Ry = 13.605698 eV.
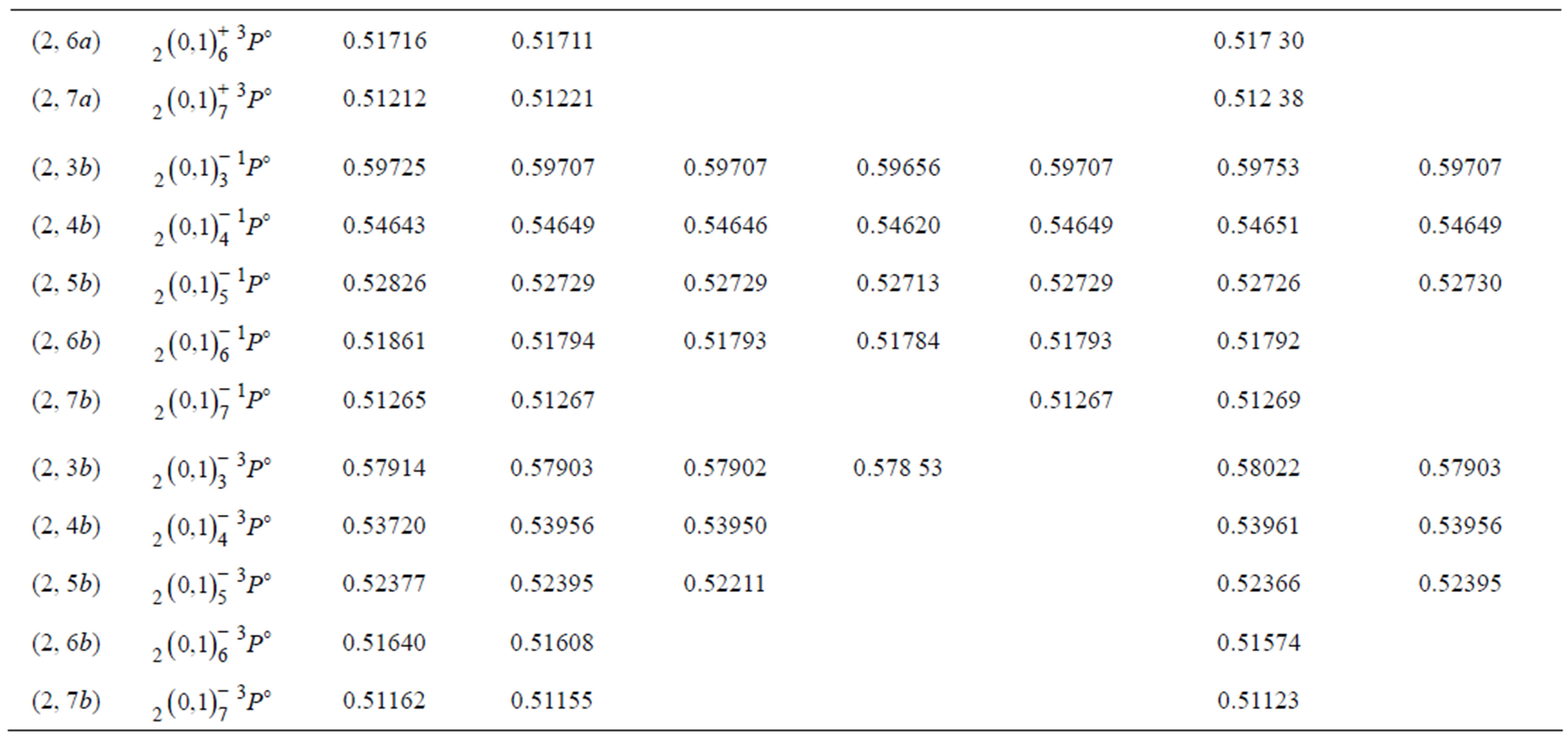
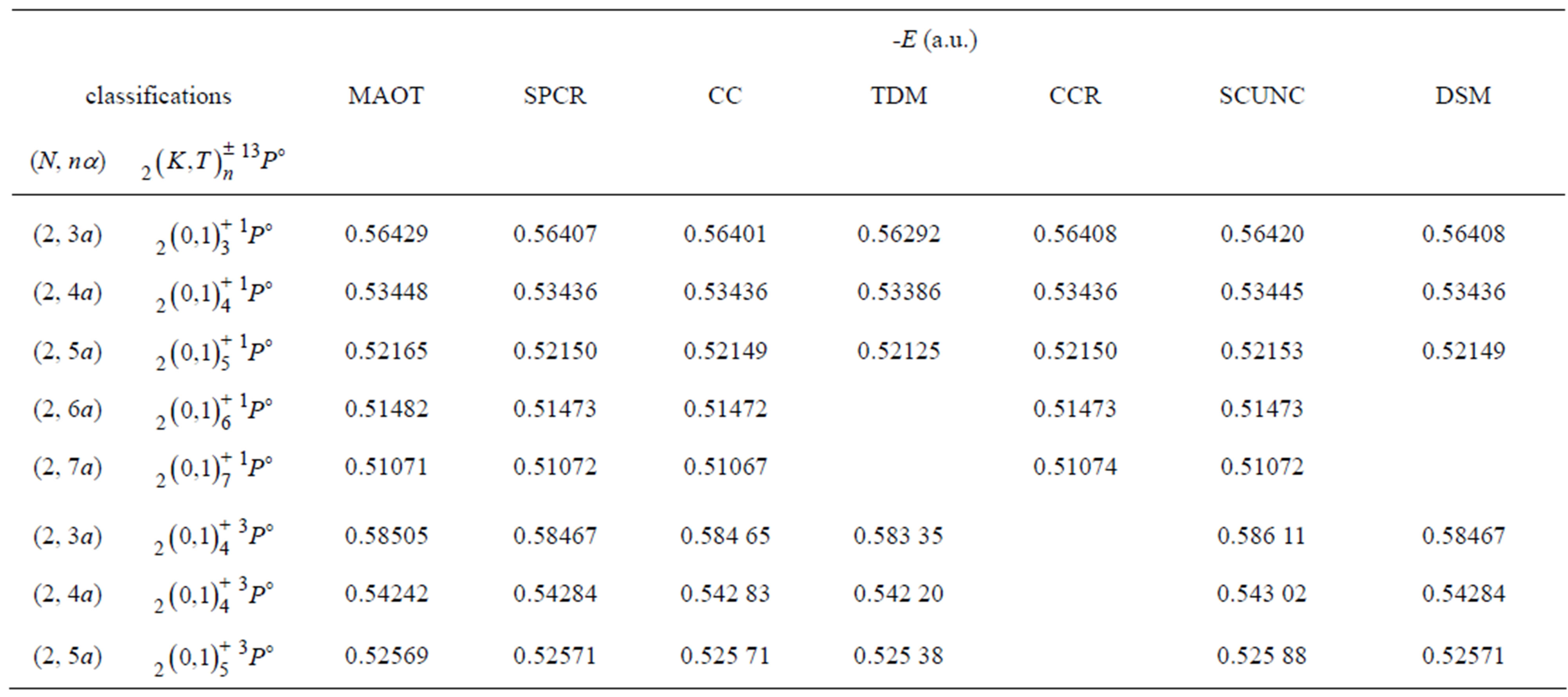
Table 2. Comparison of our results from the present modified atomic orbital theory (MAOT) with other theoretical results of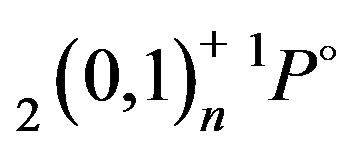 ,
, 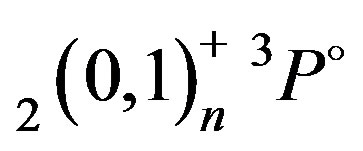 ,
,  and
and 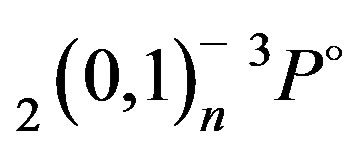 autoionizing states of the helium atom: saddle-point complex-rotation method (SPCR), Chen [6]; close-coupling method (CC), Oza [7]; truncated-diagonalization method (TDM), Conneely and Lipsky [8], complex coordinate rotation (CCR), Ho [9], Screening constant by unit nuclear charge (SCUNC) results, Sakho [15], results from Debye screening model (DSM), Kar and Ho [16].
autoionizing states of the helium atom: saddle-point complex-rotation method (SPCR), Chen [6]; close-coupling method (CC), Oza [7]; truncated-diagonalization method (TDM), Conneely and Lipsky [8], complex coordinate rotation (CCR), Ho [9], Screening constant by unit nuclear charge (SCUNC) results, Sakho [15], results from Debye screening model (DSM), Kar and Ho [16].
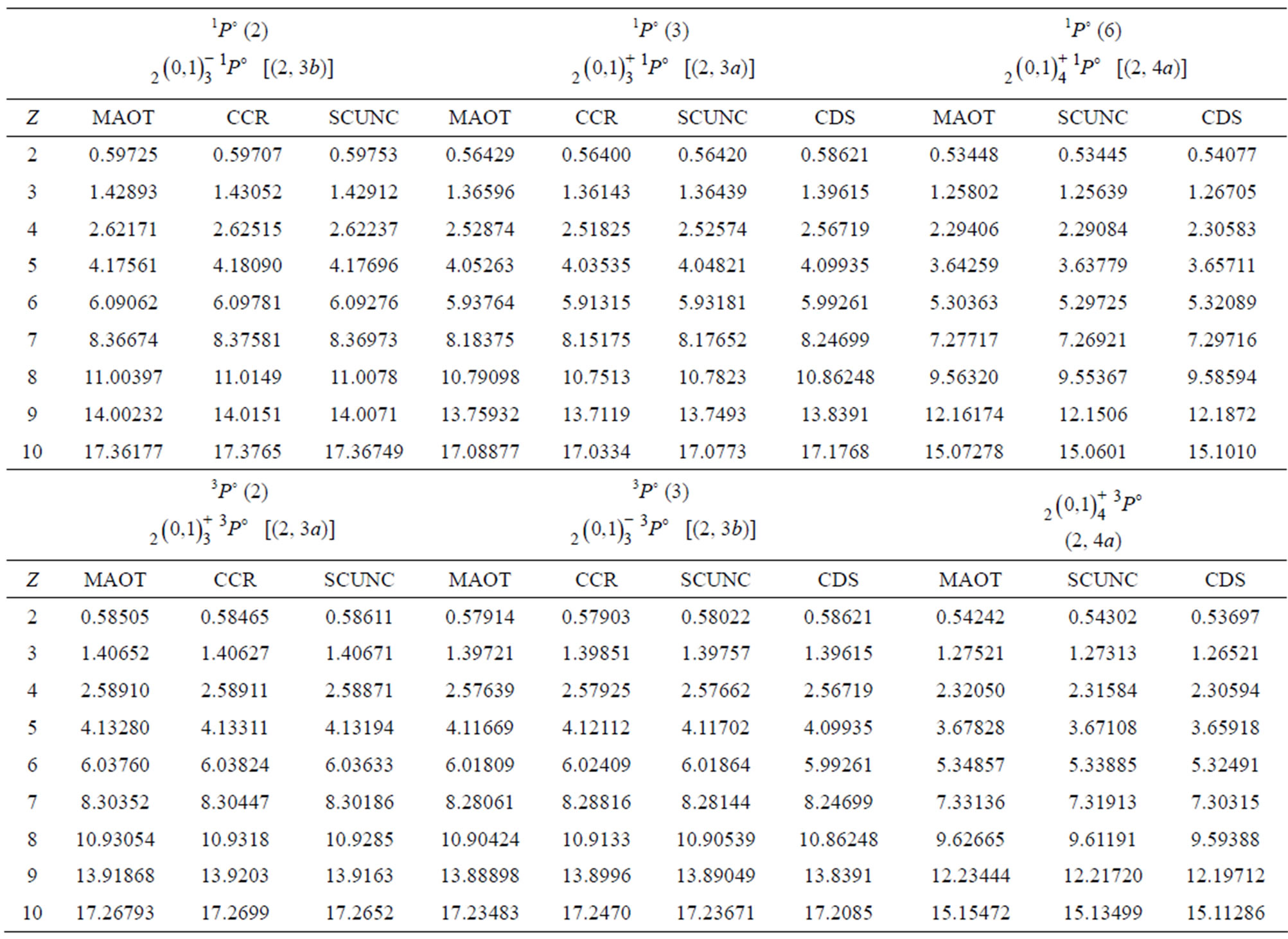
Table 3. Comparison of our results from the present modified atomic orbital theory (MAOT) for some 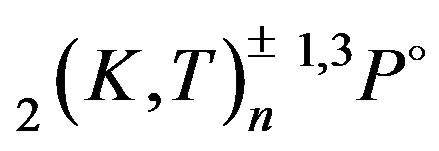 autoionizing states of the helium isoelectronic sequence with complex-coordinates rotation method (CCR), Ho [10] and computing double sum method (CDS) over the complete hydrogen spectrum Ivanov and Safronova [12]. Screening constant by unit nuclear charge (SCUNC) results [15]. All results are expressed in atomic units.
autoionizing states of the helium isoelectronic sequence with complex-coordinates rotation method (CCR), Ho [10] and computing double sum method (CDS) over the complete hydrogen spectrum Ivanov and Safronova [12]. Screening constant by unit nuclear charge (SCUNC) results [15]. All results are expressed in atomic units.
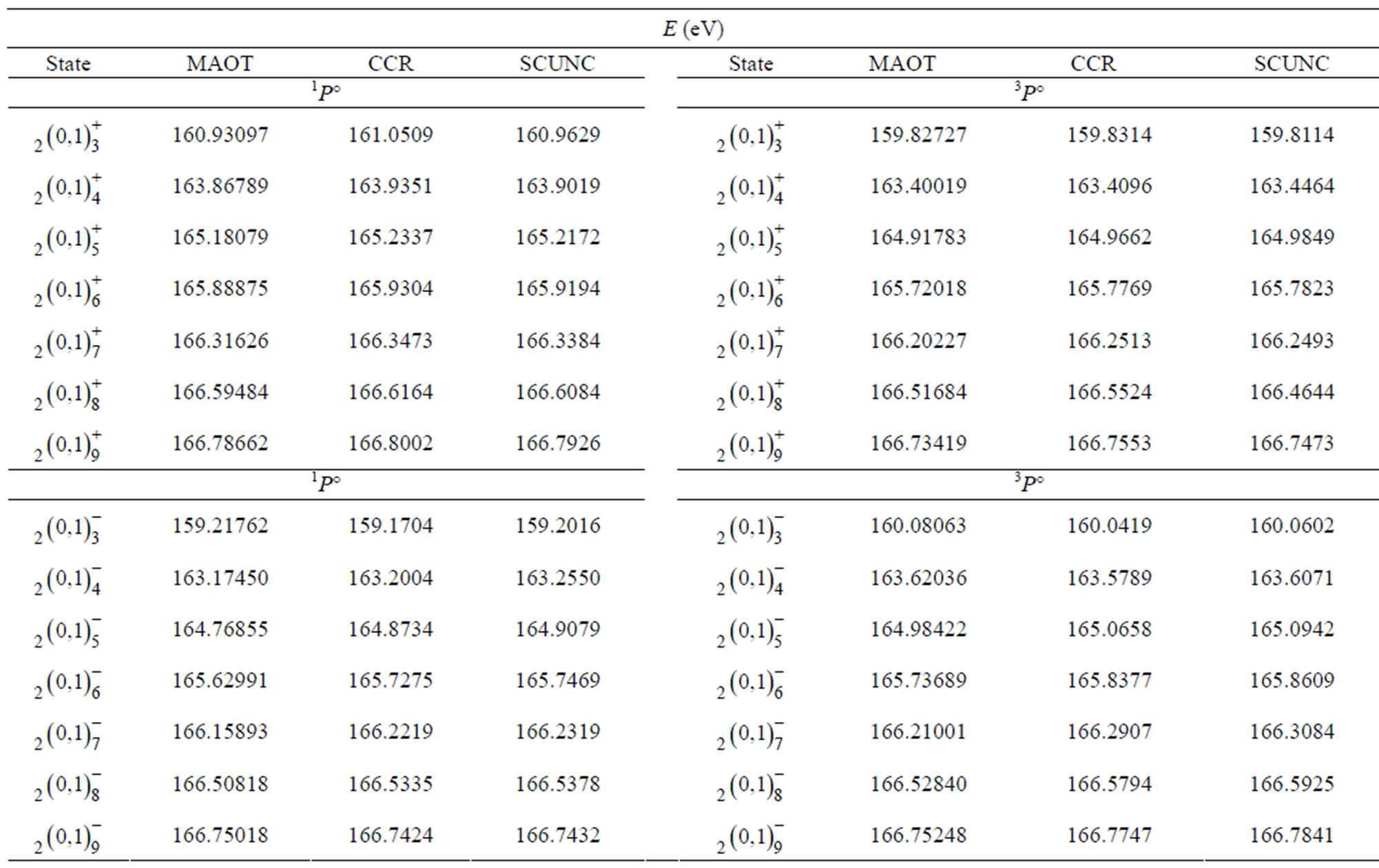
Table 4. Comparison of our results from the present modified atomic orbital theory (MAOT) for excitation energies of 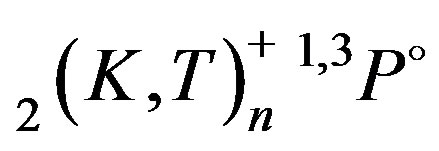 and
and 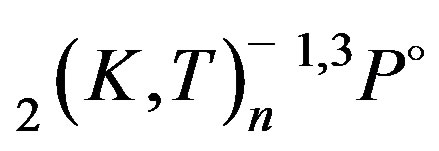 autoionizing states of Li+ complex—coordinate rotational (CCR) results Chung and Lin [11]. Here and in [11], the energy of each state is measured from the ground state of Li equals to—07.280521a.u with 1 a.u. (7Li) = 27.20927 eV, which includes the reduced mass correction. Screening constant by unit nuclear charge (SCUNC) results [15]. All results are expressed in eV.
autoionizing states of Li+ complex—coordinate rotational (CCR) results Chung and Lin [11]. Here and in [11], the energy of each state is measured from the ground state of Li equals to—07.280521a.u with 1 a.u. (7Li) = 27.20927 eV, which includes the reduced mass correction. Screening constant by unit nuclear charge (SCUNC) results [15]. All results are expressed in eV.
modified atomic orbital theory (MAOT) with the saddle-point complex-rotation method (SPCR) [8], the closecoupling method [9], the truncated-diagonalization method (TDM) [10], the complex coordinate rotation (CCR) [21], the screening constant by unit nuclear charge (SCUNC) results [15] and with the data from Debye screening model (DSM) [16]. The calculations agree well with each other. Table 3 indicates the present MAOT calculations for some 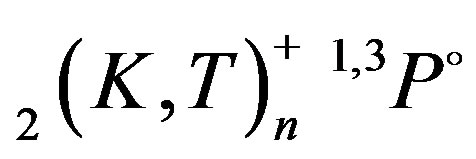 autoionizing states of the helium isoelectronic sequence (Z = 2 - 10) compared to the CCR data [13], the SCUNC results [15] and to the CDS calculations [12]. It is seen that the present results compared well to both CCR [13], SCUNC [15], and DSM [16] results. As far as the slight discrepancies between the MAOT results and that from CDS, they are mainly due to the fact that the formalism of Ivanov and Safronova [12] is done in the framework of the independent particles model which disregards the classification (+, -) of the supermultiplets investigated. This may point out the merit of the present MOAT formalism to identify separately the classification of the
autoionizing states of the helium isoelectronic sequence (Z = 2 - 10) compared to the CCR data [13], the SCUNC results [15] and to the CDS calculations [12]. It is seen that the present results compared well to both CCR [13], SCUNC [15], and DSM [16] results. As far as the slight discrepancies between the MAOT results and that from CDS, they are mainly due to the fact that the formalism of Ivanov and Safronova [12] is done in the framework of the independent particles model which disregards the classification (+, -) of the supermultiplets investigated. This may point out the merit of the present MOAT formalism to identify separately the classification of the 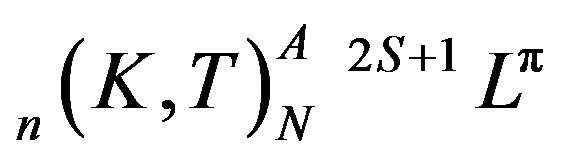 Rydberg states in the framework of a simple analytical procedure. The present calculated excitation energies of the
Rydberg states in the framework of a simple analytical procedure. The present calculated excitation energies of the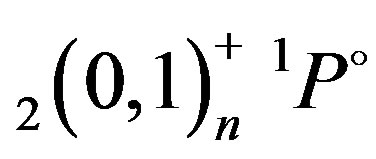 ,
, 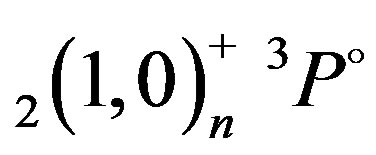 ,
, 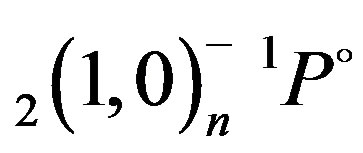 and
and 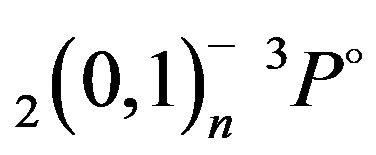 states of Li+ are listed in Table 4 and compared to the complex—coordinate rotational results of Chung and Lin [14]. These authors have included in their theory reduced mass and relativistic corrections (correction to kinetic energy, Darwin term) and stated that their calculated resonance energies are expected to be accurate within a few meV. Even if the present MAOT formalism is for non-relativistic theory and where no reduced mass corrections are included in the calculations, it can be seen a good agreement between the present results and the complex—coordinate rotational data [14]. As far as comparison with the SCUNC results is concerned, the agreement is seen to be also good. It should be mentioned that the good accuracy obtained in this paper indicates the adequacy of the MOAT formalism to treat the properties of the
states of Li+ are listed in Table 4 and compared to the complex—coordinate rotational results of Chung and Lin [14]. These authors have included in their theory reduced mass and relativistic corrections (correction to kinetic energy, Darwin term) and stated that their calculated resonance energies are expected to be accurate within a few meV. Even if the present MAOT formalism is for non-relativistic theory and where no reduced mass corrections are included in the calculations, it can be seen a good agreement between the present results and the complex—coordinate rotational data [14]. As far as comparison with the SCUNC results is concerned, the agreement is seen to be also good. It should be mentioned that the good accuracy obtained in this paper indicates the adequacy of the MOAT formalism to treat the properties of the  autoionizing states of two electron systems. The good results presented in this work may be explain by the fact that the s-fitting screening constants evaluated using experimental data incorporate implicitly relativistic corrections to the energy levels of the states investigated. In other words, the semi-empirical Formula (4) are not purely classical expressions. But, for sake of very good accuracy in the calculations, relativistic corrections and mass polarisation must be taken explicitly into account.
autoionizing states of two electron systems. The good results presented in this work may be explain by the fact that the s-fitting screening constants evaluated using experimental data incorporate implicitly relativistic corrections to the energy levels of the states investigated. In other words, the semi-empirical Formula (4) are not purely classical expressions. But, for sake of very good accuracy in the calculations, relativistic corrections and mass polarisation must be taken explicitly into account.
REFERENCES
- Madden, R.P. and Codling, K. (1963) New autoionizing atomic energy levels in He, Ne, and Ar, Physical Review Letters, 10, 516-518. doi:10.1103/PhysRevLett.10.516
- Herrick, D.R. and Sinanoglu, O. (1975) Comparison of doubly-excited helium energy levels, isoelectronic series, autoionization lifetimes, and group-theoretical configuretion-mixing predictions with large-configuration-interaction calculations and experimental spectra. Physical Review A, 11, 97-110. doi:10.1103/PhysRevA.11.97
- Sinanoglu, O. and Herrick, D.R. (1975) Group theoretic prediction of configuration mixing effects due to Coulomb repulsions in atoms with applications to doubly—Excited spectra. Journal of Chemical Physics, 62, 886-892. doi:10.1063/1.430540
- Lin, C.D. (1986), Doubly excited states, including new classification schemes. Advances in Atomic and Molecular Physics, 22, 77-142. doi:10.1016/S0065-2199(08)60335-8
- Watanabe, S. and Lin, C.D. (1986) Demonstration of moleculelike modes of doubly excited states in hyperspherical coordinates. Physical Review A, 34, 823-837. doi:10.1103/PhysRevA.34.823
- Chen M.-Keh. (1997) Doubly excited 1,3Se, 1,3Po, and 1,3De resonances in He below the n =2 He+ threshold. Physical Review A, 56, 4537-4544. doi:10.1103/PhysRevA.56.4537
- Oza, D.H. (1986) Phase shifts and resonances for electron scattering by He+ below the N = 2 threshold. Physical Review A, 33, 824-838. doi:10.1103/PhysRevA.33.824
- Conneely, M.J. and Lipsky, L. (1978) Widths and configuration mixings of two-electron systems below the N = 2 threshold. Journal of Physics B: Atomic, Molecular and Optical Physics, 11, 4135.
- Ho, Y.K. (1991) Doubly excited 1P˚ resonances in He, Z Physics D Atoms, Molecules and Clusters, 21, 191-196. doi:10.1007/BF01426371
- Ho, Y.K. (1991) Complex-coordinate calculations for doubly excited states of two-electron atoms. Physical Review A, 23, 2137-2149. doi:10.1103/PhysRevA.23.2137
- Chung, K.T. and Lin, C.D. (1998) Doubly excited states of Li+ below the N = 2 and N= 3 thresholds of Li2+, Atomic Data and Nuclear Data Tables, 69, 101-124. doi:10.1006/adnd.1998.0772
- Ivanov, A.I. and Safronova, I.U. (1993) Calculation of the correlation part of the energy of two-electron systems. Optika Spectrosk, 75, 516.
- Sakho, I. Konté, A. Ndao, A.S. Biaye, M. and Wagué, A. (2010) Calculations of (nl2) and (3lnl’) autoionizing states in two-electron systems. Physica Scripta, 82, 035301. doi:10.1088/0031-8949/82/03/035301
- Sakho, I. (2010) High-lying 1P˚ doubly-excited states of H− and He below the N = 3 - 13 hydrogenic thresholds. European Physical Journal D, 59, 171-177. doi:10.1140/epjd/e2010-00163-y
- Sakho, I. (2011) Screening constant by unit nuclear charge calculations of 1,3Se, 1,3P° and 1,3De intershell Rydberg states of the helium-like ions below the N = 2 hydrogenic thresholds. European Physical Journal D, 61, 267-283. doi:10.1140/epjd/e2010-10294-8
- Khar, K. and Ho, Y.K. (2006) Doubly excited inter-shell P-wave resonances of helium in weakly coupled plasma. Journal of Physics B: Atomic, Molecular and Optical Physics, 39, 2445-2453. doi:10.1088/0953-4075/39/11/010
- Sakho, I. (2010) A modification of atomic orbital theory and its application to (1snl)1Lp and (nl2) 1Lp excited states of He-like ions. Journal of Atomic and Molecular Sciences, 2,103. doi: 10.4208/jams.022510.031010a
- Sakho, I. (2010) Modified atomic orbital calculations for (1s, nl)3Lp and
 excited states of He isoelectronic sequence. Journal of Atomic and Molecular Sciences, 3, 224. doi: 10.4208/jams.042710.051510a
excited states of He isoelectronic sequence. Journal of Atomic and Molecular Sciences, 3, 224. doi: 10.4208/jams.042710.051510a - Hicks, P.J. and Comer, J. (1975) Ejected electron spectroscopy of autoionizing states excited by low energy electron impact. Journal of Physics B: Atomic, Molecular and Optical Physics, 8, 1866. doi:10.1088/0022-3700/8/11/022
- Diehl, S. Cubaynes, D. Bizau, J.-M., Wuilleumier, F.J. Kenedy, E.T. Mosnier, J.-P. and Morgan, T.J. (1999) New high-resolution measurements of doubly excited states of Li+. Journal of Physics B: Atomic, Molecular and Optical Physics, 32, 503. doi:10.1088/0953-4075/32/17/305

