Engineering
Vol.5 No.1(2013), Article ID:26540,6 pages DOI:10.4236/eng.2013.51011
Viscoelastic Effects on Unsteady Two-Dimensional and Mass Transfer of a Viscoelastic Fluid in a Porous Channel with Radiative Heat Transfer
Department of Mathematics, Rajiv Gandhi University, Itanagar, India
Email: utpaljyotidas@yahoo.co.in
Received November 12, 2012; revised December 9, 2012; accepted December 19, 2012
Keywords: Viscoelastic Fluid; First-Order Chemical Reaction; Porous Wall; Oscillating Channel; Radiative Heat Transfer
ABSTRACT
An analysis of oscillatory flow of a viscoelastic fluid and mass transfer along a porous oscillating channel with radiative heat transfer in presence of first-order chemical reaction is considered. The problem is concerned with the flow through a channel in which the viscoelastic fluid is injected on one boundary of the channel with a constant velocity, while it is sucked off at the other boundary with the same velocity. The two boundaries are considered to be in close contact with the two plates placed parallel to each other. The effect of temperature oscillations at the plate (upper wall) where the suction takes place is taken into consideration. The plates are supposed to be oscillating with a given velocity in their own planes. Analytical expressions for velocity profile, the temperature, concentration profile, wall shear stress on the upper wall are obtained. The profiles of the velocity and skin friction have been presented graphically for different values of the viscoelastic parameters with the combination of the other flow parameters encountered in the problem under investigation. It is observed that velocity decrease with the increasing values of the viscoelastic parameter in comparison with Newtonian fluid. Also, the wall shear stress increase with the increasing values of the viscoelastic parameter.
1. Introduction
During past several years considerable interest has been evinced in the study of the problem of hydrodynamic flow in a porous channel with radiative heat transfer because of its various applications in physiology and in engineering devices such as blood flow in arteries, transpiration cooling of re-entry vehicles and rocket busters, cross-hatching on ablative surfaces. Pulsatile flow of a fluid in a porous channel has been investigated by Wang [1], as well as Bhuyan and Hazarika [2] by considering the periodic pressure gradient. Raptis [3] studied the unsteady free convective flow through a porous medium bounded by an infinite vertical limiting surface with constant suction and time dependent temperature. The effect of Hall current and wall temperature oscillation on convective flow in a rotating fluid through porous medium was studied by Ram [4]. On the other hand several other researchers (e.g. Makinde and Mhone [5], Prakash and Ogulu [6] as well as Mehmood and Ali [7]) investigated the effects of heat transfer in the flow of fluids. Adhikary and Misra [8] investigated the effects of porosity of the channel wall, magnetic field and radiative heat transfer on unsteady flow of an electrically conducting fluid through a channel. Ghosh [9] investigated the hydrodynamic fluctuating flow of a viscoelastic fluid in a porous channel, where the channels oscillate with a given velocity in their own planes. The effect of mass transfer on the flow past an infinite vertical oscillating plate in the presence of constant heat flux has been studied by Soundalgekar et al. [10]. Kim and Lee [11] reported an analytical study on the MHD oscillatory flow of a micropolar fluid over a vertical porous plate. Chamkha [12] studied unsteady two dimensional convective heat and mass transfer boundary layer flow of a viscous incompressible electrically conducting temperature-dependent heat absorbing fluid along a semi infinite vertical permeable moving plate with thermal and concentration buoyancy effects.
The purpose of the present work is to investigate the effects of viscoelastic parameter on unsteady two dimensional hydrodynamic flow and heat transfer of a viscoelastic fluid in a porous channel. The problem is concerned with the flow through a channel in which the fluid is injected in one plate with a constant velocity and it is sucked off by the other with the same velocity. The plates are considered to be oscillating with a given velocity in their own planes. In the upper wall the oscillation of the temperature is considered. It is assumed that the chemical reaction is of first-order. One of the most popular models for non-Newtonian fluids is the model that is called the second-order fluid or fluid of second grade. It is reasonable to use the second-order fluid model to do numerical calculations. The effects of viscoelastic parameter with the combinations of the other flow parameters have been studied thoroughly and presented graphically.
2. Mathematical Formulation
Consider the channel flow between two oscillating porous plates  and
and 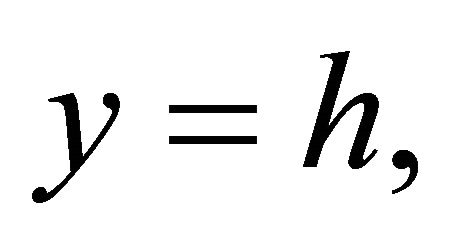 the fluid is being injected by one plate with constant velocity V and sucked off by the other plate with the same velocity. Then the continuity equation reduces to
the fluid is being injected by one plate with constant velocity V and sucked off by the other plate with the same velocity. Then the continuity equation reduces to  so that
so that  is the function of
is the function of 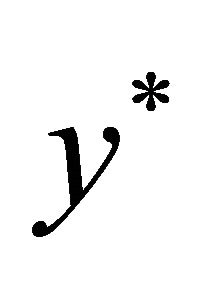 and
and 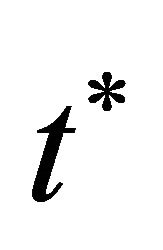 only.
only.
The constitutive equation for the incompressible secondorder fluid is
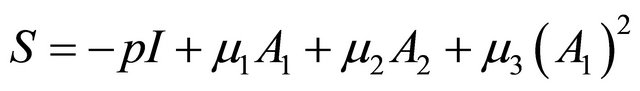 (1)
(1)
where S is the stress tensor, 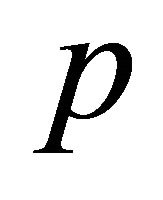 is the hydrostatic pressure,
is the hydrostatic pressure, 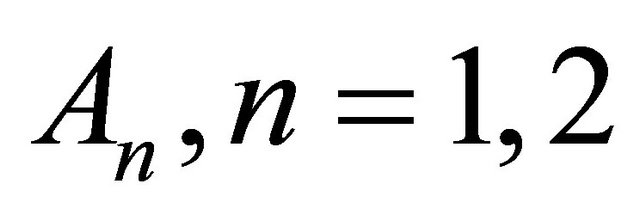 are the kinematic Rivlin-Ericksen tensors,
are the kinematic Rivlin-Ericksen tensors,  are the material co-efficients describing the viscosity, visco-elasticity and cross-viscosity respectively, where
are the material co-efficients describing the viscosity, visco-elasticity and cross-viscosity respectively, where  and
and 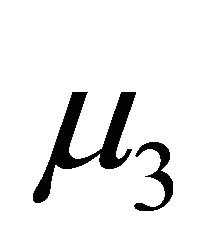 are positive and
are positive and 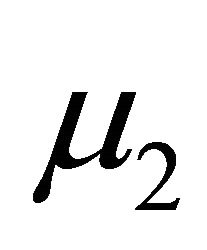 is negative (Coleman and Markovitz [13]). The Equation (1) was derived by Coleman and Noll [14] from that of the simple fluids by assuming that the stress is more sensitive to the recent deformation than to the deformation that occurred in the distant past.
is negative (Coleman and Markovitz [13]). The Equation (1) was derived by Coleman and Noll [14] from that of the simple fluids by assuming that the stress is more sensitive to the recent deformation than to the deformation that occurred in the distant past.
The momentum equations are given by
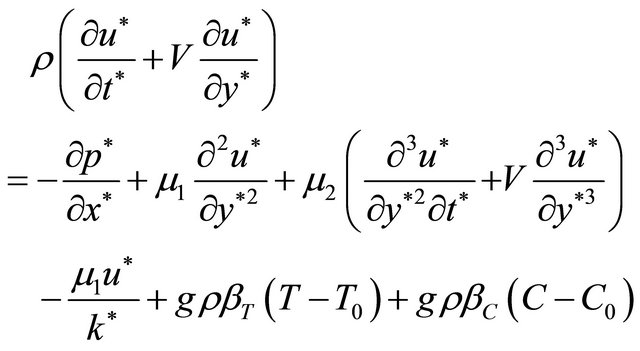 (2)
(2)
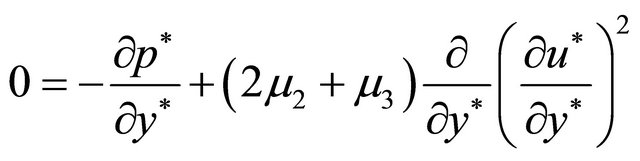
so that 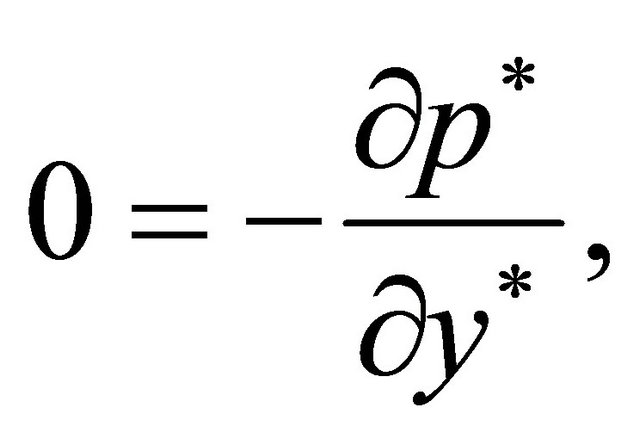 assuming
assuming 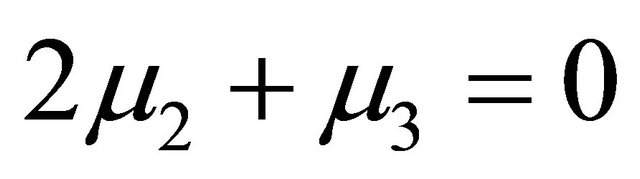 as
as 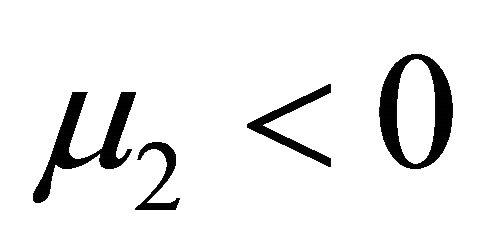
and
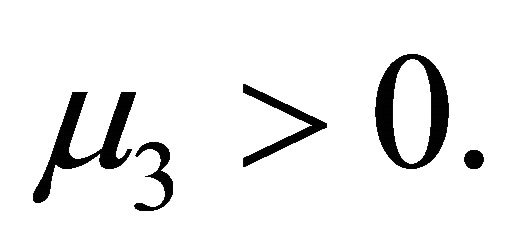 (3)
(3)
The heat transfer equation may be put in the form
 (4)
(4)
The concentration equation may be put in the form
 (5)
(5)
where 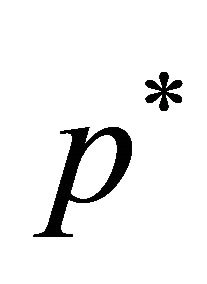 is the pressure,
is the pressure, 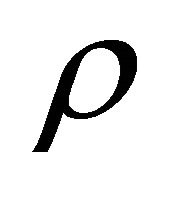 the density of the fluid,
the density of the fluid, 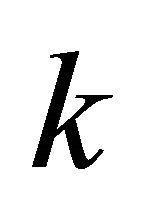 permeability factor,
permeability factor, 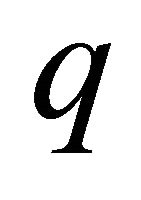 the radiative heat flux,
the radiative heat flux, 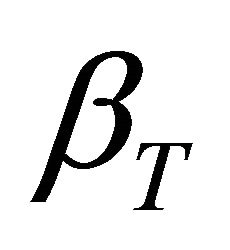 the coefficient of volume expansion due to temperature,
the coefficient of volume expansion due to temperature,  the coefficient of volume expansion due to concentration,
the coefficient of volume expansion due to concentration, 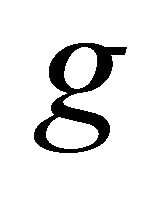 the gravitational acceleration,
the gravitational acceleration,  the coefficient of thermal conductivity,
the coefficient of thermal conductivity, 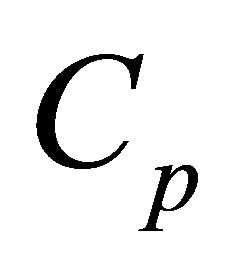 the specific heat at constant pressure,
the specific heat at constant pressure,  the concentration of species,
the concentration of species, 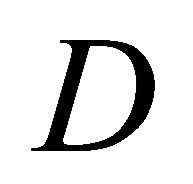 chemical molecular diffusivity.
chemical molecular diffusivity.
The corresponding boundary conditions of the oscillatory motion are:
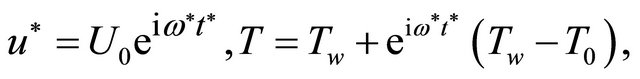
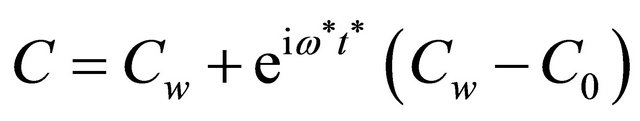 at
at 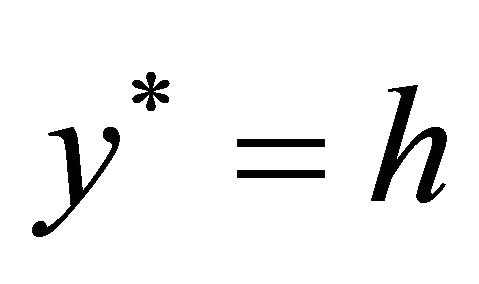
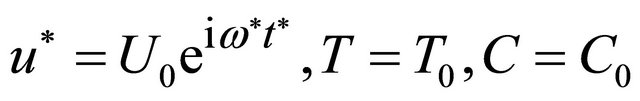 at
at 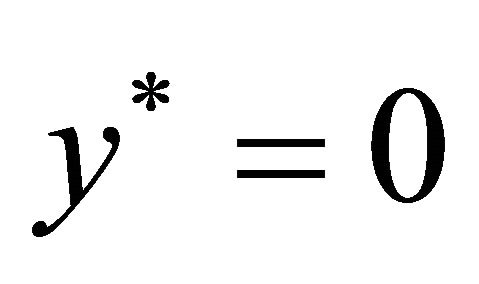 (6)
(6)
In these equations, we have taken into account the temperature oscillation on the upper plate , while the lower plate
, while the lower plate 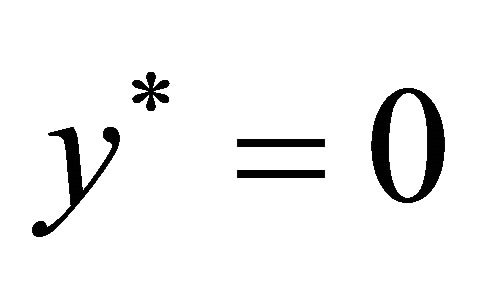 is maintained at the fixed temperature
is maintained at the fixed temperature 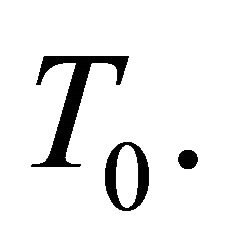
The heat flux may be expressed (Cogley et al. [15]) as
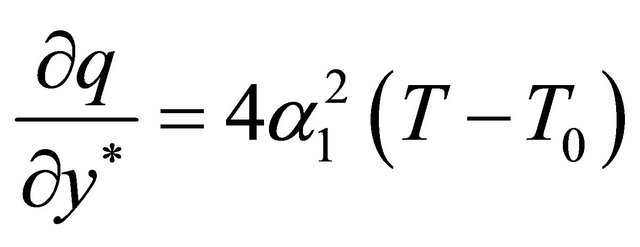 (7)
(7)
where 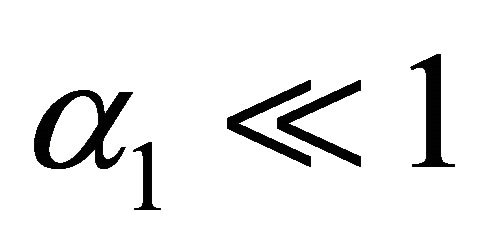 is the mean radiation absorption coefficient.
is the mean radiation absorption coefficient.
In order to write the governing equations and the boundary conditions in dimensionless form, the following non-dimensional quantities are introduced.
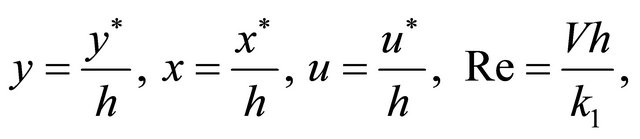

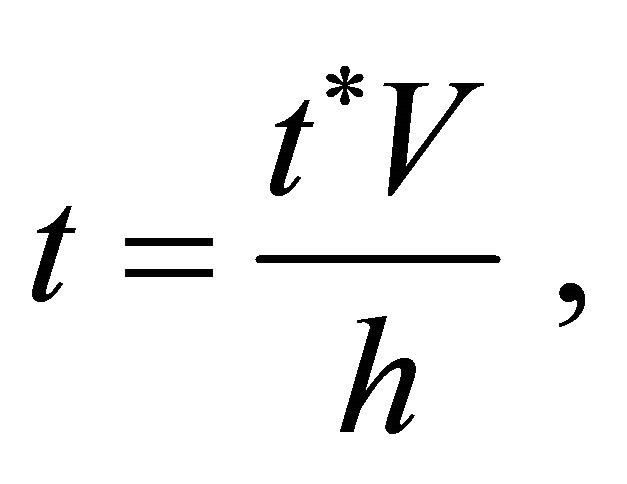

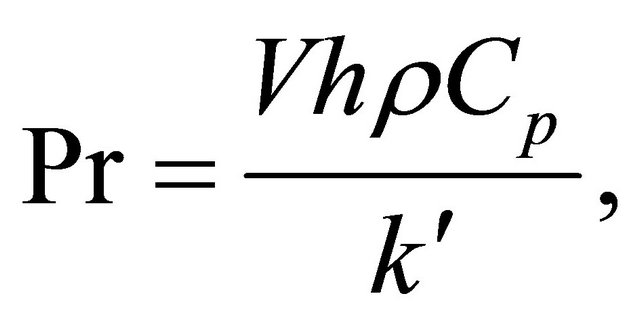
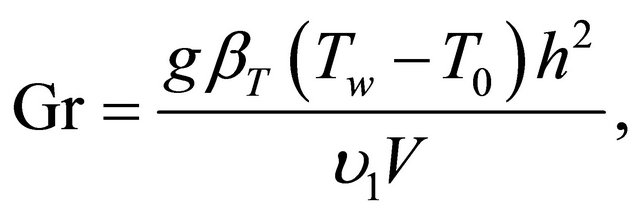

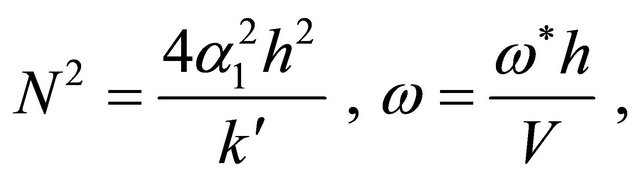
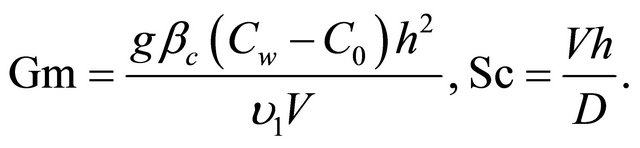 (8)
(8)
where  the Reynolds number, Gr the Grashof number for heat transfer,
the Reynolds number, Gr the Grashof number for heat transfer,  the Prandtl number, N the radiation Parameter,
the Prandtl number, N the radiation Parameter,  the angular frequency,
the angular frequency, 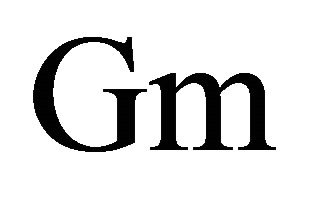 the Grashof number for mass transfer, Sc the Schmidt number.
the Grashof number for mass transfer, Sc the Schmidt number.
In view of Equations (7) and (8), Equations (2)-(4) and (5) reduce to the following dimensionless form:
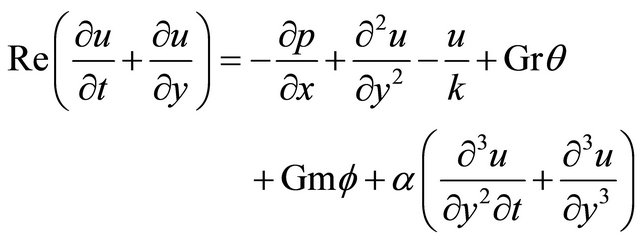 (9)
(9)
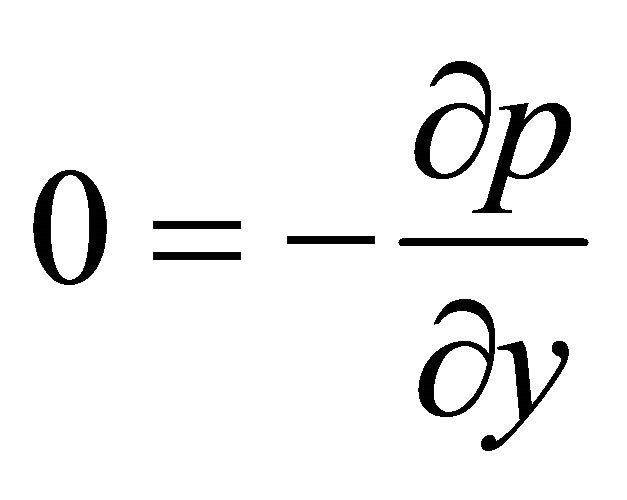 (10)
(10)
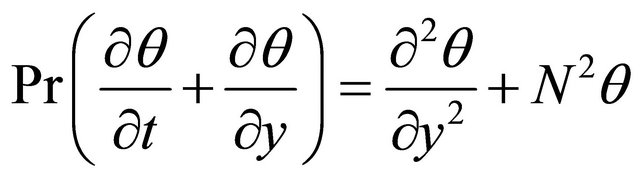 (11)
(11)
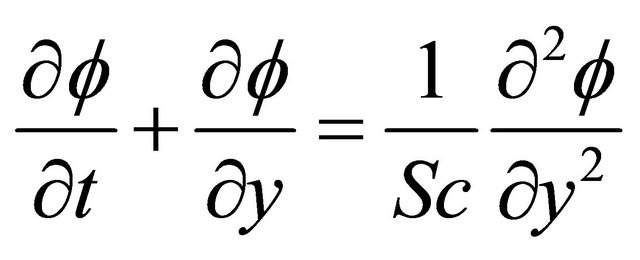 (12)
(12)
The corresponding dimensionless boundary conditions are:
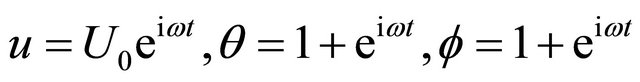 at
at 
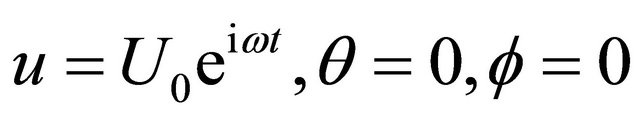 at
at  (13)
(13)
where 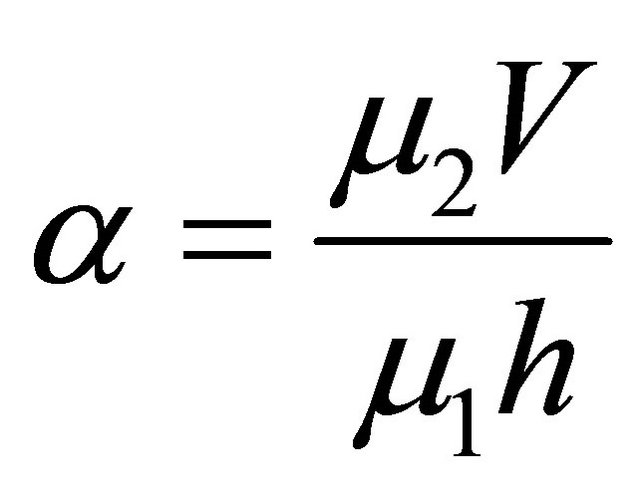 is the viscoelastic parameter.
is the viscoelastic parameter.
3. Method of Solution
From (9) and (10), it follows that  is a function of
is a function of 
alone. For the present study, we consider
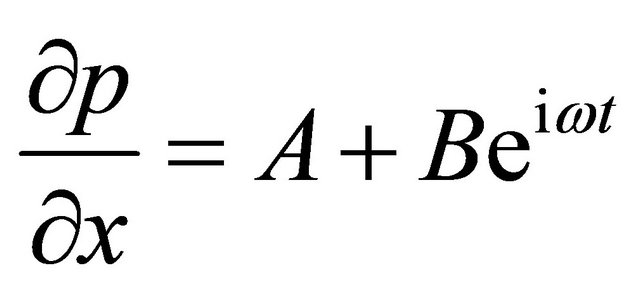 , (14)
, (14)
A and B being undetermined constants. To solve Equations (9), (11) and (12) subject to boundary conditions (13), we write the velocity, temperature, and concentration in the form
 (15)
(15)
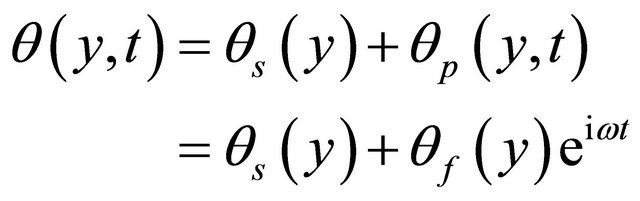 (16)
(16)
and
 (17)
(17)
where 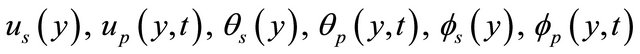 respectively represent the steady and unsteady parts of the velocity, temperature and concentration.
respectively represent the steady and unsteady parts of the velocity, temperature and concentration.
Substituting the above expressions in (9), (11) and (12) and comparing the like terms, we have derived the equations that govern the corresponding steady and unsteady flow and heat transfer of the problem under consideration. They are given below:
Steady Case:
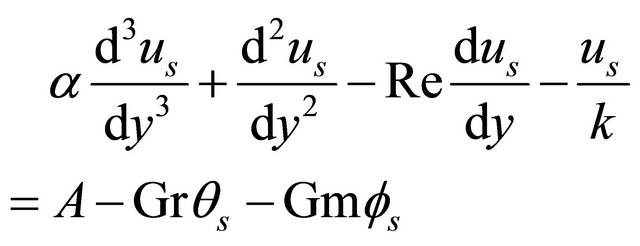 (18)
(18)
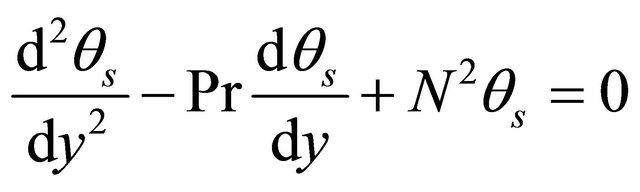 (19)
(19)
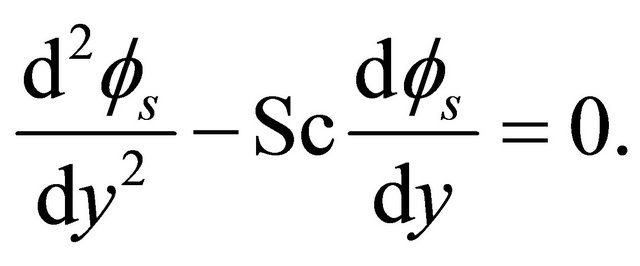 (20)
(20)
with the boundary conditions:
 at
at 
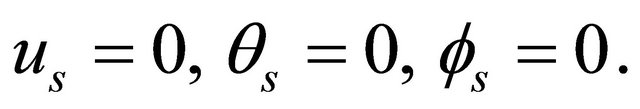 at
at 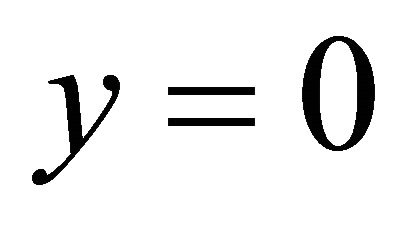 (21)
(21)
Unsteady Case:
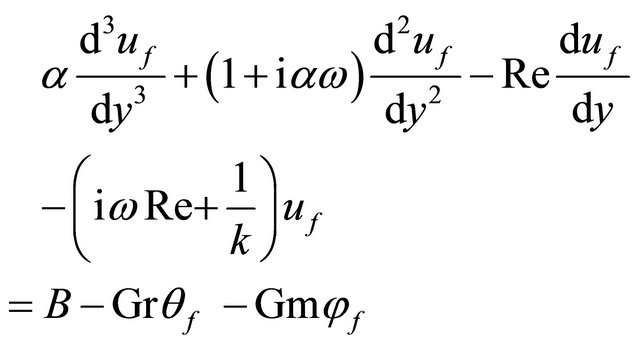 (22)
(22)
 (23)
(23)
 (24)
(24)
with the boundary conditions:
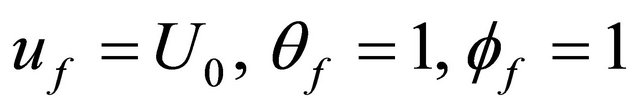 at
at 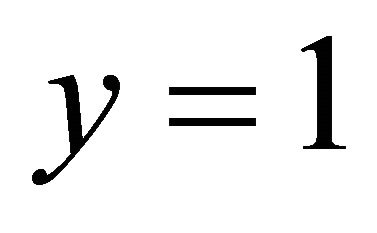
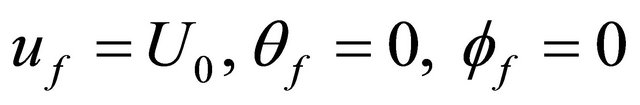 at
at  (25)
(25)
On solving the Equations (19), (20), (23) and (24) along with the boundary conditions (20) and (24), are found as
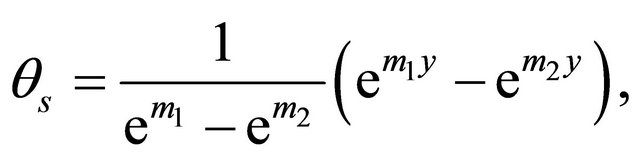 (26)
(26)
 (27)
(27)
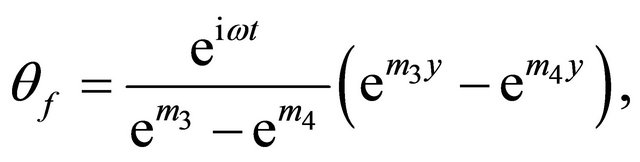 (28)
(28)
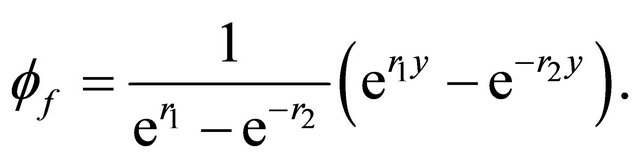 (29)
(29)
where



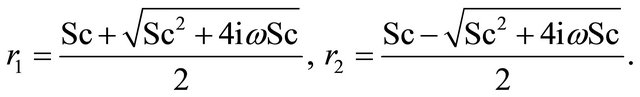
We note that 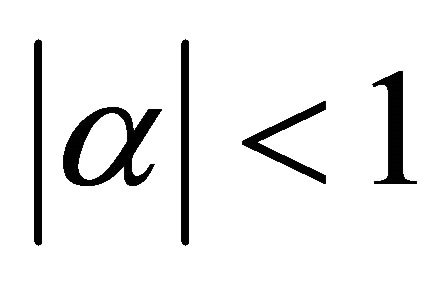 for small shear rate and so we can assume the following:
for small shear rate and so we can assume the following:
For steady case

and for unsteady case
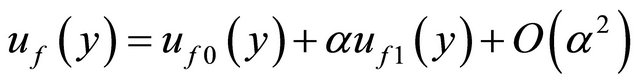 (30)
(30)
Substituting (30) in (18) and (22) together with boundary conditions (21) and (25) up to first order of 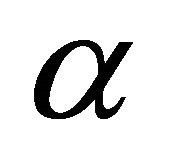 and equating the co-efficient of like powers of
and equating the co-efficient of like powers of , we obtain the following sets of ordinary differential equations and corresponding boundary conditions:
, we obtain the following sets of ordinary differential equations and corresponding boundary conditions:
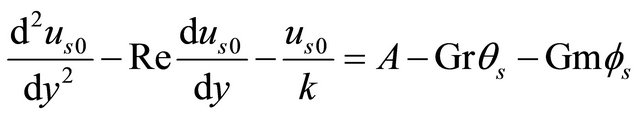 (31)
(31)
 (32)
(32)
with
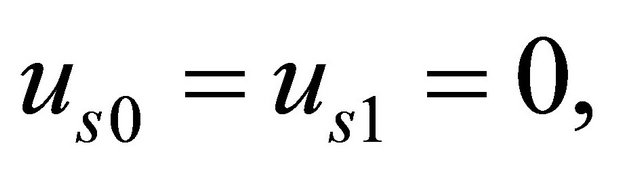 at
at 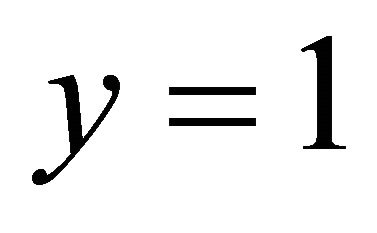
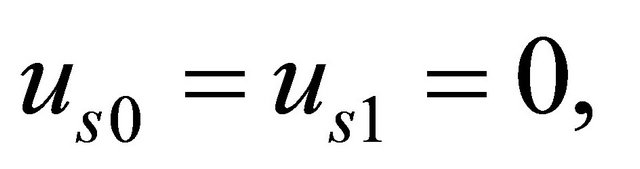 at
at 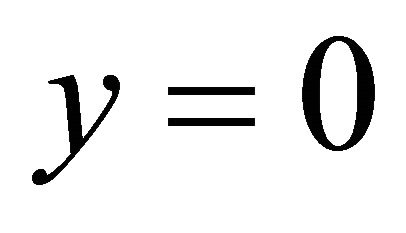 (33)
(33)
and
 (34)
(34)
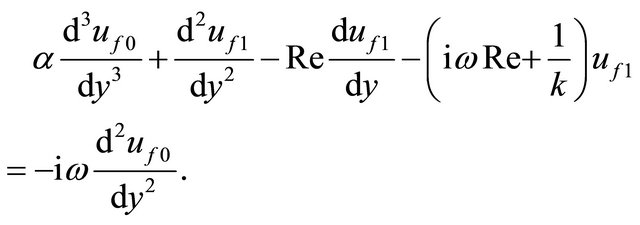 (35)
(35)
with
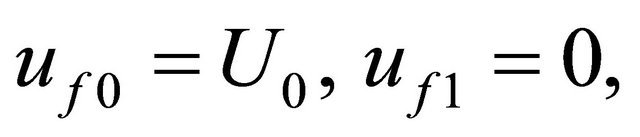 at
at 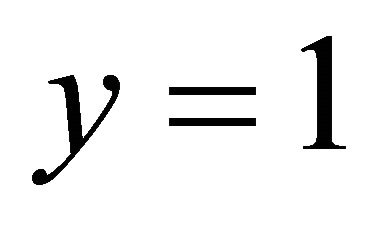
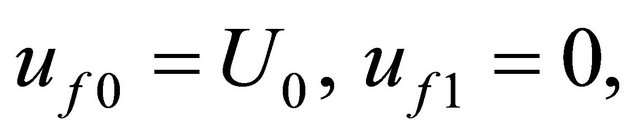 at
at 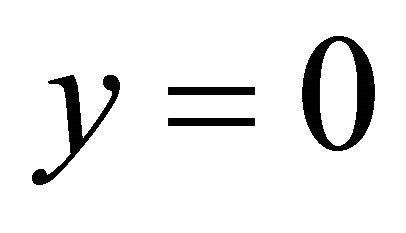 (36)
(36)
The Equations (31), (32) and (34), (35) are solved under the boundary conditions (33) and (36) respectively. Substituting these solutions in (30), we get the expressions for  and
and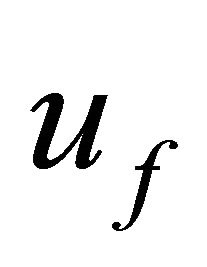 , and thus the expression for
, and thus the expression for  but due brevity the solutions are not presented here.
but due brevity the solutions are not presented here.
Nusselt number: From the temperature field, the rate of heat transfer coefficient can be obtained, which in terms of Nusselt number 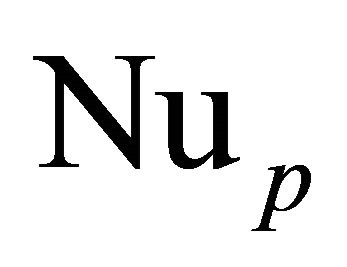 across the upper wall is given by
across the upper wall is given by
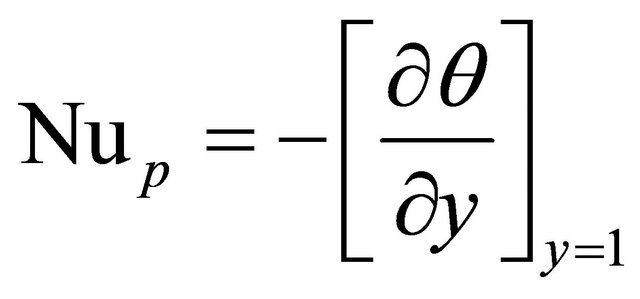 (37)
(37)
Skin-friction: Knowing the velocity field, the expression for the non-dimensional wall shear stress at the upper plate is given by
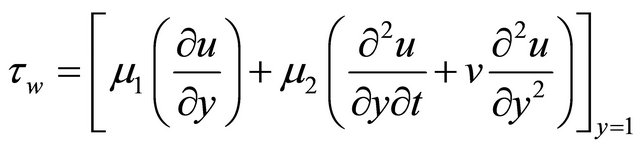 (38)
(38)
Sherwood number: From the concentration field, the rate of mass transfer coefficient in terms of Sherwood number 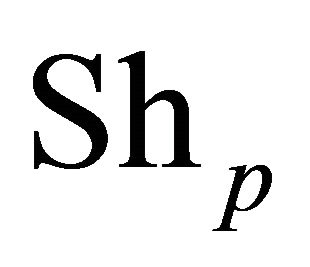 across the upper wall is given by
across the upper wall is given by
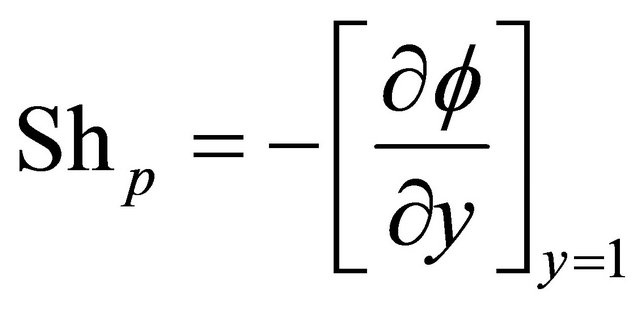 (39)
(39)
4. Results and Discussion
The purpose of this study is to bring out the effects of viscoelastic parameter 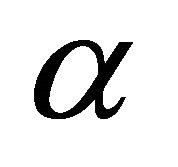 on the governing flow. The effects of viscoelastic parameter on the fluctuation of axial velocity distribution, shear stress, heat transfer, concentration profiles are evaluated numerically. The predicted variation of fluctuation of the axial velocity with different values of
on the governing flow. The effects of viscoelastic parameter on the fluctuation of axial velocity distribution, shear stress, heat transfer, concentration profiles are evaluated numerically. The predicted variation of fluctuation of the axial velocity with different values of 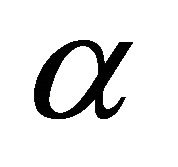 and for porous permeability parameter
and for porous permeability parameter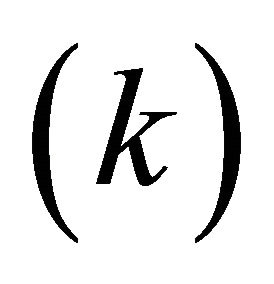 , mass Grashof number
, mass Grashof number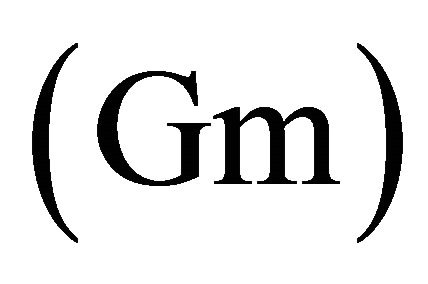 , radiation parameter
, radiation parameter  with fixed values of
with fixed values of 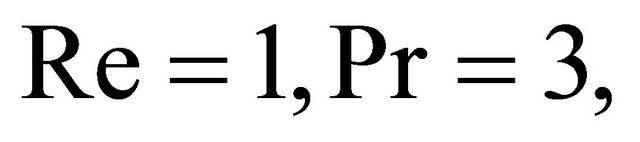
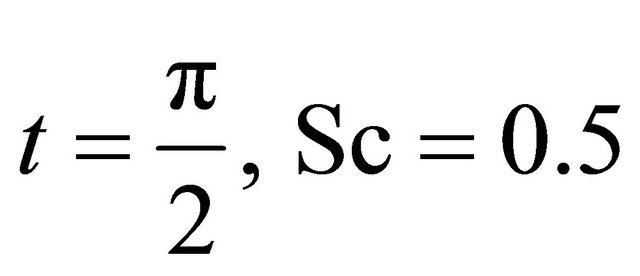 are shown in Figures 1-3. From the Figures 1-3, it is observed that the fluctuation of axial velocity is parabolic in nature and the values of
are shown in Figures 1-3. From the Figures 1-3, it is observed that the fluctuation of axial velocity is parabolic in nature and the values of  decrease with the increasing values of the viscoelastic parameter
decrease with the increasing values of the viscoelastic parameter 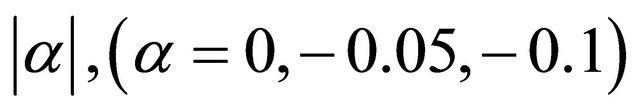 in comparison with Newtonian fluid. It is observed that the axial velocity
in comparison with Newtonian fluid. It is observed that the axial velocity  increase with the increase of permeability parameter (Figure 1), mass Grashof number (Figure 2) and radiation parameter (Figure 3) for both Newtonian and nonNewtonian cases.
increase with the increase of permeability parameter (Figure 1), mass Grashof number (Figure 2) and radiation parameter (Figure 3) for both Newtonian and nonNewtonian cases.
The wall shear stress is calculated from the Equation (38). Figure 4 shows that the wall shear stress  increases as the values of the viscoelastic parameter
increases as the values of the viscoelastic parameter 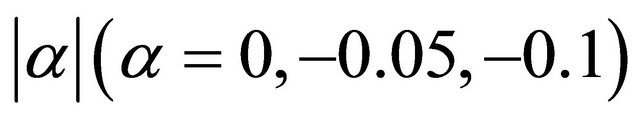 increase in comparison to Newtonian fluid. Also, the wall shear stress at the upper plate increase with the increase of mass Grashof number for both Newtonian and non-Newtonian cases.
increase in comparison to Newtonian fluid. Also, the wall shear stress at the upper plate increase with the increase of mass Grashof number for both Newtonian and non-Newtonian cases.
The temperature and concentration profiles are calculated from the Equations (37) and (39) respectively. It is observed that the temperature and concentration profiles are not significantly affected by the viscoelasic parameter.

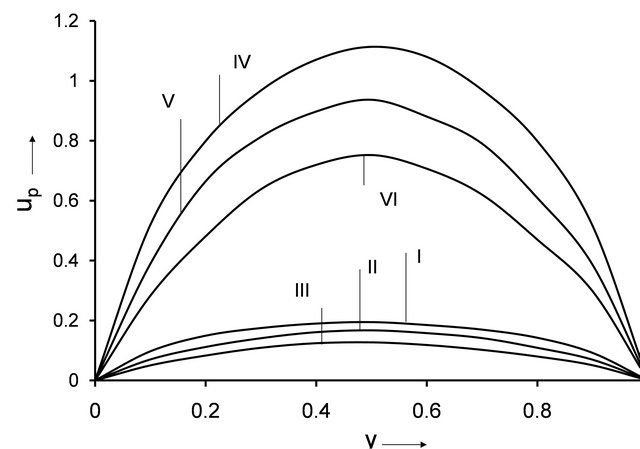
Figure 1. Variation of u against y.

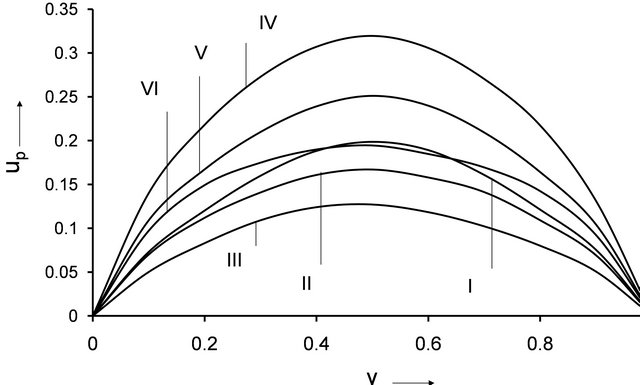
Figure 2. Variation of u against y.
5. Conclusions
The governing equations for unsteady heat and mass transfer flow of chemically reacting viscoelastic fluid through a channel with radiative heat transfer were formulated. The plates were supposed to be oscillating with a given velocity in their own planes. The effect of viscoelastic parameter of the fluid on the governing flow were analysed for various values of parameters under consideration. The conclusions of the study are as follows:

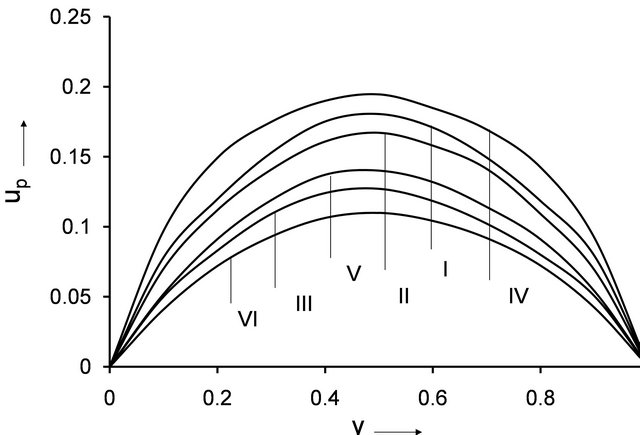
Figure 3. Variation of u against y.

Figure 4. Wall shear stress versus N when t = π.
1) Velocity decrease with the increasing values of the viscoelastic parameter in comparison with Newtonian fluid;
2) Velocity increases significantly with increasing permeability parameter and mass Grashof number as compared to radiation parameter for both Newtonian and non-Newtonian cases;
3) Wall shear stress increase with the increasing values of the viscoelastic parameter;
4) Temperature and concentration profiles are not significantly affected by the viscoelastic parameter.
REFERENCES
- C. Y. Wang, “Pulsatile Flow in a Porous Channel,” Journal of Applied Mechanics, Vol. 38, No. 2, 1971, pp. 553- 555. doi:10.1115/1.3408822
- B. C. Bhuyan and G. C. Hazarika, “Effect of Magnetic Field on Pulsatile Flow Blood in a Porous Channel,” BioScience Research Bulletin, Vol. 17, No. 2, 2001, pp. 105- 112.
- A. Raptis, “Unsteady Free Convective Flow and Mass Transfer through a Porous Medium Bounded by an Infinite Vertical Limiting Surface with Constant Suction and Time-Dependent Temperature,” International Journal of Energy Research, Vol. 7, No. 4, 1983, pp. 385-389. doi:10.1002/er.4440070409
- P. C. Ram, “Effect of Hall Current and Wall Temperature Oscillation on Convective Flow in a Rotating Fluid through Porous Medium,” Heat and Mass Transfer, Vol. 25, No. 4, 1990, pp. 205-208.
- O. D. Makinde and P. Y. Mhone, “Heat Transfer to MHD Oscillatory Flow in a Channel Filled with Porous Medium,” Romanian Journal Physics, Vol. 20, 2005, pp. 931-938.
- J. Prakash and A. Ogulu, “A Study of Pulsatile Blood Flow Modeled as a Power Law Fluid in a Constricted Tube,” International Communications in Heat and Mass Transfer, Vol. 34, No. 6, 2007, pp. 762-768.
- A. Mehmood and A. Ali, “The Effect of Slip Condition on Unsteady MHD Oscillatory Flow of a Viscoelastic Fluid in a Planar Channel,” Romanian Journal Physics, Vol. 52, 2007, pp. 85-91.
- S. D. Adhikary and J. C. Misra, “Unsteady Two-Dimensional Hydromagnetic Flow and Heat Transfer of a Fluid,” International Journal of Applied Mathematics and Mechanics, Vol. 7, No. 4, 2011, pp. 1-20.
- S. K. Ghosh, “Hydromagnetic Fluctuating Flow of a Viscoelastic Fluid in a Porous Channel,” Journal of Applied Mechanics, Vol. 74, No. 2, 2007, pp. 177-180. doi:10.1115/1.2062828
- V. M. Soundalgekar, R. M. Lahurikar, S. G. Pohanerkar and N. S. Birajdar, “Effects of Mass Transfer on the Flow Past an Oscillating Infinite Vertical Plate with Constant Heat Flux,” Thermophysics and Aero Mechanics, Vol. 1, 1994, pp. 119-124.
- Y. J. Kim and J. C. Lee, “Analytical Studies on MHD Oscillatory Flow of a Micropolar Fluid over a Vertical Porous Plate,” Surface and Coating Technology, Vol. 171, No. 1-3, 2003, pp. 187-193. doi:10.1016/S0257-8972(03)00268-8
- A. J. Chamkha, “Unsteady MHD Convective Heat and Mass Transfer Past a Semi-Infinite Vertical Permeable Moving Plate with Heat Absorption,” International Journal of Engineering Sciences, Vol. 42, No. 2, 2004, pp. 217-230. doi:10.1016/S0020-7225(03)00285-4
- B. D. Coleman and H. Markovitz, “Incompressible Second-Order Fluids,” Advances in Applied Mechanics, Vol. 8, 1964, pp. 69-101. doi:10.1016/S0065-2156(08)70353-3
- B. D. Coleman and W. Noll, “An Approximation Theorem for Functionals with Applications in Continuum Mechanics,” Archive for Rational Mechanics Analysis, Vol. 6, No. 1, 1960, pp. 355-374. doi:10.1007/BF00276168
- A. C. L. Cogley, W. G. Vincenti and E. S. Giles, “Differential Approximation for Radiative Heat Transfer in a Non-Linear Equation Grey Gas near Equilibrium,” AIAA Journal, Vol. 6, 2007, pp. 551-553.

