Engineering
Vol. 3 No. 12 (2011) , Article ID: 9215 , 9 pages DOI:10.4236/eng.2011.312152
Slip Line Field Solution for Second Pass in Lubricated 4-High Reversing Cold Rolling Sheet Mill
Department of Mechanical Engineering, University of Ibadan, Ibadan, Nigeria
E-mail: *oluwoleo2@asme.org, yinka.olaogun@yahoo.com
Received October 20, 2011; revised November 10, 2011; accepted November 20, 2011
Keywords: Slip Line Field (slf), Strip Cold Rolling, Rigid Plastic Model, Hencky’s Equation
ABSTRACT
The development of a possible slip line field (slf) for theoretical calculations of the deforming pressure (load) in a second pass of a lubricated cold rolling sheet mill and validation using values from an aluminium sheet rolling mill was done in this work. This will be relevant in the manufacturing industries providing an easy method for determining necessary applied rolling load. Experimental rolling was carried out to observe the shear lines in the deformation field. Construction of possible slip line field model was developed adhering strictly to assumptions of rigid plastic model. Calculation of the deforming force/load was achieved using Hencky’s equation. Results showed that the load calculations for constructed slip line field using aluminium sheet rolling as an example tallied with values obtained from Tower Aluminium rolling mill. Slip line fields constructed for the second pass described adequately the rolling pressure in the cold rolling process, giving a valid solution of the exact load estimates on comparison with the industrial load values. Roll pressure along the arc of contact rose fairly linearly from the entrance to a maximum at the exit point. This work showed that slf for the first pass in a cold rolling mill cannot be used for subsequent passes; it requires construction of slfs for each pass in the cold rolling process.
1. Introduction
The rolling process is one of the most popular processes in manufacturing industries, such that almost 80 percent of metallic equipment has been exposed to rolling at least one time in their production period.
Being the most wide spread metal forming process, rolling has received intensive attention from mechanical engineers. Various models are employed for the mechanical study of strip rolling processes such as the slab or force balance methods, bounding approaches, slip line field analyses and finite element method.
In comparison with other methods for analyzing the rolling process, the slip line field method is the largest class of solutions to boundary value problems in plasticity which gives exact solutions. Exact solutions require that both stress equilibrium and a geometrically self consistent pattern of flow are satisfied simultaneously everywhere throughout the deforming body and in its surfaces.
The general theory for the flow of plastic rigid material under plane strain conditions is now well established, and experimental confirmation of the validity of the theoretical equations has been obtained for many modes of deformation.
One of the few deformation processes of primary importance which occurs under almost ideal plane strain conditions is that of rolling. Several analyses have been published in literature. The mechanics of rolling can be traced back to 1925 by T. Von Karman [1]; he suggested the theory of homogenous deformation based on simplified equilibrium of forces acting on a slab element in the deformation zone of strip. Orowan [2] discarded the assumption of homogeneous deformation and developed a theory of homogeneous deformation. The differential equation for slab element was derived under various assumptions and approximations [3-5]. A slip-line field solution for hot rolling was presented by Alexander [6]. Further slip-line field solutions for cold rolling with friction were suggested by Firbank and Lancaster [7] for small rolls only and a pass reduction of 20% and later slip-line fields for lubricated cold-rolling were proposed for 20 in Dia rolls with sheet reduction of 25% [8]. Work on slip-line field solutions for compression and rolling with slipping friction was also done by Collins [9].
Dewhurst and Collins [10] suggested a matrix technique for the construction of slip line fields and illustrated the technique with reference to strip rolling and drawing. However, there is lack of information on slip line field solutions to subsequent passes after the first pass in cold rolling mills which will be quite relevant in the cold rolling firm.
2. Review of Numerical Techniques for Solving Forming Processes
2.1. The Slab Method
The slab method is approached from the elementary theory of the free body equilibrium [11]. The technique relies on dividing the work piece into a number of finite regions (strips, slabs, disks), the geometry of which depends on the nature of the problem. Each region is placed in force equilibrium. The method usually invokes the Tresca yield criterion and considers the material to be non-hardening (although allowance for work hardening can be made in an approximate manner by using a mean value of yield stress). It also permits an account to be taken of either Coulomb or constant shearing friction, it is to be noted that friction has often been treated as an adjustable parameter in order to provide the best correlation between theoretical predictions and experimental results.
The method can also be used to estimate forging loads for quite complex forgings. The work piece is divided into a number of modules, each of which is analyzed separately and then recombined to provide estimate of the forging load.
The slab method provides an unrealistic representation of the stress distribution within the deforming material because it is only obtained as a one-dimensional distribution. No account is taken of the in homogeneity of deformation, temperature and strain rate effects.
2.2. The Bounding Methods
Two extremum principles due to Hill [12] can be used to obtain “upper” and “lower” bounds for the loads to cause plastic flow. The practical applications of these princeples have generally been restricted to rigid non-hardening solids deforming under plane strain conditions.
2.2.1. Upper Bound Method
As the name implies, the technique provides an over estimate of the load(s) to effect plastic flow. The usual procedure is to divide the deformation region into a number of finite zones. The material moves as a rigid mass within each zone to another. The bounding lines are usually straight and a discontuity in the tangential component of velocity occurs across each of these lines. From the pattern of discontuity lines in the “physical plane” a corresponding velocity diagram (or Hodograph) can be constructed. Certain velocity boundary conditions have to be satisfied, but no attempt is made to ensure that the material in each zone satisfies a yield criterion and there is no requirement that the individual zones are to be in equilibrium with each other. The rate of external working of the unknown traction (or load) is equated to the internal energy dissipated as material is sheared across each of the discontinuity lines. The method is usually adopted in the study of metal working problems since it provides an overestimate of the energy requirements to be delivered by a machine or press in order to execute the forming process.
2.2.2. Lower Bound Method
Here again the material is divided up into a number of finite zones, similar to the discontinuity line pattern in the Upper Bound Method. However, in this case the emphasis is on establishing a statically admissible stress field (as opposed to a kinematically admissible velocity field). Each zone is placed in force equilibrium with its neighbor and it is stipulated that no zone has to exceed the yield criterion (the Tresca and Von Mises criteria take the same form under plane strain conditions). The unknown surface tractions are revealed through the equilibrium stress field.
The technique is often applied to structural analyses since it provides an underestimate of the load to cause plastic collapse.
It is to be noted that in general the Upper Bound and Lower Bound methods do not reveal a unique solution. However, adjustments can be made to the shape of the individual zones to reveal the lowest Upper Bound and the highest Lower Bound solution, for a basic zone pattern.
Upper Bound solutions far outweigh Lower Bound solutions in metalworking studies. The text by Avitzur [13] placed emphasis on Upper Bound Methods for other than plane strain deformation problems.
2.3. Slip Line Field Theory
Slip line field theory has been most widely applied in the study of plane strain deformation of rigid, non-hardening, solids [14,15]. It contains features of both the Upper and Lower Bound methods, in that it permits a kinematically admissible velocity field along with a statically admissible stress field which satisfies the yielding condition within the deformation zone. It follows that the solutions obtained by the Upper and Lower Bound methods straddle (or bound from above and below) the slip line field solution.
The governing stress and velocity equations are hyperbolic and can be solved by the method of characteristics. It transpires that the characteristics for stress and velocity are identical and they lie in the direction of the maximum shear stress. Hence the deformation zone is covered by a network of orthogonal characteristics, and these are commonly referred to as the slip lines.
Many similarities appear to exist (in fact these tend to be superficial) between a slip line field and upper bound solution. In both methods the physical plane is covered by a network of lines, from which a velocity diagram can be constructed. However, with the slip line field solution the network is orthogonal (i.e. the characteristics) and furthermore not all the slip lines have a discontinuity in the tangential component of velocity across them (this is always the case with the Upper Bound Method).
In statically determinate problems the usual procedure has been to build up a pattern of slip lines (based largely on experience) and to obtain the stress distribution within the deforming zone via the so called Hencky equations, i.e. the equilibrium equations reformulated along the characteristics. It is not always possible to proceed in this manner, in which case the slip line field and the hodograph have to be constructed simultaneously. In the past, this has led to laborious trial and error procedures (usually graphical) before an acceptable solution is obtained. A recent innovation, which obviates much of the labour with trial and error methods, is the matrix operational method due to Collins [9] and its subsequent development into a systematical computational procedure by Dewhurst and Collins [10].
One of the main criticisms levelled against slip line field theory is that it treats non-hardening solids only and ignores strain-hardening, strain-rate and temperature effects. Allowance can be made for strain hardening, but the resulting stress equations along the characteristics lose their simplicity and recourse has to be made to numerical procedures to effect a solution. However, this problem may be overcome by finding slip—line fields for each strain-hardening pass. The present work is in that direction.
2.4. The Finite Element Method
The finite element method has been increasingly employed as an analytical tool in dealing with metal forming processes. The finite element method is the most practical and accurate. This approach involves the representation of a body or a structure by an assemblage of subdivisions called finite elements. These elements are interconnected at joints which are called nodes or nodal points. Simple displacement functions are chosen to approximate the distribution or variation of the actual displacement over each element; these equations, for the entire body are then obtained by combining the equations for the individual elements in such a way that continuity of displacements or forces is preserved at the intercomnecting nodes, the overall stiffness matrix for the whole body results.
When dealing with metal working operations, the analysis is formulated in terms of either elastic-plastic solid (which is usually based on the elastic-plastic stressstrain matrix developed or rigid-plastic solid.
In hot forming process the material is often treated as an incompressible non-Newtonian fluid, where the viscosity is related to the strain rate and possibly temperature and total strain.
Many models developed using the finite element method have been proposed. For example, Weroński et al. [16] worked on drop forging of a piston using slipline fields and FEM. Likewise, Mori et al., [17] used finite element method in simulating rigid-plastic planestrain rolling and Synka and Kainz, [18] used a novel mixed Eulerian-Lagrangian finite-element method for steady-state hot rolling processes.
However, in metal forming processes the interfacial frictional conditions between tools and work piece and certain boundary conditions are known imprecisely, and there is always some doubt about the appropriateness of any constitutive equation particularly when temperature and strain rates are involved. Consequently, even the most rigorous analytical procedure is controlled by the reliability of the input data.
2.5. Slip-Line Field Solution Procedure
In the absence of body forces the state of stress in a body deforming under conditions of plane strain satisfy the equilibrium Equations;

 (1)
(1)
The stress state at any point in the deforming material can be represented in Mohr circle diagram modeled by Mohr-Coulomb failure criterion. The loci of those directions of maximum shear stress and shear strain form two orthogonal families of curves known as slip lines.
From Mohrs circle, the stress can be expressed as follows:

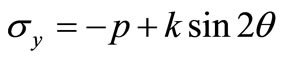
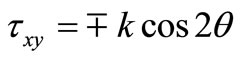 (2)
(2)
where, 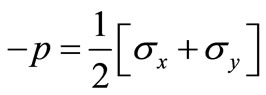 is the hydrostatic part of the stress tensor and
is the hydrostatic part of the stress tensor and 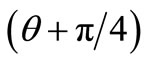 is the anti-clockwise rotation of the direction of algebraically greatest princepal stress from the positive direction of the x axis Differentiating and substituting Equation (2) in Equation (1)
is the anti-clockwise rotation of the direction of algebraically greatest princepal stress from the positive direction of the x axis Differentiating and substituting Equation (2) in Equation (1)

 (3)
(3)
Equations (3) are hyperbolic and yield two families of characteristics inclined to the x-axis at angles  and
and  respectively, thus forming an orthogonal network known as slip lines [19]. The members of the family given by the parameter
respectively, thus forming an orthogonal network known as slip lines [19]. The members of the family given by the parameter  are, by convention, called the α-lines and β-lines coincide with the trajectories of maximum shear stress.
are, by convention, called the α-lines and β-lines coincide with the trajectories of maximum shear stress.
The hydrostatic pressures along the slip lines satisfy Hencky’s equations, which in the absence of workhardening may be expressed as:
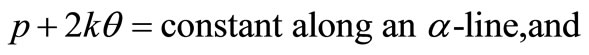
 (4)
(4)
The velocities along the slip-lines are related by Geiringer’s equations written as,

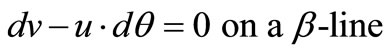 (5)
(5)
where, u and v are the velocity components in α and β directions respectively.
A field of slip-lines possesses several geometrical properties, which are enunciated in the two theorems due to Hencky [12]. Hencky’s first theorem states that the angle between two slip-lines of one family, where they are intersected by a pair of slip-lines of the other family, is constant along their length. Thus, we have
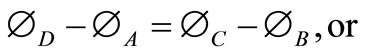
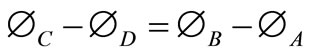 (6)
(6)
Hencky’s second theorem states that as we move along a slip-line, the radius of the slip line of the other family at the points of intersection changes by the distance traveled. Thus, the changes can be represented as
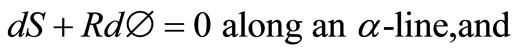
 (7)
(7)
Solution to boundary value problems by analytic integration of the plain strain equations is possible only in a few simple cases. Hence, construction of the slip line network is usually carried out by the graphical procedures [12].
3. Materials and Method
Experimental cold rolling was done by subjecting cast lead to two passes on a laboratory rolling mill. Slip line fields were constructed based on the shear line observations after which calculations of deforming pressure using slip line field equations were done. Validation was done using values obtained from Tower Aluminium Rolling Mills, OTA, Ogun State, Nigeria.
3.1. Experimental Rolling to Determine Shear Patterns
Lead alloy was used in simulating shear patterns occurring in the second pass of a cold rolling mill. The alloy was cast into a rectangular-shaped slab (180 mm by 40 mm by 14 mm) using a pattern mould, and machined into various thickness of 10 mm, 8 mm and 7 mm thickness. Each prepared thickness lead sample was subject to cold rolling on a manually operated laboratory cold rolling machine, where it was deformed into various thicknesses (8.55 mm, 5.70 mm, and 5.35 mm respectively) in two passes. The deformed zones were subjected to macroscopic examination using macro etching.
3.2. Macro Etching of Lead Samples
The macro etchant solution used for macroscopic examination was composed of water (H2O), concentrated Nitric acid (HNO3) and Molybdic acid (140 ml, 40 ml, and 30 ml respectively). The solution was mixed and placed in a glass beaker. The mixed macro etchant solution was applied on the surfaces of the lead samples for 5minutes before it was rinsed, dried and viewed under a magnifying lens Figures 1 and 2).
3.3. Construction of Slip-Line Fields for Second Pass Using Real Life Scale
The slip line field for the first pass (Figure 3) was drawn using the generalized slf for rolling [20]. The slip line field was modified for the second pass incorporating the observed shear zones (Figure 4).
3.3.1. General Procedures
Slip-line field was constructed for the first pass and compared with industry value to validate our calculation procedure. After this, the slip-line field for the second pass was developed.

Figure 1. Macro-etched lead sample with arrows showing shear lines running across plate caused by lower and upper rolls after two passes.

Figure 2. Segmented top portion of macro-etched lead sample with arrow showing shear line running across plate caused by upper roll after two passes.

*H (sheet thickness inlet) = 7.0 mm; *h (sheet thickness outlet) = 4.5 mm.
Figure 3. Constructed slip line field for 1st Pass in a cold-roll mill.
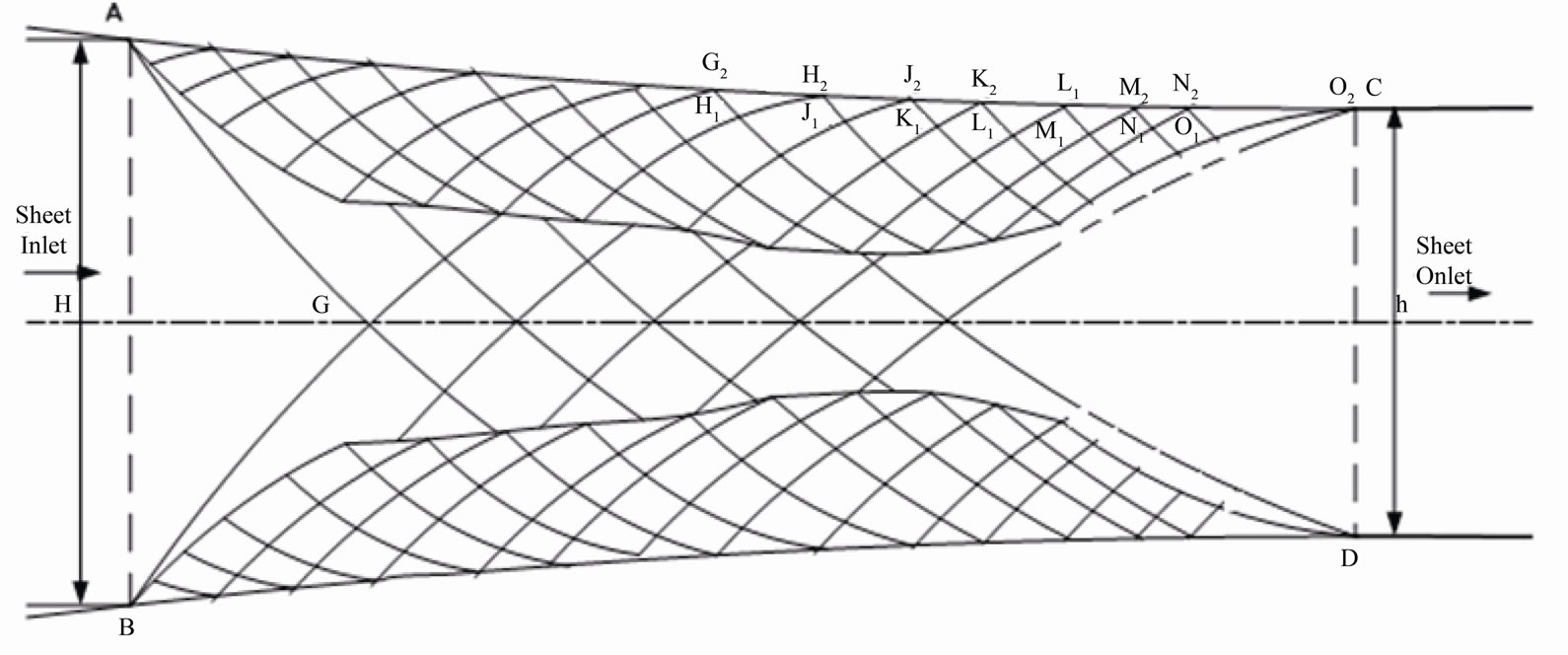
*H (sheet thickness inlet) = 4.5 mm; *h (sheet thickness outlet) = 3.4 mm.
Figure 4. Constructed slip line field for 2nd pass of a cold-roll mill.
The shear pattern observed in the simulated second pass rolling of lead was used in developing a slip-line field for the second pass in a cold-roll sheet mill. The plastic region generally consists of a number of subsidiary domains with the curvature of the slip lines changing discontinuously across their boundaries. The construction of the slip line field depends on the boundary conditions. Here, a lubricated smooth roller surface was considered conforming to lubricated cold rolling in real life practice. It is a statically determinate problem, in which the slip line field is uniquely defined by the stress boundary conditions and represents a plastically deforming zone.
The assembly of the slip line field was based on their 45˚ intersections with axes of symmetry and their reflections at stress discontinuities. In determining slip lines for interior yielding, tangents were projected to the roller boundary at various points in the plastic region. α-and β-lines were in conformity with convention that the direction of the algebraically greatest principal stress passes through the first and third quadrants of the local system. The α- and β-lines intersect at the boundary points and at their intersections, the α- and β-lines are subjected to the same hydrostatic stress.
The shear region was included in the slip-line field pattern. The shear region was considered to harbour a slipline field.
3.3.2. Assumptions and Additional Procedures Made in the Construction of slf for the Second Pass
1) It was assumed that the shear region covered the entire arc length of contact.
2) That the shear occurred as a result of slip.
3) That the shear morphology tapers to the roll surface at the end of the arc length of contact.
4) That the shear morphology is not necessarily a perfect arc but straightens out at the middle of the arc of contact due to pressure from remaining mass of unsheared material between the sheared surfaces.
5) That a whole series of new α- and β-slip lines are formed within the sheared zones bounded by the shear zone.
6) That the initial β-slip line from the slf running through the centre of the sheet must run through the shear zone and be a β-line in the upper shear zone for continuous mass movement which will not make the shear zone disjointed from the main mass of material and maintain mass movement.
3.4. Numerical Solution Procedure
3.4.1. General Procedure
The solution proceeded as follows:
1) Labeling of the α- and β-slip lines in conformity with the convention that the direction of the algebraically greatest principal stress passes through first and third quadrant of the local system.
2) Denotation of the family of slip lines that are α- and β-lines.
3) Determination of angular distortion in the slip-line field net for each point considered by measurement (The slip-line fields were drawn to scale).
4) Calculation of the normal stress at each point considering the angular distortion of each point using Hencky equations until we get to the point at the bottom of the roll.
5) Determination of the deforming force (load) by multiplication of area of contact and normal stress (pressure).
3.4.2. Additional Assumption and Procedure for Calculating Normal Stresses in the Constructed slf for the Second Pass
It was assumed that the the β-line running through the center of the sheet (i.e. BG) hits a corresponding one within the shear zone thereby running through to the roll surface. Thus, the force is transmitted along the same β- line to the roll surface can easily be calculated and linked up with slip lines in the shear zone.
The full procedure calculations for the second pass of the cold-rolling mill are placed in the appendix.
4. Results and Discussions
4.1. Results
Figure 1 shows shear lines on a lead sample after two passes of a cold-rolling operation. Figure 2 shows the top portion of another sample subjected to two passes in the cold-rolling process. Shearing is well pronounced after the second pass.
Figure 3 shows slip line fields constructed for the first pass using well known slip line field model. Input and output values of sheet thickness used were the same as in industry values Tower Aluminium rolling mills, OTA, (Nigeria).
Figure 4 shows slip line fields constructed for the second pass in a cold rolling mill showing the inclusion of the shear zones in the upper and lower segments of the sheet. Values of input and output sheet thickness were the same as that used in the Tower Aluminium rolling mills factory.
Figure 5 shows the variation of roll pressure along the arc of contact for the first and second passes.
Table 1 presents the summary of results from the slip line field calculations of normal stress (pressure) at various points on the roller surface for the first pass.
Table 2 is the presentation of slip line field calculations of normal stress (pressure) at various points on the roller surface for the second pass using the modified slip line field for rolling.
The tensile yield strength (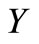 ) of Aluminium with grade Al 1200 is about 25 N/mm2. Al 1200 is the grade of Aluminium used for hollowares. Since we are considering a rigid perfectly-plastic isotropic material, shear yield strength (
) of Aluminium with grade Al 1200 is about 25 N/mm2. Al 1200 is the grade of Aluminium used for hollowares. Since we are considering a rigid perfectly-plastic isotropic material, shear yield strength (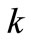 ) will have a constant value throughout the plastic region. Therefore, Tresca criterion
) will have a constant value throughout the plastic region. Therefore, Tresca criterion  is used because it does not affect the equivalent flow stress.
is used because it does not affect the equivalent flow stress.
Table 3 presents a comparison of calculations of slip line field calculations with Industrial values. It could be seen that the load values using the slf for rolling for the first pass of cold-rolling tallies exactly with industrial values. Using the same slf for calculating the second pass was seen to be non-representative as the value was way below the real value needed for deformation. However, using the modified slf constructed specifically for the second pass, the value fell within range of the real values used in industry.
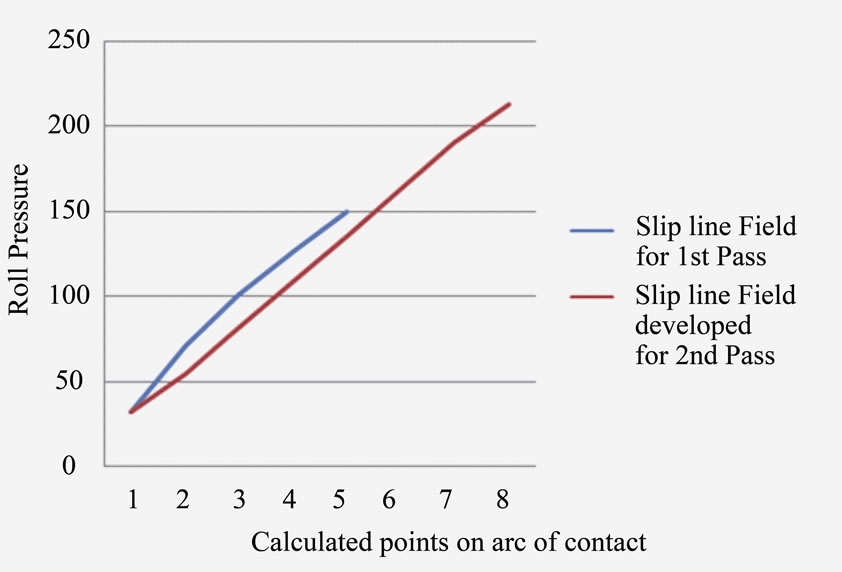
Figure 5. Distribution of the roll pressure along the arc of contact in the Slip line Field Models (Measured length of arc of contact was 17.33 mm and 12.84 mm for slf1 and slf2 respectively).
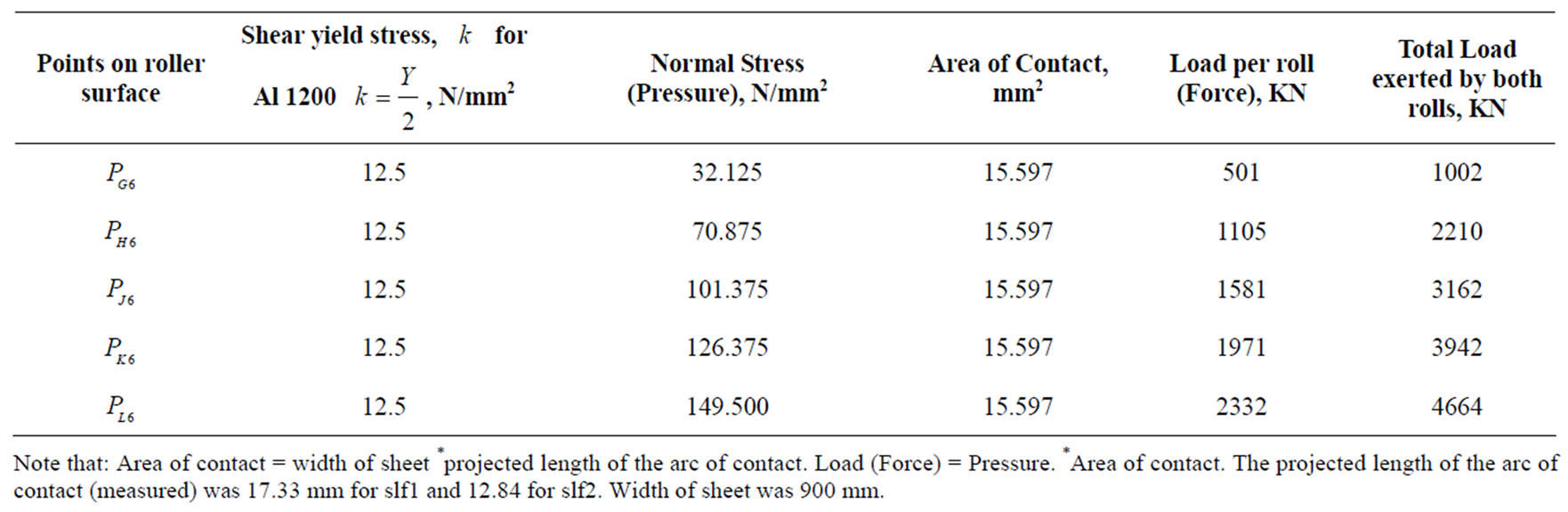
Table 1. Summary of calculated load from slip line field for 1st pass.
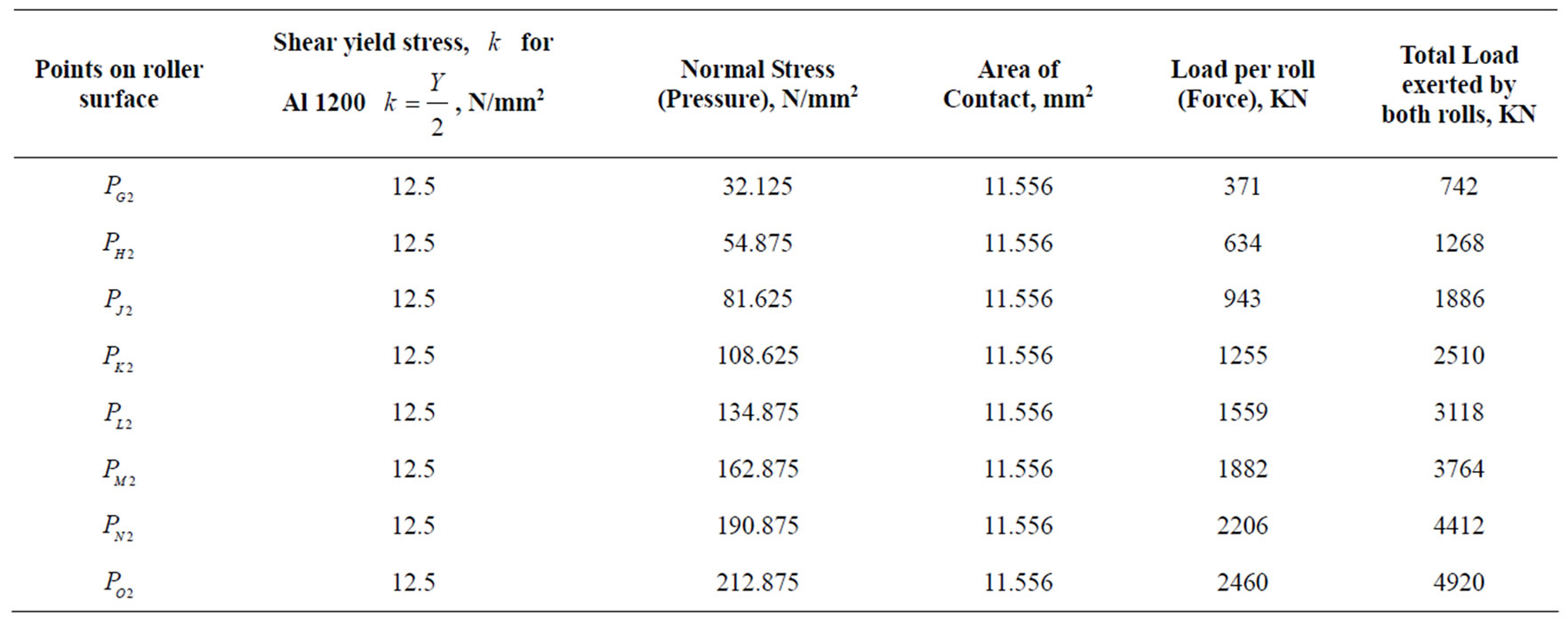
Table 2. Summary of calculated load from slip line field model for 2nd pass.
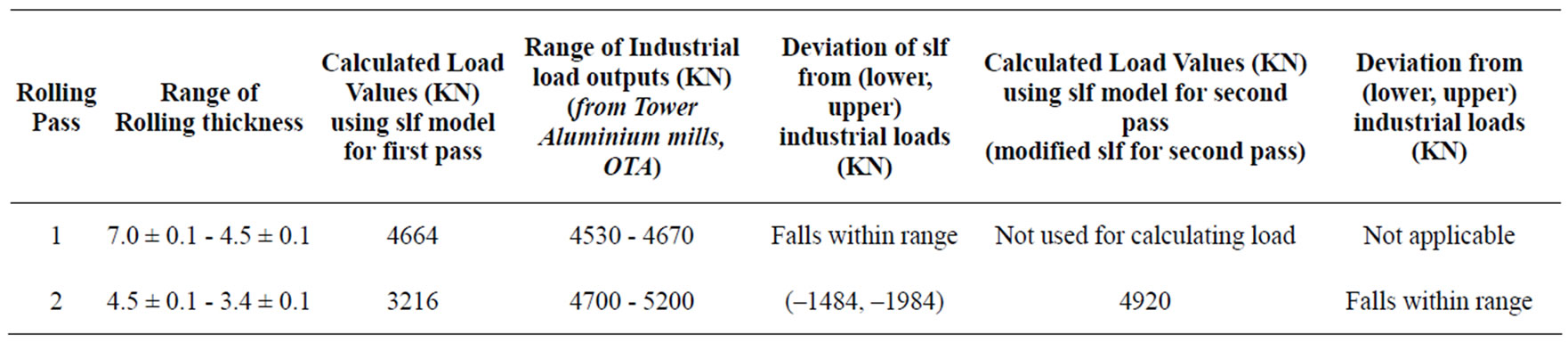
Table 3. Comparison of calculations of slip line field values with Industrial values.
4.2. Discussion
4.2.1. Shear Lines on Lead Sample after Second Pass Cold-Rolling
Figures 1 and 2 show clear shearing after the second pass rolling of lead samples. It is assumed the same deformation process observed in the cold-rolling of the lead samples will occur in metal/alloy rolling. This was applied in the constrction of a slf model for the second pass in a cold-roll mill as shown in Figure 4.
4.2.2. slf Calculations for First Pass and Comparison with Industrial Values
Figure 3 needs little introduction as it is the well known slf model for rolling. The α- and β-slip lines were constructed to scale with the input and output sheet thicknesses simulating the first pass in an industrial coldrolling process. The calculations for the rolling pressure and applied loads at each point on the roll surface could be seen in Table 1. Comparison of the calculated values to industrial values in the first pass cold-rolling process showed good tally (Table 3). This proved the usefulness of the existing slf model for determining applied loads for the first pass in a cold-rolling sheet mill.
4.2.3. Using Existing slf for Second Pass
The existing slf model was used in predicting the applied loads for the second pass in an Aluminium cold-roll mill. The result as expected fell far short of industrial load needed to cause deformation (Table 3). While the calculated value was 3216 KN, the industrial range of applied loads was 4700 - 5200 KN. This has proved again the unsuitability of the same model for the second pass in a cold-rolling sheet mill.
4.2.4. Modified slf for Second Pass
Figure 4 shows the modified SLF for the second pass in a cold-rolling sheet mill. It shows the α- and β-slip lines in the shear zones superimposed on the existing SLF model constructed using input and out-put sheet thickness values as obtained in Aluminium sheet rolling. The initial α- and β-slip lines running through the middle of the sheet were observed to cross at G. The β-slip line was assumed to run continously through the shear zone and hit the roll at G2. With these assumption already stated in the methodology, the loads were calculated and presented in Table 2. The total load was seen to be higher (4920 KN) than the load for the first pass (4664 KN) shown in Table 1 and fell within the values used in industrial Aluminium rolling for second pass (4700 - 5200 KN; Table 3). This modified slf model seems to have taken into consideration the effect of shearing which occurred on the surface of the rolled sheet during the second pass which the existing slf could not account for as revealed in Table 1.
4.2.5. Variation of Rolling Pressure with Rolling Arc Length
It was generally observed from Tables 1 and 2 that roll pressure exerted on the sheet metal increased from the point of roll surface contact at the entrance of the sheet metal (roll gap entrance) to the point of exit of the sheet (roll gap exit). At the point of exit plane of the metal sheet the roll pressure is maximum (Figure 5).
5. Conclusions
1) The distribution of the roll pressure along the arc of contact showed that the pressure rose fairly linearly to a maximum at the exit point.
2) Slip line fields must be obtained for each cold-rolling pass to get valid solutions of the exact load estimates.
3) Existing slf is valid for the first pass of a cold-rolling sheet mill alone.
4) A modified slf model for second pass in a cold-rolling sheet mill has been proposed and developed in this work which describes well the load estimates for the second pass in a cold-rolling sheet mill.
6. REFERENCES
- T. Von Karman, “On the Theory of Rolling,” Zeitschrift für Angewandte Mathematik und Mechanik, Vol. 5, 1925, pp. 130-141.
- E. Orowan, “The Calculation of Roll Pressure in Hot and Cold Flat Rolling,” Proceedings of the Institue of Mechanical Engineering, Vol. 150, 1943, pp. 140-167.
- A. Nadal, “The Force Required for Rolling Steel Strip under Tension,” Journal of Applied Mechanics ASME, Vol. 61, 1939, pp. A54-A62.
- D. R. Bland and H. Ford, “The Calculation of Roll Force and Torque in Cold Strip Rolling with Tensions,” Proceedings of the Institute of Mechanical Enigineering, Vol. 159, No. 1, 1948, pp. 144-163. doi:10.1243/PIME_PROC_1948_159_015_02
- R. B. Sims, “The Calculation of Roll Force and Torque in Hot Rolling Process,” Proceedings of the Institue of Mechanical Engineering, Vol. 168, No. 1, 1954, pp. 191-200. doi:10.1243/PIME_PROC_1954_168_023_02
- J. M. Alexander, “A Slip Line Field for Hot Rolling Process,” Proceedings of the Institute of Mechanical Engineering, Vol. 169, No. 1, 1955, pp. 1021-1030. doi:10.1243/PIME_PROC_1955_169_103_02
- T. C. Firbank and P. R. Lancaster, “A Suggested Slip-Line Field for Cold Rolling with Slipping Friction,” International Journal of Mechanics of Science, Vol. 7, No. 12, 1965, pp. 847-852.
- T. C. Firbank and P. R. Lancaster, “A Suggested Slip-Line Field for Lubricated Cold Rolling,” International Journal of Mechanics of Science, Vol. 9, No. 2, 1967, pp. 65-67. doi:10.1016/0020-7403(67)90044-6
- I. F. Collins, “Slip Line Field Solutions for Compression and Rolling with Slipping Friction,” International Journal of Mechanics of Science, Vol. 11, No. 12, 1969, pp. 971-978. doi:10.1016/0020-7403(69)90009-5
- P. Dewhurst and I. F. Collins, “A Matrix Technique for Constructing Slip-Line Field Solutions to a Class of Plane Strain Plasticity Problems,” International Journal for Numerical Methods in Engineering, Vol. 7, No. 3, 1973, pp. 357-378. doi:10.1002/nme.1620070312
- M. Salimi and M. Kadkhodaei, “Slab Analysis of Asymmetrical Sheet Rolling,” Journal of Materials Processing Technology, Vol. 150, No. 3, 2004, pp. 215-222. doi:10.1016/j.jmatprotec.2004.01.011
- R. Hill, “The Mathematical Theory of Plasticity,” 1st Edition, Oxford University Press, Oxford, 1950.
- B. Avitzur, “Metal Forming: The Application of Limit Analysis,” Marcel Dekker, Inc., New York, 1980.
- N. R. Chitkara and M. A. Butt, “Combined Rod and Tube Extrusion: Numerical Solution of Axi-Symmetric SlipLine Fields and Associated Velocity Fields,” International Journal of Mechanical Sciences, Vol. 39, No. 4, 1997, pp. 435-454. doi:10.1016/S0020-7403(96)00038-0
- N. Fang and P. Dewhurst, “Slip-Line Modeling of Built-Up Edge Formation in Machining,” International Journal of Mechanical Sciences, Vol. 47, No. 7, 2005, pp. 1079- 1098. doi:10.1016/j.ijmecsci.2005.02.008
- W. S. Weroński, A. Gontarz and Z. B. Pater, “Analysis of the Drop Forging of a Piston Using Slip-Line Fields and FEM,” International Journal of Mechanical Sciences, Vol. 39, No. 2, 1997, pp. 211-213, 215-220. doi:10.1016/0020-7403(96)00055-0
- K. Mori, K. Osakada and T. Oda, “Simulation of PlaneStrain Rolling by the Rigid-Plastic Finite Element Method,” International Journal of Mechanical Sciences, Vol. 24, No. 9, 1982, pp. 519-527. doi:10.1016/0020-7403(82)90044-3
- J. Synka and A. Kainz, “A Novel Mixed Eulerian-Lagrangian Finite-Element Method for Steady-State Hot Rolling Processes,” International Journal of Mechanical Sciences, Vol. 45, No. 12, 2003, pp. 2043-2060. doi:10.1016/j.ijmecsci.2003.12.008
- J. Chakrabaty, “Theory of Plasticity,” 3rd Edition, Elsevier, Butterworth-Heinemann, Oxford, 2006.
- M. Konyaeva, “Fundamentals of the Theory of Plasticity,” 1st Edition, Mir Publishers, Moscow, 1974.

