Engineering
Vol. 3 No. 3 (2011) , Article ID: 4151 , 4 pages DOI:10.4236/eng.2011.33033
MHD Flow, and Heat Transfer with Effects of Buoyancy, Viscous and Joules Dissipation over a Nonlinear Vertical Stretching Porous Sheet with Partial Slip
1Department of Mathematics, Gulbarga University, Gulbarga, India
2Department of Mathematics, P A College of Engineering, Mangalore, India
3Department of Mathematics, Rajiv Gandhi Institute of Technology, Bangalore, India
E-mail: msabel2001@yahoo.co.uk
Received October 8, 2010; revised November 29, 2010; accepted December 29, 2010
Keywords: MHD, Nonlinear Stretching Parameter, Joules Dissipation, Viscous Dissipation, Eckert Number, Slip Parameter
ABSTRACT
In this paper, the problem of steady laminar two-dimensional boundary layer MHD flow and heat transfer of an incompressible viscous fluid with the presence of buoyancy force and viscous dissipation over an vertical nonlinear stretching sheet with partial slip is investigated numerically. Numerical solutions of the resulting nonlinear boundary value problem in the case when the sheet stretches with a velocity varying nonlinearly with the distance is carried out. The effects of for various values of suction parameter, magnetic parameter, Prandtl number, Eckert number, buoyancy parameter, nonlinear stretching parameter and slip parameter on flow and heat transfer characteristics is investigated.
1. Introduction
The study of flow over a stretching sheet has generated much interest in recent years in view of its numerous industrial applications such as the aerodynamic extrusion of plastic sheets, the boundary layer along a liquid film, condensation process of metallic plate in a cooling bath and glass, and also in polymer industries. Since the pioneering work of Sakiadis [1] which studied the moving plate flow problem, wherein various aspects of the problem have been investigated by many authors such as Cortell [2], Xu and Liao [3], Hayat et al. [4] etc.
The study of two-dimensional boundary layer flow, heat and mass transfer over a porous stretching surface is very important as it finds many practical applications in different areas. To be more specific, it may be pointed out that many metallurgical processes involve the cooling of continuous strips or filaments by drawing them through a quiescent fluid and that in the process of drawing these strips, are sometimes stretched. Viscous dissipation changes the temperature distributions by playing a role like an energy source,which leads to affect heat transfer rates. The merit of the effect of viscous dissipation depends on whether the sheet is being cooled or heated.
Apart from the viscous dissipation, the Joules dissipation also acts as a volumetric heat source. Heat transfer analysis over porous surface is of much practical interest due to its abundant applications. To be more specific, heat-treated materials travelling between a feed roll and wind-uproll or materials manufactured by extrusion, glass-fiber and paper production, cooling of metallic sheets or electronic chips, crystal growing are a few practical applications of flow over a stretching sheet. In all these cases, the final product of desired characteristics depends on the rate of cooling and also the rate of of stretching. In view of all these aspects, the present work deals with the effect of viscous and Joules dissipation on MHD flow, heat and mass transfer over a porous sheet, with partial slip. Researches in these fields have been conducted by many investigators. For example, analytical results were carried out by Vajravelu and Hadjinicolaou [5] who took into account the effects of viscous dissipation and internal heat generation. An analysis of thermal boundary layer in an electrically conducting fluid over a linearly stretching sheet in the presence of a constant transverse magnetic field with suction or blowing at the sheet was carried out by Chaim [6].
Very recently, the viscous and joules dissipation and internal heat generation was taken into account in the energy equation. Sajid et al. [7] investigated the nonsimilar analytic solution for MHD flow and heat transfer in a third-order fluid over a stretching sheet. He found that the skin friction coefficient decreases as the magnetic parameter or the third grade parameter increases. A mathematical analysis has been carried out on momentum and heat transfer characteristics in an incompressible, electrically conducting viscoelastic boundary layer fluid flow over a linear stretching sheet by Abel et al. [8].
A numerical reinvestigation of MHD boundary layer flow over a heated stretching sheet with variable viscosity has been analyzed by Pantokratoras [9].
Ishak et al. [10] studied mixed convection boundary layers in the stagnation-point flow of an incompressible viscous fluid over a stretching vertical sheet.
Hossain and Takhar [11] have investigated the radiation effect on mixed convection boundary layer flow of an optically dense viscous incompressible fluid along a vertical plate with uniform surface temperature.
The problem of non-linear stretching sheet for different cases of fluid flow has also been analyzed by different researchers. Vajravelu [12] examined fluid flow over a nonlinearly stretching sheet. Cortell [13] has worked on viscous flow and heat transfer over a non-linearly stretching sheet. Cortell [14] further investigated on the effects of viscous dissipation and radiation on the thermal boundary layer, over a non-linearly stretching sheet. Raptis et al. [15] studied viscous flow over a non-linear stretching sheet in the presence of a chemical reaction and magnetic field. Abbas and Hayat [16] addressed the radiation effects on MHD flow due to a stretching sheet in porous space. Cortell [17] investigated the influence of similarity solution for flow and heat transfer of a quiescent fluid over a non-linear stretching surface. Awang and Kechil [18] obtained the series solution for flow over nonlinearly stretching sheet with chemical reaction and magnetic field. Cortell [19] investigated the influence of similarity solution for flow and heat transfer of a quiescent fluid over a non-linear stretching surface.
The study of magnetohydrodynamics of a conducting fluid finds applications in a variety of astroph-ysical and geophysical problems. The effects of magnetic field on the natural convection heat transfer have been discussed by Romig [20], Elbashbeshy [21], considered heat transfer over a stretching surface with a variable surface heat flux. The convective heat transfer in an electrically conducting fluid at a stretching surface has been studied by Vajravelu and Hadjinicolaou [22]. Other studies dealing with hydromagnetic flows can be found in Grandet et al. [23] Takhar and Ram [24], and Duwairi and Damseh [25].
Hence the present study investigates the effect of viscous and Joules dissipation on MHD flow over a porous nonlinear vertical stretching sheet with viscous and joules dissipation with partial slip.
2. Mathematical Analysis
Two-dimensional, nonlinear, steady, MHD laminar boundary layer flow with heat transfer of a viscous, incompressible and electrically conducting fluid over a porous vertical stretching sheet embedded in the presence of transverse magnetic field including viscous and Joules dissipation is considered for investigation. An uniform transverse magnetic field of strength B is applied parallel to y-axis. Consider a stretching sheet that emerges out of a slit at x = 0, y = 0 and subsequently being stretched, as in a polymer extrusion process. Let us assume that the speed at a point on the plate is proportional to the power of its distance from the slit and the boundary layer approximations are applicable. In writing the following equations, it is assumed that the induced magnetic field, the external electric field and the electric field due to the polarization of charges are negligible.
Consider a steady, two-dimensional free convection flow adjacent to a nonlinear stretching vertical sheet immersed in an incompressible electrically conducting viscous fluid of temperature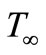 . The stretching velocity
. The stretching velocity  and the surface temperature
and the surface temperature 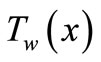 are where a and b are constants with
are where a and b are constants with  and
and .
.
The sheet is assumed to vary nonlinearly with the distance x from the leading edge, i.e.  and
and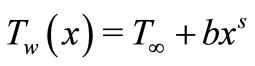 . Under these conditions, the governing boundary layer equations of momentum, energy with buoyancy, viscous and Joules dissipation, with partial slip are
. Under these conditions, the governing boundary layer equations of momentum, energy with buoyancy, viscous and Joules dissipation, with partial slip are
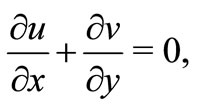 (1)
(1)
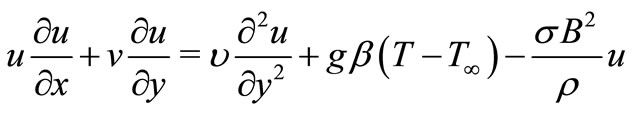 (2)
(2)
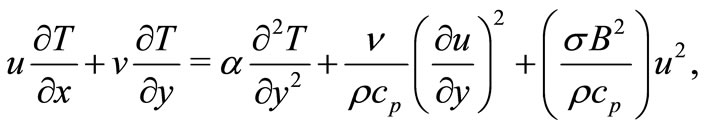 (3)
(3)
and are subjected to the following boundary conditions
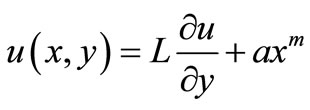 ,
,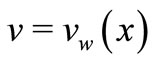 ,
,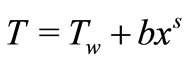 at
at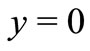 where
where 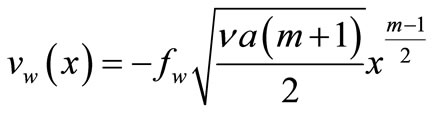
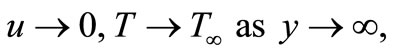 (4)
(4)
where u and v are the velocity components along the x and y axes, respectively. Further, μ, ρ, α, β, T, and g are the dynamic viscosity, fluid density, thermal diffusivity, thermal expansion coefficient, fluid temperature in the boundary layer, and acceleration due to gravity, respectively.
A common feature of all these analyses is the assumption that the flow field obeys the conventional no-slip condition at the sheet that is the velocity component  parallel with the sheet becomes equal to the sheet velocity
parallel with the sheet becomes equal to the sheet velocity 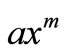 at the sheet. In certain situations, however, the assumption of no-slip does no longer apply and should be replaced by a partial slip boundary condition which relates the fluid velocity u to the shear rate
at the sheet. In certain situations, however, the assumption of no-slip does no longer apply and should be replaced by a partial slip boundary condition which relates the fluid velocity u to the shear rate  at the boundary. Here L is the slip length, and y denotes the coordinate perpendicular to the surface. This slip-flow condition was first introduced by C-L. M. H. Navier more than a century ago and has more recently been used in studies of fluid flow past permeable walls, slotted plates, rough and coated surfaces, and gas and liquid flow in micro devices. The no-slip boundary condition is known as the central tenets of the Navier-Stokes theory. But there are situations wherein such condition is not appropriate. Especially, no slip condition is inadequate for most non-Newtonian fluids. For example polymer melts often exhibit macroscopic wall slip and that in general is governed by a non-linear and monotone relation between the slip velocity and traction. The fluids exhibiting boundary slip find applications in technology such as in the polishing of artificial heart valves and internal cavities. Navier suggested a slip boundary condition in terms of linear shear stress.
at the boundary. Here L is the slip length, and y denotes the coordinate perpendicular to the surface. This slip-flow condition was first introduced by C-L. M. H. Navier more than a century ago and has more recently been used in studies of fluid flow past permeable walls, slotted plates, rough and coated surfaces, and gas and liquid flow in micro devices. The no-slip boundary condition is known as the central tenets of the Navier-Stokes theory. But there are situations wherein such condition is not appropriate. Especially, no slip condition is inadequate for most non-Newtonian fluids. For example polymer melts often exhibit macroscopic wall slip and that in general is governed by a non-linear and monotone relation between the slip velocity and traction. The fluids exhibiting boundary slip find applications in technology such as in the polishing of artificial heart valves and internal cavities. Navier suggested a slip boundary condition in terms of linear shear stress.
The momentum, and energy Equations (2), (3), and (4) can be transformed into the corresponding nonlinear ordinary differential equations by the following similarity transformation:


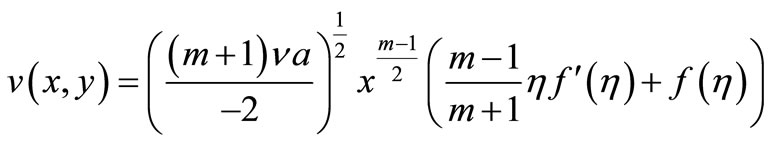 (5)
(5)
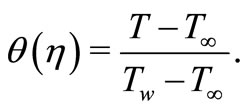 (6)
(6)
where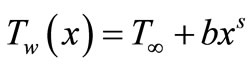 , b is dimensional constant and s is the index of power law variation of temperature.
, b is dimensional constant and s is the index of power law variation of temperature.
The transformed nonlinear ordinary differential equations are
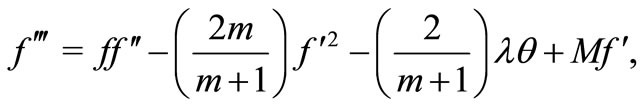 (7)
(7)
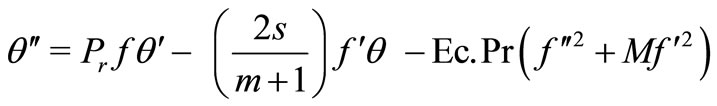 (8)
(8)
Boundary conditions (4) becomes
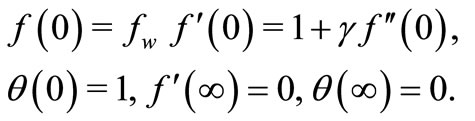 (9)
(9)
where![]() ,
,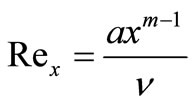 ,
,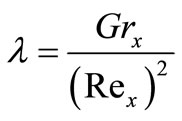 , and
, and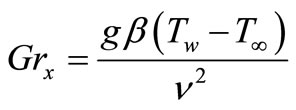 .
.
3. Numerical Solution
The nonlinear boundary value problem represented by Equations (7) to (9) is solved numerically using Fourthorder Runge Kutta shooting technique.
The system of non-linear ordinary differential Equations (7) and (8) together with the boundary conditions Equation (9) are similar and are solved numerically by using the fourth order of Runge Kutta integration scheme accompanied with the Shooting scheme. Making an initial guess for the values of 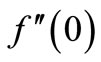 and
and 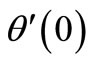 to initiate the shooting process is very crucial in this process. The success of the procedure depends very much on how good this guess is. Numerical solutions are obtained for several values of the physical parameters i.e. magnetic parameter M, stretching parameter m, Prandtl number Pr, slip parameter
to initiate the shooting process is very crucial in this process. The success of the procedure depends very much on how good this guess is. Numerical solutions are obtained for several values of the physical parameters i.e. magnetic parameter M, stretching parameter m, Prandtl number Pr, slip parameter  Buoyancy parameter
Buoyancy parameter![]() , Eckert number (Ec) and, suction/injection parameter
, Eckert number (Ec) and, suction/injection parameter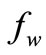 .
.
We have chosen a step size of 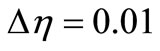 to satisfy the convergence criterion of 10–6 in all cases. The maximum value of
to satisfy the convergence criterion of 10–6 in all cases. The maximum value of 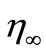 was found to each iteration loop by
was found to each iteration loop by  The maximum value of
The maximum value of  to each group of parameter is determined when the value of the unknown boundary conditions at
to each group of parameter is determined when the value of the unknown boundary conditions at  is not changed to successful loop with error less than 10–6.
is not changed to successful loop with error less than 10–6.
4. Results and Discussion
In order to gain physical insight, the velocity, and temperature profiles have been discussed by assigning numerical values to the parameter, encountered in the problem i.e. numerical calculations were carried out for different values of suction parameter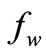 , magnetic parameter M, power law stretching parameter m, Prandtl number Pr, Eckert number Ec, buoyancy parameter λ, slip parameter γ, and their effects on flow and heat transfer characteristics are analysed graphically.
, magnetic parameter M, power law stretching parameter m, Prandtl number Pr, Eckert number Ec, buoyancy parameter λ, slip parameter γ, and their effects on flow and heat transfer characteristics are analysed graphically.
The influences of the magnetic parameter M on the longitudinal velocity profile is depicted in Figure 1. It can be seen that increasing M is to reduce the velocity distribution in the boundary layer which results in thinning of the boundary layer thickness, and hence induces an increase in the absolute value of the velocity gradient at the surface.
The influence of suction parameter  (
( < 0), over the non-dimensional longitudinal velocity profiles are shown in Figure 2. It is seen that the effect of suction parameter decelerates the longitudinal velocity.
< 0), over the non-dimensional longitudinal velocity profiles are shown in Figure 2. It is seen that the effect of suction parameter decelerates the longitudinal velocity.
The influence of injection parameter 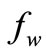 (
(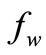 > 0), over the dimensionless longitudinal velocity profile is shown in Figure 3 and it is noticed that longitudinal velocity increases with injection. It should be noted that in Figure 2, the boundary-layer assumptions do not permit a solution of the boundary-layer equation for large
> 0), over the dimensionless longitudinal velocity profile is shown in Figure 3 and it is noticed that longitudinal velocity increases with injection. It should be noted that in Figure 2, the boundary-layer assumptions do not permit a solution of the boundary-layer equation for large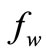 , because it will approach a constant value of 1, and the boundary layer is almost literally blown off the surface, similar to that of stationary plate with injection (Burmeister [26]; Kays and Crawford [27]).
, because it will approach a constant value of 1, and the boundary layer is almost literally blown off the surface, similar to that of stationary plate with injection (Burmeister [26]; Kays and Crawford [27]).
Figure 3 shows the effect of suction/injection on dimensionless temperature profile and it is observed that there is decrease in temperature in the thermal boundary layer resulting in thinning of thermal boundary layer thickness in the case of suction and the reverse trend is observed for injection. Further it is clear that suction (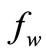 < 0) enhances the heat transfer coefficient much better than injection (
< 0) enhances the heat transfer coefficient much better than injection (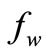 > 0), and the thickness of the thermal boundary layer is reduced. Thus, suction can be used as a means for cooling the surface much faster than injection.
> 0), and the thickness of the thermal boundary layer is reduced. Thus, suction can be used as a means for cooling the surface much faster than injection.
Figures 4 and 5, describe respectively the behaviors of the longitudinal velocity profile and temperature profile for different values of power law stretching parameter m and it is noticed that increase in m results in decrease of longitudinal velocity profile which is more pronounced for small values of m, where as temperature profile increases with the increase of stretching parameter m. It is observed that the variation of the sheet temperature has a substantial effect on the thermal boundary layer. This effect is more pronounced when sheet temperature varies in the direction of highest stretching rate.
An increase in Prandtl number Pr is associated with a decrease in the temperature distribution which is displayed in Figure 6, which is consistent with the fact that thermal boundary layer thickness decreases with increase in the values of Prandtl number. The rate of heat transfer increases with the increasing values of Prandtl number. The boundary layer edge is reached faster as Pr increases.
Dimensionless velocity profile  is presented in Figure 7 for some different values of the slip parameter γ. It is readily seen that γ has a substantial effect on the
is presented in Figure 7 for some different values of the slip parameter γ. It is readily seen that γ has a substantial effect on the
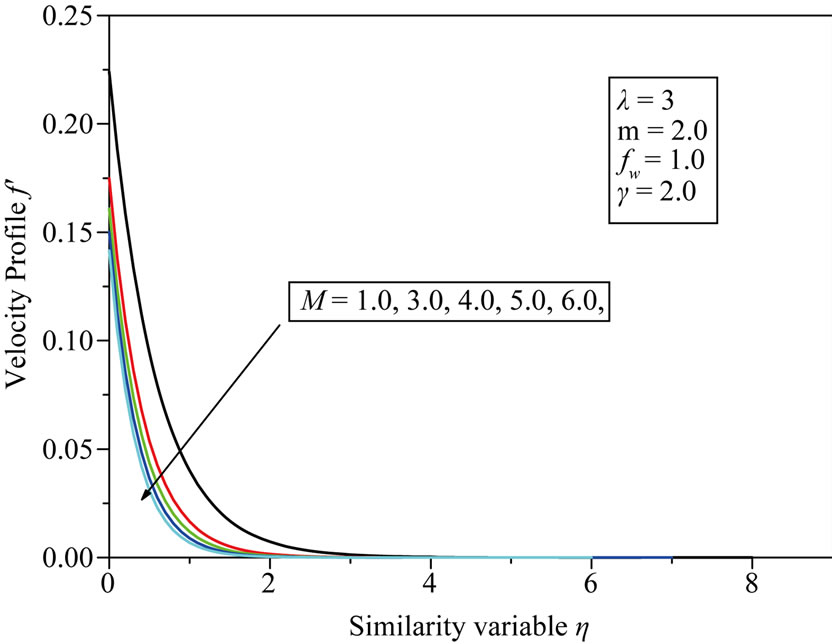
Figure 1. Velocity profile f' versus similarity variable η for different values of magnetic parameter.

Figure 2. Dimensionless velocity profile f' versus similarity variable η for different values of suction/injection parameter.

Figure 3. Temperature profile θ(η) vs similarity variable η for different values of suction/injection.
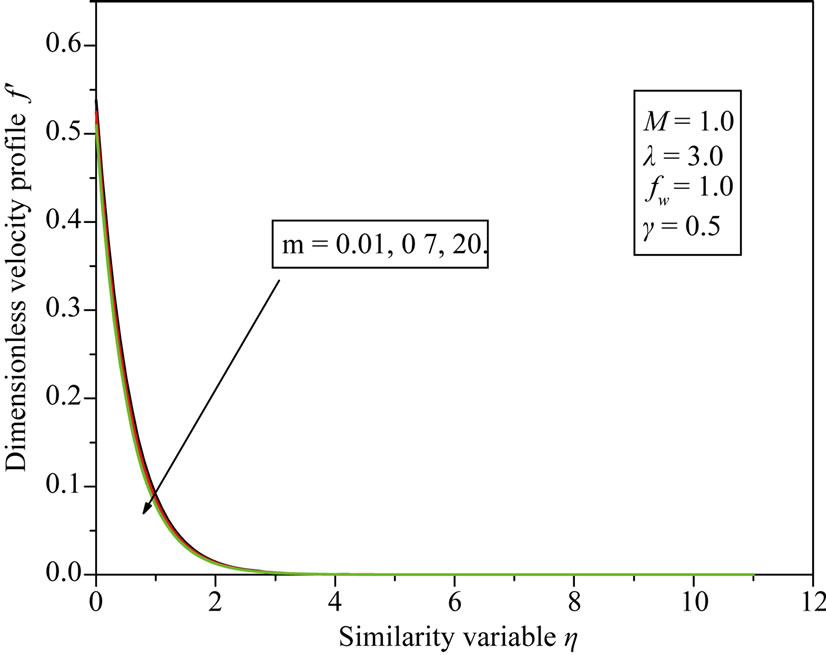
Figure 4. Dimensionless velocity profile f' vs similarity variable η for different values of m.

Figure 5. Dimensionless temperature profile θ(η) vs similarity variable η for different values of m.

Figure 6. Temperature profile θ(η) versus similarity variable η for different values of Pr.
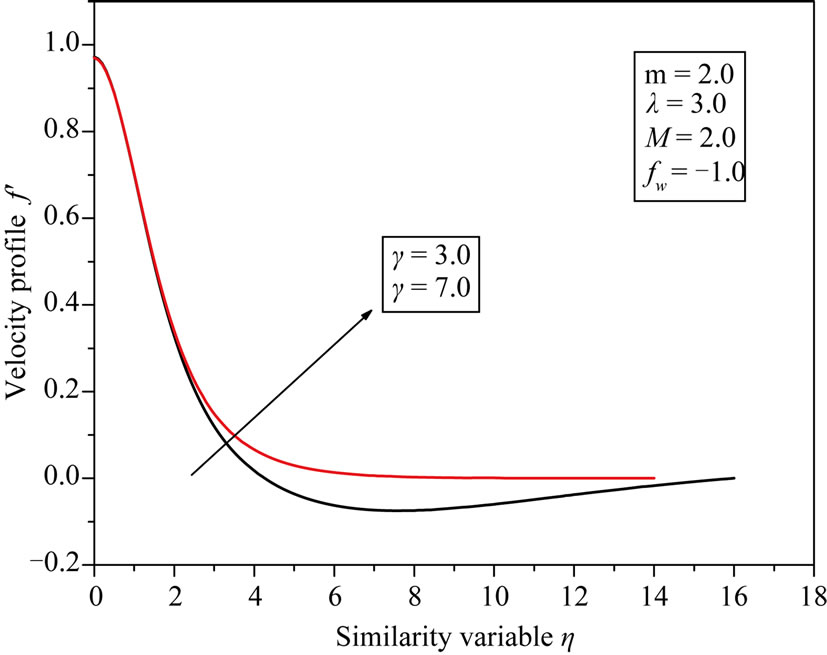
Figure 7. Dimensionless velocity profile f' versus similarity variable η for different values of slip parameter γ.

Figure 8. Dimensionless velocity profile vs similarity variable η for different values of buoyancy parameter λ.

Figure 9. temperature profile θ(η) versus similarity variable η for different values of Ec.
solutions. In fact, the amount of slip  increases monotonically with γ from the no-slip solution for
increases monotonically with γ from the no-slip solution for 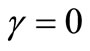 and towards full slip as γ tends to infinity. The latter limiting case implies that the frictional resistance between the viscous fluid and the surface is eliminated, and the stretching of the sheet does no longer impose any motion of the fluid.
and towards full slip as γ tends to infinity. The latter limiting case implies that the frictional resistance between the viscous fluid and the surface is eliminated, and the stretching of the sheet does no longer impose any motion of the fluid.
In Figure 8, the effects of buoyancy parameter λ on dimensionless longitudinal velocity is shown graphically and the effects of buoyancy force is found to be more pronounced for a fluid with a small Pr. Thus, fluid with smaller Pr is more susceptible to buoyancy force effects.
The influence of Eckert number Ec over dimensionless temperature profiles are shown in Figure 9. We observed from Figure 9, that an increase in Eckert number Ec enhances the temperature because the heat energy is stored in the liquid due to the frictional heating.
The velocity and temperature profiles presented in Figures 1-9, show that the far field boundary conditions are satisfied asymptotically, which support the validity of the numerical results presented.
5. REFERENCES
- B. C. Sakiadis, “Boundary-Layer Behavior on Continuous Solid Surfaces: I Boundary Layer Equations for Two Dimensional and Axisymmetric Flow,” AIChE Journal, Vol. 7, No. 1, 1961, pp. 26-28. doi:10.1002/aic.690070108
- R. Cortell, “Effects of Viscous Dissipation and Work Done by Deformation on the MHD Flow and Heat Transfer of a Viscoelastic Fluid over a Stretching Sheet,” Physics Letters A, Vol. 357, No. 4-5, 2006, pp. 298-305. doi:10.1016/j.physleta.2006.04.051
- H. Xu and S. J. Liao, “Series Solutions of Unsteady Magnetohydrodynamics Flows of Non-Newtonian Fluids Caused by an Impulsively Stretching Plate,” Journal of Non-Newtonian Fluid Mechanics, Vol. 159, 2005, pp. 46-55. doi:10.1016/j.jnnfm.2005.05.005
- M. Sajid and T. Hayat, “Influence of Thermal Radiation on the Boundary Layer Flow due to an Exponentially Stretching Sheet,” International Communications in Heat and Mass Transfer, Vol. 35, No. 3, 2008, pp. 347-356. doi:10.1016/j.icheatmasstransfer.2007.08.006
- K. Vajravelu and A. Hadjinicolaou, “Heat Transfer in a Viscous Fluid over a Stretching Sheet with Viscous Dissipation and Internal Heat Generation,” International Communications in Heat and Mass Transfer, Vol. 20, No. 3, 1993, pp. 417-430. doi:10.1016/0735-1933(93)90026-R
- T. C. Chaim, “Magnetohydrodynamic Heat Transfer over a Non-Isothermal Stretching Sheet,” Acta Mechanica, Vol. 122, No. 1-4, 1977, pp. 169-179. doi:10.1007/BF01181997
- M. Sajid, T. Hayat and S. Asghar, “Non-Similar Analytic Solution for MHD Flow and Heat Transfer in a ThirdOrder Fluid over a Stretching Sheet,” International Journal of Heat and Mass Transfer, Vol. 50, No. 9-10, 2007, pp. 1723-1736. doi:10.1016/j.ijheatmasstransfer.2006.10.011
- M. S. Abel, E. Sanjayanand and M. M. Nandeppanavar, “Viscoelastic MHD Flow and Heat Transfer over a Stretching Sheet with Viscous and Ohmic Dissipations,” Communications in Nonlinear Science and Numerical Simulation, Vol. 13, No. 9, 2008, pp. 1808-1821. doi:10.1016/j.cnsns.2007.04.007
- A. Pantokratoras, “Study of MHD Boundary Layer Flow over a Heated Stretching Sheet with Variable Viscosity: A Numerical Reinvestigation,” International Journal of Heat and Mass Transfer, Vol. 51, No. 1-2, 2008, pp. 104- 110. doi:10.1016/j.ijheatmasstransfer.2007.04.007
- A. Ishak, R. Nazar and I. Pop, “Mixed Convection Boundary Layer in the Stagnation Point Flow towards Stretching Vertical Sheet,” Meccanica, Vol. 41, No. 5, 2006, pp. 509-518. doi:10.1007/s11012-006-0009-4
- M. A. Hossain and H. S. Takhar, “Radiation Effect on Mixed Convection along a Vertical Plate with Uniform Surface Temperature,” Heat Mass Transfer, Vol. 31, No. 4, 1996, pp. 243-248. doi:10.1007/BF02328616
- K. Vajravelu, “Fluid Flow over a Nonlinearly Stretching Sheet,” Applied Mathematics and Computation, Vol. 181, No. 1, 2006, pp. 609-618. doi:10.1016/j.amc.2005.08.051
- R. Cortell, “MHD Flow and Heat Transfer of an Electrically Conducting Fluid of Second Grade in a Porous Medium over a Stretching Sheet Subject with Chemically Reactive Species,” Chemical Engineering and Processing, Vol. 46, No. 8, 2007, pp. 721-728. doi:10.1016/j.cep.2006.09.008
- R. Cortell, “Viscous Flow and Heat Transfer over a NonLinearly Stretching Sheet,” Applied Mathematics and Computation, Vol. 184, No. 2, 2007, pp. 864-873. doi:10.1016/j.amc.2006.06.077
- A. Raptis and C. Perdikis, “Viscous Flow over a NonLinearly Stretching Sheet in the Presence of a Chemical Reaction and Magnetic Field,” International Journal of Non-Linear Mechanics, Vol. 41, No. 4, 2006, pp. 527- 529. doi:10.1016/j.ijnonlinmec.2005.12.003
- Z. Abbas and T. Hayat, “Radiation Effects on MHD Flow in a Porous Space,” International Journal of Heat and Mass Transfer, Vol. 51, No. 5-6, 2008, pp. 1024-1033. doi:10.1016/j.ijheatmasstransfer.2007.05.031
- R. Cortell, “Effects of Viscous Dissipation and Radiation on the Thermal Boundary Layer over a Non-Linearly Stretching Sheet,” Physics Letters A, Vol. 372, No. 5, 2008, pp. 631-336. doi:10.1016/j.physleta.2007.08.005
- S. A. Kechil and I. Hashim, “Series Solution of Flow over Nonlinearly Stretching Sheet with Chemical Reaction and Magnetic Field,” Physics Letters A, Vol. 372, No. 13, 2008, pp. 2258-2263. doi:10.1016/j.physleta.2007.11.027
- R. Cortell, “Similarity Solution for Flow and Heat Transfer of a Quiescent Fluid over a Non-Linearly Stretching Surface,” Journal of Materials Processing Technology, Vol. 203, No. 1-3, 2008, pp. 176-183. doi:10.1016/j.jmatprotec.2007.09.055
- M. Romig, “The Influence of Electric and Magnetic Field on Heat Transfer to Electrically Conducting Fluids,” Advances in Heat Transfer, Vol. 1, 1964, pp. 267-354. doi:10.1016/S0065-2717(08)70100-X
- E. M. A. Elbashbeshy, “Heat Transfer over a Stretching Surface with Variable Surface Heat Flux,” Journal of Physics D: Applied Physics, Vol. 31, No. 16, 1998, pp. 1951-1955. doi:10.1088/0022-3727/31/16/002
- K. Vajravelu and A. Hadjinicolaou, “Convective Heat Transfer in an Electrically Conducting Fluid at a Stretching Surface with Uniform Free Stream,” International Journal of Engineering Science, Vol. 35, No. 12-13, 1997, pp. 1237-1244. doi:10.1016/S0020-7225(97)00031-1
- J. P. Grandet, T. Alboussiere and R. Moreau, “Buoyancy Driven Convection in a Rectangular Enclosure with a Transverse Magnetic Field,” International Journal of Heat and Mass Transfer, Vol. 35, No. 4, 1992, pp. 741-748. doi:10.1016/0017-9310(92)90242-K
- H. S. Takhar and P. C. Ram, “Magnetohydrodynamic Free Convection Flow of Water at 4 Degree Centigrade, through a Porous Medium,” International Communications in Heat and Mass Transfer, Vol. 21, No. 3, 1994, pp. 371-376. doi:10.1016/0735-1933(94)90005-1
- H. M. Duwairi and R. A. Damseh, “Magnetohydrodynamic Natural Convection Heat Transfer from Radiate Vertical Porous Surfaces,” Heat Mass Transfer, Vol. 40, No. 10, 2004, pp. 787-792. doi:10.1007/s00231-003-0476-2
- L. C. Burmeister, “Convective Heat Transfer,” Wiley, New York, 1983.
- W. M. Kays and M. E. Crawford, “Convective Heat and Mass Transfer,” 2nd Edition, McGraw-Hill, New York, 1987.
Nomenclature
u, v: velocity component along the x, y directions
g: acceleration due to gravity
T: temperature of the fluid inside the thermal boundary layer
Tw: Wall temperaturetemperature
T∞: Temperature of the fluid at infinity
cp: specific heat at constant pressure
vw: velocity of suction
Pr: Prandtl number
 : Local Grashof Number
: Local Grashof Number
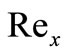 : Local Reynolds Number
: Local Reynolds Number
λ: buoyancy parameter
f: dimensionless stream function
m: nonlinear stretching parameter
fw: dimensionless suction/injection parameter
υ: kinematic viscosity
g: Slip Parameter
s : Index of power law variation of temperature.
r: density of the fluid
b: coefficient of volume expansion
![]() : Thermal diffusivity
: Thermal diffusivity
k: thermal conductivity
η: similarity variable
θ: dimensionless temperature

