Engineering
Vol. 3 No. 2 (2011) , Article ID: 4291 , 4 pages DOI:10.4236/eng.2011.32022
Modulation Index Effect on the 5-Level SHE-PWM Voltage Source Inverter
Islamic Azad University, Ashtian Branch, Ashtian, Iran
Email: hfeshki@yahoo.com
Received October 21, 2010; revised November 19, 2010; revised November 29, 2010
Keywords: Multilevel Voltage Source Inverter, Selective Harmonic Elimination, Modulation Index, Load Type and PSPICE
ABSTRACT
Harmonic content of the voltage source inverters is important and must be in the allowed ranges. Different method are proposed to decrease the Total Harmonic Distortion (THD) and caused to be sinusoidal the output voltage of inverters. One of these methods is using multilevel structure. In this structure many important parameters which are effective on voltage source inverter operation that among them we can mention to modulation index (MI). Variation of modulation index can change the THD. One of the harmonic reduction methods is using multilevel structure. In this paper, a sample 5-level SHE-PWM voltage source inverter is presented and all equation and choosing switching angles for elimination desired harmonics from different order. To investigate the effective parameters on the inverter operation, a typical 5-level inverter is simulated in PSPICE software. The simulation has been done for different values of modulation and its effect on the inverter operation is evaluated.
1. Introduction
Voltage source inverters have many applications in industry and to use them, the effective parameters on their operation should be carefully studied. One of the applications of voltage source inverters is to motor drive in which the modulation index and frequency should be change to control the amplitude and speed. Hence, the variation of these parameters should be analyzed [1-5].
Different methods have been presented for harmonic elimination or reduction from output of voltage source inverter up to now. In [6-13], the multi level structure has been used to harmonic elimination.
Many different PWM pattern strategies have been reported in the literature for VSI. These include many different on-line (e.g., sinusoidal pulse width modula-tion, SPWM) or off-line (e.g., selective harmonic elimi-nation and magnitude modulation, SHE-PWM) patterns for fundamental magnitude control and harmonic reduc-tion [14-15]. As other switching methods, we can men-tion the switching method of selective harmonic elimi-nation (SHE-PWM) is able to eliminate desired harmo-nics from different order. In this method, low order harmonics are eliminated by switching and high ones by using filter in the output [16-19]. In this paper, the effect of some parameters such as modulation index and load type on the voltage source inverter is investigated. By using a new switching method for this purpose, a sample 5-level voltage source inverter is simulated in PSPICE software and the effects of modulation index variation on inverter function are studied. Also some simulations are done for resistive-inductive load in the output of the inverter.
2. Introduction of Shem Switching Method
SHEM is a PWM switching method for harmonic elimination which harmonic of output voltage can be eliminated by creating appropriate notches [20-22]. In this method, for elimination of N harmonics, N notches must be created in quarter of the waveform and if control of amplitude is necessary, one more notch is needed for this purpose. Hence, for having both amplitude control and harmonic elimination in total N+1 notches is needed.
Using this method, lower order harmonics are cancelled by proper switching and higher order harmonics are filtered by high pass filter. Moreover, elimination of harmonics is optional and possible. In Figure 1, voltage waveform of the output phase is shown. According to the figure, the amplitude can be controlled and the harmonics number 5, 7 can be cancelled using  angles.
angles.
This switching method when compared to other methods such as PWM, SPWM and etc, has some advantages. This method can be implemented in the power system harmonic studying. This study is based on the fact that some optional harmonics can be held and the others can be removed from output. Another advantage of this method is low switching losses because of its low switching frequency.
3. Introduction of Presented Switching Method for Multi Level Inverters
In SHE-PWM, method, (one of the switching method) the place, number and the width of every notch are so effective on controlling the amplitude and eliminating different harmonics. Therefore, the multilevel inverter can have different modes which some of them are as follow:
• Mode 1: amplitude control
• Mode 2: amplitude control and 5th, 7th harmonics elimination
• Mode 3: amplitude control and 5th, 7th, 11th and 13th harmonics elimination
These modes are optional and other modes can be selected as well. In this paper, the functions of modes 1, 3 are described and mode 2 is the same.
3.1. Function Explanation and Inverter Equations in Mode 1
One of the 5-level inventor modes is amplitude control mode (Figure 2) in which in every quarter of wave a

Figure 1. The waveform of VSI output voltage without 5 and 7 harmonics and capable of controlling amplitude.

Figure 2. 5 level voltage source inverter.
notch is created so that the amplitude can be controlled. Instead of amplitude control, one of the harmonics can be selected and eliminated.
The output voltage waveform with control signals is plotted in Figure 3. By writing Fourier series for output voltage, the following equation can be obtained:
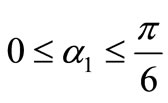
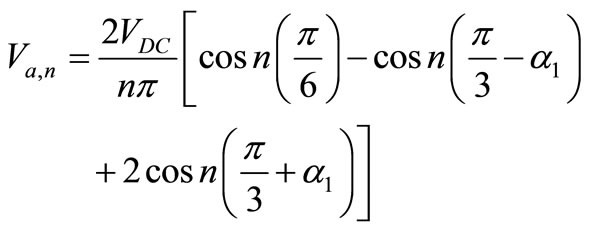 (1)
(1)
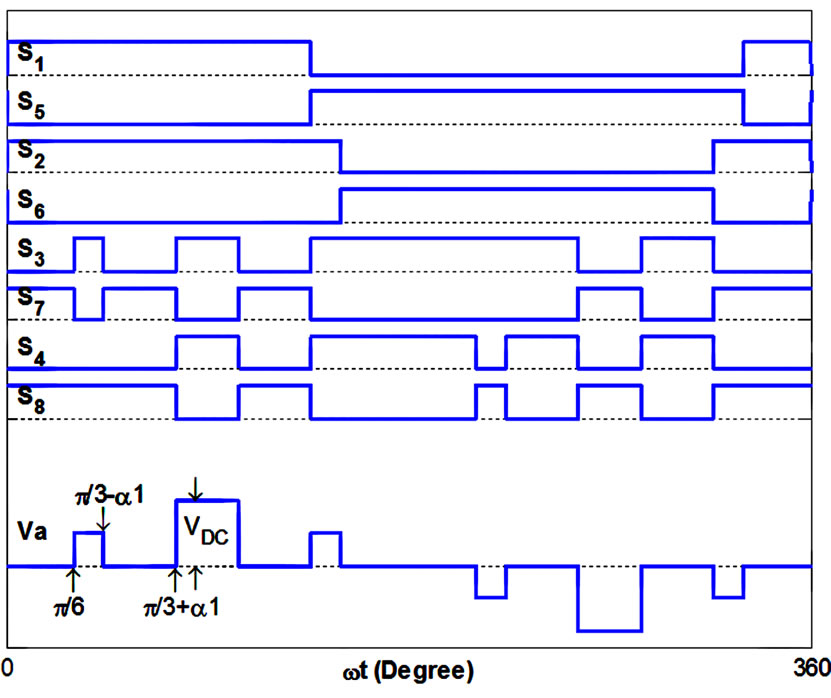
Figure 3. PWM pattern for magnitude control of output AC voltage.
Where:
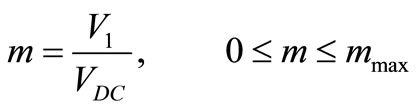 (2)
(2)
V1 is the maximum output voltage (AC), mmax is accessible extreme of modulation index.
The modulation index is maximized when the angel α1 is equal to zero. The correlation between modulation index and α1 is obtained from Equation (1) which is plotted in Figure 4. This nonlinear equation is solved by MAPLE software.
3.2. Function Explanation and Inverter Equations in Mode 2
Using SHEM method with short circuit pulses, the first two existing lower order harmonics, 5 and 7th, can be eliminated in addition to fundamental magnitude control. This is denoted as a new pattern, i.e., mode 2.
The number of required independent angles for a SHE pattern is equal to the number of variables to be controlled; hence, for this case can be suggested as shown in Figure 5. This pattern is re-drawn between 0 and π/2 Figure 6. Now the expression for the nth harmonic in Va can be written as:
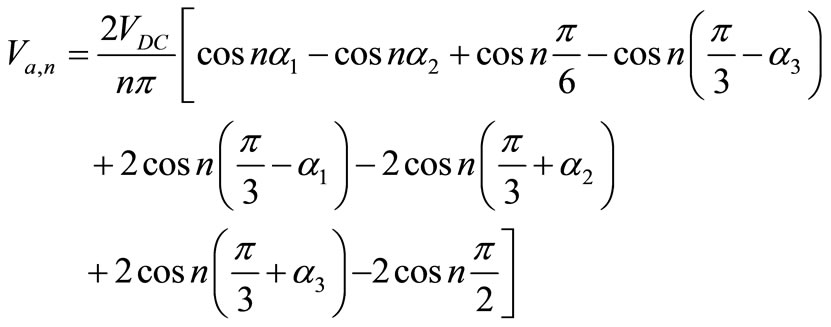 (3)
(3)
To calculate the corresponding chop angles for controlling modulation index and canceling specified harmonics in the SHE method, V1 should be set to m and Va,n to zero. The fundamental component of output voltage can be written as Equation (4).

Figure 5. PWM-SHEM pattern for 5th and 7th harmonics.
 (4)
(4)
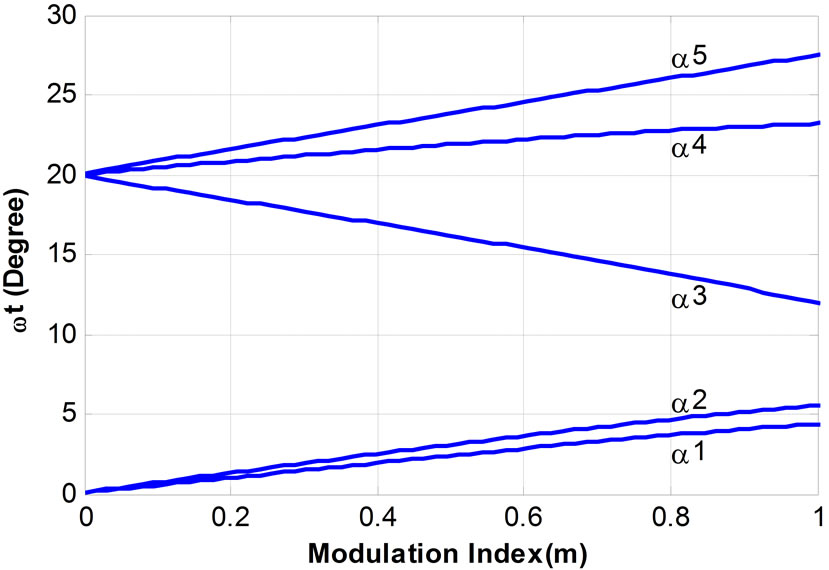
Thus, a system of nonlinear transcendental Equations (5) to (7) must be solved. The related chop angles (α1, α2 and α3) for this PWM pattern are shown versus modulation index in Figure 7.
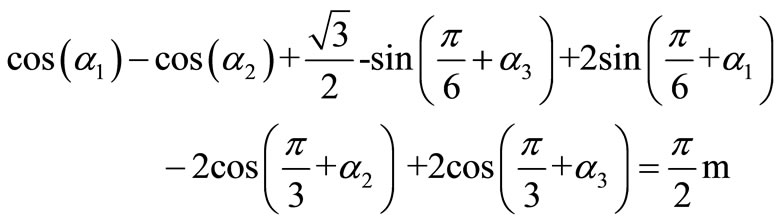 (5)
(5)
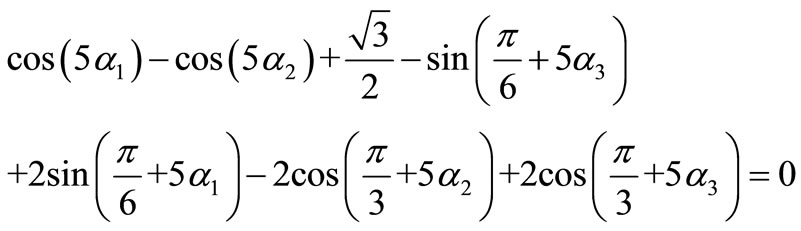 (6)
(6)
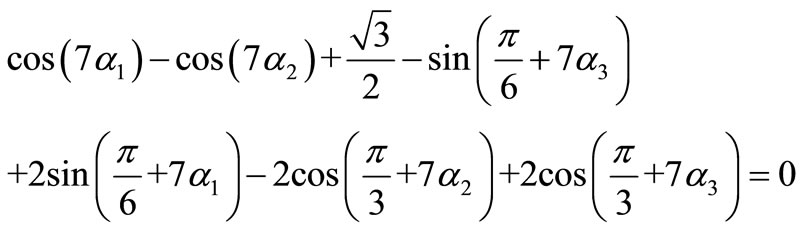 (7)
(7)
3.3. Function Explanation and Inverter Equations in Mode 3
Because the common harmonics in power systems are 6k+1 that so one of the considered modes is to eliminate 5, 7, 11 and 13th with amplitude control. In Figure 8, order signals along with the output voltage for interval 0 to 90 degree are shown. In this case, due to four harmonics elimination with amplitude control, we should create five notches in wave quarter which is clearly seen in this figure. Furrier series for the output voltage is written as (8).
so one of the considered modes is to eliminate 5, 7, 11 and 13th with amplitude control. In Figure 8, order signals along with the output voltage for interval 0 to 90 degree are shown. In this case, due to four harmonics elimination with amplitude control, we should create five notches in wave quarter which is clearly seen in this figure. Furrier series for the output voltage is written as (8).
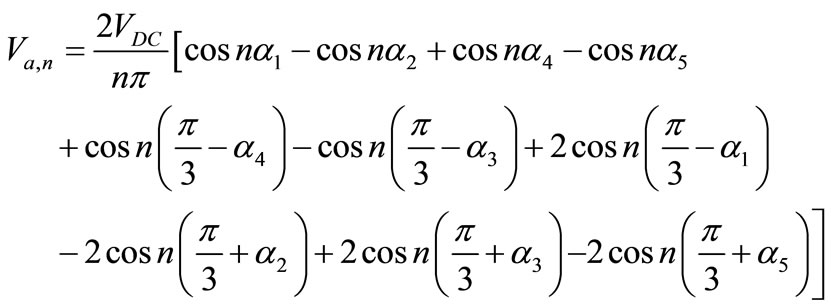 (8)
(8)
Which, the different equations can be obtained for various values of n values. Because in this mode the 5th, 7th, 11th and 13th harmonics are eliminated so the value for n should be 1, 5,7,11 and 13.in other words, there will be five equations with six variations. These equa-
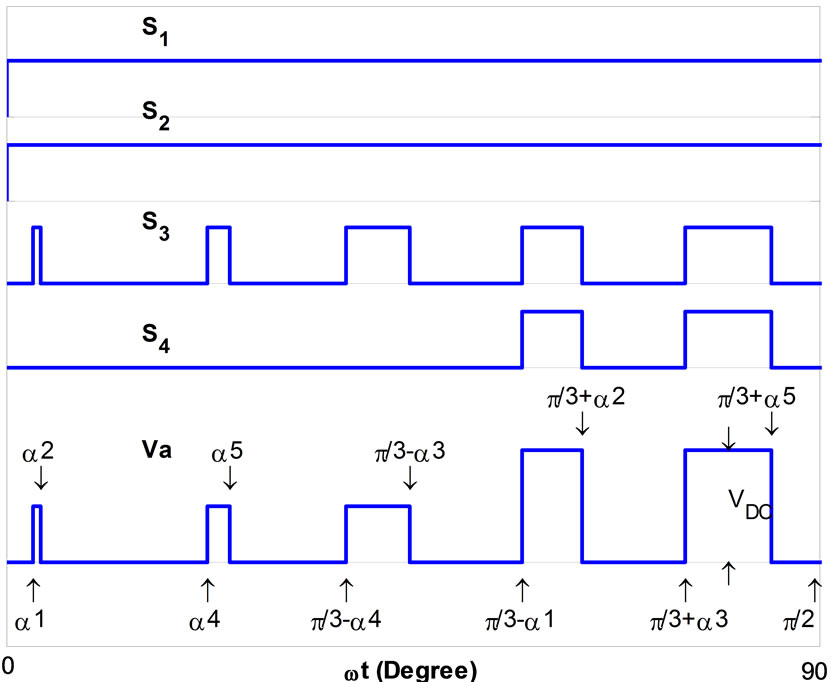
Figure 8. SHE-PWM pattern for 5, 7, 11, and 13th harmonics expansion in the 0 - π/2 region.
tions can be solved for different values of m and the values of 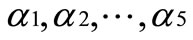 are obtained that all are plotted in Figure 9.
are obtained that all are plotted in Figure 9.
4. Simulation of 5-Level Voltage Source Inverter
The 5-level voltage source inverter in Figure 2 with the characteristic of Table 1 is stimulated. To investigate the effect of parameters on the inverter function, an inventor for 70% modulation index, the out put frequency 50Hz and resistive load is accomplished and then their effect on the function of the inverter is investigated.
4.1. Investigation of Inverter Function in Modulation Index Equal to 0.7
The out put voltage for mode 1 is shown in Figure 10.

Table 1. Parameters of simulated inverter.
According to this figure the maximum amplitude of output voltage is about 190V. In this figure the primary component amplitude can be controlled. This figure includes odd harmonics which is clear in Figure 11.
The amplitude of primary component should be about 0.7 of the output voltage amplitude. In other words, it should be approximately 133 V (190×0.7) which is equal to 130V in the figure.
In mode 3, amplitude control with 5th, 7th, 11th and 13th harmonics elimination is considered. The output voltage is shown in Figure 12. The spectrum frequency of the voltage is obvious in Figure 13. In this mode, the 5th, 7th, 11th and 13th harmonics (the frequencies of 250 Hz, 350 Hz, 550 Hz and 650 Hz) don’t exist in the output.
4.2. Modulation Index Reduction from 0.7 to 0.4
The output voltage in this mode can be seen in Figure

Figure 10. The waveform of CSI output voltage with amplitude control (MI = 0.7).

Figure 11. spectral frequency output voltage for MLCSI in mode 1 in resistive load, 50Hz output frequency and MI = 0.7.

Figure 12. The waveform of CSI output voltage without 5, 7, 11 and 13th harmonics and capable of controlling amplitude (MI = 0.7).

Figure 13. Spectral frequency output voltage for MLCSI in mode 3 in resistive load, 50Hz output frequency and MI = 0.7.
14 the maximum amplitude of this voltage is equal to190 V. In this figure, the output voltage of primary component can be controlled. This figure includes the odd harmonics which is shown in Figure 15. The primary component amplitude should be about 0.4 of the output amplitude (76V) which is equal to 72V in this figure. By comparing Figure 15 with Figure 11, it can be pointed out that the modulation index reduction leads to increase of THD. As a result, the amplitudes of existent harmonics is fundamentally increased which should be noticed.
The output voltage waveform and also its spectral

Figure 14. The waveform of CSI output voltage with amplitude control (MI = 0.4).

Figure 15. Spectral frequency output voltage for MLCSI in mode 1 in resistive load, 50Hz output frequency and MI = 0.4.
frequency in mode 3 with modulation index equal to 0.4 are plotted in Figure 16 and Figure 17 respectively. According to Figure 17, it can be found out that in spite of modulation index reduction 5, 7, 11 an 13th harmonics are eliminated well from the output. However, the modulation index reduction causes increasing of voltage THD.
According to previous section, the amplitude of the output voltage can be controlled by different methods such as variation of modulation index, changing the DC link voltage and so on. According to this paper results, the former method leads to increase the output voltage THD. So, to decrease the harmonic contents, the range of modulation index variation must be limited. There-fore in realistic situation, the THD can be controlled by either limitation of modulation index or changing the DC link voltage in constant (optimal) modulation index. But in the latter method, the cost of the system will be increased due to using additional units such as DC-DC converter to control of DC link voltage.
4.3. Load Variation from Resistive to Inductive-Resistive
In this case, a 10 mH inductor is added series to load. In

Figure 16. The waveform of CSI output voltage without 5,7,11 and 13th harmonics and capable of controlling amplitude (MI = 0.4).

Figure 17. Spectral frequency output voltage for MLCSI in mode III in resistive load, 50Hz output frequency and MI = 0.4.
the voltage source inverter, the output voltage is inde-pendent from the load and must be constant for any load. For resistive load, the output voltage and current wave for are similar and when the load is varied to inductive-resistive, the output current is not similar to output voltage. The output current for mode 1 is shown in Figure 18. The spectral frequency of the output current is shown in Figure 19. According to this figure, by adding the inductor to the load, the waveform of output current becomes sinusoidal.
The output current and its frequency spectral are shown in Figure 20 and Figure 21 respectively. The figures show the effect of load type on the output current and its spectral frequency.
5. Future Work
For the future work, the optimization of the modulation index can be studied. The effect of the modulation index is investigated in this paper and in the next work; the optimal value of these parameters can be obtained using suitable optimization method.
6. Conclusion
In this paper, the effect of different parameters such as

Figure 18. Output voltage for MLCSI in mode I in resistive-inductive load, 50Hz output frequency and MI = 0.7.
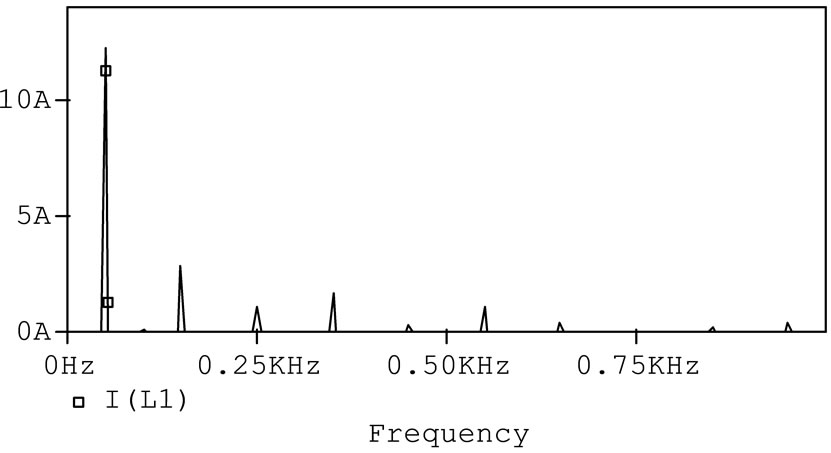
Figure 19. Spectral frequency of output voltage for MLCSI in mode 1 in inductive-resistive load, 50Hz output frequency and MI = 0.7.

Figure 20. Load output voltage in mode 1 in resistive-inductive load, 50Hz output frequency and MI = 0.7 without using capacitor.
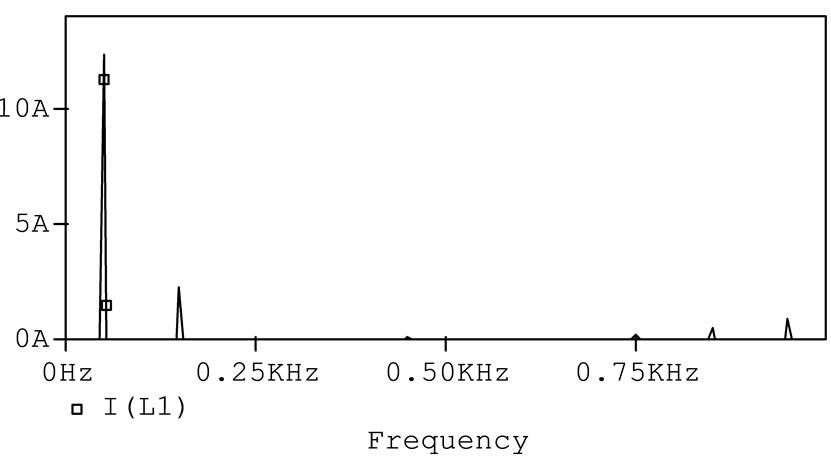
Figure 21. Load output voltage in mode 3 in resistive-inductive load, 50Hz output frequency and MI = 0.7 without using capacitor.
mode, load and modulation index on the voltage source inverter operation has been investigated. For this purpose, the equation for any operation mode of inverter is obtained and by solving them, the suitable chopping angle for removing of desired harmonic from different order are determined. It is shown that the fundamental component of output voltage is controlled by modula-tion index and variation of modulation index, influences on the output voltage harmonics. For instance, by decreasing of modulation index, the amplitude of harmonics decreased in the output voltage. It is also shown that in different modes the desired harmonic from different order removed from the output voltage. In this study also shown that the load type affected on the output voltage waveform and in the resistive-inductive loads, the output current harmonic is filtered by inductor and cause to be sinusoidal the load voltage.
7. REFERENCES
- M. Hashad and J. Iwaszkiewicz, “A Novel Orthogonal-Vectors-Based Topology of Multilevel Inverters,” IEEE Transactions on Industrial Electronics, Vol. 49, No.4, August 2002, pp. 868-874. doi:10.1109/TIE.2002.8012 34
- E. Cengelci, U. Sulistijo, O. Woo, P. Enjeti, R. Teodorescu and F. Blaabjerg, “A New Medium-Voltage PWM Inverter Topology for Adjustable-Speed Drives,” IEEE Transactions on Industry Applications, Vol. 35, May/June 1999, pp. 628-637. doi:10.1109/28.767014
- P. H. Henning, H. D. Fuchs, A. D. Le Roux and H. du T. Mouton, “Development of a 1.5 MW, Seven Level Series-stacked Converter as an APF and Regeneration Converter for a DC Traction Substation,” 36th IEEE Specialists Conference on Power Electronics 2005, Recife, 16 June 2005, pp. 2270-2276. doi:10.1109/PESC. 2005.1581948
- V. T. Somasekhar and K. Gopakumar, “Three-level In-verter Configuration Cascading Two Two-level Inver-ters,” IEE Proceedings Electric Power Applications, Vol. 150, No. 3, May 2003, pp. 245-254. doi:10.1049/ip-epa: 20030259
- R. S. Kanchan, P. N. Tekwani, M. R. Baiju, K. Gopakumar and A. Pittet, “Three-level Inverter Config-uration with Common-mode Voltage Elimination for Induction Motor Drive,” IEEE Proceedings Electric Power Applications, Vol. 152, No. 2, 4 March 2005 , pp. 261-270. doi:10.1049/ip-epa:20055034
- J.-S. Lai and F. Z. Peng, “Multilevel Convener — A New Breed of Power Converters,” IEEE Transactions on Industry Applications, Vol. 32, No. 3, 1996, pp. 509-517. doi:10.1109/28.502161
- Y. Xiong, D. Chen, S. Deng and Z. Zhang, “A New Single-phase Multilevel Current-source Inverter,” Power Electronics Conference and Exposition, Vol. 3, 2004, pp. 1682-1685.
- L. M. Fernando, F. M. Antunes, H. A. C. Braga and I. Barbi, “Application of a Generalized Current Multilevel Cell to a Current Source Inverter,” IEEE Transactions on Industrial Electronics, Vol. 46, No. 1, February 1999, pp. 31-38. doi:10.1109/41.744373
- S. Daher, R. Silva and F. Antunes, “Multilevel Current Source Inverter — The Switching Control Strategy for High Power Application,” Proceedings of the 1996 IEEE IECON 22nd International Conference on Industrial Electronics, Control, and Instrumentation, Vol. 3, 5-10 August 1996, pp. 1752-1757.
- J. Bao, D. G. Holmes, Z. Bai, Z. Zhang and D. Xu, “PWM Control of a 5-level Single-Phase Current-source Inverter with Controlled Intermediate DC-link Current,” Power Electronics Specialists Conference, Jeju, 18-22 June 2006, pp. 1-6.
- C.-M. Young, S.-F. Wu and Y.-Z. Liu “Implementation of a Multi-level Inverter Based on Selective Harmonic Elimination and Zig-Zag Connected Transformers”, The Eighth International Conference on Power Electronics and Drive Systems, Taibei, 2-5 November, 2009, pp. 387-392.
- Y. Xiong, Y. Li, X. Yang, Z. Zhang and K. Wei, “A new Three-Phase Five-level Current-source Inverter,” Applied Power Electronics Conference and Exposition, Vol. 1, 6-10 March 2005, pp. 424-427.
- J. R. Espinoza, L. A. Moran, J. I. Guzman, “Multi-Level Three-Phase Current Source Inverter Based AC Drive for High Performance Applications,” Power Electronics Specialists Conference, 2005, pp. 2553-2559.
- D. Xu and B. Wu, “Multilevel Current Source Inverters with Phase Shifted Trapezoidal PWM,” Power Elec-tronics Specialists Conference, 2005, pp. 2540-2546.
- S. Kwak and H. A. Toliyat, “Multilevel Converter Topo-logy Using Two Types of Current-Source Inverters,” IEEE Transactions on Industry Applications, Vol. 42, No. 6, 2006, pp. 1558-1564. doi:10.1109/TIA.2006. 882645
- H. F. Farahani and F. Rashidi, “A Novel Method for Selective Harmonic Elimination and Current Control in Multilevel Current Source Inverters,” International Review of Electrical Engineering-Part A, Vol. 5, No. 2, April 2010.
- H. R. Karshenas, H. A. Kojori, S. B. Dewan and J. H. Choi, “Generalized Techniques of Selective Harmonic Elimination and Current Control in Current Source Inverters/Converters,” Applied Power Electronics Conference and Exposition, Vol. 1, 1994, pp. 13-17.
- J. R. Espinoza, G. Joos, J. I. Guzman, L. A. Moran and R. P. Burgos, “Selective Harmonic Elimination and Current/Voltage Control in Current/Voltage-source
- Topologies: A Unified Approach,” IEEE Transactions on Industrial Electronics, Vol. 48, No. 1, 2001, pp. 71-81. doi:10.1109/41.904556
- H. Sarabadani and H. F. Farahani, “A Novel Method for Selective Harmonic Elimination and Voltage Control in Multilevel Voltage Source Inverters,” International Con-ference: Electrical Energy and Industrial Electronic Sy-stems, Penang, 7-8 December 2009.
- H. F. Farahani, “Investigation of Modulation Index, Operational Mode and Load Type on the SHEM Current Source Inverter,” Journal of Applied Science, 2008.
- H. F. Farahani and F. Rashidi, “A Novel Method for Selective Harmonic Elimination and Current Control in Multilevel Current Source Inverters,” International Re-view of Electrical Engineering-Part A, February 2010.
- H. Sarabadani and H. Feshki Farahani, “A Novel Method for Selective Harmonic Elimination and Voltage Control in Multilevel Voltage Source Inverters,” International Conference: Electrical Energy and Industrial Electronic Systems, Penang, 7-8 December 2009.