Intelligent Control and Automation
Vol. 3 No. 4 (2012) , Article ID: 24885 , 14 pages DOI:10.4236/ica.2012.34043
Stable Adaptive Fuzzy Control with Hysteresis Observer for Three-Axis Micro/Nano Motion Stages
Department of Mechanical Engineering, National Chung Hsing University, Taichung, Chinese Taipei
Email: lclin@mail.nchu.edu.tw
Received July 31, 2012; revised August 31, 2012; accepted September 7, 2012
Keywords: Micro/Nano Stage; Adaptive Fuzzy Control; Hysteresis Observer; Fuzzy Function Approximator
ABSTRACT
This paper considers the analytical dynamics with simplified Dahl hysteresis model for a three-axis piezoactuated micro/ nano flexure stage. An adaptive controller with nonlinear dynamic hysteresis observer is proposed using Lyapunov stability theory. In the controller, a fuzzy function approximator with parameters update law is included to compensate for the identification inaccuracy, model uncertainty, and flexure coupling effects. Simulation results are used to demonstrate the control performance.
1. Introduction
Recently, control of micro/nano stages considering the piezoactuator hysteresis effects has found great interests in the literature. Effective ultrafine-resolution trajectory tracking performance of stages is limited by the intrinsic hysteretic behavior of the piezoceramic material and the structural vibration of the devices [1].
Many efforts were trying to decrease the hysteresis effect of piezoactuators. Newcomb and Flinn [2] found that the relationship between the extension of a piezoceramic actuator and its applied electric charge has significantly less hysteresis nonlinearity than that between deformation and applied voltage. Furutani et al. [3] proposed an induced charge feedback control for the piezoactuators. The approach needs measurement of the induced charge and a specially designed charge drive amplifier, and will cause an increase in the response time of the actuator.
In order to linearize the control system, many researches focused on the inverse feedforward compensation based on some inverse hysteresis model. Several models have been suggested for describing the complex hysteretic behavior, for example, the Preisach model in Ge and Jouaneh [4,5], Yu et al. [6], and Liu et al. [7], the generalized Preisach model in Ge and Jouaneh [8], the dynamic Preisach model in Yu et al. [9]; the generalized Maxwell elasto-slip model in Goldfarb and Celanovic [10]; the variable time-relay hysteresis model in Tsai and Chen [11]; the Prandtl-Ishlinskii (PI) model (a subclass of the Preisach model) in Ang. et al. [1] and Hassani and Tjahjowidodo [12]; the Duhem model in Stepanenko and Su [13]; the polynomial approximation method in Croft and Devasia [14]; and the Jiles-Atherton model in Dupre et al. [15]. Ge and Jouaneh [5] proposed a PID feedback control using the classical Preisach model for the hysteresis. Song et al. [16] proposed a cascaded PD/lead-lag feedback controller based on a linear model for the piezoactuator with hysteresis being compensated via the feedforward cancellation using the inverse classical Preisach model. Recently, Maslan et al. [17] presented a discrete-time transfer function and its inverse for a highly nonlinear and hysteretic piezoelectric actuator, and traditional PID controller and PID with active force control were considered.
To mitigate the effects of the unknown hysteresis, Wang et al. [18] suggested a model reference control for linear systems with unknown input hysteresis using an inverse KP (Krasnosel’skii-Pokrovskii) hysteresis model [19]. Hwang et al. [20] proposed a neural-network nonlinear model for learning the hysteretic behavior of a piezoelectric actuator, and suggested a discrete-time variable-structure control for enhancing the nonlinear model-based feedforward control performance. Based on the learned nonlinear model of piezoelectric actuator systems in [20], Hwang and Jan [21] proposeed a controller including a nonlinear inverse control and a discrete neuroadaptive sliding mode control using a recurrent neural network to compensate for the residue dynamic uncertainty. Wai and Su [22] presented a supervisory genetic algorithm (SGA) control system for a piezoelectric ceramic motor. The controller consists of a GA control to search an optimum control effort online via gradient descent training process and a supervisory control to stabilize the system states around a predefined bound region.
Recently, Ronkanen et al. [23] presented a two-input (velocity and voltage) one-output (current) feedforward backpropagation network to model the inverse nonlinear velocity-current relation of a piezoelectric actuator, and then introduced a feedforward charge control scheme.
Other analytical types of nonlinear differential hysteresis models include the simplified Dahl model used in Lyshevski [24], Sun and Chang [25], Sain et al. [26], and the Bouc-Wen model in Low and Guo [27], Chen et al. [28], and Gomis-Bellmunt et al. [29]. Chen et al. [28] proposed an H∞ almost disturbance decoupling robust control based on the Bouc-Wen hysteretic model. Shieh et al. [30] proposed an adaptive displacement control for a piezopositioning mechanism with the LuGre (hysteretic) friction model suggested by De Wit et al. [31]. Gu and Zhu [32] suggested a new mathematic model to describe the frequency-dependent and amplitude-dependent hysteresis in a piezoelectric actuator using a family of ellipses. These analytical hysteresis models will be much easier for precision positioning control design.
In this work, we consider the precision control of a three-axis piezoactuated micro/nano stage. An adaptive controller with simplified Dahl model-based hysteresis variables observer is designed using the Lyapunov stability theory. In the adaptive controller, a fuzzy function approximator with parameters update law is included to compensate for the identification inaccuracy, model uncertainty, and flexure coupling effects. Simulation results are used for illustrating the possible control performance.
2. Dynamic Model for a Three-Axis Micro/Nano Motion Stage
The dynamic model for a single-axis piezoactuated flexure stage with analytic simplified Dahl hysteresis model is as below [24]:
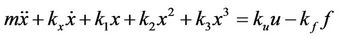 (1)
(1)
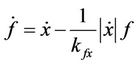 (2)
(2)
where 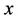 is the output displacement of the flexure stage;
is the output displacement of the flexure stage; 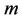 is the mass of the flexure mover;
is the mass of the flexure mover; 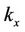 is the damping coefficient;
is the damping coefficient;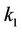 ,
,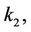 and
and  are the stiffness constants; u is the input voltage of the piezoelectric actuator;
are the stiffness constants; u is the input voltage of the piezoelectric actuator; 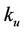 is the input gain;
is the input gain;  is the hysteresis variable;
is the hysteresis variable; 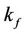 and
and 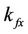 govern the scale and the shape of the hysteresis loop.
govern the scale and the shape of the hysteresis loop.
Consider a 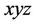 three-axis flexure micro/nano stage (P-517.3CL, Physik Instrumente, PI) [33] driven by piezoelectric actuators shown in Figure 1. The hysteresis phenomena and the coupling effects among the three axes induced by the flexure structure, can be taken into account via the following complete matrix-vector model:
three-axis flexure micro/nano stage (P-517.3CL, Physik Instrumente, PI) [33] driven by piezoelectric actuators shown in Figure 1. The hysteresis phenomena and the coupling effects among the three axes induced by the flexure structure, can be taken into account via the following complete matrix-vector model:

Figure 1. Three-axis flexure stage.
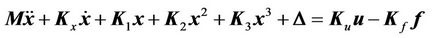 (3)
(3)
 (4)
(4)
where 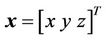 is the output displacements vector;
is the output displacements vector;

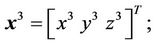

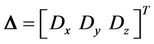
is used to consider the coupling effects among the axes and the model uncertainty;

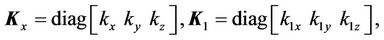

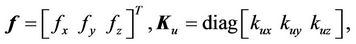
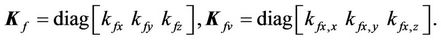
For ease of numerical simulation and implementation, the system parameters in SI units could be scaled in terms of more suitable units: displacement in nm, mass in g, time in ms, and input voltage in mV. After scaling, the scaled models keep the same forms as Equations (3) and (4). The parameters of the stage are identified, based on input/output data pairs via genetic algorithms by Chang [34], and are given as follows:

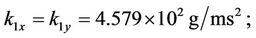
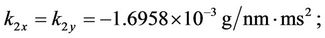
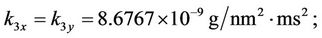
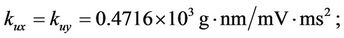
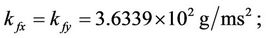
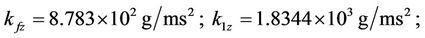
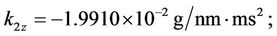

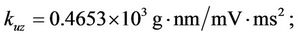

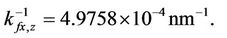
After defining the state vector as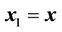 ,
,  , the stage’s dynamic model can be written in the following vector state equations:
, the stage’s dynamic model can be written in the following vector state equations:
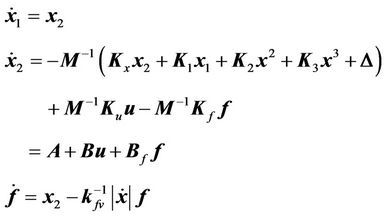 (5)
(5)
where

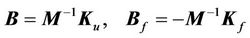
3. Stable Fuzzy Approximator-Based Adaptive Control for Micro/Nano Stages
3.1. Control Design Using Backstepping Method
Based on the nonlinear dynamics model (5), this subsection considers the backstepping-based stable control law design for the three-axis flexure stage.
First consider the  subsystem,
subsystem, . Let
. Let
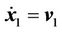 (6)
(6)
where 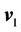 is a virtual input. Define the tracking error signal as
is a virtual input. Define the tracking error signal as
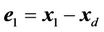 (7)
(7)
where is the desired trajectory for the three-axis motion. Differentiating Equation (7), we have
is the desired trajectory for the three-axis motion. Differentiating Equation (7), we have
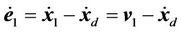 (8)
(8)
Considering the Lyapunov function candidate
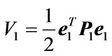 (9)
(9)
where 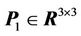 is symmetric and positive definite, and differentiating Equation (9), we have
is symmetric and positive definite, and differentiating Equation (9), we have
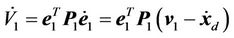 (10)
(10)
Thus, we can choose the virtual input 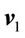 as
as
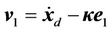 (11)
(11)
with positive definite feedback gain matrix
 such that
such that
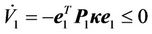 (12)
(12)
and 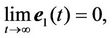 that is, the subsystem is asymptotically stable.
that is, the subsystem is asymptotically stable.
Further, the actual whole nonlinear system is considered:
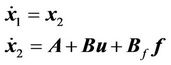 (13)
(13)
After introducing new error signal
 (14)
(14)
we can obtain
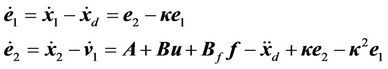 (15)
(15)
Then by considering the Lyapunov function candidate as
 (16)
(16)
where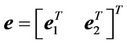 ,
,  ,
, 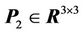
is symmetric and positive definite, and taking the time derivative of Equation (16), we have
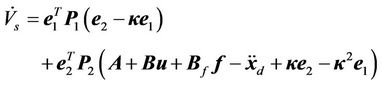 (17)
(17)
Thus we can choose the nonlinear control law as follows:
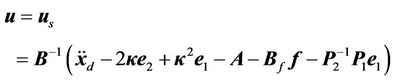 (18)
(18)
and obtain
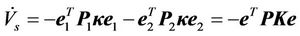 (19)
(19)
where 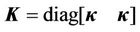 .
.
If further choose 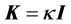 with
with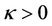 , then we can have
, then we can have
 (20)
(20)
and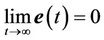 . Thus, the equilibrium point
. Thus, the equilibrium point 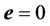 of the closed-loop system is exponentially stable.
of the closed-loop system is exponentially stable.
The internal state variables  can also be shown to be bounded. Consider the Lyapunov function
can also be shown to be bounded. Consider the Lyapunov function
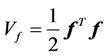 (21)
(21)
By choosing the class-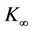 functions
functions
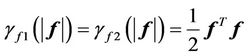 then since
then since
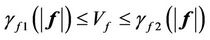 , (22)
, (22)
we know that  is positive definite, decrescent, and radially unbounded [35]. Differentiating Equation (21) and substituting in the internal dynamics
is positive definite, decrescent, and radially unbounded [35]. Differentiating Equation (21) and substituting in the internal dynamics
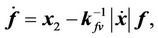 (23)
(23)
we have
 (24)
(24)
Since 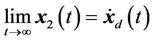
if the desired trajectory satisfies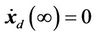 , then we can have
, then we can have 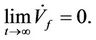 Thus, f is bounded and the overall closed-loop system is stable.
Thus, f is bounded and the overall closed-loop system is stable.
Let the output vector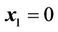 ,
, 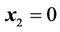 , we can obtain the system’s zero dynamics as follows:
, we can obtain the system’s zero dynamics as follows:
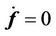 (25)
(25)
That is, the hysteresis variables will become constants when the flexure mover returns to the origin and remains there.
In order to further enhance the system’s active damping capability, we can introduce a nonlinear damping term

where 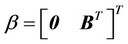 into the control law (18). That is, the control law can be modified as
into the control law (18). That is, the control law can be modified as
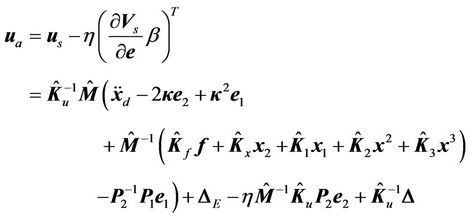 (26)
(26)
where 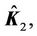
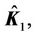

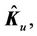
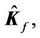
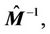 and
and 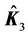 are the nominal matrices for
are the nominal matrices for 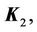

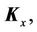


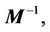 and
and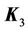 , respectively, obtained by substituting in the estimated parameters, and
, respectively, obtained by substituting in the estimated parameters, and  represents the discrepancy due to the estimate error. Let
represents the discrepancy due to the estimate error. Let 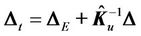 be the integral uncertainty, we can further design a fuzzy function approximator
be the integral uncertainty, we can further design a fuzzy function approximator 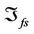 to compensate for its effect. The modified control law can be written as follows:
to compensate for its effect. The modified control law can be written as follows:
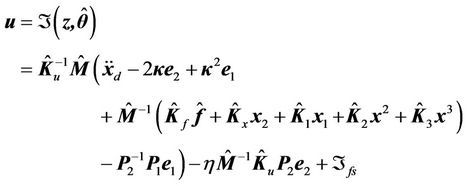 (27)
(27)
where 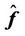 is the observed hysteresis vector for
is the observed hysteresis vector for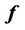 , z is the input vector of the controller, and
, z is the input vector of the controller, and 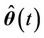 is the parameters vector to be updated for the fuzzy compensator. Here
is the parameters vector to be updated for the fuzzy compensator. Here
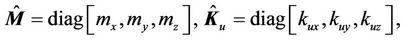
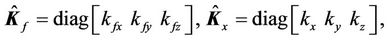

and
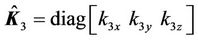
are used in Equation (27). The hysteresis observer and the fuzzy compensator design will be considered in the sequel.
3.2. Hysteresis Observer Design
Since the hysteresis variables are difficult to measure for feedback, a nonlinear observer can be suggested as:
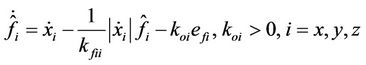 (28)
(28)
where  are the estimated hysteresis variables,
are the estimated hysteresis variables, 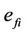 are the observer’s input variables to be defined later in the derivation of the stable control law and parameters update law, and
are the observer’s input variables to be defined later in the derivation of the stable control law and parameters update law, and 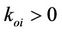 are the input gains. Define estimate errors as
are the input gains. Define estimate errors as
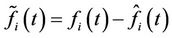 we have
we have
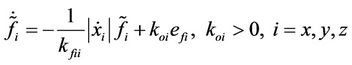 (29)
(29)
And Equation (29) can be written in the following vector form:
 (30)
(30)
where

is the estimate error vector, and
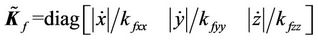 ,
,

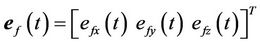 .
.
3.3. Fuzzy Function Approximators Design
This subsection will construct the fuzzy function approximators using T-S fuzzy systems to compensate for the modeling errors and coupling effects among the three axes. The tracking errors 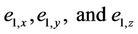 are chosen respectively as the input variable of the fuzzy approximator for each axis, and the compensating voltage of each axis is the output variable. In the universe of discourse of each input variable, five fuzzy sets are defined as in Figure 2. The rule base of the fuzzy approximator for the i-th (
are chosen respectively as the input variable of the fuzzy approximator for each axis, and the compensating voltage of each axis is the output variable. In the universe of discourse of each input variable, five fuzzy sets are defined as in Figure 2. The rule base of the fuzzy approximator for the i-th (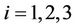 ) axis is considered as follows: Rule j: If
) axis is considered as follows: Rule j: If 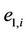 is
is 
Then
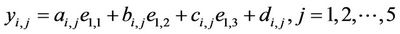 (31)
(31)
where  are the fuzzy sets defined over the universe of discourse of each input variable
are the fuzzy sets defined over the universe of discourse of each input variable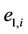 ,
, 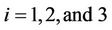 , stands for the
, stands for the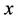 , y, and
, y, and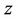 axis, respectively.
axis, respectively.
Using singleton fuzzifier, product inference engine, and center average defuzzifier [36], the mapping of the fuzzy approximator for the i-th axis is
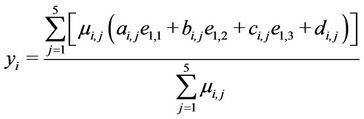 (32)
(32)
where 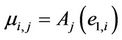 is the degree of firing of the j-th rule’s antecedent. Let
is the degree of firing of the j-th rule’s antecedent. Let

Figure 2. Membership functions for each axis.
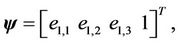
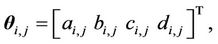
then
 (33)
(33)
Defining the regressor vector

and the unknown parameter vector
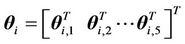 Equation (33) can be written as
Equation (33) can be written as
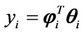 (34)
(34)
And the fuzzy approximators for the three axes can be written in the vector form as
 (35)
(35)
where

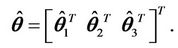
3.4. Derivation of Parameters Update Law and Stability of Overall System
In this subsection, the input signals

of the hysteresis observer, and the parameters update laws of the fuzzy function approximators will be selected in the stability consideration of the overall adaptive feedback control system for a three-axis piezoelectric flexure stage.
Consider the following Lyapunov function candidate,
 (36)
(36)
where 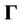 is symmetric and positive definite,
is symmetric and positive definite, 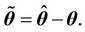 Taking the time derivative, we have
Taking the time derivative, we have
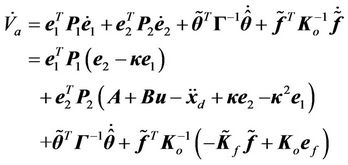 (37)
(37)
After substituting in Equations (30) and (17), Equation (37) becomes (38).
Let
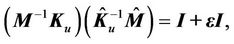

where
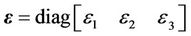
and
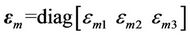
are the error matrices, 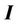 is the identity matrix. Since
is the identity matrix. Since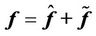 , where
, where
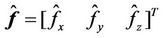 we have
we have
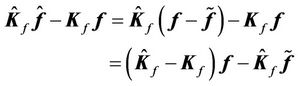 and Equation (38) can be written as
and Equation (38) can be written as
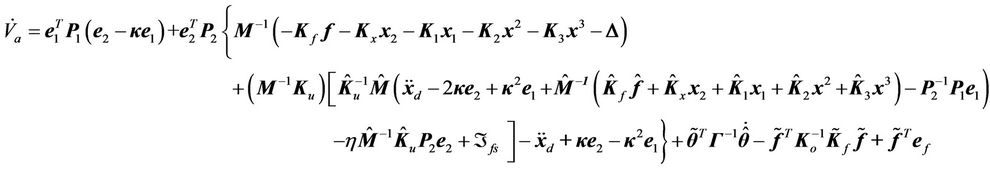 (38)
(38)
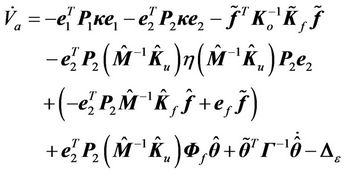 (39)
(39)
where 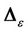 is defined as (40).
is defined as (40).
Choosing the input vector of the hysteresis observer  as:
as:
 (40)
(40)
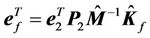 (41)
(41)
That is,
 (42)
(42)
we can obtain
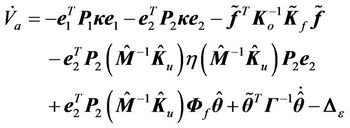 (43)
(43)
By further representing the uncertainty as:

and substituting
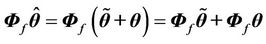
in Equation (43), we have
 (44)
(44)
Thus, we can choose the parameters adaptation law of the fuzzy approximators as:
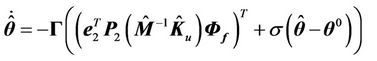 (45)
(45)
If further choose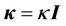 ,
, 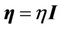 , and assume the approximation error
, and assume the approximation error 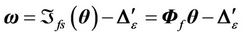 be bounded, i.e.,
be bounded, i.e., 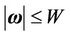 , then we can obtain
, then we can obtain
 (46)
(46)
Letting
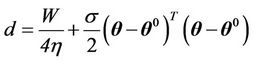 (47)
(47)
and defining 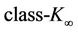 functions:
functions:
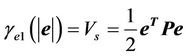 and
and 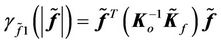 Equation (46) can be rewritten as
Equation (46) can be rewritten as
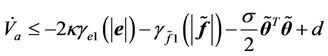 (48)
(48)
Hence, when 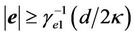
or 
or 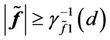 ,
, 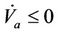 and thus the overall adaptive control system is boundedly stable.
and thus the overall adaptive control system is boundedly stable.
4. Results and Discussion
In this section computer simulation will be used to illustrate the performance of the proposed adaptive fuzzy control with hysteresis observer for a three-axis flexure stage. Triangular uncertainties for the x, y, and z axes ( ) shown in Figure 3 are selected in the simulation. The desired trajectories for the x, y, and z axes are selected as follows (t in ms):
) shown in Figure 3 are selected in the simulation. The desired trajectories for the x, y, and z axes are selected as follows (t in ms):
 (a)
(a)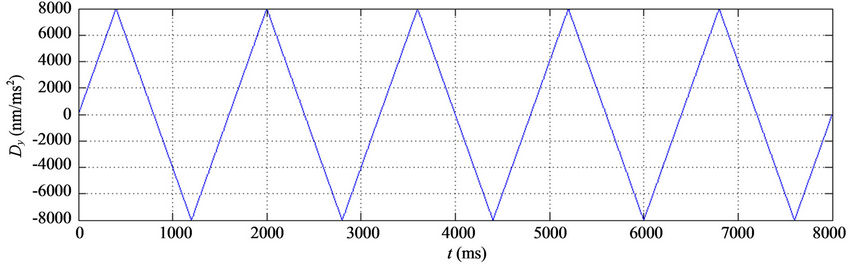 (b)
(b)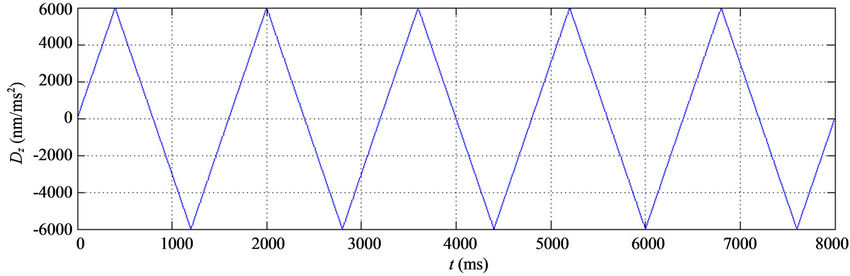 (c)
(c)
Figure 3. Triangular uncertainties for the x, y, and z axes. (a) Dx, (b) Dy, (c) Dz.

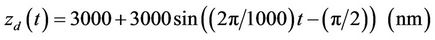
Controller parameters are selected as follows:
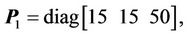
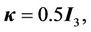
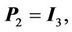
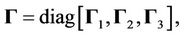
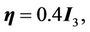

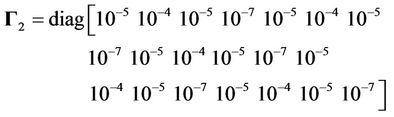

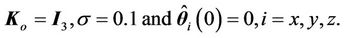
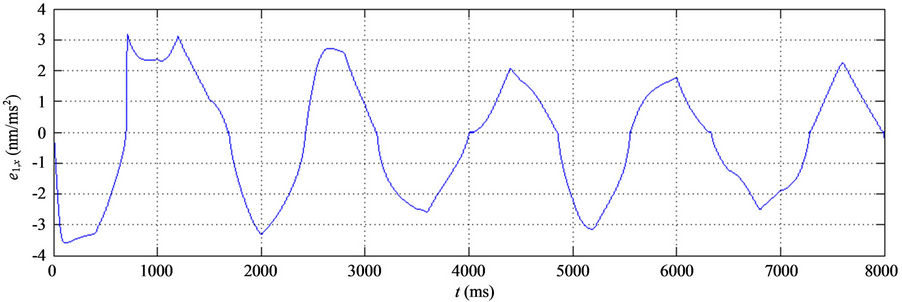
The simulation results are shown in Figure 4. From Figures 4(a)-(c), we know that the tracking performances are very good. The tracking errors of xand y-axes are within –2.5 nm - 2.2 nm, and the tracking error of z-axis is within ±2 nm. From Figures 4(d)-(f), the hysteresisvariable estimate errors of xand y-axes are within ±0.5 nm, and the estimate error of z-axis is within ±1 nm. The control voltages  are shown in Figure 4(g), and the fuzzy compensation voltages
are shown in Figure 4(g), and the fuzzy compensation voltages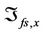 ,
, 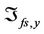 , and
, and 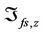 are shown in Figure 4(h). And the parameters update processes of the function approximators for x-, y-, and z-axes are shown in Figures 4(i)-(k), respectively. The parameters of the first and fifth rules are not updated since the tracking errors are small and they are nearly not fired. Although the persistent exciting of the system signals of this considered simulation case are not sufficient enough to let the other parameters converge to constants, the adaptive control system can guarantee the tracking control performance to be still very good.
are shown in Figure 4(h). And the parameters update processes of the function approximators for x-, y-, and z-axes are shown in Figures 4(i)-(k), respectively. The parameters of the first and fifth rules are not updated since the tracking errors are small and they are nearly not fired. Although the persistent exciting of the system signals of this considered simulation case are not sufficient enough to let the other parameters converge to constants, the adaptive control system can guarantee the tracking control performance to be still very good.
5. Conclusion
In this work, a stable adaptive control law with nonlinear dynamic hysteresis observer for a three-axis flexure stage
 (a)
(a)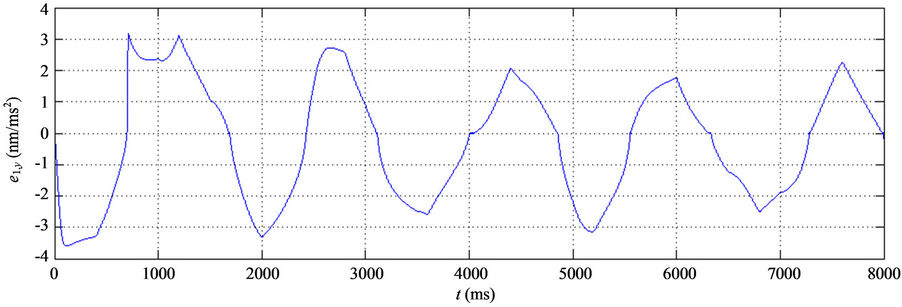 (b)
(b) (c)
(c) (d)
(d)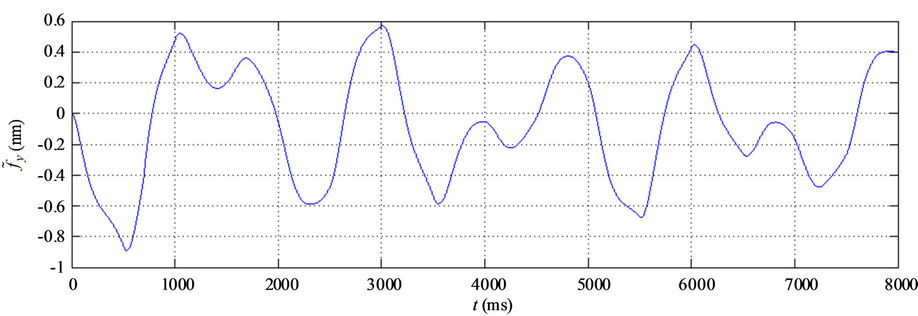 (e)
(e)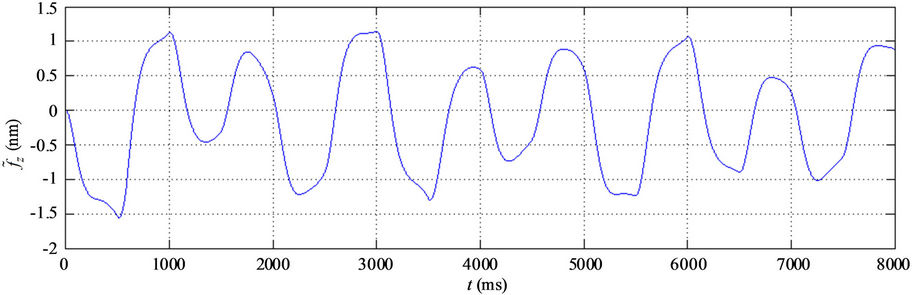 (f)
(f)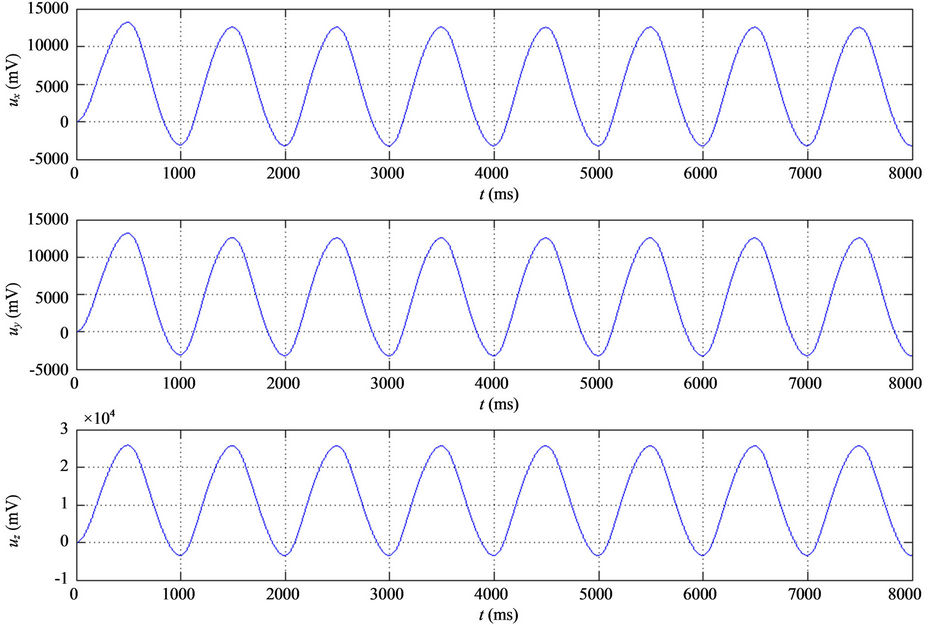 (g)
(g) (h)
(h) (i)
(i) (j)
(j) (k)
(k)
Figure 4. Control results. (a) x-axis, (b) y-axis, (c) z-axis tracking errors; Hysteresis estimate errors, (d)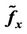 ; (e)
; (e)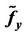 ; (f)
; (f)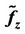 ; (g) Control voltages
; (g) Control voltages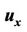 ,
, 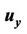 and
and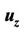 ; (h) Compensating voltages
; (h) Compensating voltages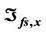 ,
, 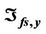 and
and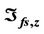 ; Parameters adaptation process (i) x-axis; (j) y-axis; (k) z-axis.
; Parameters adaptation process (i) x-axis; (j) y-axis; (k) z-axis.
is proposed. Fuzzy function approximators are included in the control law to compensate for the identification inaccuracy, model uncertainty, and flexure coupling effect. The stability of the overall closed-loop system is guaranteed using the Lyapunov theory. Simulation results are shown to illustrate the effectiveness of the suggested control approach. In the future study, actual implementation can be considered for the development of a precision stage for testing the control performance.
REFERENCES
- W. T. Ang, P. K. Khosla and C. N. Riviere, “Feedforward Controller with Inverse Rate-Dependent Model for Piezoelectric Actuators in Trajectory-Tracking Applications,” IEEE/ASME Transactions on Mechatronics, Vol. 12, No. 2, 2007, pp. 134-142. doi:10.1109/TMECH.2007.892824
- C. Newcomb and I. Flinn, “Improving the Linearity of Piezoelectric Ceramic Actuators,” Electronics Letters, Vol. 18, No. 11, 1982, pp. 442-444. doi:10.1049/el:19820301
- K. Furutani, M. Urushibata and N. Mohri, “Displacement Control of Piezoelectric Element by Feedback of Induced Charge,” Nanotechnology, Vol. 9, No. 2, 1998, pp. 93-98. doi:10.1088/0957-4484/9/2/009
- P. Ge and M. Jouaneh, “Modeling Hysteresis in Piezoceramic Actuators,” Precision Engineering, Vol. 17, No. 3, 1995, pp. 211-221. doi:10.1016/0141-6359(95)00002-U
- P. Ge and M. Jouaneh, “Tracking Control of a Piezoceramic Actuator,” IEEE Transactions on Control Systems Technology, Vol. 4, No. 3, 1996, pp. 209-216. doi:10.1109/87.491195
- Y. Yu, N. Naganathan and R. V. Dukkipati, “Preisach Modeling of Hysteresis for Piezoceramic Actuator System,” Mechanism and Machine Theory, Vol. 37, No. 1, 2002, pp. 49-59. doi:10.1016/S0094-114X(01)00065-9
- L. Liu, K. K. Tan, A. S. Putra and T. H. Lee, “Compensation of Hysteresis in Piezoelectric Actuator with Iterative Learning Control,” IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Suntec Convention and Exhibition Center, Singapore City, 14-17 July 2009, pp. 1300-1305.
- P. Ge and M. Jouaneh, “Generalized Preisach Model for Hysteresis Nonlinearity of Piezoceramic Actuators,” Precision Engineering, Vol. 20, No. 2, 1997, pp. 99-111. doi:10.1016/S0141-6359(97)00014-7
- Y. Yu, Z. Xiao, N. Naganathan and R. V Dukkipati, “Dynamic Preisach Modeling of Hysteresis for the Piezoceramic Actuator System,” Mechanism and Machine Theory, Vol. 37, No. 1, 2002, pp. 75-89. doi:10.1016/S0094-114X(01)00060-X
- M. Goldfarb and N. Celanovic, “Modeling Piezoelectric Stack Actuators for Control of Micromanipulation,” IEEE Control Systems Magazine, Vol. 17, No. 3, 1997, pp. 69- 79. doi:10.1109/37.588158
- M.-S. Tsai and J.-S. Chen, “Robust Tracking Control of a Piezoactuator Using a New Approximate Hysteresis Model,” ASME Journal of Dynamic Systems, Measurement, and Control, Vol. 125, No. 1, 2003, pp. 96-102. doi:10.1115/1.1540114
- V. Hassani and T. Tjahjowidodo, “Integrated Rate and Inertial Dependent Prandtl-Ishlinskii Model for Piezoelectric Actuator,” IEEE 2nd International Conference on Instrumentation Control and Automation, Bandung, 15- 17 November 2011, pp. 35-40.
- Y. Stepanenko and C.-Y. Su, “Intelligent Control of Piezoelectric Actuators,” Proceedings of IEEE Conference on Decision and Control, Tampa, 16-18 December 1998, pp. 4234-4239.
- D. Croft and S. Devasia, “Hysteresis and Vibration Compensation for Piezoactuators,” Journal of Guidance, Control, and Dynamics, Vol. 21, No. 5, 1998, pp. 710- 717.
- L. Dupre, R. van Keer and J. A. A. Melkebeek, “Identification of the Relation between the Material Parameters in the Preisach Model and in the Jiles-Atherton Hysteresis Model,” Journal of Applied Physics, Vol. 85, No. 8, 1999, pp. 4376-4378. doi:10.1063/1.369789
- G. Song, J. Zhao, X. Zhou and J. A. De Abreu-García, “Tracking Control of a Piezoceramic Actuator with Hysteresis Compensation Using Inverse Preisach Model,” IEEE/ASME Transactions on Mechatronics, Vol. 10, No. 2, 2005, pp. 198-209. doi:10.1109/TMECH.2005.844708
- M. N. Maslan, M. Mailah and I. Z. M. Darus, “Identification and Control of a Piezoelectric Bender Actuator,” IEEE 3rd International Conference on Intelligent Systems Modeling and Simulation, Kota Kinabalu, 8-10 February 2012, pp. 461-466. doi:10.1109/ISMS.2012.100
- Y. Wang, C. Y. Su and H. Hong, “Model Reference Control Including Adaptive Inverse Hysteresis for Systems with Unknown Input Hysteresis,” Proceedings of IEEE International Conference on Networking, Sensing and Control, London, 15-17 April 2007, pp. 70-75. doi:10.1109/ICNSC.2007.372935
- M. A. Krasnosel’skii and A. V. Pokrovskii, “Systems with Hysteresis,” Springer-Verlag, Berlin, 1983.
- C. L. Hwang, C. Jan and Y. H. Chen, “Piezomechanics Using Intelligent Variable-Structure Control,” IEEE Transactions on Industrial Electronics, Vol. 48, No. 1, 2001, pp. 47-59. doi:10.1109/41.904550
- C. L. Hwang and C. Jan, “A Reinforcement Discrete Neuro-Adaptive Control for Unknown Piezoelectric Actuator Systems with Dominant Hysteresis,” IEEE Transactions on Neural Networks, Vol. 14, No. 1, 2003, pp. 66-78. doi:10.1109/TNN.2002.806610
- R. J. Wai and K. H. Su, “Supervisory Control for Linear Piezoelectric Ceramic Motor Drive Using Genetic Algorithm,” IEEE Transactions on Industrial Electronics, Vol. 53, No. 2, 2006, pp. 657-673. doi:10.1109/TIE.2006.870661
- P. Ronkanen, P. Kallio, M. Vilkko and H. N. Koivo, “Displacement Control of Piezoelectric Actuators Using Current and Voltage,” IEEE/ASME Transactions on Mechatronics, Vol. 16, No. 1, 2011, pp. 160-166. doi:10.1109/TMECH.2009.2037914
- S. E. Lyshevski, “MEMS and NEMS: Systems, Device, and Structures,” CRC Press, New York, 2002, pp. 260- 262.
- X. Sun and T. Chang, “Control of Hysteresis in a Monolithic Nanoactuator,” Proceedings of American Control Conference, Vol. 3, Arlington, 25-27 June 2001, pp. 2261-2266.
- P. M. Sain, M. K. Sain and B. F. Spencer, “Models for Hysteresis and Application to Structural Control,” Proceedings of American Control Conference, Vol. 1, Albuquerque, 4-6 June 1997, pp. 16-20.
- T. S. Low and W. Guo, “Modeling of a Three-Layer Piezoelectric Bimorph Beam with Hysteresis,” Journal of Microelectromechanical Systems, Vol. 4, No. 4, 1995, pp. 230-237. doi:10.1109/84.475550
- B. M. Chen, T. H. Lee, C.-C. Hang, Y. Guo and S. Weerasooriya, “An H∞ Almost Disturbance Decoupling Robust Controller Design for a Piezoceramic Bimorph Actuator with Hysteresis,” IEEE Transactions on Control Systems Technology, Vol. 7, No. 2, 1999, pp. 160-174. doi:10.1109/87.748143
- O. Gomis-Bellmunt, F. Ikhouane, D. Montesinos-Miracle, S. Galceran-Arellano and J. Rull-Duran, “Control of a Piezoelectric Hysteretic Actuator,” 13th European Conference on Power Electronics and Applications, Barcelona, 8-10 September 2009, pp. 1-6.
- H. J. Shieh, F. J. Lin, P. K. Huang and L. T. Teng, “Adaptive Displacement Control with Hysteresis Modeling for Piezoactuated Positioning Mechanism,” IEEE Transactions on Industrial Electronics, Vol. 53, No. 3, 2006, pp. 905-914. doi:10.1109/TIE.2006.874264
- C. C. De Wit, H. Olsson, K.J. Åström and P. Lischinsky, “A New Model for Control of Systems with Friction,” IEEE Transactions on Automatic Control, Vol. 40, No. 3, 1995, pp. 419-425. doi:10.1109/9.376053
- G. Y. Gu and L. Zhu, “Modeling Piezoelectric Actuator Hysteresis with a Family of Ellipses,” IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Montréal, 6-9 July 2010, pp. 878-883.
- Physik Instrumente (PI), “Piezo Tutorial: Nanopositioning with Piezoelectrics.” http://www.pi.ws
- B. Y. Chang, “Stable Adaptive Control for a Three-Axis Nanopositioner: Implementation Using ALTERA DSP Development Board,” Master Thesis, Department of Mechanical Engineering, National Chung Hsing University, Chung Hsing, 2005.
- J. T. Spooner, M. Maggiore, R. Ordóñez and K. M. Passino, “Stable Adaptive Control and Estimation for Nonlinear Systems: Neural and Fuzzy Approximator Techniques,” Wiley, New York, 2002. doi:10.1002/0471221139
- L.-X. Wang, “A Course in Fuzzy Systems and Control,” Prentice-Hall, Upper Saddle River, 1997.

