Materials Sciences and Applications
Vol.4 No.12(2013), Article ID:41543,8 pages DOI:10.4236/msa.2013.412106
Structural and Magnetic Properties of Mn0.50-xZn0.50CuxFe2O4
![]()
1Department of Physical Sciences, School of Engineering and Computer Science, Independent University-Bangladesh, Dhaka, Bangladesh; 2Department of Arts and Sciences, Ahsanullah University of Science and Technology, Dhaka, Bangladesh; 3Materials Science Division, Atomic Energy Centre, BAEC, Dhaka, Bangladesh; 4Department of Physics, Bangladesh University of Engineering and Technology, Dhaka, Bangladesh.
Email: *farhadiub@gmail.com; *farhad_840@yahoo.com
Copyright © 2013 F. Alam et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received October 25, 2013; revised November 27, 2013; accepted December 11, 2013
Keywords: Combustion Method; Mn-Cu-Zn Ferrites; Initial Permeability; B-H Loop
ABSTRACT
Mn0.50-xZn0.50CuxFe2O4 (where x = 0.0 - 0.3) ferrites have been synthesized by auto combustion method. X-ray diffraction patterns reveal that all compositions are of single phase cubic spinel structure. The lattice parameter decreases with the increase in Cu2+ content obeying the Vegard’s law. The bulk density, average grain size, initial permeability, Néel temperature and saturation magnetic induction of Mn0.50-xZn0.50CuxFe2O4 increased with increasing Cu2+content. It is observed that both density and initial permeability increase with increasing sintering temperature. The maximum initial permeability is found to be 1061 which is almost four times greater than that of the parent composition. The resonance frequency of all the samples shifts towards the lower frequency as the permeability increases with Cu2+ content. It is observed from B-H loops of Mn0.50-xZn0.50CuxFe2O4 that coercivity decreases and retentivity increases with Cu2+ content. Possible explanations for the observed magnetic properties with various Cu2+ contents are discussed.
1. Introduction
Polycrystalline spinel ferrites are technologically very important materials having potential applications and interesting physical properties. Mn-Zn and substituted Mn-Zn ferrites are pertinent magnetic materials due to their high permeability, high magnetization, relatively high Néel temperature, low losses, low cost and environmental stability. These ferrites have been widely used in electrical and magnetic devices for high frequency applications [1-4]. The physical and magnetic properties can be controlled by the preparation condition, chemical composition, sintering temperature and the amount of substitutions. Several investigations on the properties of Ni-Mn-Zn [5], Ni-Cu-Zn [6], Mg-Cu-Zn [7], Co-Mn-Zn [8] ferrites have been reported. It was found that the poor densification and slow grain growth rate can be remarkably improved and consequently initial permeability can be enhanced by the substitution of Cu [9]. No report has been found in the literature regarding the magnetic properties of Cu substituted Mn-Zn ferrites for Mn prepared by combustion method. In the present work, the influence of Cu2+ in place of Mn2+ on the properties of Mn-Zn ferrites has been investigated by studying the structure and some magnetic properties.
2. Experimental
The chemical compositions of Mn0.50-xZn0.50CuxFe2O4 (with x = 0.0 - 0.3 at a step of 0.1) were prepared by combustion method. The stoichiometric amounts of commercially available analytical grade powders of MnCl2·4H2O, Cu(NO3)2·3H2O, Zn(NO3)2·6H2O and Fe (NO3)3·9H2O were dissolved in ethanol to obtain a mixed homogenous solution. Ammonia solution was slowly added to adjust the pH at level 7. The solution was placed at constant temperature bath (70˚C) followed by an ignition and formed a fluffy loose powders of the desired composition. The resultant powders were calcined at 700˚C for five hours in air. The grounded fine powders were then pressed into discand toroid-shaped samples. The samples prepared from each composition were sintered at 1200˚C, 1250˚C and 1300˚C for five hours in air. During sintering, temperature ramps were 10˚C/min for heating and 5˚C/min for cooling. The structural characterization was carried out with an X-ray diffractometer using CuKα radiation (λ = 1.54178Å). The lattice parameter was determined by using the Nelson-Riley extrapolation method [10]. The lattice parameters obtained from each reflected plane were plotted against NelsonRiley function,
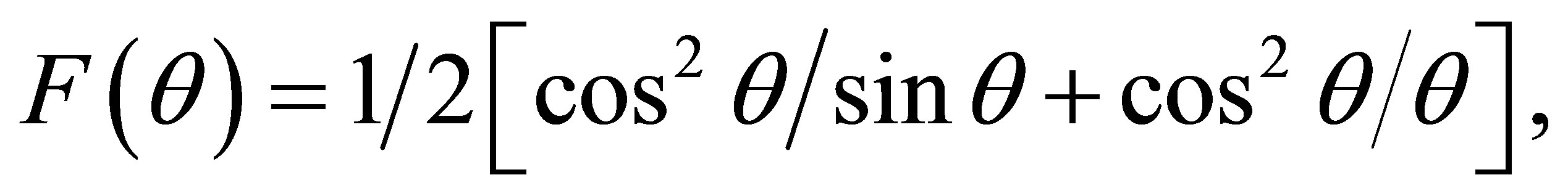
where  is the Bragg’s angle. The exact values of lattice constant, a0 were estimated from the extrapolation of the best fitted line to
is the Bragg’s angle. The exact values of lattice constant, a0 were estimated from the extrapolation of the best fitted line to 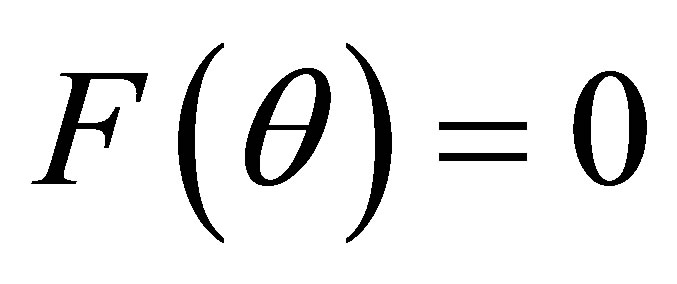 or
or  = 90˚. The bulk density,
= 90˚. The bulk density, 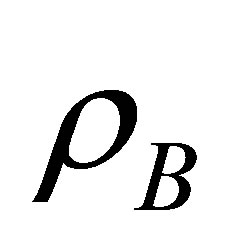 was determined using the expression
was determined using the expression  , where W and
, where W and  are the weight of the sample in air and water, respectively and ρ is the density of water at room temperature. The theoretical density,
are the weight of the sample in air and water, respectively and ρ is the density of water at room temperature. The theoretical density,  was calculated using the relation:
was calculated using the relation:  , where NA is Avogadro’s number, M is the molecular weight of the corresponding composition and Z is the number of molecules per unit cell, which is 8 for the spinel cubic structure. The porosity, P was calculated from the relation
, where NA is Avogadro’s number, M is the molecular weight of the corresponding composition and Z is the number of molecules per unit cell, which is 8 for the spinel cubic structure. The porosity, P was calculated from the relation . The micrographs of Mn0.50-xZn0.50CuxFe2O4 were taken by a Scanning Electron Microscope (SEM). From these micrographs, the average grain size (D) was estimated by the linear intercept method. The frequency and temperature dependent complex initial permeability were measured using Wayne Kerr Impedance Analyzer (Model No.6500B) in the frequency range 100 Hz - 120 MHz. The real part (
. The micrographs of Mn0.50-xZn0.50CuxFe2O4 were taken by a Scanning Electron Microscope (SEM). From these micrographs, the average grain size (D) was estimated by the linear intercept method. The frequency and temperature dependent complex initial permeability were measured using Wayne Kerr Impedance Analyzer (Model No.6500B) in the frequency range 100 Hz - 120 MHz. The real part ( ) and the imaginary part (
) and the imaginary part ( ) of the complex initial permeability were calculated using the following relations
) of the complex initial permeability were calculated using the following relations ,and
,and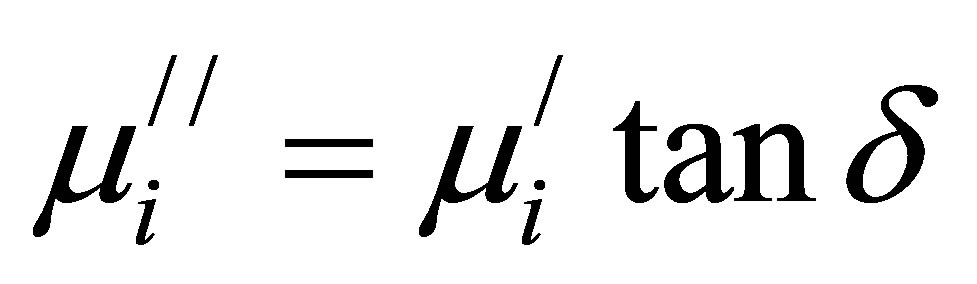 , where
, where 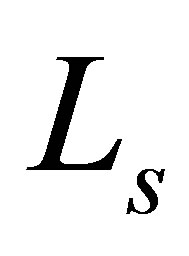 is the self inductance of the sample core and
is the self inductance of the sample core and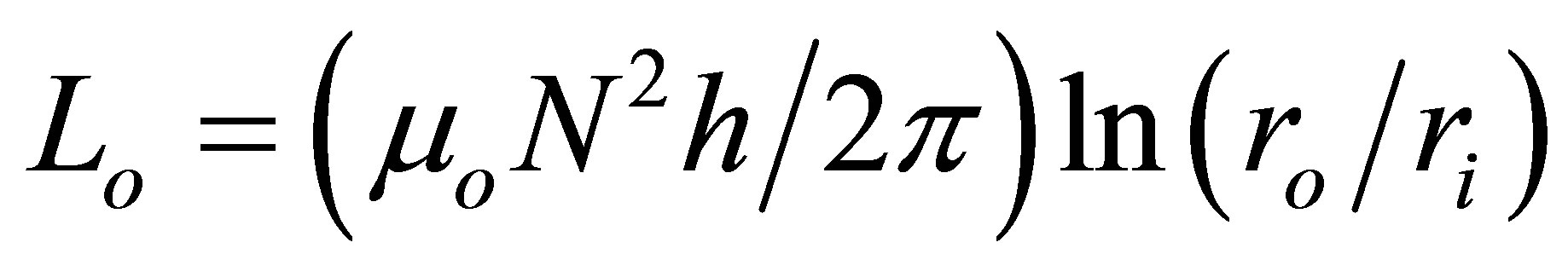 , is derived geometrically.
, is derived geometrically. 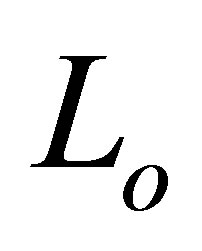 is the inductance of the winding coil without the sample core, N is the number of turns of the coil (N = 4), h is the thickness,
is the inductance of the winding coil without the sample core, N is the number of turns of the coil (N = 4), h is the thickness, 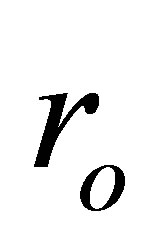 is the outer radius and
is the outer radius and 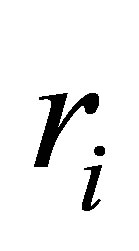 is the inner radius of the toroid-shaped sample. The relative quality factor (RQF) was calculated from the relation:
is the inner radius of the toroid-shaped sample. The relative quality factor (RQF) was calculated from the relation: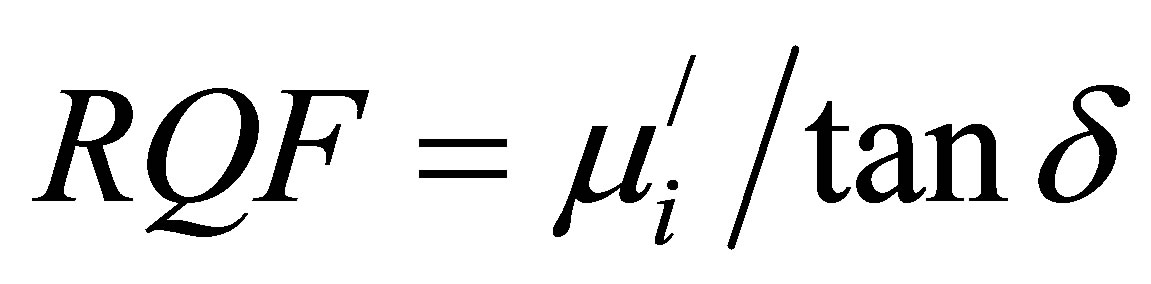 , where tand is the loss factor. B-H loops were measured at room temperature using an Automatic Magnetic Hysteresis Graph Tracer (Model no. AMH-300, Laboratorio Electrofisico).
, where tand is the loss factor. B-H loops were measured at room temperature using an Automatic Magnetic Hysteresis Graph Tracer (Model no. AMH-300, Laboratorio Electrofisico).
3. Results and Discussion
3.1. Structural Analysis of Mn0.50-xZn0.50CuxFe2O4
Figure 1 shows the X-ray diffraction (XRD) patterns for various Mn0.50-xZn0.50CuxFe2O4 (with x = 0.0 - 0.3 at a step of 0.1) sintered at 1250˚C. The positions of the peaks for the various compositions indicate a single phase cubic spinel crystal structure. It is seen that a0 decreases linearly with increasing Cu2+ content and obeys Vegard’s law [11].
The variation of a0 as a function of Cu2+ content is shown in Figure 2. The values of a0 are shown in Table 1. The decreasing a0 with Cu2+content may be explained in terms of ionic radii. As the ionic radius of Mn2+ (0.80 Å) ion is larger than that of Cu2+ (0.72 Å), a0 decreases. [8,9,12]. As the smaller Cu2+ ions replace the bigger Mn2+ ions in Mn0.50-xZn0.50CuxFe2O4, the unit cell compresses without disturbing the symmetry of lattice [13].
A similar linear variation has been reported by Ravinder et al. [14]. The r-variant for Mn0.50-xZn0.50CuxFe2O4 was calculated by the expression: r-variant = (0.50-x)rMn + xrCu ,where rMn and rCu are the radii of the Mn2+ and Cu2+ respectively. It is found that the r-variant decreases with increase in Cu2+ content which is also shown in Figure 2.
Figure 3 shows the effect of Cu2+ substitutions on  and
and 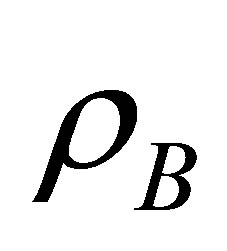 in Mn0.50-xZn0.50CuxFe2O4 sintered at various sintering temperatures, Ts. It is found that
in Mn0.50-xZn0.50CuxFe2O4 sintered at various sintering temperatures, Ts. It is found that  is larger in magnitude than corresponding
is larger in magnitude than corresponding . This is because
. This is because
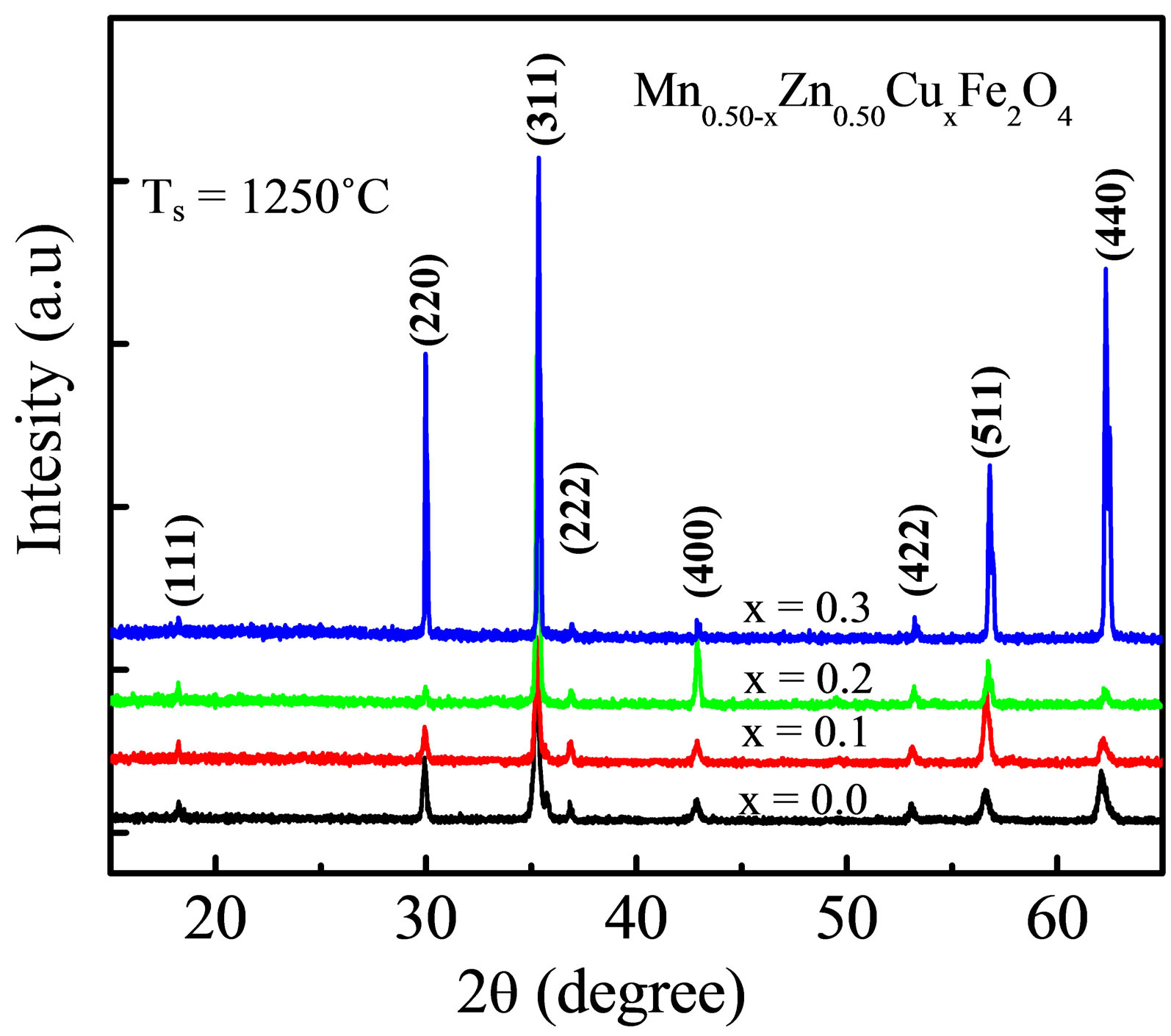
Figure 1. XRD patterns of Mn0.50-xZn0.50CuxFe2O4 sintered at 1250˚C.
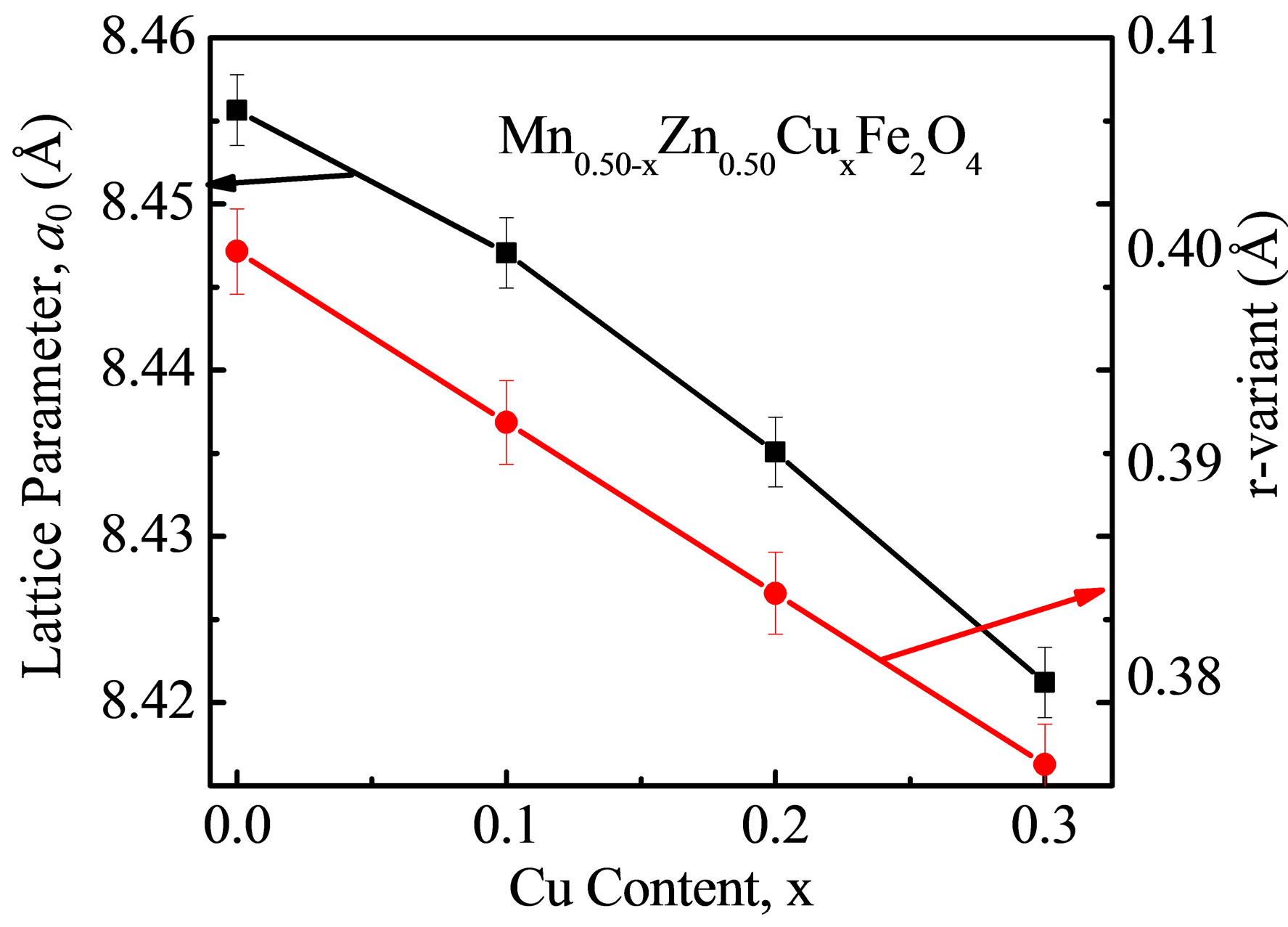
Figure 2. Variation of lattice parameter and r-variant of Mn0.50-xZn0.50CuxFe2O4 with Cu2+ content.
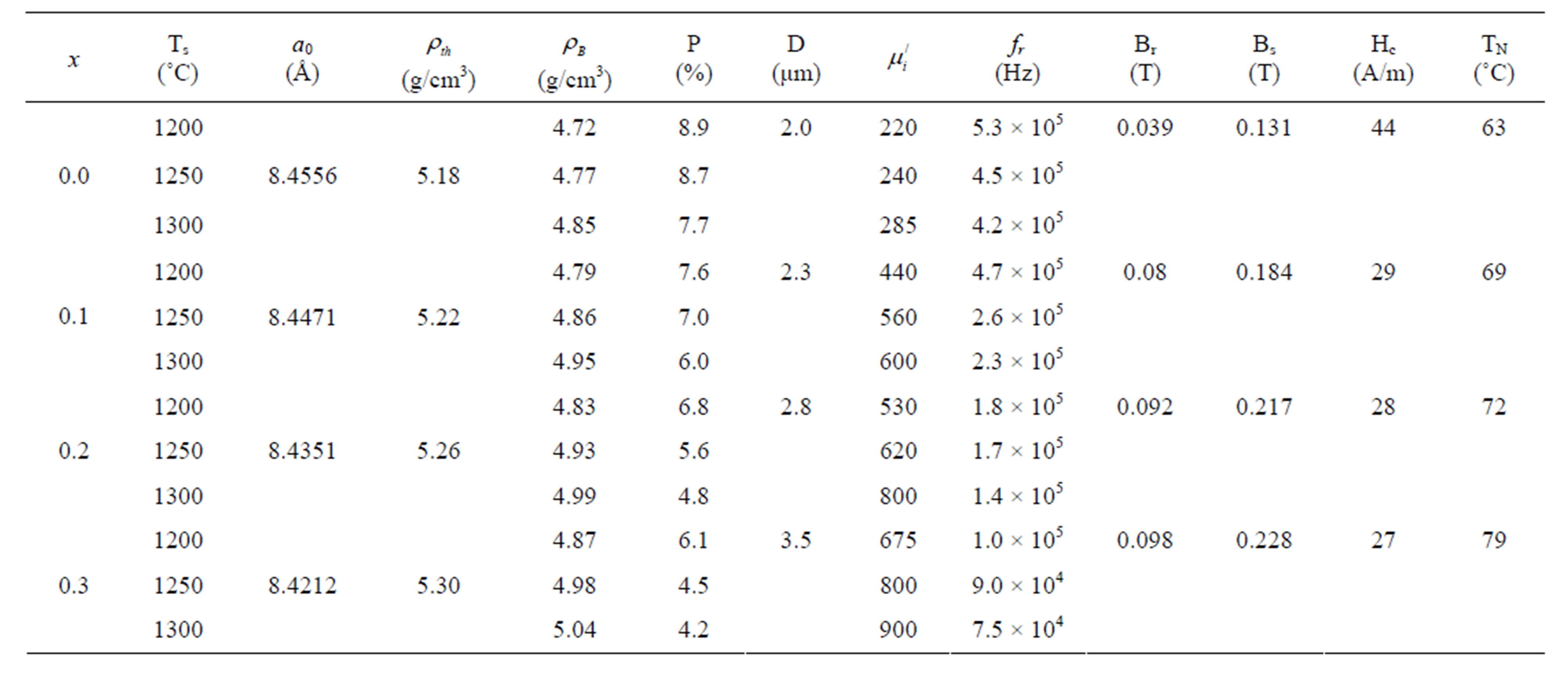
Table 1. Lattice parameter, density, porosity, average grain size, initial permeability, resonance frequency, residual and saturation inductions, coercive field and Néel temperature of various Mn0.50-xZn0.50CuxFe2O4 sintered at different sintering temperatures.
some pores may be developed in the samples during sintering process. It is also found that both ρth and ρB increase with increase in Cu2+ content while the P follows the opposite trend. The increase in ρB can be attributed to the difference in atomic weight and specific gravity of the Cu and Mn. The atomic weight and specific gravity of Cu (63.55 amu and 8.94 g·cm−3) is greater than that of Mn (55.94 amu and 7.21 g·cm−3) [15]. Also Cu2+ promotes densification of Mn0.50-xZn0.50CuxFe2O4 during low sintering temperature. These combined factors may contribute to the enhancement of ρB for various Mn0.50-xZn0.50CuxFe2O4 [16,17]. Similar results have been reported by Haque et al. [7]. On the other hand, P of Mn0.50-xZn0.50CuxFe2O4 reduces due to increasing ρB. It is revealed from Figures 3(a) and (b) that ρB increases and P decreases with increasing Ts for various Mn0.50-xZn0.50CuxFe2O4. This is because during the sintering process, the thermal energy generates a force that drives the grain boundaries to grow over pores, thereby decreasing the pore volume and increases the density of the compositions. These results agree well with the reported value [7,18]. The increase in ρB and decrease in P for various Mn0.50-xZn0.50CuxFe2O4 with the addition of Cu2+ for various Ts are tabulated in Table 1.
3.2. Microstructure of Mn0.50-xZn0.50CuxFe2O4
The scanning electron micrographs as shown in Figure 4 reveal that the grain size is influenced by the Cu2+ substitution, where the grain size increases with increase in Cu2+ content in Mn0.50-xZn0.50CuxFe2O4 sintered at 1200˚C. The D of Mn0.50-xZn0.50CuxFe2O4 varies from 2 μm to 4 μm at constant Ts.
 (a)
(a) (b)
(b)
Figure 3. Variation of (a) density and (b) porosity of Mn0.50-xZn0.50CuxFe2O4 as a function of Cu2+ content.
The values of D are presented in Table 1. Figure 5 shows the micrographs of Mn0.40Zn0.50Cu0.10Fe2O4 at different Ts. It is seen that the D increases with increasing Ts. The grain size increases with increase in Cu2+ due to the melting point of copper (1084˚C) is less than that of manganese (1246˚C). During sintering Cu2+ influences the microstructure by the formation of liquid phase. It facilitates the grain growth and grain growth reflects the competition between the driving force for grain boundary movement and the retarding force exerted by pores [19, 20]. D increases with Ts because of homogeneous grain growth.
3.3. Magnetic Properties of Mn0.50-xZn0.50CuxFe2O4
3.3.1. Frequency Dependent Complex Initial Permeability
Figure 6 shows the complex initial permeability spectra

Figure 4. Scanning electron micrographs of Mn0.50-xZn0.50CuxFe2O4 sintered at 1200˚C.

Figure 5. Scanning electron micrographs of Mn0.40Zn0.50Cu0.10Fe2O4 for various sintering temperatures.
for all Mn0.50-xZn0.50CuxFe2O4 (where x = 0.0 to 0.3 at a step of 0.1) sintered at 1200˚C, 1250˚C and 1300˚C, respectively as a function of frequency.
The complex permeability is given by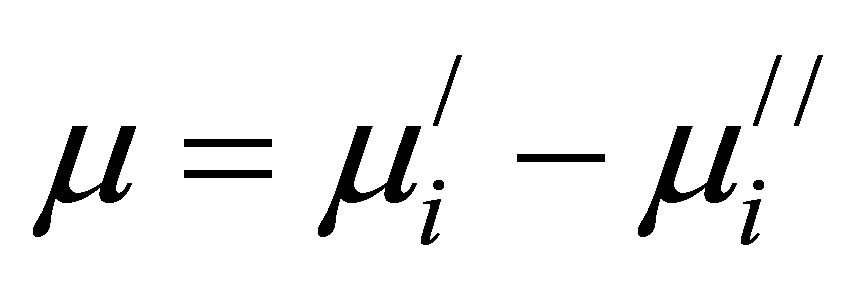 . Here
. Here 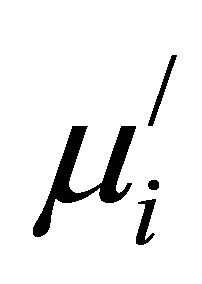 describes the stored energy expressing the component of magnetic induction B in phase and
describes the stored energy expressing the component of magnetic induction B in phase and  describes the dissipation of energy expressing the component 90˚ out of phase with the alternating magnetic field H. It is found that
describes the dissipation of energy expressing the component 90˚ out of phase with the alternating magnetic field H. It is found that 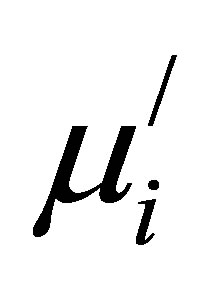 increases with increasing Cu2+ content for various Mn0.50-xZn0.50CuxFe2O4 at constant Ts. It is also observed that
increases with increasing Cu2+ content for various Mn0.50-xZn0.50CuxFe2O4 at constant Ts. It is also observed that 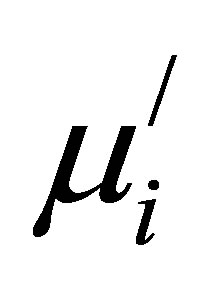 increases with increasing Ts. Highest
increases with increasing Ts. Highest  was obtained 1061 for Mn0.20Zn0.50Cu0.30Fe2O4 at frequency 103 Hz sintered at 1300˚C.
was obtained 1061 for Mn0.20Zn0.50Cu0.30Fe2O4 at frequency 103 Hz sintered at 1300˚C. 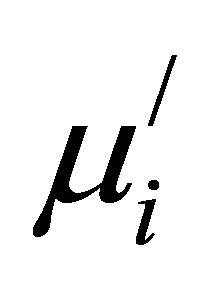 remains almost constant in the frequency range up to a certain frequency, which is called the resonance frequency, fr. There is a decrease in
remains almost constant in the frequency range up to a certain frequency, which is called the resonance frequency, fr. There is a decrease in 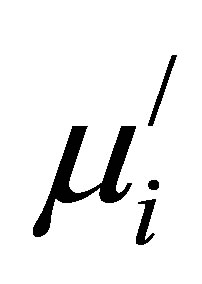 and increase in
and increase in 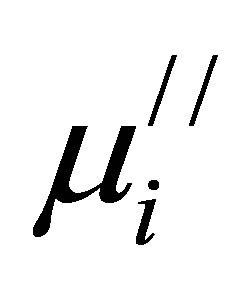 above fr observed for various Mn0.50-xZn0.50CuxFe2O4. The fr is the range of frequency of the compositions up to which these can be used efficiently. The values of
above fr observed for various Mn0.50-xZn0.50CuxFe2O4. The fr is the range of frequency of the compositions up to which these can be used efficiently. The values of 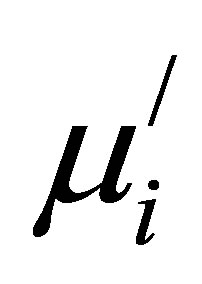 and fr for all samples sintered at various Ts are presented in Table 1.
and fr for all samples sintered at various Ts are presented in Table 1.
It is observed from Figure 7 that the  increases and fr shifted towards the lower frequency with Cu2+ in Mn0.50-xZn0.50CuxFe2O4 at different Ts. The increasing
increases and fr shifted towards the lower frequency with Cu2+ in Mn0.50-xZn0.50CuxFe2O4 at different Ts. The increasing 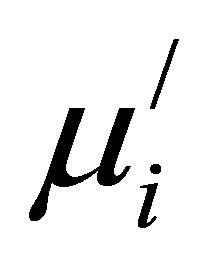 and shifting fr to lower frequency at constant Ts
and shifting fr to lower frequency at constant Ts
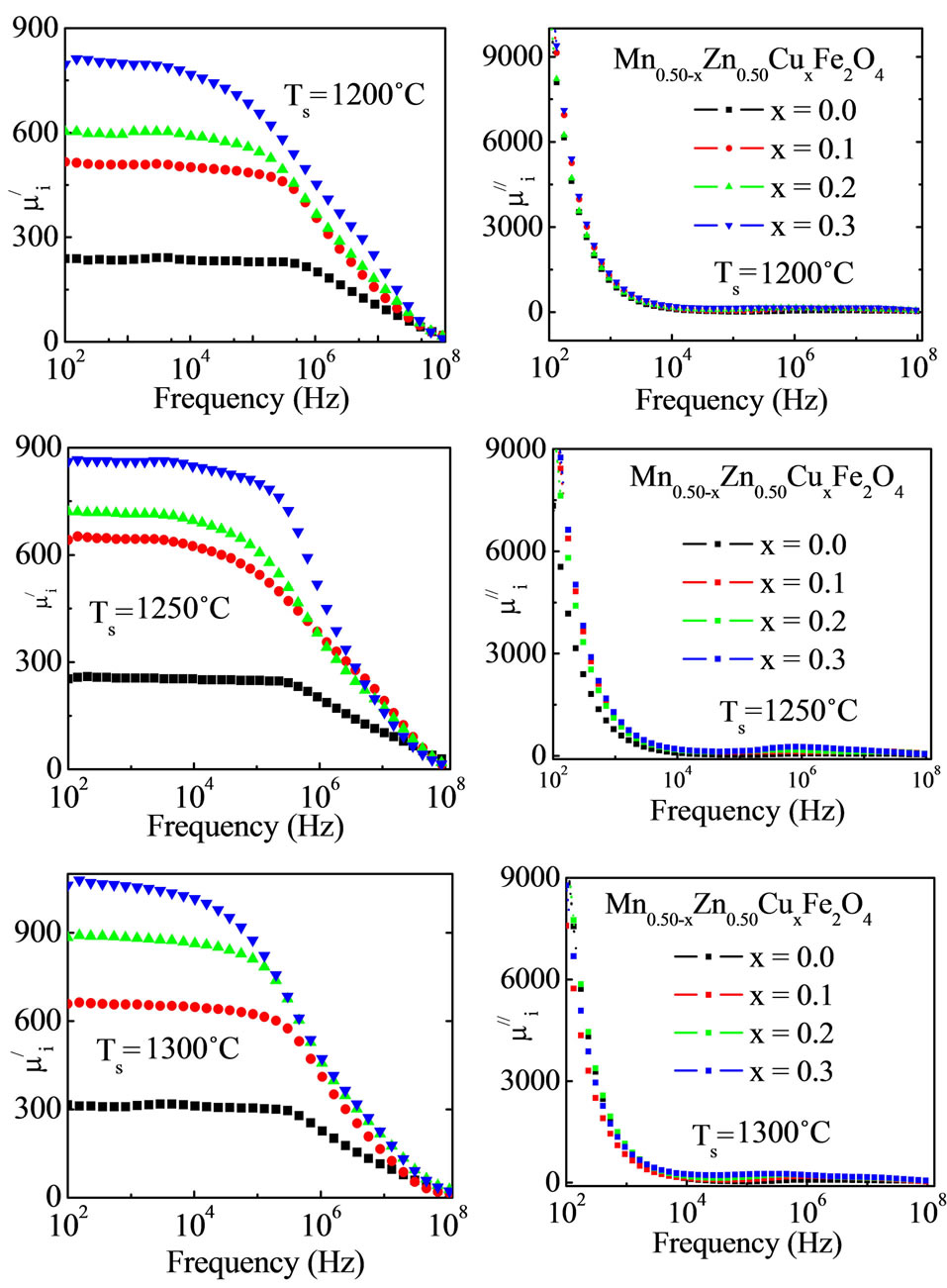
Figure 6. Frequency dependent Complex initial permeability of Mn0.50-xZn0.50CuxFe2O4 at various Ts.
follows the Snoek’s relation [21]. The 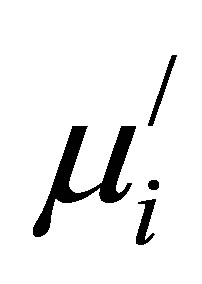 of ferrites depends on many factors like reversible domain wall displacement, the amount and the type of dopant ions, D and intragranular porosity, etc [22-24]. It is well known that
of ferrites depends on many factors like reversible domain wall displacement, the amount and the type of dopant ions, D and intragranular porosity, etc [22-24]. It is well known that 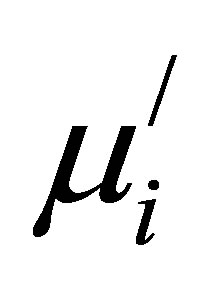 of polycrystalline ferrite is related to two magnetizing mechanisms: domain wall motion and spin rotation [25-27]. Globus et al. [22] studied several Ni-Zn ferrites and found a linear relationship between
of polycrystalline ferrite is related to two magnetizing mechanisms: domain wall motion and spin rotation [25-27]. Globus et al. [22] studied several Ni-Zn ferrites and found a linear relationship between 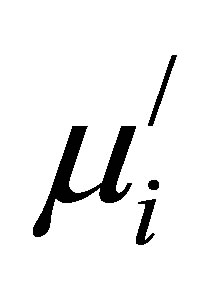 and D. Kakaktar et al. [28] studied the effect of D on
and D. Kakaktar et al. [28] studied the effect of D on 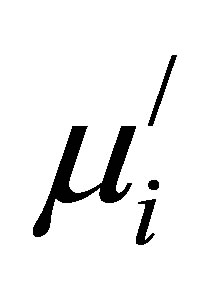 and found that
and found that 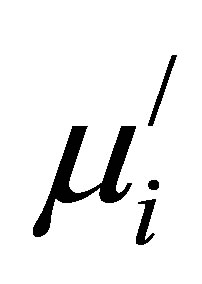 µD. The
µD. The  can be expressed by Globus-Duplex relation
can be expressed by Globus-Duplex relation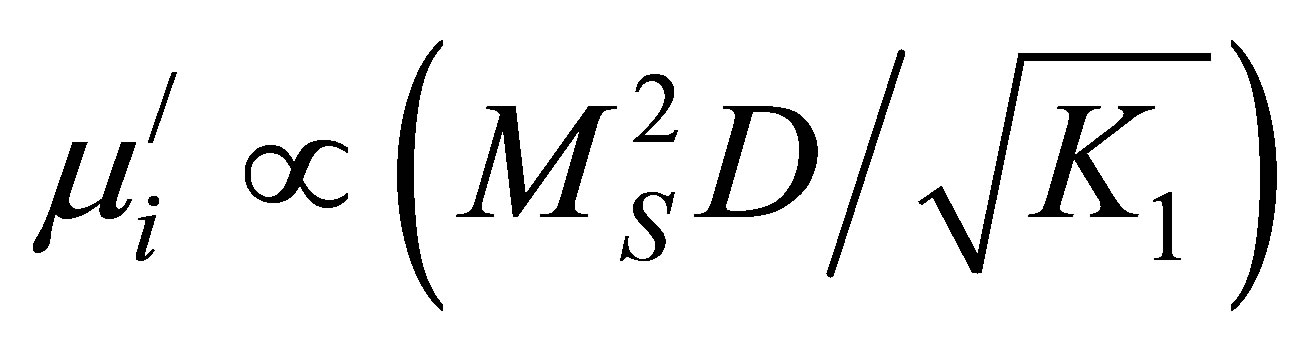 , where Ms is the saturation magnetization; K1 is the anisotropy constant [22]. In our present study of microstructure, it is seen that the D increases significantly with Cu2+ content. Therefore, the increase of
, where Ms is the saturation magnetization; K1 is the anisotropy constant [22]. In our present study of microstructure, it is seen that the D increases significantly with Cu2+ content. Therefore, the increase of 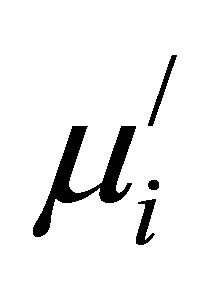 with increasing Cu2+ content is justified. The increasing
with increasing Cu2+ content is justified. The increasing 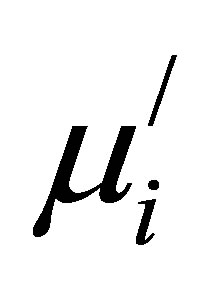 with Ts is due to increase in both
with Ts is due to increase in both 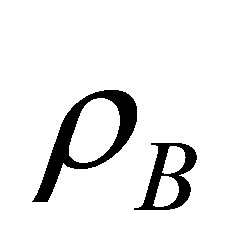 and D.
and D.
Figure 8 shows the variation of 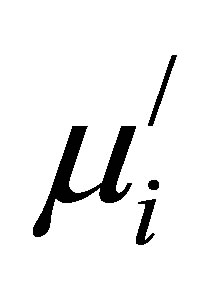 with Cu2+ content at different frequencies for various Mn0.50-xZn0.50CuxFe2O4 sintered at 1200˚C, 1250˚C and 1300˚C. It is found that
with Cu2+ content at different frequencies for various Mn0.50-xZn0.50CuxFe2O4 sintered at 1200˚C, 1250˚C and 1300˚C. It is found that 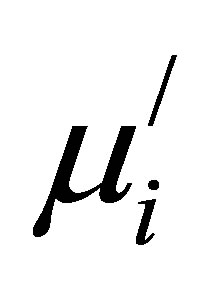 decreases at higher frequencies. This is due to the fact that at higher frequencies impurities between grains and intragranular pores act as pinning points and increasingly hinder the motion of spin and domain walls thereby decreasing their contribution to permeability and also increasing the loss [22].
decreases at higher frequencies. This is due to the fact that at higher frequencies impurities between grains and intragranular pores act as pinning points and increasingly hinder the motion of spin and domain walls thereby decreasing their contribution to permeability and also increasing the loss [22].
For practical application the quality factor is often used as a measure of performance. The RQF increases with an increase of frequency, showing a peak and then decreases with further increase in frequency as shown in Figure 9. The variation of RQF with frequency showed a similar trend for all the samples. It is observed that the sample sintered at 1250˚C has the highest RQF (5420) for Mn0.40Zn0.50Cu0.10Fe2O4. The highest RQF for Mn0.20Zn0.50Cu0.30Fe2O4 is 5420 sintered at 1250˚C. This is probably due to the growth of less imperfection and defects compared to those of other samples [9].
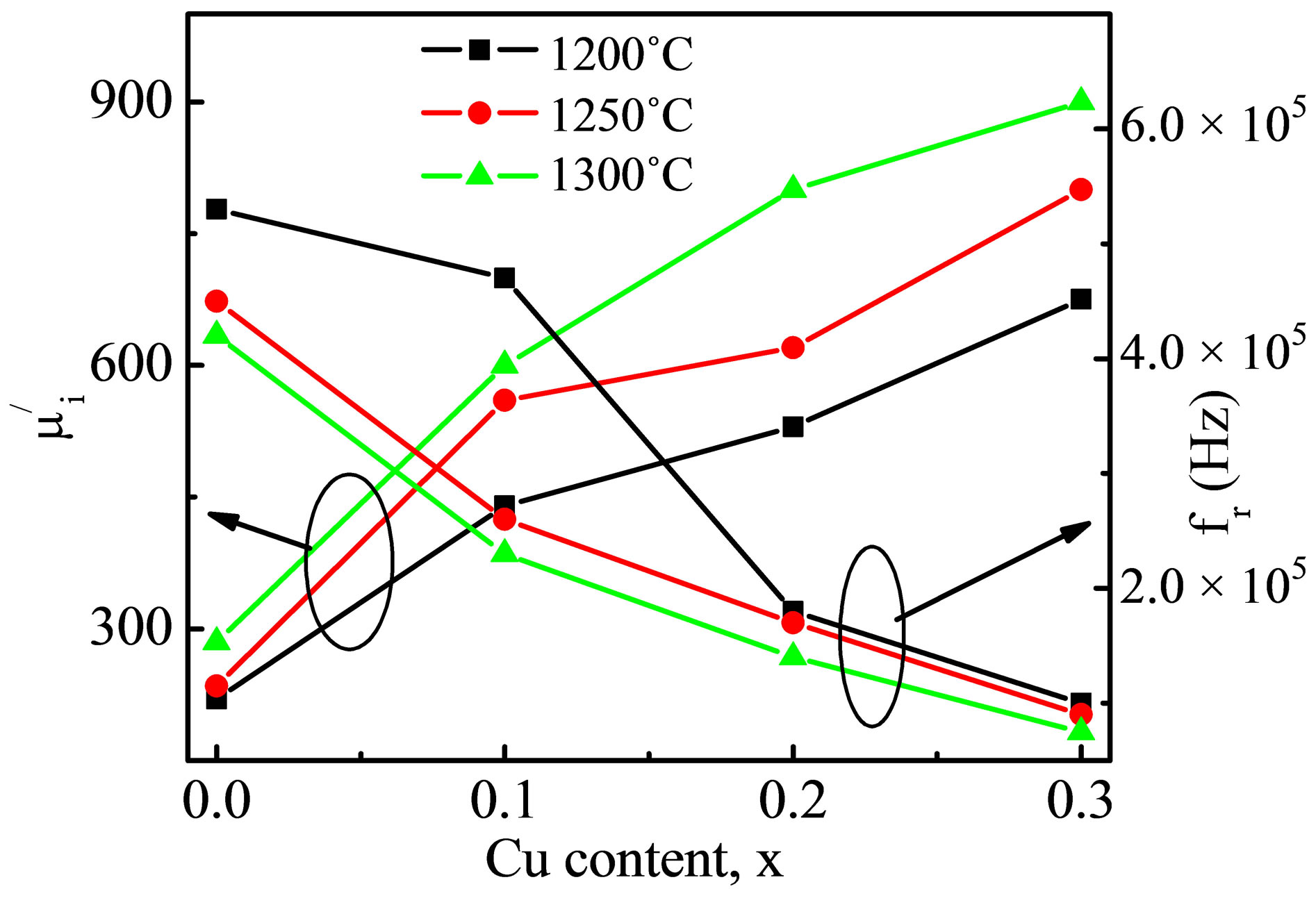
Figure 7. The variation of initial permeability and resonance frequency of Mn0.50-xZn0.50CuxFe2O4 at different Ts.
 (a)
(a) (b)
(b)
Figure 8. The initial permeability of Mn0.50-xZn0.50CuxFe2O4 with Cu2+ content at different frequencies sintered at (a) 1200˚C, (b) 1250˚C and (c) 1300˚C.
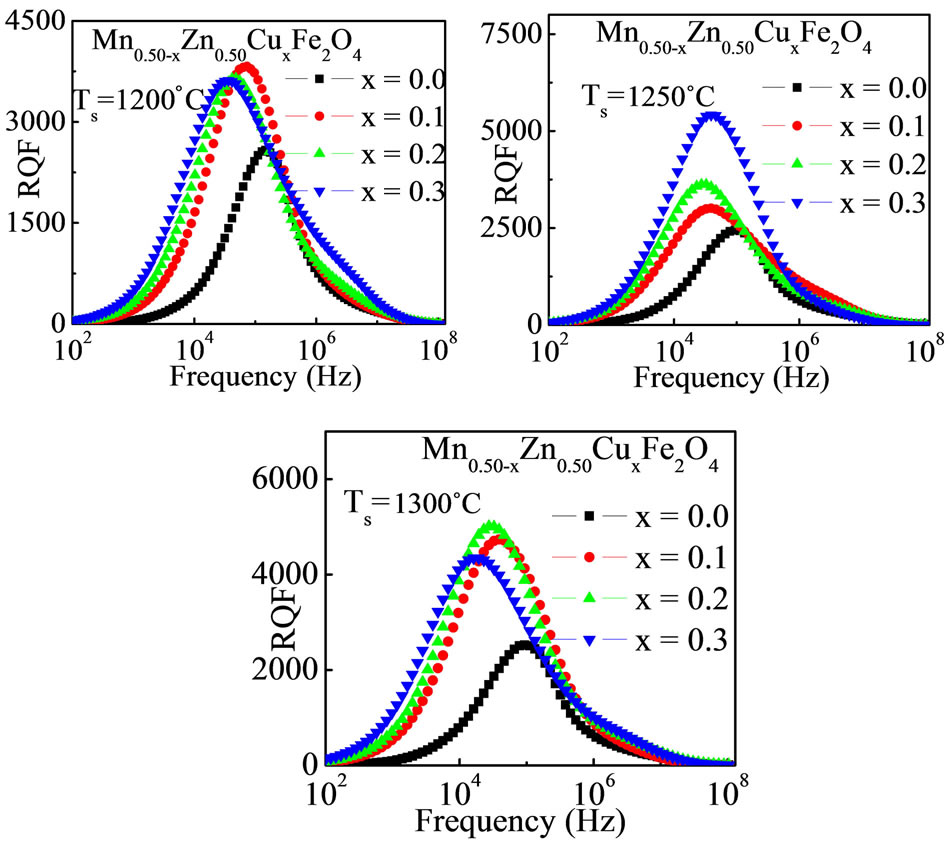
Figure 9. The RQF of Mn0.50-xZn0.50CuxFe2O4 with Cu2+ content sintered at 1200˚C, 1250˚C and 1300˚C.
3.3.2. Temperature Dependent Permeability
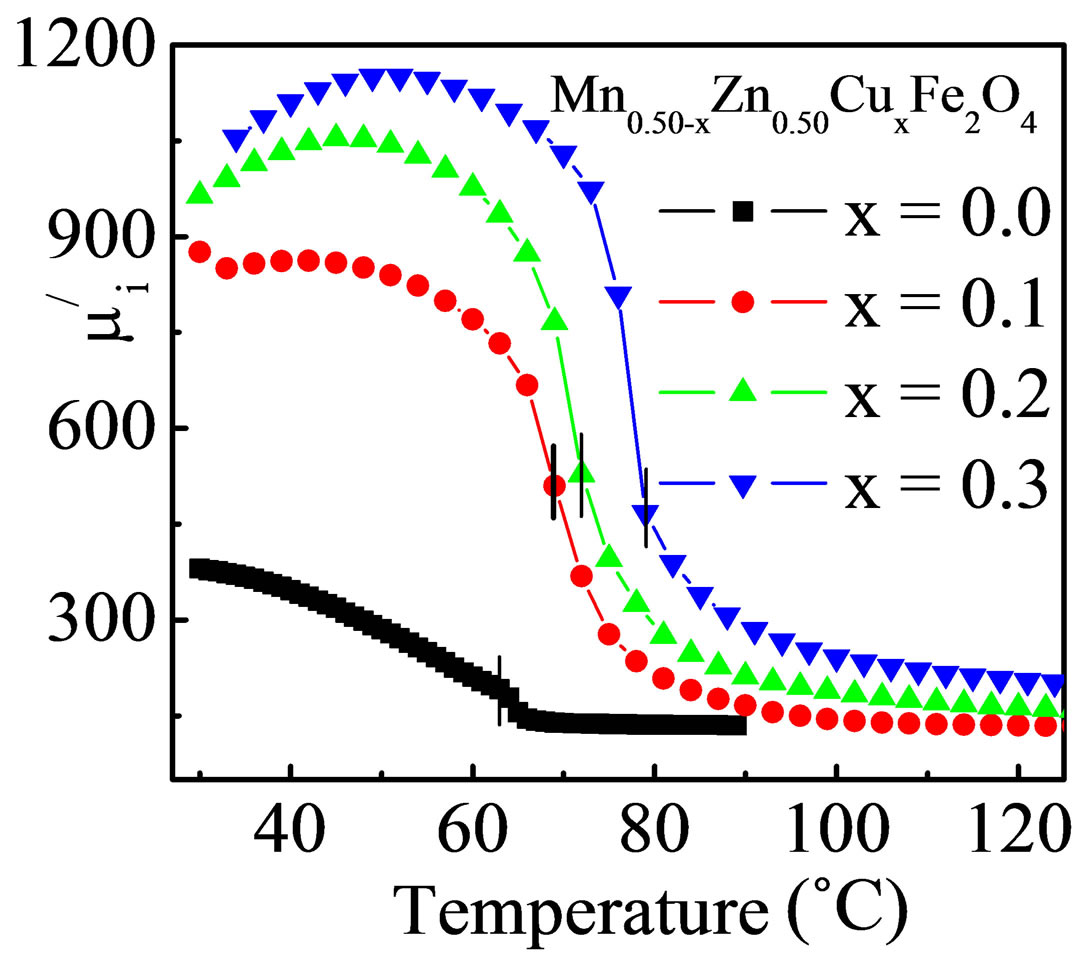
The 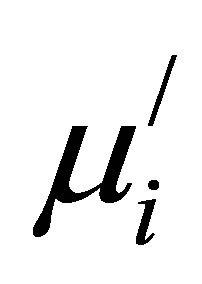 as a function of temperature for various Mn0.50-xZn0.50CuxFe2O4 sintered at 1200˚C is shown in Figure 10(a).
as a function of temperature for various Mn0.50-xZn0.50CuxFe2O4 sintered at 1200˚C is shown in Figure 10(a).
It is observed that there is a sudden drop in  at Néel temperature, TN, where the magnetic state of the ferrite changes from ferrimagnetic to paramagnetic state. This is because at TN, the thermal agitation is so high that it reduces the alignment of the magnetic moment along a given axis to zero [29]. Figure 10(b) shows the variation of TN with Cu2+ content. It is observed that TN increases
at Néel temperature, TN, where the magnetic state of the ferrite changes from ferrimagnetic to paramagnetic state. This is because at TN, the thermal agitation is so high that it reduces the alignment of the magnetic moment along a given axis to zero [29]. Figure 10(b) shows the variation of TN with Cu2+ content. It is observed that TN increases
 (a)
(a) (b)
(b)
Figure 10. (a) The temperature dependent initial permeability and (b) Néel temperature of Mn0.50-xZn0.50CuxFe2O4 with Cu2+ content sintered at 1200˚C.
With increase in Cu2+ substitution for Mn2+ in Mn0.50-xZn0.50CuxFe2O4 due to strengthening of A-B interaction between the two sublattices. This could be attributed to the decrease in distance (hooping length) between the magnetic ions of Aand B-sites and is confirmed by the decrease in the lattice parameter with increase in Cu2+ content as shown in Figure 2. The shorter distance between magnetic cations leads to the increase in A-B interaction and consequently TN increases.
3.3.3. B-H Loops of Mn0.50-xZn0.50CuxFe2O4
Figure 11(a) shows the B-H loops of Mn0.50-xZn0.50CuxFe2O4 sintered at 1200˚C at constant frequency 1000 Hz and Figure 11(b) is the B-H loops for low field.
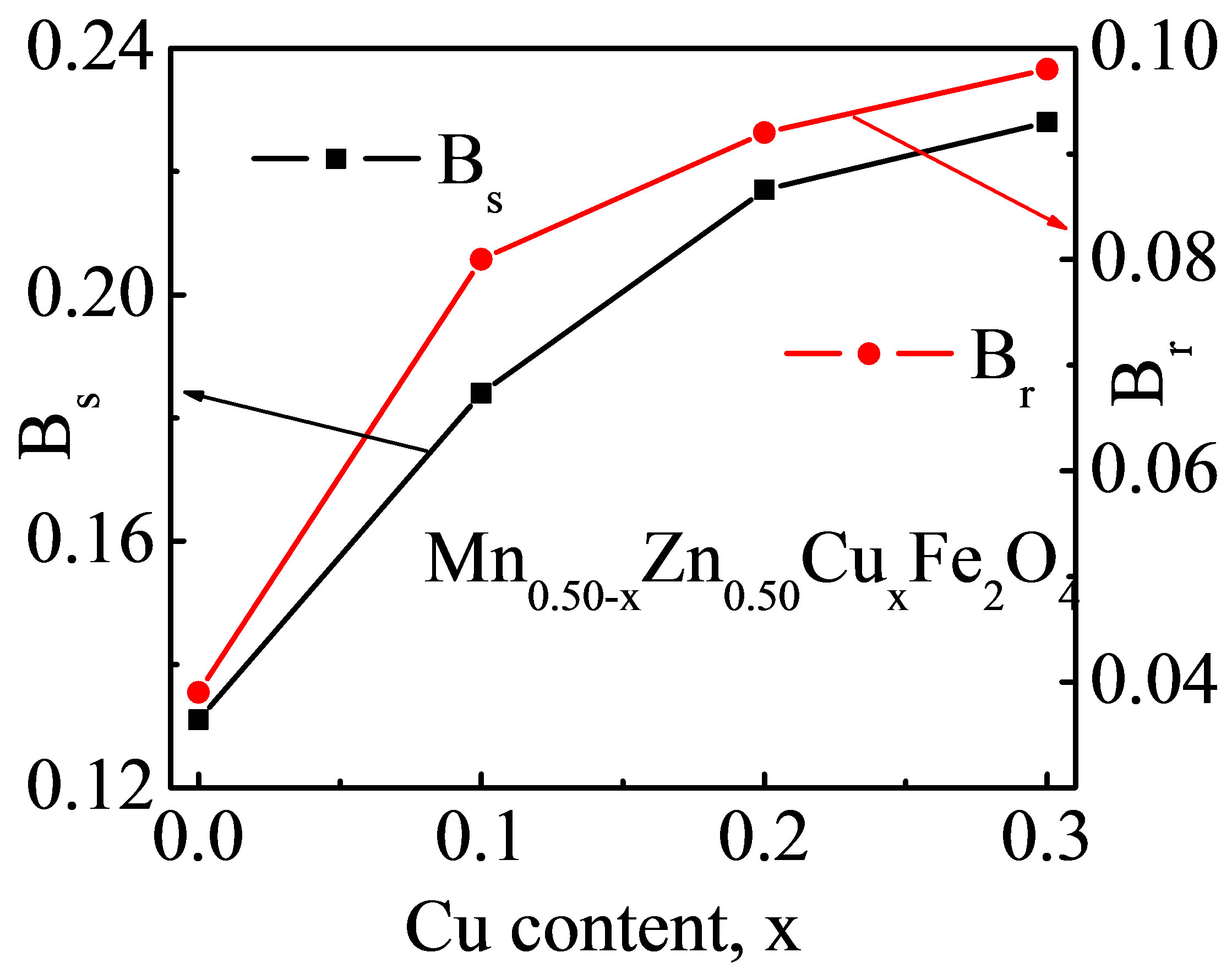
The magnetic induction, B of all samples increases linearly with increase in applied magnetic field up to 120 A/m (depending on compositions). Beyond 120 A/m, B increases slowly and then reaches to the saturation induction, Bs. Increasing B with applied low field H indicates that all compositions are in ferromagnetic state at room temperature. From the loops Bs has been calculated. It is observed that Bs increases with increasing Cu2+ content which is shown in Figure 12(a).
The variation in saturation magnetization with Cu2+ content could be explained by cation distribution and exchange interaction. It is well known that Zn2+ ion has strong A-site occupancy, Mn2+ ions prefer to go both sites (80% Aand 20% B-sites) [16]. Also Cu2+ and Fe3+ ions can occupy both Aand B-sites. Substitution of Cu2+ in place of Mn2+ results into migration of some of Fe3+ from Ato B-site. The change in Br (residual induction) and Bs with Cu2+ content are shown in Figure 12(b). The coercive field (Hc) for each sample has been measured from the B-H loops of Mn0.50-xZn0.50CuxFe2O4 which is shown in Figure 12(b). It is observed that Hc decreases
 (a)
(a)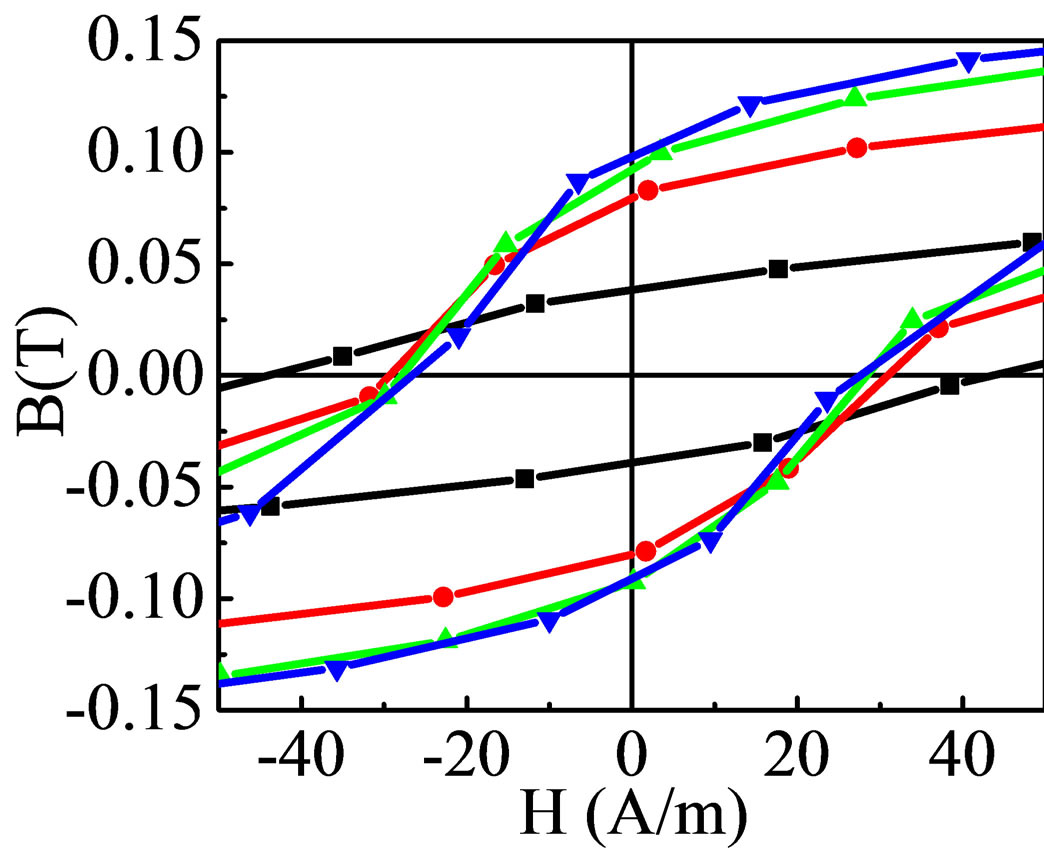 (b)
(b)
Figure 11. (a) B-H loops of Mn0.50-xZn0.50CuxFe2O4 (b) B-H loops at low field sintered at 1200˚C.
 (a)
(a)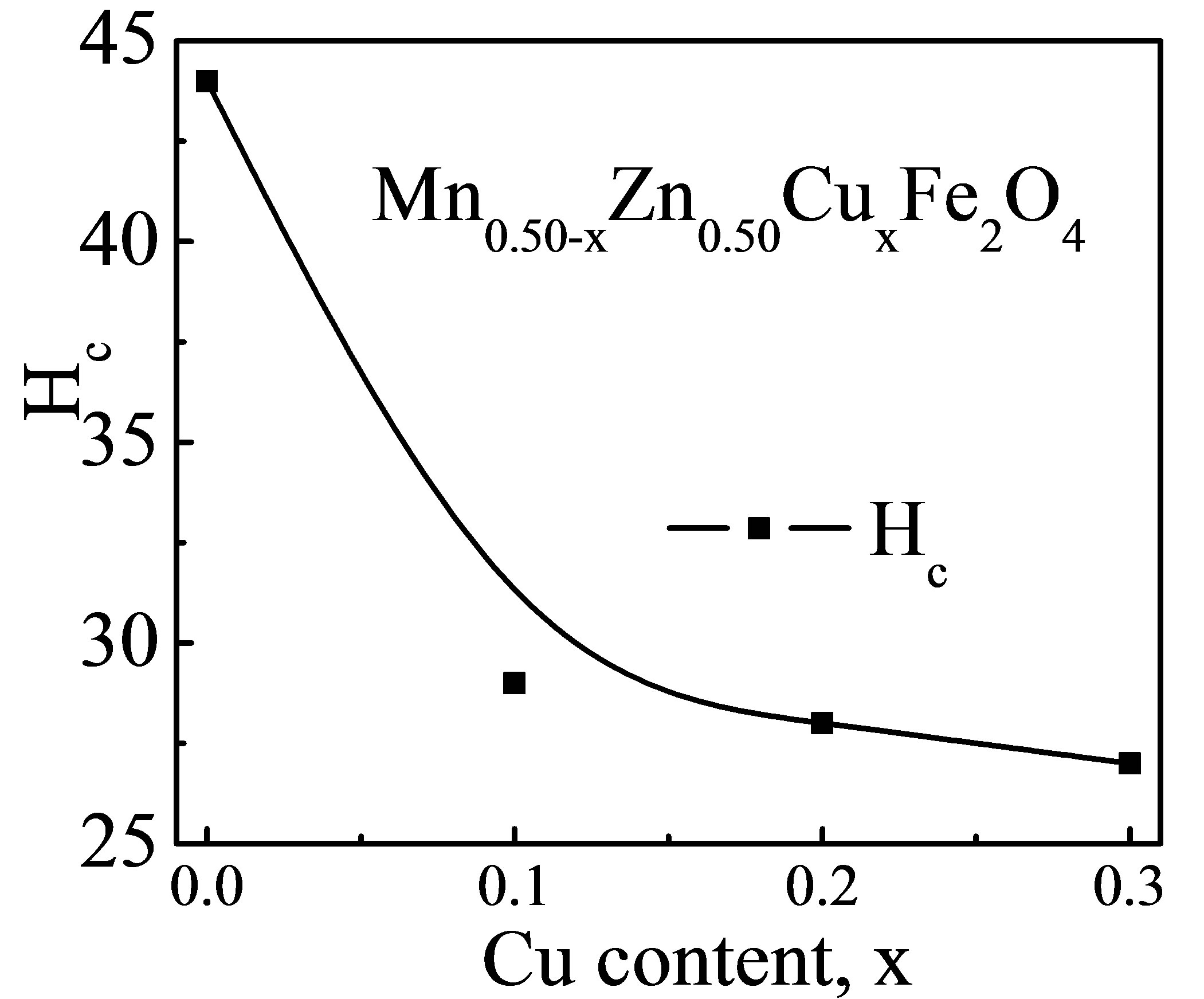 (b)
(b)
Figure 12. (a) The Bs and Br and (b) Coercive field of Mn0.50-xZn0.50CuxFe2O4 with Cu2+ content sintered at 1200˚C.
with increase in Cu2+ content, whereas 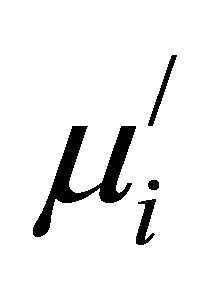 increases. Mazen and Abu-Elsaad reported that Hc is directed to gradually decreasing with D [29]. Our experimental result is in agreement with the reported value. Therefore, samples having larger grains are expected to have lower Hc.
increases. Mazen and Abu-Elsaad reported that Hc is directed to gradually decreasing with D [29]. Our experimental result is in agreement with the reported value. Therefore, samples having larger grains are expected to have lower Hc.
4. Conclusion
Substitution of Cu2+ causes appreciable change in the structural and magnetic properties of the Mn-Cu-Zn ferrites. The XRD patterns confirm single phase cubic spinel structure of Mn0.50-xZn0.50CuxFe2O4. The a0 decreases with the increase in Cu2+ content while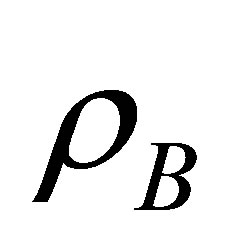 , D,
, D, 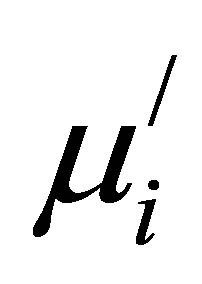 and TN increase with the increase in Cu2+. The Hc decreases with the increase in Cu2+ content.
and TN increase with the increase in Cu2+. The Hc decreases with the increase in Cu2+ content. 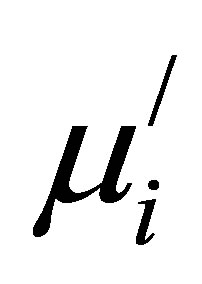 is greatly enhanced from 258 to 1061 (~400%). The highest RQF (5420) has been found for the sample Mn0.20Zn0.50Cu0.30Fe2O4 sintered at 1250˚C. These ferrites are important and suitable for technological applications because of their high permeability.
is greatly enhanced from 258 to 1061 (~400%). The highest RQF (5420) has been found for the sample Mn0.20Zn0.50Cu0.30Fe2O4 sintered at 1250˚C. These ferrites are important and suitable for technological applications because of their high permeability.
REFERENCES
- K. Praveena, K. Sadhana, S. Bharadwaj and S. R. Murthy, “Developement of Nanocrystalline Mn-Zn Ferrites for High Frequency Transformer Applications,” Journal of Magnetism and Magnetic Materials, Vol. 321, 2009, pp. 2433-2437. http://dx.doi.org/10.1016/j.jmmm.2009.02.138
- P. Mathur, A. Thakur and M. Singh, “Low Temperature Synthesis of Mn0.4Zn0.6In0.5Fe1.5O4 Nano Ferrite for HighFrequency Applications,” Journal of Physics and Chemistry of Solids, Vol. 69, No. 1, 2008, pp. 187-192. http://dx.doi.org/10.1016/j.jpcs.2007.08.014
- J. Kalarus, G. Kogias, D. Holz and V. T. Zaspalis, “High Permeability-High Frequency Stable MnZn Ferrites”, Journal of Magnetism and Magnetic Materials, Vol. 324, No. 18, 2012, pp. 2788-2794. http://dx.doi.org/10.1016/j.jmmm.2012.04.011
- A. Goldman, “Modern Ferrite Technology,” Van Nostrand Reinhold, New York, 1990.
- Amarendra K. Singh, Abhishek K. Singh, T. C. Goel and R. G. Mendiratta, “High Performance Ni-Substituted MnZn Ferrites Processed by Soft Chemical Technique”, Journal of Magnetism and Magnetic Materials, Vol. 281, No. 2-3, 2004, pp. 276-280. http://dx.doi.org/10.1016/j.jmmm.2004.04.115
- H. Su, H. W. Zhang, X. L. Tang and X. Y. Xiang, “HighPermeability and High-Temperature NiCuZn Ferrite”, Journal of Magnetism and Magnetic Materials, Vol. 283, No. 2-3, 2004, pp. 157-163. http://dx.doi.org/10.1016/j.jmmm.2004.05.017
- M. Manjurul Haque, M. Huq and M. A. Hakim, “Influence of CuO and Sintering Temperature on the Microstructure and Magnetic Properties of Mg-Cu-Zn Ferrites,” Journal of Magnetism and Magnetic Materials, Vol. 320, No. 21, 2008, pp. 2792-2799. http://dx.doi.org/10.1016/j.jmmm.2008.06.017
- M. H. R. Khan and A. K. M. Akther Hossain, “Reentrant Spin Glass Behavior and Large Initial Permeability of Co0.5-xMnxZn0.5Fe2O4,” Journal of Magnetism and Magnetic Materials, Vol. 324, No. 4, 2012, pp. 550-558. http://dx.doi.org/10.1016/j.jmmm.2011.08.039
- A. K. M. Akther Hossain and M. L. Rahman, “Enhancement of Microstructure and Initial Permeability Due to Cu Substitution in Ni0.50-xCuxZn0.50Fe2O4 Ferrites,” Journal of Magnetism and Magnetic Materials, Vol. 323, No. 15, 2011, pp. 1954-1962. http://dx.doi.org/10.1016/j.jmmm.2011.02.031
- J. B. Nelson and D. P. Riley, “An Experimental Investigation of Extrapolation Methods in the Dimensions of Accurate Unit-Cell,” Cambridge, 1944.
- L. Vegard, “The Constitution of Mixed Crystals and the Space Occupied by Atoms,” Zeitscchrift fur Physik, Vol. 5, No. 17, 1921, pp. 17-26.
- R. D. Shanon and C. T. Prewitt, “Effective Ionic Radii in Oxides and Fluorides,” Acta Crystallographica, Vol. 25, No. B, 1969, pp. 925-946.
- V. G. Patil, Sagar E. Shirsath, S. D. More, S. J. Shukla and K. M. Jadhav, “Effect of Zinc Substitution on Structural and Elastic Properties of Cobalt Ferrites,” Journal of Alloys and Compounds, Vol. 488, No. 1, 2009, pp. 199- 203. http://dx.doi.org/10.1016/j.jallcom.2009.08.078
- D. Ravinder, L. Balachander and Y. C. Venudhar, “Electrical Conductivity in Manganese Substituted Lithium Ferrites,” Materials Letters, Vol. 49, No. 5, 2001, pp. 267-271. http://dx.doi.org/10.1016/S0167-577X(00)00381-5
- D. R. Lide, “CRC Handbook of Chemistry and Physics,” 76th Edition, CRC Press, Boca Raton, 1995.
- S. E. Shirsath, B. G. Toksha, R. H. Kadam, S. M. Patage, D. R. Mane, G. S. Jangam and A. Ghashemi, “Doping Effect of Mn2+on the Magnetic Behavior in Ni-Zn Ferrite Nanoparticles Prepared by Sol-Gel Auto-Combustion,” Journal of Physics and Chemistry of Solids, Vol. 71, No. 12, 2010, pp. 1669-1675. http://dx.doi.org/10.1016/j.jpcs.2010.08.016
- M. Manjurul Haque, M. Huq and M. A. Hakim, “Densification, Magnetic and Dielectric Behavior of Cu-Substituted Mg-Zn Ferrites,” Materials Chemistry and Physics, Vol. 112, No. 2, 2008, pp. 580-586. http://dx.doi.org/10.1016/j.matchemphys.2008.05.097
- S. R. Murthy, “A Study of Ultrasonic Velocity and Attenuation on Polycrystalline Ni-Zn Ferrites,” Bulletin of Material Science, Vol. 24, No. 6, 2001, pp. 611-616. http://dx.doi.org/10.1007/BF02704009
- K. O. Low and F. R. Sale, “Electromagnetic Properties of Gel-Derived NiCuZn Ferrites,” Journal of Magnetism and Magnetic Materials, Vol. 246, No. 1-2, 2002, pp. 30- 35. http://dx.doi.org/10.1016/S0304-8853(01)01390-7
- M. I. Mendelson, “Average Grain Size in Polycrystalline Ceramics,” Journal of American Ceramic Society, Vol. 52, No. 8, 1969, pp. 443-446. http://dx.doi.org/10.1111/j.1151-2916.1969.tb11975.x
- J. L. Snoek, “Dispersion and Absorption in Magnetic Ferrites at Frequencies above One Mc/s,” Physica, Vol. 14, No. 4, 1948, pp. 207-217. http://dx.doi.org/10.1016/0031-8914(48)90038-X
- A. Globus, P. Duplex and M. Guyot, “Determination of Initial Magnetization Curve from Crystallites Size and Effective Anisotropy Field,” IEEE Transactions Magazine, Vol. 7, No. 3, 1971, pp. 617-622. http://dx.doi.org/10.1109/TMAG.1971.1067200
- T. Nakamura, “Low Temperature Sintering of Ni-Zn-Cu Ferrite and Its Permeability Spectra,” Journal of Magnetism and Magnetic Materials, Vol. 168, 1997, pp. 285-291. http://dx.doi.org/10.1016/S0304-8853(96)00709-3
- J. Smit and H. P. J. Wijn, “Ferrites,” Philips’ Technical Library, 1959.
- J. Hu and M. Yan, “Preparation of High-Permeability NiCuZn Ferrite,” Journal of Zhejiang University Science B, Vol. 6, No. 6, 2005, pp. 580-583.
- T. Tsutaoka, M. Ueshima, T. Tokunaga, T. Nakamura and K. Hatakeyama, “Frequency Dispersion and Temperature Variation of Complex Permeability of Ni-Zn Ferrite Composite Materials,” Journal of Applied Physics, Vol. 78, No. 6, 1995, pp. 3983-3991. http://dx.doi.org/10.1063/1.359919
- E. P. Wohlfarth, “Ferromagnetic Materials: A Handbook on the Properties of Magnetically Ordered Substances,” Elsevier Science, 1980.
- S. V. Kakatkar, S. S. Kakatkar, R. S. Patil, A. M. Sankpal, N. D. Chaudhari, P. K. Maskar, S. S. Suryawanshi and S. R. Sawant, “Effect of Sintering Conditions and Al3+ Addition on Wall Permeability in Ni1-xZnxAltFe2-tO4 Ferrites,” Materials Chemistry and Physics, Vol. 46, 1996, pp. 96-99. http://dx.doi.org/10.1016/0254-0584(96)01746-4
- S. A. Mazen and N. I. Abu-Elsaad, “Structural and Some Magnetic Properties of Manganese-Substituted Lithium Ferrites,” Journal of Magnetism and Magnetic Materials, Vol. 324, No. 20, 2012, pp. 3366-3373. http://dx.doi.org/10.1016/j.jmmm.2012.05.056
NOTES
* Corresponding author.

