ABSTRACT

We use a dual Einstein-Kaluza spacetime to calculate the exact energy density of dark energy and dark matter using a novel topological computation me- thod. Starting from the said spacetime and ‘tHooft’s topological renormalon as well as the corresponding symmetry group, we show how the zero set quan- tum particle and the empty set quantum wave interact with the vacuum and give rise to pure dark energy and pure dark matter all along with ordinary energy density of the cosmos. The consistency of the exact calculation and the accurate observations attests to the reality of ‘tHooft’s renormalon dark matter, pure dark energy and accelerated cosmic expansion.

Keywords:

Accelerated Cosmic Expansion, tHooft Renormalon, Cantorian Spacetime, Dark Matter, Pure Dark Energy, Topological E-Infinity Computation, Zero Set Quantum Particle, Empty Set Quantum Wave, Hausdorff Mass of Ordinary Energy, Topological Mass of Dark Energy, Mixed Mass of Dark Matter and Pure Dark Energy, A Dual Einstein-Kaluza Spacetime

1. Introduction and Motivation

Let us stand by outlining the motivation and background leading to the present paper using the mathematical principles of E-infinity Cantorian fractal spacetime theory [1] - [6] ; ‘tHooft’s dimensional regularization method [7] - [12] was developed to the point where it could be used to determine the exact density of dark energy and ordinary energy of the cosmos [13] - [28] . In the course of doing that the unique role of a hypothetical particle dubbed ‘tHooft renormalon [8] [10] [11] [12] was uncovered and its profound role in simplifying intricate computation in high energy physics and cosmology was made plausible [21] [24] [25] [26] [27] [28] .

The present work goes much further in the above direction and formalizes the handling of what may be called the renormalon topological computation machinery [12] [20] to the extent of determining not only the exact density of ordinary measurable energy and the exact dark energy which cannot be measured directly [13] - [21] but also to the point that we were able to distinguish between the pure dark energy and pure dark matter energy density as well as their mutual coupling [2] and the coupling to the compactified holographic boundary of our universe. Our starting points are as usual A. Connes’ dimensional function of Penrose fractal tiling universe [16] and the associated zero set quantum particle given by the bi-dimensions 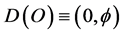and the empty set quantum wave given by 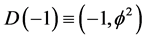where 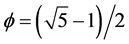[13] [18] . We assume furthermore familiarity with the ‘tHooft E-infinity renormalon as well as its connection with Hardy’s quantum entanglement and Hardy’s entangleon 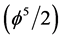and its connection to Einstein’s maximal energy density 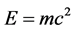where c is the velocity of the light [17] [20] . In addition we will be making extensive use of the procedure of compactifying the SL(2, 7) Lie symmetry group of the holographic boundary [15] [16] using 64 entangleons leading to an effective dimension equal to 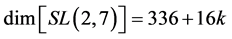[15] [16] . In particular, it will be demonstrated that the inverse of this dimension is the relevant coupling between the pure dark energy density and the corresponding density of dark matter’s energy [21] . The consistency of exact analysis and high accurate cosmic observations and measurements attests to the reality of our entire scenario. Last but by no means not least a new way of looking at a dual Einstein-Kaluza spacetime will lead to undreamed of simple solution of the dark matter and Dark Energy problem.

2. Formalizing Topological Renormalon Computation

Let us go directly to the formal handling of the renormalon topological computation without much ado. From von Neumann-Connes’ dimensional function, E-infinity postulates that a pre-quantum particle may be identified by the zero set 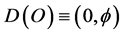while its cobordism, namely the empty set models the pre- quantum wave given by 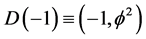[13] [21] . Furthermore, the topological dimension of the maximal volume unit sphere, namely D = 5 is identified with Kaluza-Klein’s topological dimension of the universe and at the same time it represents the topological mass charge of the particle giving rise to dark energy from acting on the empty set vacuum [19] . On the other hand the Hausdorff mass charge which gives rise to measurable ordinary energy is the inverse of the fractal-Hausdorff dimension of Einstein’s spacetime which means 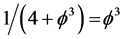[1] [17] . In addition to the topological mass charge and the Hausdorff mass charge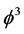, the new mass charge which we introduce here is a mixture of the Hausdorff dimension of the empty set, i.e. 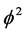and the classical 3D of ordinary Newtonian mass. In other words letting the empty set 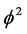act on 3D mass we find 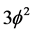of dark matter mass charge which is almost Newtonian but with a fractal Hausdorff flavour [21] . Thus while for ordinary energy we have 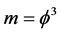and for dark energy we have m = 5, for dark matter we have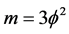. The three different topological energy densities may be found from the classical kinetic energy of Newtonian mechanics in our usual manner [13] [2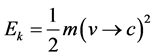1]

(1)

to be [19] [20] [21]

(2)

for ordinary energy density 4.5% and

(3)

for dark energy density. Finally for pure dark matter we have

(4)

all in excellent agreement with cosmic measurements [12] - [17] . After this short overview we turn our attention to the exact calculation of all the relevant energy densities of the cosmos as well as the virtual determination of the pure dark energy density which is the cause behind the accelerated cosmic expansion [14] [15] .

3. The Three Fundamental Energy Densities of the Cosmos

The E-infinity hierarchy [1] takes the hierarchy of transfinite set theory as well as the principle of self similarity literally and applies it to our cosmos [14] - [21] . Thus we start with the zero set ad find that its cobordism is the empty set [19] and in turn the emptier set is the cobordism of the empty set [19] . Translating to physics we postulate that the zero set is the pre-quantum particle given by zero and [17] . The surface of this particle is the guiding or ghost pre-quantum wave given by minus one and [17] . Finally the surface of the pre-quantum wave is an emptier set constituting the beginning of spacetime which is a Russian doll concentric empty set with increasing degrees of emptiness [1] [17] [21] , i.e. then, and so on until we have which is the true unsubstantial nothingness [1] [21] . Consequently we have three fundamental types of energy density in our cosmos which is essentially a super large black hole pre-quantum particle surrounded by a world pre-quantum wave surrounded by a pre-spacetime which is embedded into a multi-fractal of empty sets with increasing degrees of emptiness [1] [20] [21] . Now guided by Einstein’s famous where gives us an opportune interpretation of Einstein’s formula not only as a conversion equation of mass into energy but as the maximal energy density possible in the universe [21] , then we can write our three fundamental energy densities as follows:

1) for ordinary energy we have

(5)

2) for dark energy we have

(6)

Now completing the to pologizing physics program of E-infinity, it was reasoned in numerous previous publications that the topological speed of light is equal and consequently we have [13] [21]

(a):

(7)

for the ordinary energy density and

(b):

(8)

for the dark energy density of the universe where is the Hausdorff mass of the zero set quantum particle and 5 is the topological mass of the empty set quantum wave [13] [20] .

This result was of course noted long ago to be in astounding agreement with all modern measurements and cosmic observations [14] - [21] . Before moving to the case (c), namely that of dark matter energy density and its coupled partner D, namely the pure dark energy density, we would like to rephrase mathematically our alternative interpretations of cases (a) and (b).

Remembering that the zero set is given by 0 and and that it is a five dimensional zero set, it is clear that the energy density in this case can be interpreted as a topological multiplicative volume, namely and that is in full agreement with what we have shown here via the kinetic energy [20] . For the dark energy density on the other hand, i.e. in the case of an additive process, the topological volume is an additive five dimensional empty set which means [14] - [21] . Adding both “volumes” one finds Einstein’s formula from the kinetic energy formula by noting that [13] - [20]

(9)

This alone should dispel any lurking doubt about our method. Now we can return to our main task, namely case (c) of dark matter density. This is consequently given in the uncoupled approximation by [4] [21]

(c):

(10)

Consequently the pure dark energy must be [14] - [21] . More explicitly pure dark energy in the uncoupled approximation is connected to ‘tHooft’s fractal spacetime and may be written as

(d):

(11)

where k is the ‘tHooft renormalon given by and is the entangleton charge of Hardy’s quantum entanglement. Compared to all other results, the last one is not as accurate as all the previous ones because ignoring the coupling between and on the one hand and the coupling of both with the holographic boundary has this adverse effect [15] [16] . We look at this subtle point in the next section.

4. Exact Determination of the Coupled Dark Matter Energy Density and Pure Dark Energy Density with Regard to the Role of ‘tHooft’s Renormalon

As mentioned in the introduction, the model we are using here for the entire universe is that of ‘tHooft’s holographic boundary [7] [8] [9] [15] [16] . In turn this is taken to be a Penrose-like tiling universe which is nearly indistinguishable from a compactified Kleinian modular curve with 336 degrees of freedom [15] [16] . Interpreting these 336 as SL(2, 7) isometries we may “compactify” the “crisp” SL(2, 7) and find the transfinitely correct number of isometries to be [1] [15] [16]

(12)

Seen that way we can say the share of each unit particle-like state of the overall effect of the holographic boundary is the inverse of. It turns out that this inverse value is the coupling between the pure dark energy and the dark matter energy density sector. In fact some would feel that plays the role of mass splitting or mass gap but this will not be discussed here. The fact that pure dark energy has an opposite sign to that of dark matter may be manifestly seen from how enters into the equation. For dark matter is added to the attractive force while for pure dark energy it is subtracted. Taking all these points into consideration, we can write the following [4] [21] :

1) The exact coupled expression for the attractive dark matter energy is

(13)

exactly as found using entirely different methods [14] [21] .

2) For the exact repulsive pure dark energy on the other hand one finds

(14)

Again this agrees exactly with our previous exact analysis using Heterotic string theory in conjunction with a fuzzy Kähler manifold [14] [20] [21] .

5. The Dual Einstein-Kaluza Spacetime and the Threefold Nature of Energy

It is fair to say that most if not all physicists think that D = 4 Einstein spacetime and D = 5 Kaluza spacetime are two alternatives of which one has to be chosen depending on what we want to determine and understand. In that respect the present Author was until quite recently no exception. However, it has dawned on us that our fractal version of Kaluza-Klein theory with as was extensively discussed for instance in Ref. [17] , is in fact a unification of both D = 4 of Einstein and D = 5 of Kaluza. Simple calculation reveals in the most obvious manner that our real spacetime is a 5-dimensional smooth manifold from the outside resembling a watermelon but of a higher dimension. From the inside however it is as fractal as a watermelon as well with a fractal dimension equal to [24] [25] [26] [27] [28] .

(15)

Consequently the total dimension is of course not 5 + 4 = 9 but rather. Now the beauty of it all is that represents the ordinary energy part because is the representative of a zero set quantum particle. By contrast the 5 is the topological 5-dimensional manifold as corresponding to the empty set quantum wave. We can thus call the Hausdorff mass and call 5 the Topological mass so that the total mass is. Taking the classical formula of the kinetic energy and noting that and the total energy becomes. Restoring natural units we see that and that E should be written as. From the above it is clear that [4] [13]

(16)

where E(D) is the total energy density of the dark sector and E(O) is the ordinary energy density. Now we can dissect E(D) into its two components namely dark matter and pure dark energy. It is here that we discover the beauty of D = E(Einstein) + 1 = D(Kaluza) = 5 and the reality of ‘tHooft’s renormalon k [7] - [12] . This is because we can write

(17)

From the last expansion we see that our ordinary energy density is the exact one namely [24] [25] [26] [27] [28]

(18)

in full agreement with all previous results and measurements [10] - [21] . On the other hand dark matter is due to fractal strings made of classical D = 1 string. In addition to one attached namely ‘tHooft’s renormalon, namely [7] - [12]

(19)

This leads to a density of

(20)

which is extremely close to the exact value of 22.18033% [7] - [12] [10] - [21] . For the pure dark energy density on the other hand, one finds a ratio of ‘tHooft’s fractal spacetime and the combined Einstein-Kaluza spacetime which gives us [10] - [21]

(21)

Again this is an excellent approximation to the exact value 0.733111 [7] - [12] [10] - [21] .

It is by now obvious to the reader that we did not obtain the exact value of the Dark matter energy density only because we ignored it unlike ordinary energy this two subdivision of the energy are weakly coupled. The coupling constant in this case is which is a mass-splitting or a mass gap-like factor which must be divided by the fractal Einstein space dimension namely. Thus this coupling is given by [4] [22] . Including in the previous approximate expression, one finds for dark matter

(22)

which is the exact value. For pure dark energy on the other hand, one finds [24] [25] [26] [27] [28]

(23)

which is again the exact value obtained in the present paper using different methods. The advantage of using the novel dual Einstein-Kaluza spacetime formulation is a definite deeper insight and understanding of the various components of energy and the role of ‘tHooft’s quasi particle which we accept it to be a real elementary particle [7] - [12] which in due time will be found experimentally in the Laboratory of high energy physics and cosmology [1] - [28] .

6. Discussion and Conclusions

To have a chance to answer deep questions about the very nature of physical existence and probe troubling questions about the nature of physics, we need equally deep and sometimes illusively abstract mathematical tools and philosophical notions and concepts. In particular deep mathematics, it is both very simple and equally very hard to come by and to comprehend because it is remote from our mundane classical world in which we are born, cared for and nourished long before we can utter a single intelligible word as infants let alone thinking of ourselves as infallible geniuses.

In the present work, one of the simplest tools used may be the hardest to understand, namely setting the speed of light to be a constant equal [20] [21] and despite of that it finds answers to our questions using which is consistent not only with logic but also with sophisticated as well as fundamental theorem such as KAM as well as real experiments [1] [17] . In the circumstances one is excused to ask how this is possible. A tentative answer to this impossible question may be as follows:

Let us recall that we have decided to start building our universe from scratch and began with the obvious, namely spacetime just as Einstein started for instance [1] - [6] . Then we decided to build this spacetime from Cantor dust beginning with a one dimensional Cantor set [1] [17] . Such a set has no topological dimensions because it is zero dimensional fractal points which form this set [15] - [21] . Worse still, this Cantor set has no extension what so ever being measure zero according to measure theory and common sense alike [15] - [21] . How could we under such circumstances define the speed of an esoteric car crossing this esoteric one dimensional Cantor universe? Everything we could have is zero so it is not really zero, is it? Yes but wait a minute, a naive voice could tell us all this is because the set has something else not that familiar in physics, namely a finite non-zero Hausdorff dimension which happens to be equal to the golden mean [1] [15] . Normally the Hausdorff dimension of a deterministically constructed Cantor set is. However uniformly distributed randomness leads to a slightly smaller Hausdorff dimension, namely. This randomness is behind and consequently the theory of probability. On the other hand probability is intrinsic to the quantum world and quantum mechanics and it is also an intrinsic form of measure theory which is the theory according to which our Cantor set was deprived of a length and consequently ordinary existence. Mind you there are fat Cantor sets with a positive measure but we are dealing here for the moment with thin Cantor sets of measure zero. So we see that we will all agree that we cannot define in any normal sense a velocity let alone a constant speed of light. On the other hand we all agree and see that at the end of constructing spacetime from scratch we will be able to define velocity and a speed of light. Superficially it seems that we are contradicting ourselves and that we can have our cake and eat it too. Thus a pragmatic attitude, which will turn out to be logically consistent, is to use the only non-zero quantity in our pre-spacetime model, namely as a speed of light and call it topological for lack of any better word to describe the beginning of a spacetime in which motion and rest are totally indistinguishable as in the famous paradoxes attributed to the Greek philosopher Xenon of antiquity [20] . Another point of vital importance is that for random media the golden mean features as the KAM [1] [17] condition for stability of an orbit in the absence of dissipative frictional damping while for crystalic media the golden mean is basic to its geometric form. In other words we could not start from anything better for modelling nature than the golden mean [1] - [8] .

We are not at the end of our explanation but rather at its very beginning and the complete explanation can be found from the consistency of the entire present paper and previous papers plus the agreement of the so obtained results with painstaking experiments and cosmological measurements [15] . In the present work we have demonstrated how the smallest effects the largest and vice versa and found that the coupling between the pure dark energy of the cosmos and the dark matter energy is due to the overall magnitude of the entire universe degrees of freedom represented by the symmetry group of the holographic boundary [1] [16] dim SL(2, 7) = 336 plus 16 ‘tHooft renormalons ensuring semi continuity and symplecticity of the surface of our spacetime manifold which is contained in the bulk given in this case by the Cantorian-fractal version of E8E8 Lie symmetry group volume [16] - [21] . We have also seen how the five topological dimensionality of Kaluza-Klein spacetime contains Einstein’s four dimensionality which in turn contains ‘tHooft’s dimensionality where k is again ‘tHooft’s renormalon [7] - [12] . On the other hand this cosmic union is contained again in Witten’s dimensional fractal M-theory spacetime where is Hardy’s quantum entanglement [13] . All the three types of fundamental energies, namely the ordinary measurable energy, the pure dark energy and the energy arise from the interaction with the vacuum, ergo the empty set and the pre-ele- mentary particles, ergo the zero set [15] - [21] . The Hausdorff mass charge of ordinary energy was found to be naturally connected to fractal spacetime dimen-

sionality, namely. This then intersects with the vacuum of the empty set and gives. For dark energy the mass

charge is on the other hand equal to the topological K-K dimension, namely 5 which also acts on the vacuum and gives us which is the totality of the dark energy sector. This sector can then be dissected into pure dark energy and pure dark matter energy [4] [21] . The only difficulty in this dissection is that unlike measurable ordinary energy and the total dark energy, the two components are coupled via the totality of the holographic boundary of the universe as discussed earlier on. Our confidence in the final result, namely dark matter energy density and pure dark energy density

where stems from the fact that the quantitative result agrees exactly with that obtained using two radically different methods discussed in the present paper [15] as well as with accurate cosmic measurements and observations, making a mistake in our theoretical model and computation a probability bordering on unlikely, if not impossible.

As a final word or a final question one may be permitted to ask what did we better understand, physically speaking, thanks to the present analysis? The answer is probably that we now know almost for sure that ordinary energy is basically zero measure fractals and by contrast the dark section resembles a five dimensional Kaluza-Klein massive object which clearly could not be observed directly by 3 + 1 dimensional creatures like us. In turn, this five-dimensional object is in reality two parts, coupled together. One part is fractal-like strings which are basically the dark matter part of the cosmos while the rest, i.e. the second part is a ‘tHooft object resembling an almost four dimensional fractal spacetime structure that is slightly smaller than our more familiar Einstein four dimensional spacetime. This is definitely not the last word in understanding but we feel it is a good step forward and the proof for the correctness of this statement is the incredibly simple solution for the problem of dark matter, dark energy and ordinary energy presented in Section 5 of the present paper.

Acknowledgements

I must admit that without Gerard ‘tHooft’s pioneering work and dimensional regularization my present work could not have been possible.

Cite this paper

El Naschie, M.S. (2017) From a Dual Einstein-Kaluza Spacetime to ‘tHooft Renormalon and the Reality of Accelerated Cosmic Expansion. Journal of Modern Physics, 8, 1275-1285. https://doi.org/10.4236/jmp.2017.88085

References