Journal of Modern Physics
Vol.07 No.11(2016), Article ID:69326,3 pages
10.4236/jmp.2016.711124
Absolute Zero Occurs in Black Holes
Sanjay Sastry
Coastal Centers, South Daytona, Florida, USA

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 June 2016; accepted 13 July 2016; published 29 July 2016
ABSTRACT
The black hole is a region in space in which nothing can escape its pull. The two important parts of the anatomy of a stable black hole are the event horizon and gravitational singularity. The main discussion is regarding the temperature of a black hole. Absolute zero is a state which enthalpy and entropy is zero. The temperature of a black hole approaches the gravitational singularity in which space-time possibly ceases and entropy is zero producing absolute zero or possible sub- absolute zero.
Keywords:
Black Hole, Absolute Zero, Event Horizon, Gravitational Singularity

1. Introduction
Absolute zero is the lower limit of the thermodynamic temperature scale, a state of which the enthalpy and entropy of cooled ideal gas reaches minimum value, taken as 0. The theoretical temperature is determined by extrapolating the ideal gas law; by international agreement, absolute zero is taken as −273.15 on the Celsius scale (International system of units) [1] [2] . The corresponding Kelvin temperature scale sets its zero point at absolute zero by definition.
The laws of thermodynamics dictate that absolute zero cannot be reached using any thermodynamic means. As the temperature of the substance being cooled approaches the temperature of the cooling agent, the variable approaches infinity.
Absolute zero and even sub-absolute zero gas occurs in our natural universe. Absolute zero exists in black holes.
A black hole is a region of space in which the gravitational field is so powerful that nothing, including electromagnetic radiation such as visible light, can escape its pull―a kind of bottomless pit in space-time. At its center, there lies an infinitely small, infinitely dense singularity, a place where the normal laws of physics break down [3] . The theory of general relativity predicted that a sufficiently compact mass can deform space-time to form a black hole [4] [5] . The boundary at the region from which no escape is possible is called the event horizon. Although crossing the event horizon has enormous effect on the fate of the object crossing it, it appears to have no locally detectable features. In many ways, a black hole acts like an ideal black body, as it reflects no light [6] [7] . Moreover, quantum field theory in curved space time predicts that event horizons emit Hawking radiation with the same spectrum as a black body of a temperature inversely proportional to its mass.
At the center of a black hole, as described by general relatively, there lies a gravitational singularity. Gravitational singularity is a region where space-time curvature becomes infinite [8] . For a non-rotating black hole, this region takes the shape of a single point and for a rotating black hole, it is a smear that lies in the plane of rotation [9] . In both cases, the singular region has zero volume. It can also be shown that the singular region contains all the mass of the black hole solution [10] . The singular region can thus be thought of having infinite density. The point at which there is gravitational singularity is where entropy ceases.
The discussion is dealing in black holes with stable systems. Stable systems are inherently self-corrections. If something disturbs them from their equilibrium state, they naturally correct themselves and return to the one equilibrium. Unstable black holes are not self-correcting under perturbations. They are the opposite. Once disturbed, their natural dynamics magnifies the disturbances [11] .
A black hole behaves as though its horizon has a temperature and that temperature is inversely proportional to the hole’s mass; T ≈ (6 × 10−8) M.
Thus as the energy (mass) increases, the temperature decreases. Here misexpressed in units of solar masses (2 × 1033 grams). The temperature is in degrees Kelvin, that is, degrees Celsius above absolute zero.
The formula for the temperature of a black hole is:
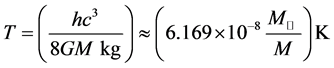
where h is the Dirac constant, c is the speed of light, k8 is the Boltzmann constant, G is the gravitational constant, M is the mass of the black hole and Mʘ is the mass of the sun.
This has important consequences; the bigger the black hole the colder it is, and thus the slower it loses mass.
If this is the case, the temperature approaches absolute zero as a mass from the event horizon gets closer to the gravitational singularity. The possibility of sub-absolute zero occurs inside the black hole at the site of zero entropy, the gravitational singularity.
Ultracold quantum gas made up of potassium atoms recently produced sub-absolute zero. The sub-absolute zero gas mimics “dark energy”; the mysterious force pushes the universe to expand in an ever faster rate against the inward pull of gravity [12] .
Absolute zero occurs past the event horizon and toward the gravitational singularity of the black hole.
There have been multiple theories in relation toward the understanding of temperature and black holes. The only way to satisfy the second law of thermodynamics is to admit that black holes have entropy. Further formulae have been used in the thermodynamic relationship between energy, temperature, and entropy. The Bekenstein-Hawking have attempted to explain such relationship. Further conjuncture using string theory and loop quantum gravity further offer explanations of entropy and proportionality of the area of the horizon.
Just as there are many astrophysicists, theoretical physicists, experimental physicists, etc., there are many explanations about the possibilities of properties of a black hole. Temperature of a black hole is included in one discussion of the properties.
2. Discussion
When discussing about temperature of a black hole, a clarification of the definition of temperature itself is very important.
Temperature is a measurement of the amount of random kinetic energy in a macroscopic system. This definition is generally incorrect. A more acceptable definition is, for two macroscopic systems that can exchange energy, and energy will be transferred from the higher temperature object to the lower temperature object.
In order to determine the temperature of a system, determination which way energy will be transferred to or from another system is required. The two systems will divide up the total energy as to maximize their combined entropy so when the two systems are allowed to exchange energy, there is some transfer of energy that will result in the total entropy being maximized.
Mathematically, the important quantity is the rate of exchange in entropy with respect to energy for both systems. Temperature is the inverse of that quantity.
In solids, liquids, and gases, temperature does provide a measure of the energy in the system. But for a system of magnets in a magnetic field, when energy increases, the temperature increases to infinity and then heads back to zero.
The basis of current thought is black holes have zero entropy. That would oppose the second law of thermodynamics that entropy cannot spontaneously decrease. I believe that any mass inside a black hole, entropy decrease from the event horizon as it approaches the gravitational singularity. That is why radiation may be emitted at or near the event horizon (Hawking radiation) [13] . But when mass enters the gravitational singularity (center of black hole), entropy is zero as space-time is at a standstill in a stable black hole.
Therefore, as entropy is zero, the temperature becomes absolute zero (or possibly sub-absolute zero).
There is a possibility that while matter at the gravitational singularity (center of black hole) emits no radiation, thereby no energy; the singularity produces absolute zero (or possibly sub-absolute zero). Sub-absolute zero gas mimics “dark energy”, the mysterious force that pushes the universe to expand at an every faster rate against the inward pull of gravity. There is a possibility that the dark energy of the universe is nothing but the product of the gravitational singularity producing sub-absolute zero emission of dark energy.
3. Summary
As a matter gets closer to the gravitational singularity, there will be a point in the black hole in which atoms stop moving because of cessation of space-time. The point is absolute or possibly sub-absolute zero. Therefore, absolutely zero (and possibly sub-absolute zero) does occur in nature.
The point at which atoms are not moving near or at the gravitational singularity. This means that at the very least, absolute zero exists in nature.
Cite this paper
Sanjay Sastry, (2016) Absolute Zero Occurs in Black Holes. Journal of Modern Physics,07,1375-1377. doi: 10.4236/jmp.2016.711124
References
- 1. “Unit of Thermodynamic Temperature (Kelvin)”. SI Brochure, 8th Edition, 13 March 2010 , Bureau International des Poids et Mesures, Section 2.1.1.5. Note: The Triple Point of Water Is 0.01°C, Not 0°C; Thus 0 K Is -273.15°C, Not 0273.16°C.
- 2. Arora, C.P. (2001) Thermodynamics. Tata McGraw-Hill, Noida, 43.
- 3. Wald (1984) General Relativity. University of Chicago Press, 200-300.
- 4. Wald, R.M. (1997) Gravitational Collapse and Cosmic Censorship. arXiv:gr-qc/9710068.
- 5. Overbye, D. (2015) Black Hole Hunters. NSAS.
- 6. Schultz, B.F. (2003) Gravity from the Ground up. Cambridge University Press, Cambridge, 110.
http://dx.doi.org/10.1017/CBO9780511807800 - 7. Davies, P.C.W. (1978) Reports on Progress in Physics, 41, 1313-1355.
http://dx.doi.org/10.1088/0034-4885/41/8/004 - 8. Carroll (2004) Spacetime and Black Holes. 205.
- 9. Carroll (2004) Spacetime and Black Holes. 264-265.
- 10. Carroll (2004) Spacetime and Black Holes. 252.
- 11. Braun, S., et al. (2013) Science, 339, 52-55.
http://dx.doi.org/10.1126/science.1227831 - 12. Wald, R.M. (2001) Living Reviews in Relativity, 4, 6. ar-Xiv:gr-qc/9912119.
http://dx.doi.org/10.12942/lrr-2001-6 - 13. Hawking, S.W. (1975) Communications in Mathematical Physics, 43, 199-220.
http://dx.doi.org/10.1007/BF02345020

