Received 30 November 2015; accepted 26 December 2015; published 29 December 2015

ABSTRACT

The spinning period for a free electron and the periods of spin and orbital motion of the electron in an atomic state have been calculated. We have shown that for a free electron the spinning period is: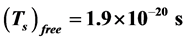. But in the atomic case we show that, both the spin and the orbital periods depend on the quantum numbers n, 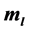, 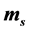and the effective Landé-g factor, 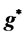which is a function of the quantum number 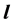of the atomic state 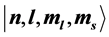given in Dirac notation. We have also calculated these periods for the ground state and some excited states―hydrogen and hydrogen-like atoms. For atomic states the approximate values of spinning period are 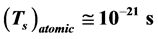and the related orbital periods are: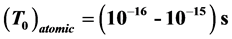. Therefore atto-second processes which are related to the pulse of 10⁻¹⁸ s will filter the orbital motion of the electron but will be long enough to detect the details of the spin motion, such as flip-flops.

Keywords:

Electron Spin, Landé-g Factor, Magnetic Top Model, Spinning Period, Atto-Seconds Processes

1. Introduction

To calculate the periods of spin and orbital motions of an electron in an atomic state 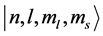in Dirac representation, we consider the total magnetic moment of an electron in the presence of a magnetic field in the z direction. The z-component of the total magnetic moment of electron is given by 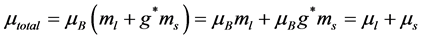[1]

(1)

where 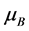is the Bohr magneton, which is given by 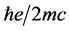and 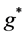is the effective Landé-g factor which takes the values 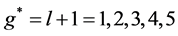depending on the values of the outermost electrons and 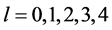(corresponding to the so called states respectively).

To calculate the spin period of an electron, we will use the magnetic top model which was first introduced by Barut et al. [2] . For calculating the period of the orbital motion we will use the current loop model [3] -[7] .

2. Period of the Spinning Motion of Electron

From Equation (1) the z-component of magnetic moment associated with the spinning motion is:

(2)

To proceed further, we calculate the intrinsic magnetic moment of electron with a semiclassical, magnetic top model which was first introduced by Barut et al. [2] .

In the magnetic top model, the spin angular momentum of electron is produced by the spinning of the electronic charge (−e) which is assumed to be uniformly distributed inside a sphere of a radius R. We denote the spin angular frequency of the rotating charged sphere by, then the magnitude of the magnetic moment of this sphere can be calculated(Appendix I) to be

(3)

In the presence of the magnetic field, the z-component of the magnetic moment of the spinning sphere becomes:

(4)

If we compare Equation (2) and Equation (4) we can write:

(5a)

(5b)

where is the spinning period.

Let us consider the equatorial velocity of this spinning sphere,. A simple relativistic argument shows that. Therefore from Equation (5a) we can write:

(6)

Which defines the radius of electron as below:

(7)

For a free electron substituting other related variables in Equation (7) gives us the radius of a free electron,:

(8)

Substitution of Equation (8) in Equation (5b) gives us the spinning period for a free electron:

(9)

which is in good agreement with the semiclassical calculation of Olszewski [8] .

For an electron in an atom, we cannot calculate the radius directly from Equation (7), because we need to know the effective values of. For the same reason we must take the effective values of in Equation (5b) which gives us for the state.

In the following section we find an expression for the period of orbital motion, for the outermost electron in hydrogen and hydrogen-like atoms: which is given by Equation (14):

When we take the ratio of the periods given in Equation (5b) and Equation (14), we find:

(10)

Substituting (from Equation (7)) and with we get:

(11)

It is known that when there is no quantum entanglement, for a free electron, the Landé-g factor is equal to 2. For an electron in an atom the Landé-g factor is given by:

(12)

which varies is in range of. Recently, Saglam et al. [1] showed that because of the quantum entanglements in an atom the Landé-g factor is replaced by the effective g-factor, which takes the values depending on (corresponding to the so called states respectively) values of the outermost electrons together with the unfilled shells respectively. So the maximum values of the effective Landé-g factor, can be as high as 5. Therefore.

If we calculate the effective g-factor, for the ground state hydrogen atom, , we found that. For this value we calculate the period of ground state orbit and find:. Substituting this value and, , , and other related parameters in Equation (11), we find the

spinning period of electron in state,. We give the values of and for the states:, , , and in Table 1.

3. Period of the Orbital Motion of Electron

From Equation (1) the z-component of the total magnetic moment is:

where, , and

Now we find another expression for in the current loop model [2] : we assume that the magnetic moment associated with the orbital motion of electron is produced by the fictitious point charge (−e) rotating in a circular orbit with the angular frequency and the radius in x-y plane. In this model the z-com- ponent of the magnetic moment will be

(13)

If we compare Equation (12) and Equation (13) we write:

(14)

where we replace by; here the subscript (0) stands for orbital motion.

Now we can find the values of for hydrogen and hydrogen-like atoms: especially for states we can put where.

With these replacements Equation (14) becomes:

(15)

We note that the quantum number (l) gets involved through the effective Lande-g factor, which takes the values.

For example, for the ground state of hydrogen atom, substituting and the other related parameter in Equation (15), we find:

(16)

Similarly for the state the corresponding period is:

(17)

where we put:, , and in Equation (15).

Acknowledgments

Authors from Miami University acknowledge financial support from the National Science Foundation (Grant No. NSF-PHY-1309571).

Cite this paper

ZiyaSaglam,MesudeSaglam,S. BurcinBayram,TimHorton, (2015) The Spinning Period of a Free Electron and the Periods of Spin and Orbital Motions of Electron in Atomic States. Journal of Modern Physics,06,2239-2243. doi: 10.4236/jmp.2015.615229

References

Appendix I: Calculation of the Magnetic Moment of a Spinning Charge, Q Distributed Uniformly inside a Sphere of Radius R

Let us denote the uniform charge density by which is related to the total charge Q by:

(A-I)

where is the charge of the spherical shell with the radius r and thickness. First we want to calculate the magnetic moment of this spherical shell with the surface charge density (). Let us assume that the spinning is about z-axis with the angular frequency,. Let us consider the charge element in the area of the band with the radius () and the thickness () in spherical coordinates:

(A-II)

The current element produced by the rotating band charge with the angular frequency, will be:

(A-III)

The magnetic moment element of this band current will be:

(A-IV)

Integrating over the spherical shell gives us the magnetic moment of this shell,:

(A-V)

If we substitude in (A-V) and integrate over the spherical volume, we find the total magnetic moment of the sphere of radius R:

(A-VI)

Substituting (A-I) in (A-VI) we find:

. (A-VII)