Received 19 October 2015; accepted 20 November 2015; published 23 November 2015

ABSTRACT

A model of the Z boson is elaborated from a revised quantum electrodynamic theory (RQED) by the author. The electromagnetic steady field is derived from a separable generating function with a convergent radial part, resulting in a vanishing net electric charge and a nonzero spin and rest mass. From the superposition of the solutions of two Z bosons with antiparallel spin directions, a model is further formed of a composite boson, the computed mass m_C of which becomes connected with the mass of 91 GeV for each Z boson. This results in a composite boson which is likely to become identical with the heavy particle recently detected at CERN. Both these particles are thus lacking of net electric charge, magnetic field and spin, are purely electrostatic and highly unstable, and have masses close to the value of 125 GeV.

Keywords:

Quantum Electrodynamics, Zero Point Energy, Standard Model and Beyond

1. Introduction

The heavy and unstable particle being recently detected experimentally at CERN [1] [2] has no electric charge, no spin, and a rest mass of 125 GeV. Even if the CERN result is generally being considered as a confirmation of the particle earlier proposed by Higgs [3] , the value of its mass cannot be determined by the theory of Higgs. Quigg [4] has further pointed out that such a particle is perhaps not a truly fundamental one, but is built out of as yet unobserved constituents to form a composite particle.

Recently the author has proposed [5] [6] a composite boson to be formed from the superposition of two Z boson solutions with opposite spin directions. The resulting particle then has basic properties in common with the CERN particle, by having a vanishing spin and magnetic field and becoming purely electrostatic and unstable.

As based on a revised quantum electrodynamic theory (RQED) by the author [7] -[9] , a model of the Z boson has further been developed which results in a relation between its mass and characteristic radial dimension. With a mass of 91 GeV, this results in a characteristic radius of about 10⁻¹⁸ m, in agreement with that estimated by Quigg [4] . This model will be used in the present investigation to determine the distribution of electrostatic and magnetostatic energy of the Z boson model. In its turn, this also results in a relation between the mass of the Z boson and that of the composite particle, as demonstrated by the following analysis. Such a mass relation becomes a function of the distribution of energy density within the Z boson. As seen from the analysis, a variation of the included parameters becomes associated with a minimum of the composite particle mass.

2. A Model of the Z Boson

A characteristic feature of RQED theory, not being available from conventional theory on the vacuum state, is the existence of steady electromagnetic states, leading to models for massive particles at rest. The corresponding potentials can then be derived from a generating function [7] . Such a radially convergent function results in particle models having vanishing net electric charge but nonzero local and intrinsic electric charges of both polarities, a nonzero spin, as well as a nonzero rest mass.

2.1. Basic Relations

The present analysis starts from a separable and axisymmetric generating function

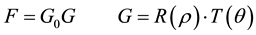(1)

in spherical coordinates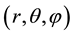. Here G is a dimensionless function, is a characteristic amplitude, and 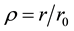a normalized radial coordinate with 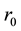standing for a characteristic radial dimension. There is an electrostatic potential 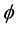and a magnetic vector potential, being sources of the electric and mag- netic field strengths and. The vacuum state [7] - [9] further includes a nonzero electric charge density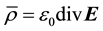, and an electric current density where and c is the velo- city constant of light. The general self-consistent solutions for the electromagnetic components in RQED theory [7] are then obtained from a generating function which takes the form

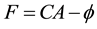(2)

and the electrostatic and magnetostatic potentials are determined by

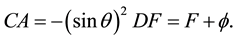(3)

Here the operator 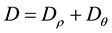has the parts

(4)

and the potentials are given by

(5)

(6)

in terms of the parts R and T of the generating function.

2.2. The Field Strengths

From expressions (3)-(6) the components of the field strengths are now determined by

(7)

(8)

(9)

(10)

With the energy density becomes

(11)

corresponding to a mass density. The total rest mass of the Z boson is then

(12)

2.3. The Energy Distributions

A radially convergent generating function of the form

(13)

is now introduced [7] which includes the two parameters and. The radial part R is finite at, approaches zero at large r, and has its maximum

(14)

at the normalized radius, i.e. at. To obtain a measure of the relative spatial extension of R near the maximum, we define the value of R at the fraction of the radius, i.e.

(15)

The relative extension then becomes

(16)

For a fixed value of the value of then decreases at an increasing, i.e. for an R representing an ever decreasing thickness of a shell localized around the maximum radius.

In its turn the polar part T becomes more concentrated to the equatorial plane at for increasing values of. At large values of both and, the generating function RT thus tends to a spatial distribution being mainly concentrated to a thin ring at the equatorial plane.

With the generating function (13) the normalized field strengths (7)-(10) can be written as

(17)

(18)

(19)

(20)

The mass of Equation (12) is now distributed among the four field components of expressions (7)-(10) and (17)-(20) as given by

(21)

where are the corresponding normalized partial masses.

The distributions of each of these masses can be demonstrated in a two-dimensional space defined by the parameters and, where and represent nested surfaces. The latter surfaces have then different geometries for each partial mass. This also applies to a comparison between the electrostatic mass and the magnetostatic mass.

3. The Composite Boson

3.1. Basic Relations

A superposition is now made of two Z bosons having the same electrostatic potentials given by Equation (5) and opposite cancelling magnetostatic potentials due to Equation (6) with. This results in a purely electro- static composite boson, having an electric field strength of double the value given by Equations (7) and (8), and with no total magnetic field and spin. The resulting particle is expected to become highly unstable, due to its lack of a counter-balancing force due to the magnetic field [7] .

With the definitions (21) the normalized mass of the Z boson becomes. For a doubled electric field strength due to the superposition, the electrostatic mass of the composite particle becomes. Using the experimental value of for the Z boson, the corresponding value of the composite particle becomes

(22)

Here the ratio as well as the mass does not become represented by a system of nested surfaces. Instead the surfaces of constant will at some points intersect in a representation where is plotted as a function of.

3.2. Computed Mass Distributions

The partial masses (21) have been computed from Equations (17)-(21) for various values of and. In most cases and are found to be dominating as compared to and. The electrostatic mass further differs generally from the magnetostatic mass, and there is no equipartition between electrostatic and magnetostatic energy. This affects the computed value of the composite particle mass.

In the experimental investigations on elementary particles of heavy mass, such as those at CERN [1] [2] , an increasing available energy corresponds to a situation in which heavy particle masses are approached from below. Therefore a minimum value of the computed mass will be of main interest. Obtained values of as functions of the radial parameter for a set of values of the polar parameter are demonstrated in Figure 1. Here three domains should be considered [1] :

1) For and the computed values of are higher than the experimentally detected level of 125 GeV at CERN.

2) In the integral of expression (21) the square of the generating function RT of Equation (13) is broadly speaking included. This implies that the domain defined by and will be represented by thin ring-shaped configurations localized close to the equatorial plane. This is confirmed by an example applied to Equation (16) with, resulting in a relative extension of. Such a geometry is far from that of bulky particles and may be put into doubt.

3) Between the two domains 1) and 2) there is a broad window in parameter space given by the range. It represents a high probability of occurrence, also for various forms of geometry as determined by and. This window is in Figure 1 seen to include minimum values of, all being close to the mass of 125 GeV of the particle detected at CERN. The average deviation from this value is only per cent.

The result of Figure 1 can be analyzed as follows. Each curve in the figure represents the values 2 to 6 given to the polar parameter of the part T in relations (13), this as a function of the radial parameter of the part R. The set of curves thus shows that there is generally a minimum of the composite boson mass being close to

the limit 125 GeV for the manifold of particle geometries determined by varying values of and. Further, when performing experiments at increasing available energies, this minimum level will first be approached from below. This implies that a composite boson can and will be created when reaching the same level, before passing to higher levels of available energy.

4. Conclusions

From superposition of the solutions for two Z bosons with antiparallel spin directions, a model of a composite boson has been formed in terms of the present RQED theory. It connects the computed mass of the com- posite boson with the mass of 91 GeV given for the Z boson. Within a large window of the prevailing parameter space, the composite boson mass is found to have a minimum close to the mass of 125 GeV found for the heavy particle detected at CERN.

Due to these results, the composite boson of the present theory is thus likely to become identical with the heavy particle found at CERN. Both particles are namely lacking of net electric charge, magnetic field and spin, are purely electrostatic and highly unstable, and have rest masses close to 125 GeV. The present result has no relation to the theory by Higgs.

Acknowledgements

The author is indebted to MSc Yushan Zhou for a valuable work with the computations of the present analysis.

Cite this paper

BoLehnert, (2015) Minimum Mass of a Composite Boson. Journal of Modern Physics,06,2074-2079. doi: 10.4236/jmp.2015.614214

References