Received 26 September 2015; accepted 27 March 2016; published 31 March 2016

ABSTRACT

In work, dynamics of the spherical loaded clots is studied. For the self-coordinated description of non-stationary processes model representation of potential, obviously time-dependent and allowing construction movement integral is used. Classical and quantum tasks are considered.

Keywords:

Integral of Motion, Poisson’s Equation, Schrödinger’s Equation

1. Introduction

At research of the self-coordinated systems of charged particles in theories of accelerators, in physical electronics, and in physics of plasma movement, integrals in some cases play the defining role theories of bunches. It is possible to specify the theory of electronic rings, the theory of rigidly focusing systems, the kinetic theory of quasistationary conditions of bunches (see [1] - [3] ). The considerable part of the known integrals of the movement which aren’t following from properties of symmetry of system is presented in the work [4] devoted to precisely solved non-stationary potentials in quantum mechanics. Especially fruitful is use of integrals of the movement for the description of systems of the particles interacting with own fields. In the real work, non-sta- tionary ensembles by means of the invariant described in a number of works are studied (see [5] - [7] ). For the description of the self-coordinated systems except this invariant, there is necessary use of the interfaced movement integrals. Possibility of data of the non-stationary quantum system described by the same invariant to system of the ordinary differential equations is shown and private numerical decisions of this system are received.

2. The Classical Self-Coordinated System

We will consider, further, spherically a symmetric task. Hamilton-Jacobi’s equation in this case has an appearance (see [8] ):

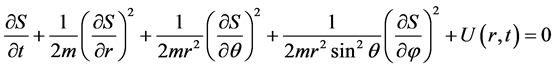(1.1)

Here 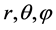-coordinates in spherical system, S-function of Hamilton. We will look for the decision (1.1) in a look:

where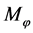―a moment projection to an axis of z,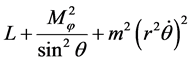―a square of the full moment.

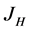―integral interfaced to energy H has an appearance:

.

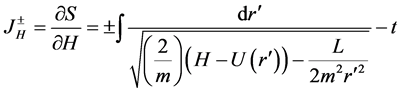Size of 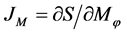and 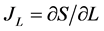also determine by the remaining sizes which aren’t of interest to the task. The Invariant of 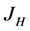can’t be used for the description of non-stationary dynamics of the spherical clot interacting with own field.

We will pass from to the invariant remaining at a certain dependence of potential function from r and t.

We will consider a look Hamiltonian:

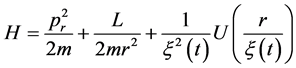(1.2)

Here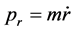. Using expression of a Hamiltonian it is possible to receive expression for an invariant:

(1.3)

where ―a constant. If, further, to enter new variables, that I will assume the air similar to a Hamiltonian. Then similar to integral of can be construct integral, we will consider interfaced to I. Further in this section we will consider that are only particles described by integral (lowering the top index+). In variables the invariant of interfaced to I has an appearance:

(1.4)

Density of particles is expressed by integral in phase space:

(1.5)

We will present an element of phase space in the form:

Averaging on leads to expression:

Thus density of current of has an appearance: can be expressed by dot through I from (1.3):

When using variables: Poisson’s equation assumes an air:

(1.6)

In order that in both members of equation of Poisson there was an identical dependence on multiplier function of distribution has to contain the multiplier which is exponential depending on. We will put:

. We will notice that in variables the invariant of interfaced to I has an appearance (4). If condition is satisfied, that as an independent variable enters Poisson’s equation only. In this case. Thus, we will designate further,

Then follows from Poisson’s equation:

(1.7)

Constant is defined by task parameters, and a charge e: If to use equality of , system (1.7) can be written down in the form of one equation:

(1.8)

Density of particles can be written down in a look:

and density of current:

where

Decisions for the potential of and density of particles of at are given in Figure 1 and Figure 2 at positive and negative values of s. Also To negative values of s corresponds negative value of constant Thus, time of t is limited from below:.

The given expressions for density and current satisfy to the continuity equation:

.

Because density near the beginning of coordinates is equal to zero. In case of positive at any values of coordinate of r size decreases, and density can address in zero, and at negative size grows that can lead to the spasmodic growth of density. The full number of particles grows in the area limited to some value of coordinate beyond all bounds with growth of this value.

Conditions under which there could be states described here demand special research.

3. Quantum Mechanical System

To Hamiltonian (1.2), there corresponds Shrӧdinger’s equation of the following look:

(2.1)

If to enter new variables

That for we will receive the equation:

(2.2)

As well as in the previous section, it is considered that As well as in a classical case, it is

possible to find the private solution of the difficult non-stationary self-coordinated problem on dynamics of the charged quantum ensemble. Thus Schrӧdinger’s equation should be added with Poisson’s equation for the potential of field determined by own charge.

The left member of equation after transition from r to variable will contain multiplier. The same multiplayer also left part, i.e. charge density If in a classical task (in previous section) this circumstance

was carried out at a certain dependence of function of distribution on the interfaced movement integral, in the case described by Schrodinger’s equation, existence of the specified multiplayer can be reached at a certain way of division of variables. We will put in (2.2). It is possible to receive:

(2.3)

(2.4)

(2.5)

These equations have to be added with Poisson’s Equation. Density of a charge has an appearance: to where -the characteristic density of particles. Then with spherical symmetry

(2.6)

We will enter, further, dimensionless sizes: The system of the equations assumes an air:

(2.7)

We will put, further, and we will solve system under entry conditions of where we will put.

Results are represented on Figure 3 and Figure 4.

where -a component of density a stream of probability:

4-D spherical clot

Schrödinger’s equation for a particle in the non-stationary field described by the potential of a look (1.1) has an appearance:

(3.1)

We will consider a 4-dimensional case. We will enter, as well as in the previous sections of variables Equality (3.1) is given to a look:

(3.2)

In (3.2) point means derivative, operator -in variables.

We will put, further,. We will receive the equation for:

(3.3)

This equation differs from the considered equation for a 3-dimensional case first, that the size equivalent to a square of the full moment is considered equal to zero here, and, above all-in the right part don’t have composed,

proportional. The last circumstance allows to divide variables in Schrödinger's equation at any dependence.

The charge density determined by function has an appearance:

,

and the equation for potential:

As in variables the task is stationary, it is possible to put: Here -energy of the connected state. In this case, division of variables doesn’t demand look task.

Thus, we have nonlinear system of the ordinary differential equations of the 4th order:

(3.4)

We will enter dimensionless variables in (3.4): we will designate: where We will receive system:

(3.5)

As it is possible to see in Figure 7, amplitude decreases in the presence of fluctuations from the very beginning monotonously. At the same time the potential (Figure 8) sharply decreases at an initial stage and further changes very slowly.

4. Conclusions

The problems studied above were considered also in works [9] [10] .

Cite this paper

Alexander Chikhachev, (2016) Dynamics of the Spherical Charged Clots. Journal of Modern Physics,07,543-551. doi: 10.4236/jmp.2016.76057

References