Journal of Modern Physics
Vol.06 No.13(2015), Article ID:60681,12 pages
10.4236/jmp.2015.613188
The Relativity of Cosmic Time: The Universe Is a Black Hole
Pascal Churoux
Montgailhard, France
Email: pascal.churoux@free.fr
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 September 2015; accepted 25 October 2015; published 28 October 2015;
ABSTRACT
Up to now, cosmology metrics have been based on Einstein relativity, established in 1905. Hubble has discovered the correlation between redshift and distance. Cosmology interprets the redshift as an expansion effect a(t) through the ΛCDM model. We have proposed a new theory to explain Hubble law. The theory has been validated against observation data. It proposes a new approach of time which introduces the cosmic time tc. Cosmic time is an absolute reference to universe. It is zero at the edge with tc = 0, tc = T at the observer position and tc = s for any source between the edge and the observer, with T > s > 0. This theory acts like the relativity of space-time. The redshift is interpreted as a perspective parameter p(tc) = tc/T. Using gravitation, it is the Einstein effect applied to the universe. This paper comments and interprets further consequences of this new theory. We emphasize the difference between duration (as usually used in classical cosmologic metrics) and the cosmic time tc as a notion of date. It induces two related effects: relativity of speed of light and time stretching. We explain why the cosmological standard model is not well suited to describe the Hubble law, to describe the universe. We also explain why gravitation and temperature increase when going from the center to the edge of the universe, when going from present to birth. The model has no use of black energy. As a consequence, the universe is seen as a black hole created by the cosmic time shock wave when tc = 0.
Keywords:
Hubble Law, Space-Time, Relativity, Light Speed, Universe Expansion, Redshift, Big Bang, Black Hole, Cosmic Time

1. Introduction
Up to now, cosmology metrics have been based on Einstein relativity, established in 1905. Hubble has discovered the correlation between redshift and distance [1] . Cosmology interprets the redshift as an expansion effect a(t) through the ΛCDM model [2] .
In [3] , we have proposed a new theory to explain Hubble law. The theory has been validated against data from [4] . The µ-z diagram is explained without any matter effect and based on the cosmic time parameter. We are suggesting here explanations and interpretations of this theory. All of them are oriented toward a time and space-time interpretation of physics.
Here, we hereby detail the theory from [3] in a different way to emphasize the analogy with the eikonal theory. In Section 2, we develop the main propositions based on the cosmic time and the associated metric. In Section 3, we discuss current metrics. Section 4 deals with gravitation and discuss the edge of the universe. Section 5 gives physical interpretation of the Schwarzschild metric using the generalized refraction index. At the end, in Section 6, we suggest that the relation between cosmic time, gravitation and temperature is connected to the evolution of matter. We conclude in Section 7.
2. The Relativity of Cosmic-Time
We develop the theory of the relativity of cosmic time already proposed in [3] . Here, we present it in a different way (Equation (2B)) to be compatible with a space-time or time stretching interpretation of phenomenon. Cosmic time tc is an absolute date and not a duration as time is commonly used. It is a boundary condition, at the end of the experiment, at the end of the optical path. In classical cosmological science, the cosmic time is already defined as the relative time in the “Big Bang” model integrated over the whole universe.
The observer is measuring waves at cosmic time tc = T. An observed source emits light at cosmic time tc = s. The delay time τ between source and observer is:
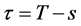 (2A)
(2A)
The relativity of Cosmic Time theory is defined by the factor z, where z is the redshift effect with:
 (2B)
(2B)
c = 299,792,458 m/s (from [5] ) is the speed of light of the observer out of any acceleration field. We introduce the parameter p = s/T as a perspective effect. Interpretations of p and c(s) will be discussed later. By definition, s < T because the source emits light before the observer detects it and so z + 1 > 1.
The distance between the emitting source and the observer is defined by the product of the space-time relation of the observer with the delay τ:
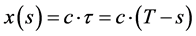 (2C)
(2C)
Let’s note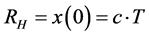 , the universe radius also called the Hubble radius.
, the universe radius also called the Hubble radius.
Figure 1 illustrates the space-time (x/c,tc). It is bounded to the observer. The light cone is defined by Equation (2C). Out of any acceleration field, cosmic time T is orthogonal to the space which is surrounding the observer with αT = 90˚ and βT = 45˚.
For simplicity we deal with one dimensional space phenomena so that space is described with only one dimension. This two dimensional space is defined according time. The fundamental reason is that, from the observer point of view, time is always increasing. He doesn’t move in his own referential, but his proper time is always going on. An observed source can remain static but its own time is generally increasing, out of the edge of black holes.
The observer cosmic time T acts as “a torch lamp” carried by the observer and directed toward the “nadir”. It is lightening non-uniformities of the space path: waves, particles and matter around the observer. When looking out of the “nadir”, he is watching emitting sources (other events).
The observed source is Ms(x/c,s). When a photon is emitted by the source, it vibrates at the cosmic time level s. At this time, the observer is also at the cosmic time s. He cannot see this light. When time increases from s to T, it will be seen by the observer when the emitting source will enter in his field of view, in his light cone.
We see in Figure 1 two interpretations of the same physical phenomenon:
・ The angle βs is no more equal to 45˚. The apparent light cone in the space-time of the source has changed with tg(βs) = p−1. It is a change of space-time effect: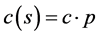 .
.
・ The angle αs is no more equal to 90˚ with sin(αs) = p−1. It is the time stretching effect.
We can illustrate theses two effects as follow:
Figure 1. Illustration of the relativity of cosmic time theory.
・ Example 1: In matter, we use the refractive index n and we assume that the inner speed of light has changed with cn = c/n. Moreover, we define the inner wavelength λn = λ/n and it creates a redshift effect when going out.
・ Example 2: When we look far away, any moving object seems to be moving slower than if it were near us; it is a transverse effect which modifies the speed. Moreover, all dimensions are reduced due to the perspective effect. When the object comes to the observer; that is a radial effect which modifies the apparent size. It is a space stretching effect. This explains why we introduce the time perspective parameter p = s/T.
Effect 1: When dealing with a change of space-time, the local speed of light changes so dimensions are stretched with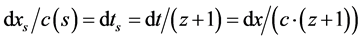 , this is the Tolman Surface Brightness effect.
, this is the Tolman Surface Brightness effect.
Effect 2: The time stretching effect implies a change of frequency of any local temporal phenomenon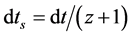 .
.
The way to use these effects in physics depends on the experiment. A static source with dx = 0 is the simpler one. When dealing with a transverse configuration the both effects act. If we come back to example 2, the mobile is both seen moving (its position is changing) and its size is changing to. This explains the difficulty to take the good effect and the mistakes that can easily be done when describing an experiment. This difficulty will be discussed in Sections 3 and 5.
Energy conservation is applied as in the standard model because the proposed model acts in the same way on both a space-time change (Effect 1) and a redshift effect (Effect 2). Staying at a phenomenological level, when changing space (between the source s and the observer T), space and time change, so that any mathematical integration creates a (z + 1)−1 factor: one for each of the three spatial dimensions and one for time.
Application 1: Applied to the photon, energy conservation is a stretching time effect (Effect 2), 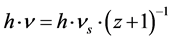 .
.
Application 2: The radiance (in W/m².sr/Hz) measurement is an imaging observation through a spectral filter. It is an application of space-time effect (Effect 1) with two spatial dimensions and one in the time dimension (in a spectral filter) (Effect 2). When changing space-time from the source to the observer the radiance must be divided by the factor (z + 1)3: with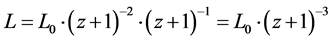 , where L is the measured radiance and L0 is the intrinsic one.
, where L is the measured radiance and L0 is the intrinsic one.
Application 3: The total energy of the black body is the volume integration (three dimensions) of the spectral density energy over all frequencies (one dimension). So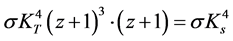 ; where
; where
σ = 5.670373(21) × 10−8 W∙m−2∙K−4 from [5] is the Stephan-Boltzmann constant. We derive: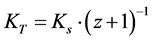 , and:
, and:
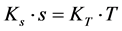 (2D)
(2D)
In cosmology, the configuration of the µ-z diagram (Hubble law) is radial experiment. We have derived (see Equation (A4) in Annex 1) the Hubble law, with:
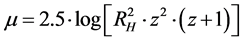 (2E)
(2E)
When z tends to 0, the proposed theory is the same as the current one from the ΛCDM model, with . We have shown the very good agreement between theory and observations from [4] . with RH = 4.2 × 109 pc and T = 13.7 × 109 years. This value is in very good agreement with the current universe age from [6] . Neither critical mass nor black energy is needed to explain observations from Equation (2E). Due to the good agreement between the proposed theory and observations, we may deduce that on average, the universe is flat and cosmic time gives a good description of cosmology science.
. We have shown the very good agreement between theory and observations from [4] . with RH = 4.2 × 109 pc and T = 13.7 × 109 years. This value is in very good agreement with the current universe age from [6] . Neither critical mass nor black energy is needed to explain observations from Equation (2E). Due to the good agreement between the proposed theory and observations, we may deduce that on average, the universe is flat and cosmic time gives a good description of cosmology science.
3. The Space-Time and Associated Metrics
Einstein relativity [7] [8] and derived metrics concern durations only and do not refer to absolute time. Current physics laws are based on differential effects; they are locally valid using the constancy of speed of light.
When the observer is looking at a “moving matter event”, the relative time t is taken into account. For example, the observer considers that the source is moving from Ms1 to Ms2. and ds is the time source increase. The source is not moving in its proper referential and moves from Ms1 to Ms3 in the time-space diagram.
The associated metric is derived from the scalar product. dt is the time distance between events and defined by the Pythagorean theorem in the right triangle (Ms1, Ms2, Ms3) with (see Figure 2):

Equation (3A) considers that the source is close to the observer. It is the time law of the restricted relativity. In Figure 2: the angle αs is no more equal to αT = 90˚: that is the time stretching effect 

Figure 2. The restricted Einstein relativity.
When comparing Figure 1 and Figure 2, we see that αs acts as an “equivalence principle”. Now, the remote event is far enough so that cosmic redshift is no more negligible. We apply Effect 1 to Equation (3A). The cosmic time of the source is s. The local space-time relation is c(s) and assuming that the physical law is locally valid, Equation (3A) becomes

So, using Equation (2B), we write again Equation (3B) such as:

Equation (3C) is the local restricted relativity around the source (tc = s). We can see the analogy between p(tc) = tc/T and the expansion factor a(t)/a0 linked to the FLRW model. When the universe is analyzed with the FLWR model, the p parameter is considered as depending on: mass, energy and space curvature. The use of Equation (3C) suffers two drawbacks to describe the universe: it creates the expansion phenomenon (bounded to the restricted relativity) and it does not take into account the cosmic time stretching effect.
In Equation (3C), indeed dts is a local time and it has to be corrected with the stretching time. We replace dts (the local relative time-Effect 2) by 


As defined in current metrics, ds is kept in the source space-time. Equation (3D) includes both Effect 1 and Effect 2. We recognize a space-time curvature effect, without any expansion. The general space curvature is explained because cosmic time is centered on the observer, it is a radial effect. Equation (3D) shows how a simple metric defined by Equations (2B) and (2C) can be interpreted with a sophisticated tool and lead to wrong interpretations.
4. Effect of an Acceleration Field: Gravitation
We discuss the analogy between Equation (3D) and the Schwarzschild metric. We compare the two different models: Einstein relativity and relativity of cosmic time to explain the Universe.
4.1. Analyze with the Einstein General Relativity
Space-time is no more flat in presence of an acceleration field. When mass distribution is homogeneous and isotropic like a sphere of matter and when dealing with radial effects, a one dimension space description remains suited. The formalism is described by the well known Einstein general relativity. We consider a massive spherical object with a mass M. The associated Schwarzschild metric (from [7] [8] ) is:

where G = 6.67384 × 10−11 m3/kg/s2, from [5] . Redshift from the Einstein effect appears when light is going from a strong gravitational field toward a weaker one.
We consider an emitting source at the distance r = xe from the object center and an observer at the distance r = xT. From [7] , the gravitational redshift z is:

In Equation (4B), xT and xe are distances from the gravity mass center and outside the massive object. The upper term is related to the observer and the lower one is related to the source. For example, if we send a light from the earth surface toward space, the gravitational field will decrease and light will be affected by redshift; xT is higher than xe so z + 1 > 1.
But, when crossing the Schwarzschild singularity (r = Rs = 2GM/c²) of a black hole from the outside to the inside, in Equation (4A) signs of the spatial and temporal terms change. So, time and space are exchanged. That implies that the Einstein effect is inversed and when going from the edge of the black hole to its center light is redshifted. In the universe, objects are quite uniformly distributed around our own position. We are in the center of the universe with a masse Mu. From the “matter” point of view, the cosmic redshift is the gravitational Einstein effect applied to the universe. This explains the high gravitation field at the edge of the universe and why the Big Bang theory proposes a high gravitation field at the origin. φs is the relative (divided by c²) gravitational potential at the cosmic time s. Equation (4B) becomes:

Nota: Black Hole Properties
A black hole of masse M and radius R is defined by the fact that its liberation speed is equal or greater than the speed of light. So that, even light cannot get out from the object. The derived constraint is based on the energy conservation, for example from [7] :

We introduce Equation (4D) in Equation (4B). If xe = R then z tend to infinite. So, at the edge of a black hole, the redshift tend to infinite. Considering that there is reciprocity, an object for which z tends to infinite at the edge is a black hole. Light cannot go out because any wavelength becomes infinite.
Let ρ be the mean universe mass density, so:

From Equation (4D) and using Equation (4E), at the edge of universe xe = RH, if ρ tend to a critical value ρc so z tends to infinite in Equation (4C). We deduce ρc in Equation (4F) hereafter. This parameter is generally presented (from [7] ) as:

where H is the Hubble constant (with H = 1/T), the numerical application gives ρc~10−26 kg/m3. When studying the universe with a mechanical model this critical value defines the limit when the universe will collapse. Hence the scientific community is looking for matter in order to compare the measured density ρ with ρc.
4.2. Analysis through the Relativity of Cosmic Time
Let’s now analyze the situation using the proposed theory. It is an observational fact that z increases when looking far away. This is the Hubble law. The Cosmologic Microwave Background (CMB) has a redshift near 1000 from [9] . The Big Bang theory stipulates that CMB is not the universe origin, redshift is increasing behind the CMB and temperature is increasing as discussed in Section 5. So the universe is characterized by a redshift that tends to infinite when going to the edge.
From Equation (2B) we easily derive that in the proposed model z tends to infinite, when looking far from us, near the universe edge where s = 0. Equation (2B) explains directly observations without any matter condition (such as presented by Equation (4F)). We may hence draw the conclusion that our universe behaves as a black hole and this is well explained by the relativity of cosmic time.
4.3. Relation between Cosmic Time and Gravitation
We perform the analogy between the two theories through Equation (2B) and Equation (4C):

Our local relative gravitation field φT is very weak so φT << 1, we derive:

When s is decreasing, the equivalent gravitational potential φs increases. When redshift is analyzed with Equation (4B), matter and energy are missing to reach the critical value. Matter creates high frequencies non uniformities of space-time. Low frequencies are more difficult to identify. The light cone is the lower frequency of space-time non-uniformities.
5. The Space-Time and Refractive Index
Using Effect 1, we propose that space-time properties (modified by gravitational fields or as proposed by cosmic time) may be explained using local space-time properties through the generalized refractive index parameter. When analyzing light, in Figure 2, we see that, for photons with a speed of light c, 
5.1. Refractive Index and Photons Path
For a punctual mass M, at the distance r we define the parameter ng(r), where Rs = 2GM/c2 is the Schwarzschild radius and r > Rs such as:

When r decreases, ng(r) increases. Light is deviated toward the direction where refractive index increases, following gradient (ng).
Figure 3 illustrates the configuration. O is the mass center. The black curved line is the light path. Light is
Figure 3. Illustration of the relation between the eikonal theory and the Schwarzschild metric.
coming from the left side; it passes through the point M1 and then M2 and after goes to the right side. r is the distance (O, M1), with 



We apply the Pythagorean theorem in the right triangle (M1, M2, M3), at first order:

The local speed of light is c/ng, we can define (Effect 1) the local times ds and dv with


dv is the local time when the light “goes” from M1 to M2. We consider that the observer is in his local space- time c, he is out of the experiment. So, introducing the stretching time effect (Effect 2), he will measure a time

When including Equation (5C) in Equation (5D), we derive:

Experiment 1: Along the path du, an observer (out of any gravitational field) considers that the local speed of light is

Experiment 2: For radial configuration, in Figure 3, dx = 0, M2 = M4 and du = dr. From Equation (5C) and (5D) we derive

5.2. The Schwarzschild Metric
Using Equation (5A), Equation (5E) becomes:

Equation (5F) is identical with Equation (4A). Figure 3 is the graphical illustration of the Schwarzschild metric. It is the link between light properties using the Maxwell equations through the eikonal theory and the light properties using the general relativity. The relative time is the time along the optical path in the observer space.
Experiment 1: For transverse path such as in gravitational lenses (ds ; 0 in Figure 3), we get from Equation (5F)

In this case, space-time acts as a refractive index
Experiment 2: For radial propagation such as in the Einstein effect, dx = 0 in Equation (5F), we get:

That is the time stretching effect and also the cosmological redshift as explained before. In this case ng is used and not 
In this presentation, the Schwarzschild metric describes a transverse configuration when dx ≠ 0. Equation (5B) is symmetric between dr and dx and we can exchange their interpretation. In this case, dx is the radial distance and ds is the local time on the transverse path. This gives the idea that the redshift is created by an expansion speed such as the restricted relativity could explain.
Cosmology with the standard model is a mixture of the general relativity and the restricted relativity. This leads to wrong interpretations with sophisticated space-time properties. It is not well suited to the Hubble law which is simply a radial configuration with static sources, the stretching time effect derived from the relativity of cosmic time theory can simply describe observations. In the same way, the Eikonal theory (geometrical optics) can be an easier way to explain gravitational lenses.
5.3. Relativity of Cosmic Time and Refractive Index
The cosmic time is a radial configuration and it can also be interpreted as a cosmic refractive index. We relate this refractive index to the relativity of cosmic time theory, out of any local matter, with

By definition the stretching effect is


At the position x related to the cosmic time s, the local relation between x and s is:
We derive from Equation (5J):
This is the metric defined by Equation (2C).
The Eikonal theory applied to the cosmic refractive index explains the Tolman effect through a spatial interpretation. When observing universe the configuration is radial. Photons are coming to the observer following a radial path. But, when observing with an imaging system a weak angle exists αs defined by the picture element angular field. This angle will be increased by the diverging effect because the cosmic refractive index decreases from the light source to the observer.
We easily derive, using the Eikonal theory that the observed angle is αT = αs.n(r). When changing space-time, transverse dimensions increases more than the strict geometric perspective effect. Time is also effected by a perspective phenomenon created by the relativity of cosmic time. This is the Tolman Surface Brightness effect. Physically, light path is not spatially curved. Any spatial representation will suffer limitations.
The local speed of light is
6. Discussion
In current physics, when setting the speed of light c as constant in the universe (and not taking into account the relativity of cosmic time), the whole set of surrounding quantities such as: gravitational fields, relative time (delay) and space (distance) are varying. This assumption leads toward a matter-based description of the universe, including gravitation, strength and sophisticated metrics. The Big Bang theory is based on those ideas and creates: expansion, temperature heating and gravitation increase when time turns back. These effects are locally valid using differential present physics laws. When interpreting z as an expansion parameter a(t) introduced in the Einstein general relativity to derive the ΛCDM model, we consider in this paper that the metric is not well applied. We have explained in [3] why we think that the standard model interprets the universe not only expanding but also accelerating.
When we interpret the redshift effect with the perspective parameter p, the universe is seen under the space- time aspect. The model has no use of black energy. Equation (2B) is the first step that proposes that space-time relationship is not spatially constant when the observer is looking at space. Equation (2C) is the associated metric. We think that the proposed cosmic time theory leads to a simpler description of the universe:
Our observable universe is a “cosmic time shock wave” centered on the observer. It is the “Birth of the inner matter. The front wave is the beginning of cosmic time tc = 0. It defines the edge of the observable universe explained as a black hole. The “cosmic time field of view” is defined by the cosmic time limits between 0 and T, from p = 0 to 1, from matter birth to present, from the universe edge to the observer.
When observer cosmic time T increases, RH increases. Keeping the illustration of the “torch lamp”, T acts like an increasing altitude level of the lamp over space. When the altitude of the lamp is increasing, the field of view increases too. From Equation (2C), the universe is seen expanding at the speed of light c. The so-called “expansion” is a consequence of the fact that time is increasing. It is the edge of our field of view which increases. The universe is stable and not expanding; only time is increasing.
When we wonder what will be the future of the universe expansion, we think that a better question is what will be the cosmic time behavior? We have shown that when considering that the universe is flat, the model is well suited to observations. Low frequency distortions may exist but with a weak amplitude. The critical matter density is not a pertinent way to analyze the universe behavior.
In Section 4, we have shown that when the cosmic time decreases gravitation increases. It explains the high gravitation field at the origin of the Big Bang theory. Equation (2D) suggests that the product K.T is constant. Today, based on the cosmic background radiation temperature from [7] with K = 2.725 ˚K and T = 13.7 × 109 years from [5] , we get K.T = 1.18 × 1018 K.s. When cosmic time decreases temperature increases. Gravitation and temperature and pressure effects are the leading parameters of matter evolution as a local effect.
Is there any singularity at the edge? The “edge” notion is derived from our space or time point of view. There is a singularity when p = 0, but there is not when z tends to infinite. This last point of view presents the edge as a horizon. This horizon defines the ground level of cosmic time where tc = 0 or p = 0 or z infinite. What was there before the Big Bang is the same question that what is there outside our black hole universe? The answer, from an observer who separates space and time is that there is another time, another space, another universe.
Are we accreting matter from the outside? Yes, when cosmic time is spreading over space and it is depending on the outside matter. In this case, it is seen as an accretion phenomenon when our universe is observed from the outside. Matter position is fixed except local differential movements. Whatever the age of the outside matter, the shock wave returns it to pure energy with high temperature (Equation (2D)) and high gravitation (Equation (4H)) and high redshift (Equation 2B) at the edge. At the horizon, the accreted matter is not observable. It begins to appear in the Cosmic Microwave Background (CMB) non uniformities.
Cosmological observations are fundamentally radial. They are quite isotropic except local non uniformities. The very light first order dipole temperature non uniformities of the CMB (even if affected by our local velocity) validate this conclusion.
What would happen if the observer were to change his observation position? He will travel with his cosmic time. He is changing space position with his own “torch lamp”, the lamp illuminates the field around the observer whatever be his position. He will not turn back time from his own point of view. At the same cosmic time T, in a flat field he will use the same speed of light. From Equation (2B), space-time and redshift will affect his observations. He will see (or extrapolate a model such as the Big Bang theory) a universe centered on his new position.
7. Conclusions
Our basic contribution is the introduction of the cosmic time tc as a new parameter and to consider that space-time is modified by a relativity effect which may be a leading point of view to describe physics. The cosmic time related to relativity of cosmic time is an absolute reference. The physical gauge of such a theory has been investigated by J. P. Petit in [12] based on the variation of speed of light point of view. We think that cosmology of universe is a space-time effect. It is from our natural experience that we interpret space and time as separated parameters. We may interpret: redshift, universe expansion and acceleration in [3] , Hubble law in [3] , increasing temperature and gravity and naturally decreasing matter age from the center to the universe edge, black holes. In the proposed theory, black energy and critical density are not useful for cosmic universe explanations.
The study of black holes from the outside could be useful to unify big bang and black hole theory. Cosmology and physics could be oriented toward a pure time point of view of phenomena even local ones.
Acknowledgements
A big thank you to my family and friends who have encouraged and helped me. Thanks to Maucherat J. and Mercier C. for the scientific exchanges.
Cite this paper
Ferreira, V.R.F., de Souza, J.A., das Graças Cardoso, M., de Lima Guimarães, L.G., Brandão, R.M., Souza, R.V., Soares, L.I., Nogueira, J.O., Cravo, F.D. and Nelson, D.L. (2016) Evaluation of the Coagulating Potential of the Crude Extract from the Barbatimão Bark for the Treatment of Dairy Effluents. American Journal of Plant Sciences, 7, 1685-1692. http://dx.doi.org/10.4236/ajps.2016.713159
References
- 1. Hubble, E. and Humason, M.L. (1931) The Astrophysical Journal, 74, 43.
http://dx.doi.org/10.1086/143323 - 2. Suzuki, et al. (2011) The Astrophysical Journal, 746, 85.
http://dx.doi.org/10.1088/0004-637X/746/1/85 - 3. Churoux, P. (2015) Journal of Modern Physics, 6, 1227-1232.
http://dx.doi.org/10.4236/jmp.2015.69127 - 4. Marosi, L.A. (2014) Journal of Modern Physics, 5, 29-33.
http://dx.doi.org/10.4236/jmp.2014.51005 - 5. NIST Standard Reference.
http://physics.nist.gov/cuu/Constants/index.html - 6. Wang, X.F., et al. (2006) The Astrophysical Journal, 645, 488, 505.
- 7. Gourgoulhon, E. “Relativité générale”.
http://luth.obspm.fr/”luthier/gourgoulhon/fr/master/relat.html - 8. Hirata, C.M. (2012) Lecture IX.
http://www.tapir.caltech.edu/~chirata/ph236/lec09.pdf - 9. Wright, E. (2001) Cosmic Microwave Background, Encyclopedia of Astronomy & Astrophysics.
http://dx.doi.org/10.1888/0333750888/1634 - 10. Meneghetti, M. “Introduction to Gravitaional lensing”.
http://www.ita.uni heidelberg.de/~massimo/sub/Lectures/gl_all.pdf - 11. Mercier, C. (2011) The Speed of Light May Not Be Constant.
www.pragtec.com/physique
Annex 1: The Hubble Law
Using Equations (2B) and (2C), we derive:

When measuring a radiation, we assume that it follows a law such as:

where L is the measured radiation, x is the distance from object to observer. That is due to the assumption of the energy conservation so the product Fobs∙x2 remains constant. Propagation reduces the flux by a factor (z + 1)3 (see Application 2 in Section 2). So that:

where L0 is the intrinsic radiation. We deduce from Equations (A1), (A2) and (2C):
So,
The magnitude is defined by
So,
where
The distance modulus μ is defined by μ = m ? m0. So:

L. A. Marosi proposes in [4] an empirical law (from 280 measurements), Figure A1 illustrates the good agreement between the two models.
Figure A1. μ-z diagram. Solid line: Relativity of cosmic time theory with RH = 420 × 106 tenth of parsec Equation (A4). Dashed line: the empirical model from Marosi [4] μ = 44.109769 z0.059883.











