Journal of Modern Physics
Vol.06 No.11(2015), Article ID:59749,17 pages
10.4236/jmp.2015.611158
Quantum Entanglement in Coupled Lossy Waveguides Using SU(2) and SU(1, 1) Thermo-Algebras
Naveen Kumar Mogurampally1, K. V. S. Shiv Chaitanya2, Bindu A. Bambah1
1School of Physics, University of Hyderabad, Hyderabad, India
2Department of Physics, BITS-Pilani, Hyderabad Campus, Hyderabad, India
Email: naveenhere928@gmail.com, chaitanya@hyderabad.bits-pilani.ac.in, bbsp@uohyd.ernet.in
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 July 2015; accepted 18 September 2015; published 21 September 2015
ABSTRACT
In this paper, the master equation for the coupled lossy waveguides is solved using the thermofield dynamics (TFD) formalism. This formalism allows the use of the underlying symmetry algebras SU(2) and SU(1, 1), associated with the Hamiltonian of the coupled lossy waveguides, to compute entanglement and decoherence as a function of time for various input states such as NOON states and thermal states.
Keywords:
Coupled Waveguides, Thermofield Dynamics, Master Equation, Lie Algebras, Entanglement, Decoherence

1. Introduction
Recently, there has been a lot of interest in studying entanglement using coupled waveguides [1] [2] . Specially designed photonic waveguides have provided a laboratory tool for analyzing coherent quantum phenomena and have a possible application in quantum computation [3] . The entanglement between waveguide modes is at the heart of many of these experiments and has been widely studied [4] . Using coupled silica waveguides Politi et al. [5] have reported control of multiphoton entanglement directly on-chip and demonstrated integrated quantum metrology opening the way for new quantum technologies. They have been able to generate two and four photon NOON states on the chip and observe quantum interference, which further enhances the capabilities for quantum interference and quantum computing. Among various types of entangled states, NOON states are special with two orthogonal states in maximal super position thus enhancing their use in quantum information processing [6] .
For the efficient use of these waveguides in the field of quantum information, the generated entanglement should not decohere with time [7] . It is well known that the losses have a substantial effect on the wave guides; therefore, the time evolution of the entanglement has to be determined and thus it is of interest in the context of quantum information processing using lossy waveguides. The entanglement between waveguide modes and how loss affects this entanglement has recently been studied by Rai et al. [4] , by using a quantum Liouville equation. In this paper, we approach this problem from the viewpoint of thermofield dynamics [8] . This formalism has the advantage of solving the master equation for both pure and mixed states, converting thermal averages into quantum mechanical expectation values, by doubling the Hilbert space. The formalism thus makes it simpler to calculate the effects of noise and decoherence in the coupled two-mode waveguide system. We look at the effect of different type of input states and show the efficiency of the states for quantum information theory.
Thermofield Dynamics
Thermofield dynamics (TFD) [8] -[12] is a finite temperature field theory. It has been applied to many branches of high energy physics and many-body systems. TFD has been used to solve the master equation, which helps in studying the temporal evolution of entanglement. In particular, it has been used to study entanglement in the presence of a Kerr medium using an SU(1, 1) disentanglement theorem for arbitrary initial conditions by reducing it to a Schrodinger-like equation [13] [14] . Thus, all the techniques available to solve the Schrodinger equation can be used to solve the master equation. We derive the effect of losses giving rise to decoherence by solving the master equation exactly, using TFD, and then compute the decoherence and entanglement properties of some two-mode waveguide systems.
The basic formalism of TFD is as follows: corresponding to the creation and annihilation operators
 and a, which act on the physical space
and a, which act on the physical space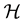 , we introduce “thermal or tildian” operators
, we introduce “thermal or tildian” operators
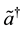 and
and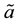 , which act on an augmented (fictitious) space
, which act on an augmented (fictitious) space
 [15] -[17] . The operators a and
[15] -[17] . The operators a and
 commute with
commute with
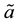 and
and
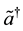 and the sets of basis vectors
and the sets of basis vectors
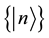 and
and
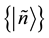 span the Hilbert spaces
span the Hilbert spaces
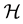 and
and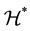 , respectively, and
, respectively, and
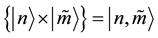 are the basis operators of the doubled Hilbert space, such that the identity operator is
are the basis operators of the doubled Hilbert space, such that the identity operator is . We define a temperature dependent “thermal vacuum state”,
. We define a temperature dependent “thermal vacuum state”,
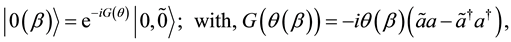 (1)
(1)
where,
 and the corresponding thermal number distribution is
and the corresponding thermal number distribution is






where the state



In TFD, the master equation is

where,



2. Coupled Waveguide System
In optical communications, coupled waveguides are used as transmission medium. The linear coupling between two wave guides is used to transfer the power one wave guide to another. To study the decoherence and entanglement properties of the two coupled waveguides, the model of Rai and Agarwal [4] is used.
The Hamiltonian described by,

where mode a corresponds to first wave guide and mode b corresponds to the second waveguide. The mode a and b obey bosonic commutation relations. The evanescent coupling in terms of distance between the two wave guide is given by J. The density operator has a time evolution given by

In the presence of a damping term (system reservoir interaction), the evolution equations are governed by the Liouville equation

where,

where

In absence of loss, the Heisenberg Equations for the field operators give their time evolution as,
To study the entanglement and decoherence properties as function of time for the coupled wave guide system, we solve the exactly master Equation (7) using TFD. This allows us to study the response to the coupling of different input states such as number, NOON and thermal states, in the coupled waveguide system. In particular, we will show that in the absence of damping, an input vacuum state evolves into a two mode SU(2) coherent state. In the presence of damping, we show that the vacuum state evolves into a two mode squeezed state and a thermal state into a thermal squeezed state.
2.1. Two Coupled Waveguides without Damping (g = 0)
The time evolution of the density operator corresponding to the two coupled waveguides without damping consisting of fields in the modes a and b from Equations (4), (5) is determined by,

Now we apply the TFD-formalism (Equation (3)), by doubling the Hilbert space and get the Schrodinger type wave equation

here, the Hamiltonian


and can be decoupled into non-tildian and tildian parts:

where,


Then the solution of Equation (9) is given by

where,


It is clear from the above that, the two Hamiltonians H and

To calculate the decoherence and entanglement properties of the coupled lossy wave guide as a master Equation (8), (equivalently, the Schrodinger like Equation (9)), the underlying symmetries associated with the Hamiltonians (Equations (11), (12)) are used. To see this symmetries explicitly we define the following operators.

which satisfy the SU(2) algebra,

with number operator,
The Hamiltonian from Equation (11) in terms of the SU(2) generators is,

Hence, the underlying symmetry of the Schrodinger like Equation (9) is



Using the disentanglement formula [18] [19] , and taking the initial state


here,
The density matrix in the number state basis is given by
where,

The entanglement properties are calculated by taking the partial transpose of



The eigenvalues are


Entanglement Properties of the System
For a bipartite system, the entropy is defined as the von-Neumann entropy of the reduced density matrix traced with respect to one of the systems as

such that



We can also quantify the entanglement of the system by studying the time evolution for the logarithmic negativity [21] , which is an easily computable measure of distillable entanglement. For a bipartite system described by the density matrix,


where






Now we consider various cases of optical input states.
Case-1: For two photon system as an input (i.e., N = 2):
The entropy of entanglement of the two photon input state (both



which is shown in dotdashed curve of Figure 1(d). In this case, at time t = 0, we begin with a separable input state and thus the value of Entropy of entanglement (S) is zero. Then the value of “S” increases and attains a maximum value of 1.5 at Jt = 0.785212. Then decreases and eventually becomes equal to zero at Jt = 1.57061. Thus the state becomes disentangled at this point of time. At later times we see a periodic behavior and the system gets entangled and disentangled periodically. We do not see any interference effects.
Now we consider the logarithmic negativity of the various two photon states, as this is different for various two photon states, unlike the entropy.
Case-1 (a). If we take the input state as



which is shown in thick curve of Figure 1(a). At time t = 0, we begin with a separable input state and thus the value of log negativity is zero. EN increases with time and attains a maximum value of 1.32875 for Jt = 0.42879, this is the maximally entangled state. Further, for Jt = 0.785212 we get the dips at EN = 1 (the coincidence rate of the output modes of the beam splitter will drop to zero, when the identical input photons overlap perfectly in time), due to Hong-Ou-Mandel interference [22] and for Jt = 1.57061, EN vanishes. At later times, we see a periodic behavior, attributed to the inter-waveguide coupling (J).
Case-1 (b). Now we take the input state as





which is shown in dotted curve of Figure 1(a). In this case, EN increases and attains a maximum value of 1.32193 at Jt = 0.785212, then decreases and eventually becomes equal to zero at Jt = 1.57061. Thus the state
Figure 1. (a) Shows the time evolution of log negativity for a two photon system: the thick curve shows the result for





becomes disentangled at this point of time. At later times we see a periodic behavior and the system gets entangled and disentangled periodically. Unlike the earlier case for the



Case-1 (c). For two photon input NOON state:



Then the logarithmic negativity of this state is

which is shown in thick curve of Figure 1(c). At time t = 0, we begin with an entangled

Case-2: For four photon system as an input (i.e., N = 4):
The entropy of entanglement for four photon system:

This is shown in dotted curve of Figure 1(d). In this case, at time t = 0, we begin with a separable input state (Entropy of entanglement (S) = 0) after which the value of “S” increases and attains a maximum value of 2.03064 at Jt = 0.785212, it then decreases and eventually becomes equal to zero at Jt = 1.57061. Thus the state becomes disentangled at this point of time. At later times we see a periodic behavior and the system gets entangled and disentangled periodically.
Now we consider the logarithmic negativity for each of the four photon states

Case-2 (a). For the input state as





Then the log negativity entanglement of this system is,

which is shown in thick curve of Figure 1(b). The system starts at t = 0, with a separable input state and log negativity zero, which increases at Jt = 0.200242 to EN = 1.15181 and for Jt = 0.325477 dips at EN = 1 due to Hong-Ou-Mandel interference [22] . The EN increases with time and attains a value of 1.77519 for Jt = 0.601094, this is the maximally entangled state, and for Jt = 0.785212 again we get dips at EN = 1.7277 due to Hong-Ou- Mandel interference. At later times, we see a periodic behaviorr, attributed to the inter-waveguide coupling (J). Because of involvement of four photons, we can see the double the interference effect of the two photon system.
Case-2 (b). For the input state as




The Entanglement for this system is,

which is shown in dotted curve of Figure 1(b).
Case-2 (c). Now we take the input state as


The Entanglement for this system is,

which is shown in thin curve of Figure 1(b).
Case-2 (d). For four photon input NOON state:





The logarithmic negativity for this system is,

which is shown in dotdashed curve of Figure 1(c). In this case, unlike for the two photon NOON state, the entanglement never goes to zero. This means that increasing the number of photons in a NOON state gives a more robust entanglement which is sustained at large times. To show this we calculate the entropy for entanglement and Logarithmic negativity for a 3-photon and a five photon NOON state. The entropy of entanglement for three photon system is shown in thin curve of Figure 1(d). For three photon input NOON state the entanglement is,

where,

curve of Figure 1(c). Similarly for a five photon system as an input (i.e., N = 5): he entropy of entanglement for five photon system is, shown in thick curve of Figure 1(d).
For five photon input NOON state, the entanglement for this system is,

and
The Logarithmic entropy is shown in thin curve of Figure 1(c). We see that as the photon number increases the NOON state gets more and more robust and shows that “high-noon” states can be used for more precision measurements. These results are relevant in light of the recent experimental detection of entangled 5-photon “NOON” states [23] .
2.2. Entanglement Properties for Input Thermal States
Now we consider the initial state




where,




The entanglement properties are calculated by taking the partial transpose of



The von-Neumann entropy of the reduced density matrix in terms of


Case-3 (a). For two photon system as an input (i.e., N = 2):
The entropy of entanglement for two photon is

which is shown in Figures 2(a)-(c).
Case-3 (b). For four photon system as an input (i.e., N = 4):
Then the entropy of entanglement for four photon system is

which is shown in Figures 2(d)-(f).
These figures show that for low values of



Figure 2. For input two photon system: (a) Shows the time evolution of entropy of entanglement (S) for different values of





2.3. Two Coupled Waveguides with Damping (g ¹ 0)
We consider now, losses in the coupled waveguides due to system-reservoir interaction with “g” as the rate of loss due to the material of the waveguide. The time evolution of the density operator equation is

with,

the following transformations,


gives

We diagonalise this Hamiltonian by applying a squeezing (Bogolubov) transformation mixing the real and tilde fields.


where,


and





where,


and





and satisfy the commutation relations

The Casimir operators are

Then the solution of Equation (45) becomes

where,

By using the SU(1, 1) disentanglement formula [18] , one can write Equation (61) as,

here,

with

subscript i labels A, B.
We consider an initial state

where

2.3.1. Calculation of Entanglement of the System for g ¹ 0
The entanglement properties are calculated by first taking trace of




The entropy of entanglement of the the system is

Thus, for two photon state as an input state, the entropy of entanglement of the system is

which is shown in thin curves of Figures 3(a)-(d).
For four photon state as an input state, the entropy of entanglement of the system,
Figure 3. The time evolution of entropy (S) for two photons (shown in thick curve) and four photons (shown in thin curve): (a) For γ = 0 (without damping); (b) For γ = 0.01; (c) For γ = 0.03; (d) For γ = 0.05, with J = 0.5.

which is shown in thick curves of Figures 3(a)-(d). When


Since the state is Gaussian, we can use the covariance matrix method to calculate the entanglement of the sys- tem by using Simon’s criterion [24] . The density matrix can be written as







Then, the covariance matrix is:

where,



Since the tildian fields are fictitious, we trace over them to get the covariance matrix for the physical modes,

The canonical form of covariance matrix is given by,

where,

Then the separablility condition [24] for any two mode state is

The symplectic eigenvalues are defined as,

where,
and
The entanglement of the system is

For


In order to quantify the decoherence effects, we compute


The behaviour of decoherence is plotted Figure 5. We have considered two cases Figure 5(a), shows the variation of decoherence with time for strong coupling for various values of

2.3.2. Entanglement for Two Mode Thermal State with Damping g ¹ 0
Taking the initial state

Figure 4. (a) Shows the time evolution of entanglement (EN) without damping (γ = 0); (b) Shows the time evolution of entanglement with damping (for different values of γ) with r = 0.25, J = 0.5.

where,




Applying Simon’s criterion Equation (77) we see that the system is entangled iff

For


3. Conclusion
In this paper, we have shown that the formalism of thermofield dynamics is a powerful tool for exact studies of coupled waveguide systems. Indeed, we have exactly solved the master equation associated with SU(2) and
Figure 5. (a) Shows the time evolution of Decoherence for different values of γ with J = 3 and (b) for J = 0.25.
Figure 6. Shows entanglement (EN) vs. thermal distribution function (
SU(1, 1) symmetries for coupled lossy waveguides with and without damping. For coupled waveguides without damping, special attention has been given to the time evolution of the NOON states as inputs and we have shown that as we increase the photon number, the entanglement of the NOON states survives with time, thus making them extremely suitable for quantum information. The solution for damped systems was obtained by transforming the master equation to a Schrodinger type equation and applying the disentanglement formulae for SU(2) and SU(1, 1). Our work extends that of Rai et al. [4] , as it gives the exact solution for the master equation, and, in addition shows how the entanglement behaves for input thermal states. Our results have also shown that the entanglement of the system can withstand a certain amount of damping, suggesting that it can be used for applications such as quantum computation, even if the waveguides are lossy. Furthermore, we have shown the effect of an external heat bath on the system, by applying our methods to thermal input states. Our method shows the usefulness of thermofield dynamics in quantum entanglement problems, quite orthogonal to the approach given in Ref. [25] , and allows us to handle damping in entanglement generation properties. We propose to apply this formalism to coupled light-atom systems, to shed further light on the effect of damping on the generation of entanglement.
Acknowledgements
M.N.K. wishes to acknowledge CSIR-UGC for a JRF fellowship. KVSSC acknowledges the Department of Science and technology, Govt of India, (fast track scheme (D. O. No: SR/FTP/PS-139/2012)) for financial support. We wish to thank Prof. C. Mukku and Prof. S. Chaturvedi for insightful comments. We also wish to thank V. Srinivasan for introducing us to the details of thermofield dynamics.
Cite this paper
Naveen KumarMogurampally,K. V. S. ShivChaitanya,Bindu A.Bambah, (2015) Quantum Entanglement in Coupled Lossy Waveguides Using SU(2) and SU(1, 1) Thermo-Algebras. Journal of Modern Physics,06,1554-1571. doi: 10.4236/jmp.2015.611158
References
- 1. Christodoulides, D.N., Lederer, F. and Silberberg, Y. (2003) Nature (London), 424, 817-823.
http://dx.doi.org/10.1038/nature01936 - 2. Longhi, S. (2009) Physical Review A, 79, Article ID: 023811.
- 3. Longhi, S. (2009) Laser and Photonic Review, 3, 243-261.
http://dx.doi.org/10.1002/lpor.200810055 - 4. Rai, A., Das, S. and Agarwal, G.S. (2010) Optics Express, 18, 6241-6254.
http://dx.doi.org/10.1364/OE.18.006241 - 5. Politi, A., Cryan, M.J., Rarity, J.G., Yu, S. and O’Brien, J.L. (2008) Science, 320, 646-649.
http://dx.doi.org/10.1126/science.1155441 - 6. Rozema, L.A., Bateman, J.D., Mahler, D.H., et al. (2014) Physical Review Letters, 112, Article ID: 223602(5).
- 7. Zurek, W.H. (2003) Reviews of Modern Physics, 75, 715-775.
http://dx.doi.org/10.1103/RevModPhys.75.715 - 8. Umezawa, H., Matsumoto, H. and Tachiki, M. (1982) Thermofield Dynamics and Condenced States. North-Holland Publishing Company, Amsterdam.
- 9. Laplae, L., Mancini, F. and Umezawa, H. (1974) Physical Review C, 10, 151.
- 10. Takahashi, Y. and Umezawa, H. (1975) Collective Phenomenon, 2, 55-80.
- 11. Ojima, I. (1981) Annals of Physics, 137, 1-32.
http://dx.doi.org/10.1016/0003-4916(81)90058-0 - 12. Umezawa, H. (1993) Equilibrium and Non-Equilibrium Thermal Physics. Proceedings of the 3rd Workshop on Thermofield Theories and Their Applications, Banff, World Scientific, Singapore.
- 13. Chaturvedi, S. and Srinivasan, V. (1991) Journal of Modern Optics, 38, 777-783.
http://dx.doi.org/10.1080/09500349114550761 - 14. Chaturvedi, S. and Srinivasan, V. (1991) Physical Review A, 43, 4054-4057.
http://dx.doi.org/10.1103/PhysRevA.43.4054 - 15. Shanta, P., Chaturvedi, S., Srinivasan, V. and Kapoor, A.K. (1996) International Journal of Modern Physics B, 10, 1573-1584.
http://dx.doi.org/10.1142/S0217979296000672 - 16. Shanta, P., Chaturvedi, S. and Srinivasan, V. (1986) Modern Physics Letters A, 11, 2381-2396.
- 17. Chaturvedi, S., Srinivasan, V. and Agarwal, G.S. (1999) Journal of Physics A: Mathematical and General, 32, 1909-1926.
http://dx.doi.org/10.1088/0305-4470/32/10/009 - 18. Perelomov, A. (1986) Generalized Coherent States and Their Applications. Springer-Verlag, Berlin.
http://dx.doi.org/10.1007/978-3-642-61629-7 - 19. Fujii, K. (2002) Introduction to Coherent States and Quantum Information Theory.
http://arxiv.org/abs/quant-ph/0112090 - 20. Agarwal, G.S. and Biswas, A. (2005) Journal of Optics B: Quantum Semiclassical Optics, 7, 350-354.
http://dx.doi.org/10.1088/1464-4266/7/11/006 - 21. Vidal, G. and Werner, R.F. (2002) Physical Review A, 65, Article ID: 032314.
http://arxiv.org/abs/quant-ph/0102117 - 22. Hong, C.K., Ou, Z.Y. and Mandel, L. (1987) Physical Review Letters, 59, 2044-2046.
http://dx.doi.org/10.1103/PhysRevLett.59.2044 - 23. Afek, I., Ambar, O. and Silberberg, Y. (2010) Science, 328, 879-881.
http://dx.doi.org/10.1126/science.1188172 - 24. Simon, R. (2000) Physical Review Letters, 84, 2726-2729.
http://dx.doi.org/10.1103/PhysRevLett.84.2726 - 25. Hashizume, Y. and Suzuki, M. (2013) Physica A: Statistical Mechanics and Its Applications, 392, 3518-3530.




































