Journal of Modern Physics
Vol.06 No.09(2015), Article ID:58779,6 pages
10.4236/jmp.2015.69132
Clusters of Radiation Defects in Silicon Crystals
Hrant N. Yeritsyan1*, Aram A. Sahakyan1, Norair E. Grigoryan1, Vachagan V. Harutunyan1, Vahan A. Sahakyan2, Armenuhi A. Khachatryan2
1A.I. Alikhanyan National Science Laboratory (Yerevan Physics Institute), Yerevan, Armenia
2National Institute of Metrology, Yerevan, Armenia
Email: *grant@yerphi.am
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 July 2015; accepted 10 August 2015; published 13 August 2015
ABSTRACT
While considerable progress has been achieved in radiation influence on the solid states, the quantitative assessment of defect production is very scarce. In this paper radiation defects studies in silicon crystals are briefly reviewed and comprehensively analyzed depending on irradiation energy and dose, paying special attention to electron irradiation in wide energy spectrum when crystal lattice disordered regions (clusters) occur. Electron irradiation, which is a simple way to introduce intrinsic defects, was used as one of the most powerful techniques to study point and cluster defects which affect properties of semiconductors depending on irradiation energy. Fundamental aspects of radiation induced defects are discussed and it is shown that they bring information on the threshold energy for atomic displacement, on the recombination of vacancy―interstitial pair and mainly, on radiation defects cluster formation which essentially influences on the irradiating material properties. The determination of the irradiation critical dose and energy for the formation of homogeneous disordered regions (clusters) are detailed.
Keywords:
Clusters of Radiation Defects, Point Radiation Defects, Irradiation Dose, Irradiation Energy, Semiconductors, Silicon

1. Introduction
It is known that electron industry is mainly based on the application of physical processes, obtained in solid state materials with implementation of external influences, for example, high energy particle irradiations. The nature of these physical phenomena strongly depends on structural defects in there (shifted atoms in crystal lattice, impurity centers etc.) [1] -[5] , which is different depending on irradiation type, energy, intensity and dose.
Starting from 50-s of 20-th century it became possible to control the concentration of defects in solid state material by irradiation of material with high-energy particles (ions, protons, neutrons, electrons and g-quanta) [6] . Besides the concentration of defects, created in material under influence of certain particle beam, depends on beam parameters (energy, dose, intensity) as well as sample temperature and its impurity content [7] -[10] . All these investigations at last established a new radiation implantation “more pure” (avoiding inclusion of foreign mixtures) technology, which allows by irradiation to obtain materials with previously planned physical properties and [6] .
From solid state materials nowadays quantity-produced electron industry (including nano-materials) is based on semiconductors, often silicon (Si) and devices built on it. These materials and devices are using at irradiation environments (particle accelerators, nuclear power stations, cosmic space) and it is important to define their behavior and application limit in these extreme physical conditions depending on irradiation energy and dose. In this respect it is important to separate point (low energy, near threshold) and cluster (extended defects or disordered regions) radiation defect formations because they influence the semiconductors properties differently. The present paper is devoted to discussing and analyzing these problems.
2. Basic Energetic Conditions for Cluster Radiation Defects Formation
The clusters of radiation defects in crystal lattice are forming at irradiation by high energy particles or quanta (incident particles) when their energy is sufficiently high for displacement of lattice atoms from the sites which in his turn are able to displace other atoms developing further collisions and generate of high concentration primary simple defect pairs (Frenkel pairs―Fp): vacancies (V) and interstitial atoms (I). Meantime, an energy threshold Ecl is implemented to characterize the cluster forming condition:
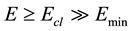 ; (1)
; (1)
where E is energy of incidence particle, Emin is its minimal energy sufficient for displacement of lattice atom from the site to lattice interstitial position. It is obvious from (1) that the Ecl cannot be expressed sharply. Indeed, the term of “threshold energy” for clusters has a defined meaning if taking into account the diffusion of primary simple radiation defects in the crystal and formation of stabile clusters via unstable once, at the same time the energy of incident particles varies smoothly.
In common cases of radiation defect production Emin is defined from the expression
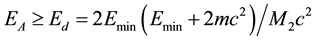 (2)
(2)
at particle relativistic energies, and
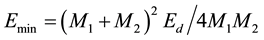 , (3)
, (3)
at solid sphere collisions classic law.
Where Ed is the simple defect pairs (Fp) creation energy, m―electron mass, c―light velocity, M1, M2―are masses of incident particles, and irradiated sample atoms, respectively. The formula (2) may be used in cases of gamma-irradiations too because they cannot cause Fp defects directly, but only via electron-positron pair production, Kompton- or photo-effects. Formula (3) is applied at neutron, proton or ion irradiations.
Note, that the application of thermodynamic approach of adiabatic transition of bonded atom from its main site to interstitial and fix there at given temperature for determination of Ed, allows to obtain reasonable value. In this case the theoretical [11] assumption gives 2 - 3 times higher value for crystals with bonding energy of 10 eV, which is close to experimental data carried out by radiation physics methods. For example, in electron irradiated Si crystals Ed is near 25 eV, Emin = 145 keV, and Ecl is estimated 9 - 10 MeV. In mixed semiconductors the value Ed has complicated character and is high, connected with atom displacement to the different sub-lattices. Here is not taken into account the energy transfer dependence from particle incidence angle which may cause some decrease of calculations results but not influence on the residual once, only maximum energy transfer at small angles may present practical interest [12] .
An important parameter in high energy particle interaction with material atom is cross-section of the process σd, i.e., the probability of Fp production when EA ≥ Ed, and σ(cl) for formation of clusters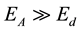 , then the general expression of cross-section can be written:
, then the general expression of cross-section can be written:
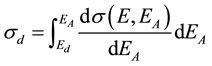 ; (4)
; (4)
At the given cases formula (4) becomes more definite depending on peculiariaties of interaction and type of irradiation, on bonding atoms in irradiated material. Because of the dependences of differencial cross-section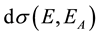 , and hence, the probabilities of energy transfer EA to the medium atoms are different for neutrons and charged particles, then the result of EA distribution is different too. This statement is important because the maximum energy transfer EAmax can be high but the average energy of perviously displaced atoms may be low [13] , which is seen from simplificated expression:
, and hence, the probabilities of energy transfer EA to the medium atoms are different for neutrons and charged particles, then the result of EA distribution is different too. This statement is important because the maximum energy transfer EAmax can be high but the average energy of perviously displaced atoms may be low [13] , which is seen from simplificated expression:
 (5)
(5)
The energy distribution of perviously displaced atoms plays significant role on experimental point of view in investigations of radiation defects production rate, in particular, clusters formation, because of the average distance between elastic collisions of irradiated material atoms depends on their energy, and hence, irradiating particle path. It means that the sample tickness in all cases must be lower with respect to this penetration path. For the cluster formation cross-section it is necessary to apply (4) and empiric data: ;
;
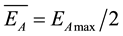 (at neutron irradiation) and
(at neutron irradiation) and 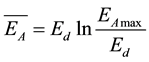 (including irradiation by hard charged particles
(including irradiation by hard charged particles
and protons). At irradiations by charged particles and protons with non-relativistic energies the (4) can be simplificated to:
 ; (6)
; (6)
here b―is the “atomic radius” which defines an acting area of displaced atom.
At electron irradiations for clusters description it is useful only expressions for relativistic energies; corresponding dependencies of 50 MeV irradiations are presented in Figures 1-4.
Figure 1. Energetic dependence of number of primary displaced atoms of Si on the unit path at energy region of 0.1 MeV in Silicon (Si) samples irradiated by electrons with energy 50 MeV.
Figure 2. Energetic losses of 50 MeV electrons in Si on the unit path at energy region of 0.1 MeV.
Figure 3. Dose dependence of di-vacancy absorption band of 960 cm−1 in Si crystal irradiated by electrons with energy 50 MeV: 1―n-Si, specific resistance 100 Ohm∙cm, 2―n-Si, specific resistance 450 Ohm∙cm.
Figure 4. Introduction rate of primary di-vacancies in clusters in silicon crystals depending on irradiation by electrons with energy 50 MeV at different suggesting thresholds Ed.
It can be seen from Figure 1 that primary displaced atoms have much more energy at the energy region near 102 eV and their energy strives to Ed having capability to form further displacement then to rest until capture by impurity or other trapping centers.
3. Primary Displaced Atoms, Their Cascades and Formation of Clusters
No into details of ionization and other energy losses processes, note that for cluster creation it is necessary to develop a cascade of atomic collisions initiated by irradiation and it takes place until the energy exchange between atoms, including previously displaced atom, will decreased in respect to Ed. This process may be considered as inner irradiation of material by intrinsic atoms. The aim of cascade consideration is, first of all, to ascertainment space distribution of V and I in the clusters of primary radiation defects taking into account information on their localization in the other places of crystal and mobility of these point defects. The existence of microscopic areas of high concentration primary defects influences on the number and distribution of defects in the stable cluster consisting of immovable V, I which define the main properties of irradiated semiconductors [14] . The process of stable cluster formation of radiation defects in result of cascade evolution is considered to be consisting of three stages: first―“fastest”, energy transfer from incident particles to the material atom with duration about 10−19 - 10−20 sec; secondary―“fast”, formation of primary simple defects V and I, with duration of 10−13 - 10−14 sec; and third―temperature diffusion of V, I to different impurities, imperfections and creation of stable at given temperature (mostly at room temperatures) clusters of secondary defects with duration about 10−6 - 10−7 sec, the distribution of which may differ from those in primary cluster.
Figure 2 shows the loss of energy from electrons with energy 50 MeV in Si crystal when clusters are formed. In fact these data are in accordance to the Figure 1 which means that more defects are created at the initial stage of electron incidence with high energetic region.
For analytical calculation of atomic collisions in formation of equilibrium cluster condition it is suggested: all collisions are binary which means that the radius of forces is lower than inter-atomic distance in crystal; atoms in crystal lattice are at a rest in beginning state. This static model is reasonable because, for instance, if the Si atom receives Ed, and “fastest” stage is over, the crystal lattice begins relax to near new configuration of radiation defects and after that lattice emits thermal oscillation because this thermal process is much duration. Meantime the main part of Ed was spent as a thermal energy, and potential energy of stabile defects or clusters remained very low from Ed (in the case of Si it is about 5 eV) which may be annealed at high temperatures. Even if the lattice temperature is low for defect diffusion, the field of inner tensions of created Fp-defects can do attractive annihilation between V and I, and no displacement remained in result.
Given situation shows, in one hand, the difficulty of Ed determination as a minimum energy allowing an atom to leave its neighboring atoms and take part in further cascade process. On the other hand, it is important precise Ed determination as a minimum energy which is necessary for non-returnable atomic displacements, i.e. taking into account the lattice response because of this value is measuring in experiment. Besides, if imagine around of interstitial atom all possible vacancy positions for which the instantaneous created Fp defect is non-stable, then a volume of non-stability (or recombination volume) may occur for Fp including about 100 lattice sites. This may lead to self-annihilation of the cluster. Hence, one can observe a high radiation stability of material in case of neutron irradiation rather than gamma or X-ray irradiations which create much lower concentration of Fp but significantly space separated, i.e. stable [15] . That is why when considering primary clusters it is necessary to take into account intrinsic competition between movable V, I, and fixed di-vacancies created in result of captured two vacancies which stimulate forming of stable “frozen” clusters.
4. Number of Displaced Atoms and Radiation Defects in Clusters
In order to estimate the whole number of all displaced atoms it is necessary to assume a cascade function and probability character of energy transfer from initially displaced atom to other atoms of irradiated material. First of all the number of initially displaced atoms in 1 cm3 is expressed by:
 (7)
(7)
where D―is intensity of irradiation dose, t―irradiation time, No―number of atoms in 1 cm3 (for Si No = 5 ´ 1022), σd―cross-section of collisions defining of primary knock-on atoms. Hence, the all displaced in 1 cm3 atoms may be written:

where ύ is the number of averaged on energy atoms knocked-on by primary atom including itself. The dependence of ύ(EA) is calculated consecutively [2] : at elastic collisions the first atom with energy E1 transfers his part to second one





taking into account probability character of radiation defect production, can be estimated:


where Mn, MA are the masses of neutron and irradiated material atom, respectively, f―is a factor of anisotropy, which is not taken into account in this case, in particular, if irradiation by neutrons of materials with atoms of medium atomic weight occur. In case of irradiation by charged particles of materials with light atoms:

The compare of (9) and (10) shows that irradiation by charged particles leads to formation of lower group of defects in respect to neutrons which is due to different scattering in Coulomb field and scattering of neutrons by nuclei.
Considerable role in cluster creation plays di-vacancy which is bonded of two leaved by atoms free sites and has tendency to increase his concentration during irradiation (Figure 3). The rate of their introduction may be estimated by following considerations. Due to high mobility of I in respect to V, an intensive diffusion of I takes place from primary (non-stable) cluster region to the volume of sample and formation V + V = V2, i.e. secondary di-vacancy in the area of creation of clusters of primary defects (Figure 4).
Competing process of running off single V from primary cluster to the volume of sample dominate at low energy of primary displaced atoms, i.e. at relatively low energy of incidence particle. Thus it can be confirmed that the concentration of di-vacancies in cluster equals to the half of vacancies concentration, created in cascade of elastic collisions of primary atoms displacements at energy defined by (5), and number defined by (9) or (10) depending on incidence particle type.
It is important to assume a number of radiation defects on the unit of path (along incident particle), in other words, introduction rate of defects dN/dx both for Fp and clusters which is presented by integrals over Ed to EFp and EFp to Ecl, including corresponding cross-sections. The application of above mentioned statements and (10) allowed to find following results in Si crystals irradiated by 50 MeV electrons: for Fp introduction rate from 1.8 to 2.9 cm−1 and for clusters introduction rate from 0.63 to 0.95 cm−1; number of di-vacancies in cluster―0.332 cm−1, whole number of di-vacancies―0.772 cm−1.
5. Conclusions
From the results of this study one can conclude:
1) Energetic circumstances were analyzed in silicon irradiated by electrons with energy 50 MeV for point and cluster radiation defects creation and energy thresholds were determined about 145 keV and 9 - 10 MeV, accordingly, while Ed for Fp and cluster formations were estimated: 25 eV and 7 keV, accordingly.
2) An important parameter in high energy particle interaction with material atom, the cross-sections of the processes (σd) i.e., the probability of production when

3) The role of di-vacancies in cluster formation was emphasized; their quantitative presence in the disordered region and in the other non-disordered part of the sample was defined which is important for irradiated material characterization.
4) Energetic losses per one 1 cm of the incidence particle penetration were determined in silicon irradiated by electrons with energy 50 MeV.
Contribution of Authors
HY and VS supervised all works and did theoretical calculations, AS and AKH carried out experimental measurements of silicon electro-physical properties, NG and VH carried out optical measurements. All authors took part in active discussion of data and interpretation of results.
Cite this paper
Hrant N.Yeritsyan,Aram A.Sahakyan,Norair E.Grigoryan,Vachagan V.Harutunyan,Vahan A.Sahakyan,Armenuhi A.Khachatryan, (2015) Clusters of Radiation Defects in Silicon Crystals. Journal of Modern Physics,06,1270-1276. doi: 10.4236/jmp.2015.69132
References
- 1. Smirnov, L.S., Ed. (1977) Physical Processes in Irradiated Semiconductors. “Nauka”, Siberian Branch of Academy of Sciences of Soviet Union, Novosibirsk, 256 p.
- 2. Leroy, C. and Rancoita, P.-G. (2007) Reports on Progress in Physics, 70, 493-625.
http://dx.doi.org/10.1088/0034-4885/70/4/R01 - 3. Akishin, A.I. (2007) Kosmicheskoe Materialovedenie. Edition of MGU im. Lomonosova, Moscow, 234 p. (In Russian)
- 4. Makhkamov, Sh., Tursunov, N.A., Ashurov, M., Saidov, R.P. and Khakimov, Z.M. (2001) Semiconductor Science and Technology, 16, 543-547.
http://dx.doi.org/10.1088/0268-1242/16/7/303 - 5. Pagava, T.A. (2004) Fizika i Tekhnika Poluprovodnikov, 38, 665-669.
- 6. Gurovich, B.A., Dolgij, D.I., et al. (2001) Uspekhi Fizicheskikh Nauk, 171, 105-117.
http://dx.doi.org/10.3367/UFNr.0171.200101d.0105 - 7. Barabanenkov, M.Yu., Leonov, A.V., Mordkovich, V.N. and Omel’yanovskaya, N.M. (1999) Fizika i Tekhnika Poluprovodnikov, 33, 537-541.
- 8. Barabanenkov, M.Yu., Leonov, A.V., Mordkovich, V.N. and Omel’yanovskaya, N.M. (1999) Fizika i Tekhnika Poluprovodnikov, 33, 897-899.
- 9. Pagava, T. and Basheleishvili, Z. (2002) Fizika i Tekhnika Poluprovodnikov, 36, 1157. (In Russian)
- 10. Emtsev, V.V., Ehrhart, P., Poloskin, D.S. and Emtsev, K.V. (2007) Journal of Material Science: Materials in Electronics, 18, 711-714.
http://dx.doi.org/10.1007/s10854-006-9103-6 - 11. Seitz, F. and Koehler, J. (1956) Solid State Physics, 2, 307-442.
- 12. Vavilov, V.S. (1963) Interaction of Radiation with Semiconductors. Physical-Mathematics Literature, Moscow, 264 p. (In Russian)
- 13. Emtsev, V.V., Ivanov, A.M., Kozlovski, V.V., Lebedev, A.A., Oganesyan, G.A., Strokan, N.B. and Wagner, G. (2012) FTP, 46, 473-481.
- 14. Watkins, G.D. (2005) In: Cahn, R.W., Haasen, P. and Kramer, E.J., Eds., Materials Science and Technology, WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim, Vol. 4/5, 105.
- 15. Ukhin, N.A. (1972) FTP, 6, 931.
NOTES
*Corresponding author.






