Received 27 February 2015; accepted 27 June 2015; published 30 June 2015

ABSTRACT

It is shown that in the Earth’s atmosphere, due to influence of the gravitational field, coefficient of thermal expansion depends on altitude. The altitude intervals for individual gases for which the laws of ideal gases can be applied have been determined and it has been established that they are dependent on the adiabatic index and molar mass of these gases.

Keywords:

Ideal Gases, Inhomogeneous Medium, The Earth’s Atmosphere

1. Introduction

One of the fundamental laws of physics states that all characteristic properties of inhomogeneous (nonisotropic) medium must be inhomogeneous, in other words, they must depend on space coordinates. Until recently this principle was violated in relation speed of sound in the Earth’s atmosphere, which is one of most important thermodynamic parameter of medium. It was thought that the Earth’s gravitational field did not affect the processes of generating and propagation of sound waves and that is why the Earth’s atmosphere could be considered as a homogeneous medium in relation to sound waves. Proceeding from this assumption, sound spreads with adiabatic velocity, which is dependent only on temperature., i.e.. This circumstance can be mostly explained by the absence of experimental data concerning speed of sound measurement on different altitudes. It is proved by the fact that this kind of data is not given in a monograph-guide [1] , which is the official document of well-known American organizations like National Oceanic and Atmospheric Administration., National Aeronautics and Space Administration, United States Air Force. In the work [2] , it was shown that accounting of the inhomogeneity of the Earth’s atmosphere leads to arising of one more isobaric mechanism of generation and propagation of sound, and consequently, together with adiabatic, speed of sound possesses also isobaric speed 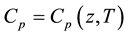and real sound speed is defined by these two speeds 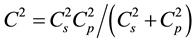and thus.

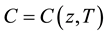The situation is absolutely similar in relation of thermal expansion coefficient for ideal gases. The first experiments that were supposed to determine this coefficient were conducted by G. Amontons (1661-1703) at the end of XVII century. Then this problem was studied by the outstanding scientists like Robert Boyle, Alessandro Volta, John Dalton, Joseph Priestley, Nicolas-Theodore de Saussure, Jacques Charles and others. The considerable contribution in the determination of coefficient was done by the great French scientist Joseph Luis Gay-Lussac (1778-1850). The results of experiments conducted by these scholars can be briefly defined as follows:

*At identical increasing of temperature, all the ideal gases are expanded identically.

*At constant pressure, volume of ideal gas linearly depends on temperature t˚C.

(1.1)

where 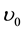is gas volume at which 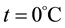and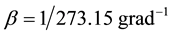―is the coefficient of thermal expansion. After Kelvin had introduced absolute temperature scale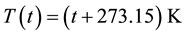, volume’s dependence on temperature in the case of isobaric process looks like:

(1.2)

and it is called Gay-Lussac’s Law.

It is obvious that those experiments were conducted in the normal conditions, in other words, at a temperature of 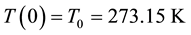and under a pressure of. Experiments, for defining the dependence 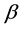on altitude, had not been conducted. Consequently, according to Gay-Lussac’s law it is accepted that at any altitude of the earth’s atmosphere, where is the initial temperature of air [3] -[5] . Such definition of must be theoretically proved, since coefficient of thermal expansion is the same characteristic of air as speed of sound and for this reason in the Earth’s atmosphere it must depend as on the initial temperature T as well as on altitude z i.e.. This article is concerned with the determination of this dependence.

2. Adiabaticity of Atmosphere of the Earth

It is known that the Earth’s atmosphere represents multilayered structure and in each layer, dependences of physical parameters on geometrical altitude z are different. The chart in Pic. 1 which is given in the monograph- guide [1] , and can be found in internet [6] as well as in the scientific literature [7] [8] shows that in the interval of altitudes from to (troposphere) temperature reduces under strictly linear law . In the interval of altitudes from to (tropopause) it is constant, in the interval from to (stratosphere) it increases and then up to (mesosphere) it decreases again approximately by law of.

Such sharp deviation from dynamics of temperature change in the tropopause and stratosphere means that some anomalous process develops there as a result of which thermal energy is absorbed and thus medium is not adiabatic. So, we suppose that the atmosphere is adiabatic only in the troposphere, where temperature decreases according strictly to the linear law and in which entropy s satisfy the adiabatic equation.

(2.1)

Here t is time, is medium’s movement velocity. We also think that the troposphere is non-dissipative and inhomogeneous medium. For such medium our theory is true, and it was considered in the research [2] according to which sound possesses two speeds:

adiabatic speed― (2.2)

isobaric speed― (2.3)

Here, is thermal capacitance at constant pressure, and are stationary values (equilibrium value) of pressure and density. Considering that the air is an ideal gas and dependence between pressure and density in adiabatic process is defined by the following relation:

(2.4)

from (2.2) for adiabatic speed of sound the following expression is derived:

(2.5)

Here, and are initial stationary values of pressure and density, adiabatic index is ratio of thermal capacities (specific heath) for air in the conditions of constant pressure and volume respectively,―is the mass of one molecule of atmospheric air,―is Boltsman constant, is the gas constant and -is mass of one mol air. Substituting Laplace’s barometric formula for an ideal gas

(2.6)

in expression (2.3) for isobaric speed of sound we obtain

(2.7)

Let’s define the altitude on which. From (2.5) and (2.7), it can be seen, that it is defined from a relation [2]

(2.8)

If we insert values of constant in (2.8) and select values of temperature and acceleration of gravity from the tables in the monograph-guide [1] for altitude of (and), we will obtain. For the same values of quantities formulae (2.5) and (2.7) give . As we see the altitude calculated by means of formula (2.8), at which adiabatic and isobaric speeds of sound are practically equal, it is very close to the upper boundary of troposphere who is determined by the graph (Figure 1) and to a high accuracy coincides with the altitude taken from the table of the monograph-guide [1] which proves high reliability of our results. Thus, the upper boundary of troposphere is determined by the condition. We assume that in case of fulfillment of this condition there occurs a resonance phenomenon stimulatory absorption of external energy due to which temperature in the tropopause remains constant while in the stratosphere it increases. Experimental verification of this hypothesis can also be considered as a significant discovery.

3. The Coefficient of Thermal Expansion in the Earth’s Atmosphere

Let’s show that isobaric sound speed (2.3) can be expressed by coefficient of thermal expansion, for that transform the expression

(3.1)

where―is the coefficient of thermal expansion. Thus, from formula (2.3) we obtain for

(3.2)

If we compare the formula (3.2) with the formula (2.7) for the coefficient of air expansion we can find

(3.3)

From (3.3), it is clear that actually. But on the other hand if i.e. on the sea level when the air is heated, it is not expanded. The absurdity of this result is obvious, but it doesn’t mean that the formula (3.3) has no physical meaning. In order to prove this let’s calculate changes in the altitude interval where is the troposphere’s upper boarder, which is determined by the condition and within this boundary our theory is true. According to the chart from the monograph-guide [1] we find and then

The change on the 1 m altitude will be. Thus, depends on altitude very weakly and that’s why it can be averaged over z. In order to do it let’s express first and through the adiabatic index. Using known relation from the formulas (2.8) and (3.3) it is easy to find:

(3.4)

(3.5)

Let’s average now in the altitude interval where and ε is dimensionless para- meter determining maximal altitude in the Earth’s atmosphere for which Gay-Lussac’s Law is performed i.e.

(3.6)

Simple calculations for average meaning give us:

(3.7)

According to Gay-Lussac’s Law it must be demanded:

(3.8)

The expression (3.8) has an important physical meaning, for it shows that for different gases the parameter and correspondingly an altitude, above which Gay-Lussac’s Law doesn’t work, have different meanings

(3.9)

In Table 1, there are presented values of and for different gases according to growth of their molar mass, where for every gas denotes altitude where if the Earth’s atmosphere was composed only of that gas. We’d like to note that for air the temperature value was taken according to altitude from the table of the monograph-guide [1] As there is no such table for other gases, instead of T in the formulas (3.4.) and (3.9) we take its average value all over the troposphere and according to the same chart it equals.

Analysis of Table 1 permits us to make the following conclusions:

1) For the gases whose number of atoms, the inequality is fulfilled. It means that these gases follow Gay-Lussac’s Law all over the interval. According to above offered hypothesis in the altitude interval medium adiabaticity is violated altogether and our theory is not true.

2) For the gases whose number of atoms the inequality is fulfilled. It means that these gases follow Gay-Lussac’s Law only in the interval. In the altitude interval medium is adiabatic, but Gay-Lussac’s Law not performed.

3) As the molar mass of gas increases, altitude decreases below of which Gay-Lussac’s Law is fulfilled. It can be explained by the fact that the more is the molar mass of gas the more is the influence of the Earth’s gravitational field and the more qualities of gas pass off from the ideal one.

It is interesting to determine an average value of thermal expansion coefficient for the case 2) in the interval. The simple calculation by means of the formulas (3.4), (3.5) and (3.9) give us:

(3.10)

As we can see, the influence of the gravitational field on polyatomic gases is revealed not only in the fact that, but also in the fact that in the altitude range their coefficient of thermal expansion is more than usual by value.

4. Conclusions

The paper demonstrates that the commonly held opinion on universality of the laws of ideal gas that has existed in science for more than two centuries is erroneous. These laws were discovered by means of experiments carried out at the sea level where the Earth atmosphere can be considered homogeneous medium [2] [9] . The effect of gravitational field of the Earth, which making notable the influence on thermodynamic properties of gases depending on their molar mass and indicator of adiabatic index, becomes more evident with increase of altitude. Our results are based on the assumption that all gases discussed in this work at sufficient approximation can be considered as ideal ones. Practically, all the gases are ideal especially in the upper layers of the atmosphere, since the formula (3.9) has meaning only when. Proceeding from this consideration we think, that distribution of densities of all gases in the Earth’s gravitational field follows Laplasse’s barometric formula (2.6) and the upper border, up to which medium’s adiabaticity is retained, can be defined from the condition.

We have shown that for the air this altitude coincides with the upper border of troposphere and at temperature in this altitude, which is taken from the table in monograph-guide [1] , condition is fulfilled with exact precision. It testifies the reliability of our theory and its results. For different gases altitude will be different, but they will share the fact that up to this altitude adiabatic speed of sound in them is less than isobaric speed or in other words, the compressibility of medium prevails over the incompressibility of it [9] .

At higher altitude where our theory is not true, we suppose that an inequality sign between and changes into an opposite and consequently, the change of medium properties from compressibility to incompressibility takes place. Thus, altitude in the Earth’s gravitational field is like Rubicon―when it is crossed, the properties of medium change into the opposite. On this bases we think that at this altitude, when, some anomalous, resonant processes occur and they are connected with absorption of thermal energy (for example, infrared solar radiation). It is clearly visible by the example of tropopause (Figure 1), where falling the air temperature suddenly stops and during the whole tropopause remains constant while in the stratosphere it increases.

The results of the work and considerations expressed herein are of fundamental importance for theoretical and applied physics and therefore require experimental verification. If the experiments prove correctness of our theoretical conclusions, this will lay the foundation to qualitatively new research in gasdynamics on the whole, as well as in physics of atmosphere in particular.

References