Journal of Modern Physics
Vol.06 No.08(2015), Article ID:58205,21 pages
10.4236/jmp.2015.68116
Fibre-Reinforced Generalized Thermoelastic Medium Subjected to Gravity Field
Fatimah S. Bayones1, Nahed S. Hussien1,2
1Mathematics Department, Faculty of Science, Taif University, Taif, Saudi Arabia
2Mathematics Department, Faculty of Science, Cairo University, Cairo, Egypt
Email: f.s.bayones@hotmail.com, hussein.nahed@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 February 2015; accepted 20 July 2015; published 23 July 2015
ABSTRACT
The present paper is aimed at studying the effects of thermal relaxation time and gravity of a two- dimensional problem with anisotropic semi-infinite solid media with the deformation of fiber- reinforced generalized thermoplastic. The harmonic function techniques are used. The thermal stresses, temperature and displacement have been obtained. These expressions are calculated numerically for two values of elastic constants for mediums M1 and M2 respectively. The results obtained are displayed by graphs to clear the phenomena physical meaning. The results indicate that the effect of gravity, relaxation times and parameters of fibre-reinforced of the material medium are very pronounced.
Keywords:
Fibre-Reinforced Medium, Thermal Relaxations, Viscosity, Thermoelastic, Gravity

1. Introduction
The classical theory of thermoelasticity has been generalized and modified into various thermoelastic models that run under the label of “hyperbolic thermoelasticity”. The linear theory of elasticity of paramount importance in the stress analysis of steel is the commonest engineering structural material. To a lesser extent, linear elasticity describes the mechanical behavior of the other common solid materials, e.g. concrete, wood and coal. Thermoelasticity theories, which admit a finite speed for thermal signals, have been receiving a lot of attention for the past four decades. In contrast to the conventional coupled thermoelasticity theory based on a parabolic heat equation, Biot [1] , which predicts an infinite speed for the propagation of heat, these theories involve a hyperbolic heat equation and are referred to as generalized thermoelasticity theories.
The notation hyperbolic reflects the fact that thermal waves are modelled, avoiding the physical paradox of the infinite propagation speed of the classical model. At present, there are several theories of the hyperbolic thermoelasticity. The first was developed by Lord and Shulman [2] who obtained a wave-type heat equation by postulating a new law of heat conduction to replace the classical Fourier’s law. This new law contains the heat flux vector as well as its time derivative. It also contains a new constant that acts as a relaxation time. The second was developed by Green and Lindsay [3] . Tanaka, et al. [4] studied the application of boundary element method to 3-D problems of coupled thermoelasticity. A generalization of this inequality was proposed by Green and Laws [5] . Abd-Alla, et al. [6] discussed the transient thermal stresses in atransversely isotropic infinite circular cylinder. Effect of initial stress on generalized thermoelastic problem in an infinite circular cylinder is discussed by El-Naggar and Abd-Alla [7] . Effect of the rotation on an infinite generalized magneto-thermoelastic diffusion body with a spherical cavity was discussed by Abd-Alla, et al. [8] . Ezzat and Youssef [9] studied the generalized magneto-thermoelasticity in a perfectly conducting medium. Abd-Alla and Bayones [10] studied effect of rotation and initial stress on generalized-thermoelastic problem in an infinite circular cylinder. Dai and Wang [11] studied the magneto-elastodynamic stress and perturbation of magnetic field vector in an orthotropic laminated hollow cylinder. Abd-Alla, et al. [12] studied thermal stresses in a non-homogeneous orthotropic elastic multilayered cylinder.
Fibre-reinforced composites are used in a variety of structures due to their low weight and high strength. A continuum model is used to explain the mechanical properties of such materials. Craig and Hart [13] studied the stress boundary value problem for finite plane deformation of a fibre-reinforced material. Sengupta and Nath [14] discussed the problem of surface waves in a fibre-reinforced anisotropic elastic media. Singh and Singh [15] discussed the reflection of plane waves at the free surface of a fibre-reinforced elastic half-space. Singh [16] discussed the wave propagation in an incompressible transversely isotropic fibre-reinforced elastic media. Singh [17] studied the effects of anisotropy on reflection coefficients of plane waves in fibre-reinforced thermoelastic solid. Kumar and Gupta [18] investigated a source problem in fibre-reinforced anisotropic generalized thermoelastic solid under acoustic fluid layer. Alla et al. [19] investigated propagation of Rayleigh waves in generalized magneto-thermoplastic orthotropic material under initial stress and gravity field. Thermal stresses in an infinite circular cylinder have been investigated by Abd-Alla et al. [20] . Abd-Alla and Mahmoud [21] studied the magneto-thermoelastic problem in rotatin non-homogeneous orthotropic hollow cylinder under the hyperbolic heat conduction model. Abd-Alla and Ahmed [22] investigated the Rayleigh waves in an orthotropic thermoelastic medium under gravity field and initial stress. Rayleigh waves in a magnetoelastic half-space of orthotropic material under the influence of initial stress and gravity field were investigated by Abd-Alla et al. [23] . Elnaggar and Abd-Alla [24] studied Rayleigh waves in magneto-thermo-microelastic half-space under initial stress. Abd-Alla and Ahmed [25] discussed Rayleigh waves in an orthotropic thermoelastic medium under gravity field and initial stress. Effect of rotation and initial stress on an infinite generalized magneto-thermoelastic diffusion body with a spherical cavity is investigated by Abd-Alla and Abo-Dahab [26] .
In this paper then we study the effect of thermal relaxation time and gravity on anisotropic semi-infinite solids with the deformation of fibre-reinforced generalized thermoelastic. The thermal stresses, temperature and displacement have been obtained. Furthermore, the displacement, temperature and stresses are computed numerically in each of these cases and illustrated graphically. The results indicate that the effect of thermal relaxation time and gravity on the thermal stresses, temperature and displacement are very pronounced.
2. Formulation of the Problem
Consider a homogeneous thermally conducting transversely fibre-reinforced medium with thermal relaxation time and gravity. Let us consider a system of anisotropic Cartesian axes Oxyz,
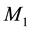 and
and
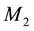 be two fires- reinforced elastic anisotropic semi-infinite solid media. Let O be the any point on the plane boundary and Oz points vertically downward to the medium
be two fires- reinforced elastic anisotropic semi-infinite solid media. Let O be the any point on the plane boundary and Oz points vertically downward to the medium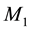 . Further the mechanical properties of
. Further the mechanical properties of
 are different from those of
are different from those of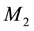 . These media extend to an infinite great distance from the origin and are separated by a plane horizontal boundary and
. These media extend to an infinite great distance from the origin and are separated by a plane horizontal boundary and
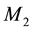 is to be taken above
is to be taken above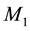 . Further let us assume that
. Further let us assume that
 are the components of displacements at any point
are the components of displacements at any point
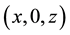 at any time t. It is also assumed that gravitational field produces a hydrostatic initial stress is produced by a slow process of creep where the shearing stresses tend to become smaller or vanish after a long period of time.
at any time t. It is also assumed that gravitational field produces a hydrostatic initial stress is produced by a slow process of creep where the shearing stresses tend to become smaller or vanish after a long period of time.
The equilibrium conditions of the initial stress field [20]
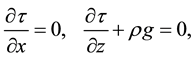 (1)
(1)
The stress-temperature equation is given by [21] :
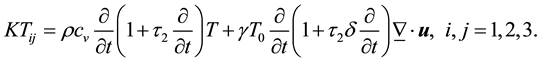 (2)
(2)
The dynamical equations of motion for three-dimensional elastic solid medium under the influence of initial stress and gravity [22]
 (3)
(3)
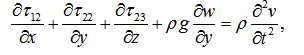 (4)
(4)
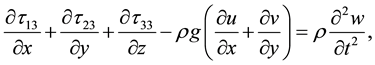 (5)
(5)
The constitutive equations for a fibre-reinforced linearly thermoelastic anisotropic medium with respect to a preferred direction
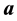 are [23]
are [23]
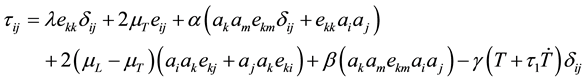 (6)
(6)
where












reinforced anisotropic elastic parameters;



Introducing Equations (7) into Equations (3)-(5), we have



By Helmholtz’s theorem [24] , the displacement vector




which reduces to

Now using (12) in (8) and (9) we obtain the following wave equation in




Substituting from Equation (12) into Equation (2), we obtain:

where,


3. Solution of the Problem
Assuming a simple harmonic time dependent factor for all the quantities and omitting the factor


Using Equations (17) in (13)-(16), we get a set of differential equations for medium M1 as follows:




where
and those for the medium





where
Eliminating the temperature


Using Equation (19) and Equation (26), we get

Equations (22)-(25) tend to the solutions



where the constants





From Equations (28) and (29) in Equation (18), we get

where,



Since the displacement at





Finally from Equation (17), we have




From Equations (39)-(42), we have


And the stress components are






And for medium


And the stress components are






4. Boundary Conditions
The boundary conditions for the titled problem are:
(1) The displacement components at the boundary surface between the media M1 and M2 must be continued at all times and positions.
i.e.

(2) The stress components t31, t32 and t33 must be continuous at the boundary z = 0.
i.e.
(3) The thermal boundary conditions must be continuous at the boundary z = 0.
i.e.
Applying the boundary conditions (1)-(3), we have








From Equations (53) and (56), we have

The discussion in two fibre-reinforced anisotropic solid thermoelastic under effect thermal relaxation time and gravity is clear up from Figures 1-4 and dissection some special cases is clear up from Figures 5-12.
5. Particular Cases
5.1. Isotropic Generalized Thermoelastic Medium with Gravity
In this case, substituting


5.2. Fibre-Reinforced Anisotropic Generalized Thermoelastic Medium with Neglected the Gravity .
In this case, letting g = 0, in Equations (47)-(51), we obtain the corresponding expressions of displacement, temperature and stress in anisotropic generalized thermoelastic medium with neglected the gravity.
5.3. Isotropic Generalized Thermoelastic Medium with Neglected the Gravity
In this case, substituting



6. Numerical Results and Discussion
The following values of elastic constants are considered Singh [25] and Chattopadhyay [26] , for mediums


The numerical technique outlined above was used to obtain the displacement, temperature and thermal stresses under effect of thermal relaxation time and gravity. These distributions are shown in Figures 1-12 respectively.
-In two fibre-reinforced anisotropic solid thermoelastic under effect thermal relaxation time and gravity
From Figure 1: For medium




Figure 1. Effects of g on displacements u, w, temperature T and thermal stresses with horizontal distance z for medium
From Figure 2: For medium





From Figure 3: For medium M1 it is seen that the displacements, temperature, normal stresses

Figure 2. Effects of g on displacements u, w, temperature T and thermal stresses with horizontal distance z for medium M2. --- --- ---- g = 0.1, _______ g = 0.3, …………. g = 0.5.
shear stress



From Figure 4: For medium






Figure 3. Effects of




Figure 4. Effects of




Figure 5. Effects of g on displacements u, w, temperature T and thermal stresses with horizontal distance z for medium M1. --- --- ---- g = 0.1, _______ g = 0.3, …………. g = 0.5.
-In two fibre-reinforced isotropic solid thermoelastic under effect thermal relaxation time and gravity
From Figure 5: For medium



Figure 6. Effects of g on displacements u, w, temperature T and thermal stresses with horizontal distance z for medium M2. --- --- ---- g = 0.1, _______ g = 0.3, …………. g = 0.5.
shear stress


From Figure 6: For medium





From Figure 7: For medium






From Figure 8: For medium


Figure 7. Effects of




and shear stress



-In two fibre-reinforced anisotropic generalized thermoelastic medium with neglected the gravity
From Figure 9: For medium


Figure 8. Effects of





shear stress




Figure 9. Effects of





Figure 10. Effects of





Figure 11. Effects of





Figure 12. Effects of





From Figure 10: For medium






-In two fibre-reinforced isotropic generalized thermoelastic medium with neglected the gravity
From Figure 11: For medium






From Figure 12: For medium






7. Conclusions
Due to the complicated nature of the governing equations of the generalized thermoelasticity fiber-reinforced theory, the work done in this field is unfortunately limited in number. The method used in this study provides a quite successful in dealing with such problems. This method gives exact solutions in the generalized thermoelastic medium without any assumed restrictions on the actual physical quantities that appear in the governing equations of the problem considered. Important phenomena are observed in all these computations:
・ It was found that for large values of relaxation time they give close results. The solutions obtained in the context of generalized thermoelasticity theory, however, exhibit the behavior of the components of displacement, stresses and temperature.
・ By comparing Figures 1-12, it was found that the surface wave velocity has the same behavior in both media. But with the passage of relaxation times and gravity, numerical values of the components of displacement, stresses and temperature in the thermoelastic medium are large in comparison due to the influences of gravity and relaxation times.
・ Special cases are considered as isotropic generalized thermoelastic medium with gravity and fibre-reinforced anisotropic generalized thermoelastic medium with neglected the gravity in anisotropic generalized thermoelastic medium, as well in the isotropic case.
・ The results presented in this paper should prove useful for researchers in material science, designers of new materials.
・ Study of the phenomenon of rotation and gravity is also used to improve the conditions of oil extractions.
Cite this paper
Fatimah S.Bayones,Nahed S.Hussien, (2015) Fibre-Reinforced Generalized Thermoelastic Medium Subjected to Gravity Field. Journal of Modern Physics,06,1113-1134. doi: 10.4236/jmp.2015.68116
References
- 1. Biot, M.A. (1956) Journal of Applied Physics, 27, 240-253. http://dx.doi.org/10.1063/1.1722351
- 2. Lord, H. and Shulman, Y. (1967) Journal of the Mechanics and Physics of Solids, 15, 299-309.
http://dx.doi.org/10.1016/0022-5096(67)90024-5 - 3. Green, A.E. and Lindsay, K.A. (1972) Journal of Elasticity, 2, 1-7.
http://dx.doi.org/10.1007/BF00045689 - 4. Tanaka, M., Matsumoto, M. and Moradi, M. (1995) Engineering Analysis with Boundary Element, 16, 297-303. http://dx.doi.org/10.1016/0955-7997(95)00074-7
- 5. Green, A.E. and Laws, N. (1972) Archives of Rational Mechanics and Analysis, 45, 45-47.
http://dx.doi.org/10.1007/BF00253395 - 6. Abd-Alla, A.M., Abd-Alla, A.N. and Zeidan, N.A. (2001) Applied Mathematics and Computation, 121, 93-122. http://dx.doi.org/10.1016/S0096-3003(99)00265-9
- 7. El-Naggar, A.M. and Abd-Alla, A.M. (1987) Earths, Moon Planets, 37, 213-223.
http://dx.doi.org/10.1007/BF00116637 - 8. Abd-Alla, A.M., Abo-Bahab, S.M. and Bayones, F.S. (2011) International Review of Physics, 5, 171-181.
- 9. Ezzat, M.A. and Youssef, H.M. (2005) International Journal of Solids and Structures, 42, 6319-6334.
http://dx.doi.org/10.1016/j.ijsolstr.2005.03.065 - 10. Abd-Alla, A.M. and Bayones, F.S. (2011) Applied Mathematical Sciences, 5, 2049-2076.
- 11. Dai, H.L. and Wang, X. (2006) International Journal of Engineering Science, 44, 365-378.
http://dx.doi.org/10.1016/j.ijengsci.2005.12.008 - 12. Abd-Alla, A.M., Abd-Alla, A.N. and Zeidan, N.A. (2000) Journal of Thermal Stresses, 23, 413-428.
http://dx.doi.org/10.1080/014957300403914 - 13. Craig, M.S. and Hart, V.G. (1979) Quarterly Journal of Mechanics and Applied Mathematics, 4, 473-498.
http://dx.doi.org/10.1093/qjmam/32.4.473 - 14. Sengupta, P.R. and Nath, S. (2001) Sadhana, 26, 363-370. http://dx.doi.org/10.1007/BF02703405
- 15. Singh, B. and Singh, S.J. (2004) Sadhana, 29, 249-257. http://dx.doi.org/10.1007/BF02703774
- 16. Singh, B. (2007) Archives of Applied Mechanics, 77, 253-258.
http://dx.doi.org/10.1007/s00419-006-0094-9 - 17. Singh, B. (2007) International Journal of Mechanics and Solids, 2, 39-49.
- 18. Kumar, R. and Gupta, R. (2009) Multidiscipline Modeling in Materials and Structures, 5, 283-288.
http://dx.doi.org/10.1163/157361109789017014 - 19. Abd-Alla, A.M., Abo-Dahab, S.M. and Hammad, H.A.H. (2011) Applied Mathematical Modelling, 35, 2981-3000. http://dx.doi.org/10.1016/j.apm.2010.11.067
- 20. Abd-Alla, A.M., Yahya, G.A. and Farhan, A.M. (2012) Journal of Mechanical Science and Technology, 26, 1829-1839. http://dx.doi.org/10.1007/s12206-012-0424-5
- 21. Abd-Alla, A.M. and Mahmoud, S.R. (2010) Meccanica, 45, 451-462.
http://dx.doi.org/10.1007/s11012-009-9261-8 - 22. Abd-Alla, A.M. and Ahmed, S.M. (1996) Earth, Moon, and Planets, 75, 185-197.
http://dx.doi.org/10.1007/BF02592996 - 23. Abd-Alla, A.M., Hammad, H.A.H. and Abo-Dahab, S.M. (2004) Applied Mathematics and Computation, 154, 583-597. http://dx.doi.org/10.1016/S0096-3003(03)00767-7
- 24. Elnaggar A.M. and Abd-Alla, A.M. (1989) Earth, Moon, and Planets, 45, 175-185.
http://dx.doi.org/10.1007/BF00055784 - 25. Abd-Alla, A.M. and Ahmed, S.M. (1996) Earth, Moon, and Planets, 75, 185-197.
http://dx.doi.org/10.1007/BF02592996 - 26. Abd-Alla, A.M. and Abo-Dahab, S.M. (2012) Journal of Thermal Stresses, 35, 892-912.7.23 http://dx.doi.org/10.1080/01495739.2012.720209






















