Journal of Modern Physics
Vol.06 No.04(2015), Article ID:55004,4 pages
10.4236/jmp.2015.64048
Zero Point Energy Effects on Quantum Electrodynamics
Bo Lehnert
Alfvén Laboratory, Royal Institute of Technology, Stockholm, Sweden
Email: bo.lehnert@ee.kth.se
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 January 2015; accepted 21 March 2015; published 25 March 2015
ABSTRACT
The vacuum is not a state of empty space, but is populated by electromagnetic fluctuations at a lowest nonzero level, the Zero Point Energy (ZPE). As distinguished from conventional theories, such as that of the Standard Model, the present revised quantum electrodynamic theory (RQED) includes the ZPE in its field equations. This leads to new results far beyond those obtained from conventional theories such as those by Dirac and Higgs. Thus, the present theory results in massive elementary particles from the beginning, being independent of the theory by Higgs. This paper describes the background and results of RQED, summarizing the weak points of conventional theories, the unification of included fundamental concepts, the present basic field equations, new obtained results, and special points of experimental support. In other words, the new points stressed in this paper are in particular the relation between a nonzero electric field divergence in the vacuum and the ZPE, and a number of new experimentally supported results due to a nonzero ZPE energy density in the same state.
Keywords:
Zero Point Energy, Quantum Electrodynamics, Standard Model and Beyond

1. Introduction
The vacuum is not merely a state of empty space. The first indication of this fact was already given in con- nection with Planck’s theory of radiation. Thus, the average energy of an oscillator in thermal equilibrium also has to include a lowest nonzero energy level of one-half quantum per state, i.e. the Zero Point Energy (ZPE).
Conventional theories, such as that of the Standard Model of elementary particles, are on the other hand based on a vacuum state of empty space. The related electromagnetic field equations are then of the reduced Hertz type, being a special case of those by Maxwell, i.e. without source terms in the form of conduction currents and free charges. This comes out to impose a severe restriction on the solutions.
To meet the requirement of a vacuum state which includes effects due to the Zero Point Energy and related sources, a revised quantum electrodynamic approach (RQED) has been made by the author, as described in a succession of investigations [1] -[4] . For detailed deductions, a reference is made to the latter. This paper mainly elucidates the background and aspects of the present theory, in a discussion of the weak points of the conven- tional theories, the unification of fundamental concepts into the present approach, its basic field equations, new results obtained beyond those of conventional theories such as by Dirac and Higgs, and points of experimental support.
2. Weak Points of Conventional Theories
The treatment of the vacuum as an empty space leads to a number of shortcomings of the conventional theories on which the following points can be made:
・ The rest mass is missing in the models of elementary particles, in contradiction with experiments. In making this point clear, P. W. Higgs and F. Englert become well worth their honours of distinction.
・ The theory by Higgs [5] is based on a spontaneous nonlinear mechanism of symmetry breaking of an empty vacuum state, by which an unstable boson of unspecified but large rest mass is being formed. In its turn, this particle then decays into a set of lighter and massive elementary particles. Thereby the absolute value of the rest mass of the Higgs particle is not obtained from the theory. It may further be questioned how this two- stage process will function in reality, and how one single unstable boson of large mass can give rise to all other elementary particles through this decay process.
・ The Standard Model is unable to explain that charged leptons do not “explode” under the action of their electrostatic eigenforce.
・ In an empty vacuum state the quantized solutions for electromagnetic waves lead to a vanishing integrated spin of a photon model, in contradiction with observations. This is even the case when there are local contri- butions to a spin, but which cancel after integration.
・ Conventional theory further leads to restricted photon models which cannot explain the experimentally con- firmed needle radiation and the photoelectric effect.
3. Present Revised Quantum Electrodynamic Theory
3.1. A Unification of Fundamental Concepts
The present RQED theory includes and combines a number of earlier established fundamental concepts:
・ The Zero Point Energy reveals itself as quantum fluctuations, part of which also carry electric charge as pointed out by Abbott [6] . An example has been given by Casimir [7] who predicted that there arises an attractive force between two parallel metal plates in the vacuum. This force was first confirmed experimen- tally by Lamoreaux [8] . Thus, the ZPE gives rise to a “photon gas” having a physically real macroscopic pre- ssure and energy density.
・ The ZPE effects can be included in the electromagnetic vacuum field equations, by an additional source term. To preserve the Lorentz and gauge invariance, this term has the form of a four-dimensional current density which contains a nonzero electrical charge density  due to a nonzero electric field divergence. As demonstrated in the following subsection, this leads in its turn to revised field equations being different from those by Higgs, and which are characterized by intrinsic linear broken symmetry.
due to a nonzero electric field divergence. As demonstrated in the following subsection, this leads in its turn to revised field equations being different from those by Higgs, and which are characterized by intrinsic linear broken symmetry.
・ There is thus a direct connection between a nonzero ZPE and a nonzero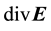 . The latter reveals itself in local electrically charged as well as electrically neutral electromagnetic fluctuations, in spatially integrated configurations of net as well as vanishing electric charge, and in configurations of integrated total energy and mass.
. The latter reveals itself in local electrically charged as well as electrically neutral electromagnetic fluctuations, in spatially integrated configurations of net as well as vanishing electric charge, and in configurations of integrated total energy and mass.
・ The Lorentz invariance of Special Relativity by Einstein includes a four-dimensional current density in the vacuum of the present theory. The resulting equations do not only apply to plane waves, but also to three- dimensional geometry such as to cylindrical waves. As shown in the following subsection, this results in an extended form of Lorentz invariance, in which the velocity c of light appears in the form of a velocity vector C having the modulus c.
・ As demonstrated by Schiff [9] among others, the field equations are used as a guideline for interpretation of quantum electromagnetic theory. In the present approach a short-cut can therefore be made by first deter- mining the general solutions of the field equations, and then imposing relevant quantum conditions. This is justified by the fact that the quantized equations become identical with the original equations in which the potentials and current densities are merely being replaced by their expectation values, as shown by Heitler [10] . This should therefore be not too far from the truth, i.e. by using the most probable trajectories and states in a first approximation.
3.2. Basic Field Equations of Present Theory
According to earlier deductions [1] - [4] , the present RQED theory unifies the described fundamental concepts in a Lorentz and gauge invariant form. This includes corresponding solutions for particle models representing matter as well as antimatter, in a way being analogous to the theory by Dirac. For a three-dimensional represen- tation these extended field equations in the vacuum become
 (1)
(1)
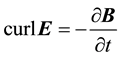 (2)
(2)
 (3)
(3)
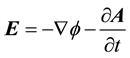 (4)
(4)
 (5)
(5)
for the electric and magnetic field strengths E and B, the electrostatic and magnetic vector potentials 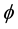 and A, and the velocity vector C where
and A, and the velocity vector C where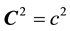 . The nonzero ZPE vacuum effects are represented by the first term in the right-hand member of Equation (1), in the form of a nonzero space-charge current density, as well as by the nonzero local charge density of Equation (5).
. The nonzero ZPE vacuum effects are represented by the first term in the right-hand member of Equation (1), in the form of a nonzero space-charge current density, as well as by the nonzero local charge density of Equation (5).
3.3. New Results Obtained from Present Theory
From this revised theory a number of new results are obtained beyond those emerging from conventional theory. The following points can here be made on steady particle states:
・ The source term of Equation (1) gives rise to steady electromagnetic states, not being present in conventional theory. One of the consequences of this is that the corresponding particle models are supplied with a rest mass already from the beginning, and independently of the decay process in the theory by Higgs.
・ A model of the Z boson can be deduced from the present theory, having an effective radius of about 10?18 m, in agreement with measured data given by Quigg [11] among others.
・ The revised theory further yields a model of the at CERN detected Higgs-like particle [12] [13] . This model possesses all the experimentally confirmed properties, such as a vanishing charge and spin, an unstable behaviour, and a mass of 125 GeV for an effective radial dimension of about 10?18 m. The obtained relation between mass and effective radius does not come out from the theory by Higgs.
・ The proposed decay of the Higgs boson into two Z bosons further initiates the idea of superimposing two Z bosons to form a model of such a particle. The resulting composite solution of the present theory is thereby consistent with the point made by Quigg [11] , namely that the Higgs-like boson is perhaps not a truly ele- mentary particle but is built out of as yet unobserved constituents.
・ The source term in Equation (1) generates a magnetic contribution in a model of the electron, by which a corresponding force counteracts the electrostatic expansive force due to the net charge.
・ The lepton models with net charge are associated with radially divergent solutions and shrinking radial dimensions. By means of a revised renormalization procedure, finite values of the charge, magnetic moment, mass, and spin can still be obtained. A variational analysis then yields a deduced value of the elementary charge “e” which is localized to a narrow “channel” being centred around the experimental value of e, having a width of only a few percent of e.
・ The present theory is also applicable to particle models with vanishing net charge, such as the neutrino.
・ The obtained lepton models further embrace a new concept in the form of considerable local intrinsic electric charges of both polarities. These charges are sometimes an order of magnitude larger than the net electronic charge. If this would also come out to be the case for quarks, the corresponding electrostatic interactions may become comparable to that of the strong force. This point requires further investigation.
Concerning propagating electromagnetic waves, the following points should be observed:
・ With the present revised field equations, the wave-particle dualism becomes an intrinsic property of the solu- tions. A physically relevant model of the individual photon thereby has to satisfy the properties of a wave or a wave packet of preserved and spatially limited geometry which propagates in an undamped manner in a specified spatial direction. A proper individual photon model has therefore to be reconcilable with cylindrical waves with small radial dimensions, a nonzero spin, and an associated very small but nonzero rest mass, as being determined by the Lorentz invariance which is extended to cylindrical geometry. This rest mass arises at the expense of a very small reduction of the phase and group velocities from the value c. Such a reduction occurs first in the tenth decimal of c.
・ The individual photon model also makes possible a behaviour both as a particle in the shape of needle radi- ation, and as a wave concept with interference phenomena. This contributes to the understanding of the photoelectric effect and of two-slit experiments.
・ The solutions of the present field equations also apply to hollow screw-shaped light beam geometry, in agreement with observations.
・ There are intrinsic local charges of both polarities also in the obtained photon models of propagating waves. This contributes to the understanding of electron-positron pair formation of an individual photon.
4. Experimental Support of Present Theory
From the deduced results direct experimental support of the present theory is seen to appear especially in the following cases:
・ An obtained rest mass of leptons agrees with experiments [1] [4] .
・ The Higgs-like particle detected at CERN can in all its fundamental properties be reproduced by the present theory. This also applies to the relation between the mass and the characteristic radius of the Z boson and this Higgs-like particle [1] [4] [14] [15] .
・ The charged leptons are prevented from “exploding” under the action of their electrostatic eigenforce [1] [4] [16] .
・ A deduced value is obtained for the elementary electronic charge being close to its experimentally deter- mined value [1] [4] [16] [17] .
・ The individual photon model achieves a nonzero spin, as confirmed by experiments [1] [4] .
・ The observed needle radiation comes out of the theory [1] [4] [18] .
5. Conclusions
The conventional theories which are based on the concept of a vacuum state of empty space lead to severely restricted forms of corresponding solutions. This limitation can be removed by the present revised quantum electrodynamic approach which is based on a vacuum state, including the Zero Point Energy. The resulting solutions reach far beyond those obtained from conventional theories, such as that of the Standard Model.
The future will confirm what is relevant and not relevant in these efforts.
References
- Lehnert, B. (2013) Revised Quantum Electrodynamics. In: Dvoegalzov, V.V., Ed., Nova Science Publishers, New York.
- Lehnert, B. (2008) Revised Quantum Electrodynamics. In: Shukla, P.K., Stenflo, L. and Eliasson, B., Eds., New Aspects of Plasma Physics, World Scientific Publishing, Singapore-Hackensack-London, 52.
- Lehnert, B. (2008) Wave-Particle Properties and Pair Formation of the Photon. In: Shukla, P.K., Stenflo, L. and Eliasson, B., Melville, Eds., Frontiers in Modern Plasma Physics, American Institute of Physics, New York, 282.
- Lehnert, B. (2014) Journal of Electromagnetic Analysis and Applications, 6, 319-327.
- Higgs, P.W. (1966) Physical Review, 145, 1156-1163. http://dx.doi.org/10.1103/PhysRev.145.1156
- Abbott, L. (1988) Scientific American, 258, 106-113. http://dx.doi.org/10.1038/scientificamerican0588-106
- Casimir, H.B.G. (1948) Proc. K. Ned. Akad .Wet., 51, 793-795.
- Lamoreaux, S.K. (1997) Physical Review Letters, 78, 5-8. http://dx.doi.org/10.1103/PhysRevLett.78.5
- Schiff, L. (1949) Quantum Mechanics. McGraw-Hill Book Comp., Inc., New York and London, Ch. XIV.
- Heitler, W. (1954) The Quantum Theory of Radiation. 3rd Edition, Clarendon Press, Oxford, 409.
- Quigg, C. (2008) Scientific American, 298, 46-53. http://dx.doi.org/10.1038/scientificamerican0208-46
- Aad, G., Abajyan, T., Abbott, B., Abdallah, J., Abdel Khalek, S., Abdelalim, A.A., et al. (2012) Physics Letters B, 716, 1-29. http://dx.doi.org/10.1016/j.physletb.2012.08.020
- Chatrchyan, S., Khachatryan, V., Sirunyan, A.M., Tumasyan, A., Adam, W., Aguilo, E., et al. (2002) Physics Letters B, 716, 30-61. http://dx.doi.org/10.1016/j.physletb.2012.08.021
- Lehnert, B. (2013) Progress in Physics, 4, 31-32.
- Lehnert, B. (2014) Progress in Physics, 10, 5-7.
- Lehnert, B. and Höök, J. (2010) Journal of Plasma Physics, 76, 419-428. http://dx.doi.org/10.1017/S0022377809990638
- Lehnert, B. and Scheffel, J. (2002) Physica Scripta, 65, 200-207. http://dx.doi.org/10.1238/Physica.Regular.065a00200
- Lehnert, B. (2011) International Review of Physics (IREPHY), 5, 15-18.

