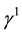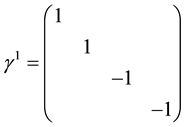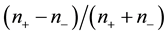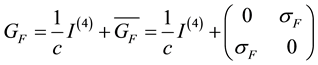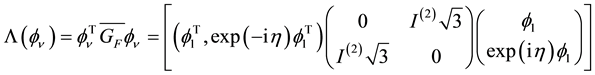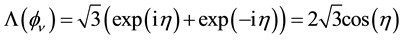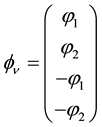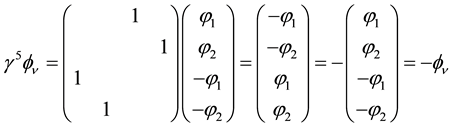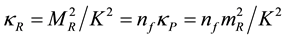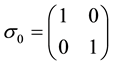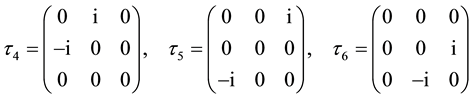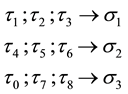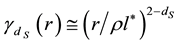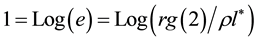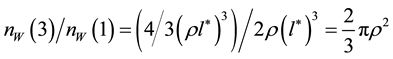Journal of Modern Physics
Vol.06 No.06(2015), Article ID:56655,17 pages
10.4236/jmp.2015.66086
Physics in Discrete Spaces: On the Standard Model of Particles
Pierre Peretto
Laboratory of Physics and Modelling of Condensed Matter, Grenoble, France
Email: Pierre.peretto@lpmmc.cnrs.fr
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 January 2015; accepted 23 May 2015; published 26 May 2015
ABSTRACT
We show that the model of discrete spaces that we have proposed in previous contributions gives a comprehensive and detailed interpretation of the properties of the standard model of particles. Moreover the model also suggests the possible existence of a non-standard family of particles.
Keywords:
Standard Model of Particles, Chirality, Regge Trajectories, CKM Matrix

1. Introduction
According to the model of discrete space-time that we have put forward in preceding contributions, the universe as a whole could be considered as a sort of spin glass that is a set of randomly interacting Ising spins called cosmic bits. This model accounts for several fundamental properties of the physical world, such as the structure of space-time [1] , the postulates of quantum theory [2] , and the fundamental interactions (gravitation included) [3] . To be convinced that, the model provides a general description of natural phenomena, but something essential is still missing: it must explain the properties of matter itself that is it must provide an interpretation to the standard model of particles. Usual theories of natural phenomena appeal to the concept of mathematical points that are systems deprived of the possibility of housing such complex structures as elementary particles. The model of discrete space-time offers this possibility because, in a discrete space, a physical point, called a world point, has a finite physical size. A discrete space-time model so allows an internal organization to develop inside world points, providing a way for the building of complex structures. This is the object of the present contribution.
2. The Group S4 and the Organization of Elementary Particles
2.1. Structure of Elementary Particles in Discrete Spaces
According to the hypothesis that the universe is discrete, the elementary particles are structures built around world points with a given symmetry. Let us recall that the cosmic bits of a world point are all connected to each other through ferromagnetic interactions [1] . Then space-time disappears inside a world point which therefore seems punctual from an experimental point of view. According to [3] the size 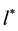 of a world point would be of the order of
of a world point would be of the order of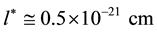 .
.
Our approach suggests that a particle could be structured along a three levels organization
1) A particle is built around a special world point (whose size is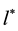 ), called its seed. The internal interactions matrix of the seed GP must transform according to gauge symmetries and the symmetry properties of the seed determine the symmetry of the whole particle.
), called its seed. The internal interactions matrix of the seed GP must transform according to gauge symmetries and the symmetry properties of the seed determine the symmetry of the whole particle.
2) The seed modifies the polarization states of the neighbouring world points over a range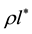 . This region of influence is called the core of the particle and the system made of a seed and its core constitutes a bare particle.
. This region of influence is called the core of the particle and the system made of a seed and its core constitutes a bare particle.
3) Finally the bare particle is surrounded by a cloud of gauge particles whose nature and properties are determined by the symmetry of the seed according to the gauge symmetry mechanisms that have been discussed in [3] . The system made of a bare particle and its cloud of virtual particles constitutes a dressed particle.
2.2. The Irreducible Representations of S4
The permutation group S4 of four objects, a finite group, plays a prominent role in our approach as already stressed in [1] - [3] . Physics, indeed, must be invariant under any permutation of the four axes used to describe the internal states 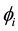 of world point i since no specific orientation of axes can be defined inside a world point. The permutation group S4 of four objects has 24 elements distributed into 5 classes. The table of characters of S4 may be found in [1] . The internal interactions matrices GP of the seed must commute with any four dimensional representation of group S4. Therefore it must transform according to direct sums of irreducible representations of S4. There are two types of irreducible representations. On the one hand
of world point i since no specific orientation of axes can be defined inside a world point. The permutation group S4 of four objects has 24 elements distributed into 5 classes. The table of characters of S4 may be found in [1] . The internal interactions matrices GP of the seed must commute with any four dimensional representation of group S4. Therefore it must transform according to direct sums of irreducible representations of S4. There are two types of irreducible representations. On the one hand 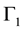 and
and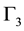 , that are insensitive to mirror operations that is to an odd number of permutations. On the other
, that are insensitive to mirror operations that is to an odd number of permutations. On the other 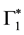 and
and 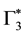 are sensitive to mirror operations. Finally
are sensitive to mirror operations. Finally 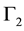 does not take the mirror operations into account. We see below that the particles imply the representations
does not take the mirror operations into account. We see below that the particles imply the representations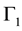 ,
, 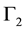 and
and 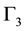 and the antiparticles the representations
and the antiparticles the representations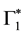 ,
,  and
and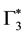 . The problem of finding four-dimensional matrices GP as direct sums of
. The problem of finding four-dimensional matrices GP as direct sums of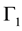

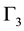
a) 4 = 1 + 3
b) 4 = 2 + 2
c) 4 = 1 + 1 + 2
d) 4 = 1 + 1 + 1 + 1
The matrices GB that transform along to solution a), that is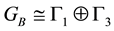

2.3. Recovering the Organization of the Standard Model of Particles
2.3.1. Particles
Super-symmetry theory (Susy) puts forward that fermions and bosons may be considered as two aspects of the very same objects. In a spirit close to that of Susy it is proposed here that the fundamental particles are objects that associate world points with different symmetries. A bare particle would, accordingly, be made of a pair of coupled world points, one undergoing a fermionic polarization and the other a bosonic polarization. The idea that an elementary particle could be formed of a couple of bosonic and fermionic sub-particles has also been suggested by Koide [4] and is implicit, through the 
The state of a particle is then represented in a 16-dimensional vector space that is obtained by the direct product of the two 4-dimensional spaces associated with the members of the pair that form the particle. The states must therefore transform as
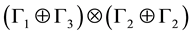
that may be expanded along
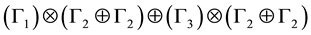
There are therefore four particles. The two particles associated with 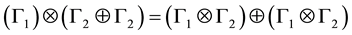


2.3.2. Antiparticles
We now consider how antiparticles may be derived from the same formalism. The different types of particles have been determined by using the mirror insensitive representations 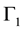


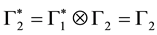
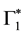
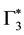


C is the charge conjugation operator.
Let us remember that the polarization 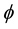
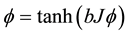
J is the amplitude of binary interactions between the n cosmic bits of a world point and b is a parameter that materializes a cosmic disorder (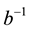
If 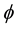

The states of anti-particles then transform as
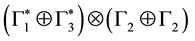
that may be expanded along
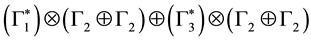
Antiparticles are therefore organized exactly as particles. They have exactly the same properties as the corresponding particles, except for the sign of electric charges which is sensitive to charge conjugation.
We have so far obtained a description of the organization of one family of elementary particles that exactly fits the standard model of particles. However there are three families of particles with identical properties except for their masses. The symmetry properties are the same for the three families and one must admit, accordingly, that the matrices GP are the same for the three families. However while the particles of the first family are stable the particles belonging to the other families are unstable. Therefore, the existence of these families cannot be looked for in some new type of symmetry similar to 
2.3.3. A Non-Standard Family of Particles
According to solution (c): (4 = 1 + 1 + 2) the internal interactions matrix would transform according to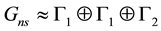
The particles that possibly emerge from this representation have been ignored so far. We consider that 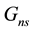
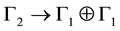


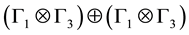
and two fermions:


It is possible that one of these particles corresponds to the particle recently observed at the Large Hadron Col- lider (LHC). To understand which particle is really at stake we must, however, gain much more information re- garding the properties of the found particle.
The two scalar bosons, if they do exist, behave as Higgs scalar particles and could be involved in the same sorts of reactions. If a Higgs boson is defined as a scalar boson the proposed particles are Higgs bosons. If a Higgs boson is defined as a particle that gives masses to otherwise zero mass particles the two particles are not Higgs bosons because, as we will see in the present approach, no Higgs mechanism is necessary to give masses to particles. The lepton could give rise to a new type of neutrino. There are experimental evidences for the exis- tence of a new type of neutrino, called a sterile neutrino, whose (still controversial) existence has possibly been revealed in LSND [5] or Mini-Boone experiments [6] .
Finally we can ignore the representation 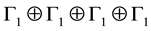
3. On Particles Masses
3.1. General Considerations
Let us recall that the state 
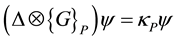
The mass 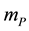
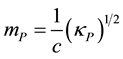
This way of introducing particle masses seems to go against the usual conclusion that all particles must have zero masses due to the dichotomy of the universe between a right 
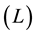
The mass term in the Lagrangian of a fermion field 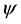
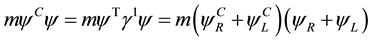
We consider the right handed term




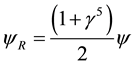
Since 

and thus
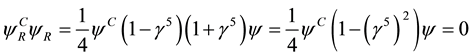
Likewise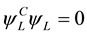
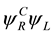
If there is no universe dichotomy this derivation no longer holds and the particles may have non zero-masses.
The universe dichotomy is introduced to account for the experimental observation that the neutrinos are left handed. We show in Section 4.1 that this property of neutrinos is, in reality, a consequence of the model and no Higgs mechanism is needed to give a mass to particles. It must be stressed, however, that a Higgs scalar field, identified with the world point polarization state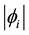
3.2. Seeds Masses
The states 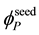
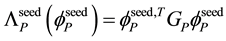
under the constraint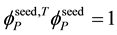

The mass 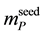
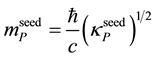
3.2.1. Bosonic Seeds
Since the internal interaction matrix GB of bosonic seeds must transform according to the direct sum

The analytical form of matrix GB may be found from the dynamics of boson fields that is from the Klein- Gordon equation

by isolating a world point i from its neighbourhood. This is achieved by replacing the differential operators 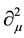

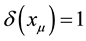
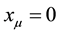
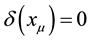

GB, therefore, is proportional to the metric matrix of vacuum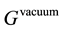
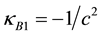
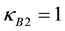
3.2.2. Fermionic Seeds
Since the internal interaction matrix GF of fermionic seeds must transform according to the direct sum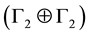

The analytical form of matrix GF may be found from the equation of fermion fields that is from the Dirac equation
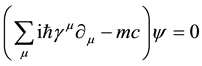
by isolating a world point i from its neighbourhood. Then
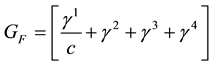
The Dirac matrices 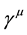
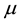
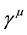
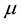
is introduced so as to make hermitian the operator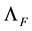

and the matrix GF finally writes
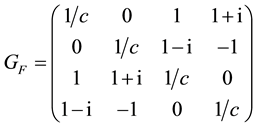
As expected GF has two real two-fold degenerate eigenvalues 
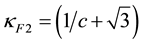
The lepton associated with the eigenvalue 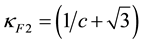
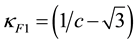
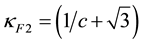
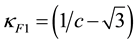

3.3. Masses of Bare Particles
By using a first order perturbation expansion we find that the eigenvalue 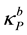
Proof:
A bare particle, we have seen in Section 2.1, is comprised of a seed and its core. Let i be the label of world points belonging to the core. The vacuum states 
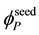
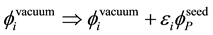
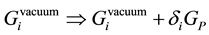
The eigenvalue 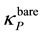
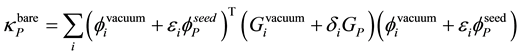
There is no orientation correlations between 
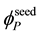
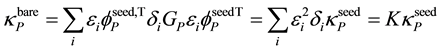
3.4. Analytical Expressions for Bare Particles Masses
The Lagrangian operator of a particle, that is of a coupled pair of world points, one of bosonic type, the other of fermionic type, must keep the symmetry properties of the two components taken separately so as to preserve the organization of the particles of the Standard Model. This compels the Lagrangian to be a 16-dimensional operator given by
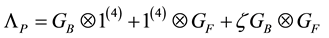


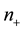
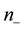
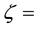
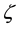




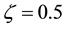

The Lagrangian (4) has four eigenvalues. The first is associated with the bare down quark
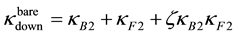
The second is associated with the bare up quark

That is
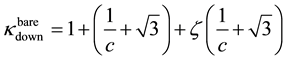
and
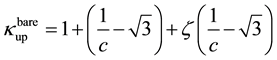
Since the masses of bare particles are proportional to the masses of their seeds one has
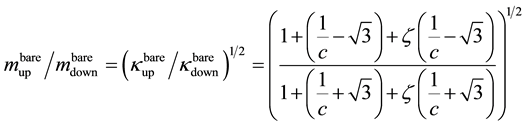
For leptons, however, no calculation of bare particles has been carried out. It is then necessary to add the effects of virtual bosons. Then to calculate their dressed masses one must write
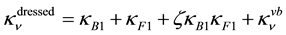
for the neutrino 
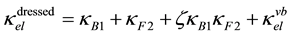
for the electron. Explicitly one has
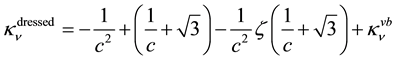
and
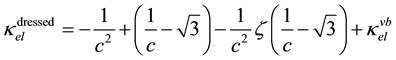
3.5. The Zitterbewegung
The definition of the bare mass 




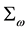
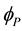



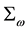
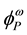
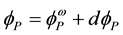
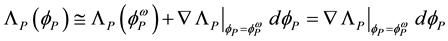
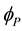

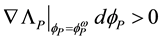

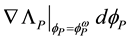



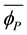
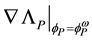



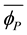
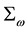

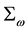

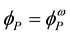
The mass of a dressed particle 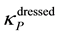
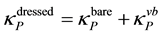


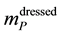
3.6. Numerical Calculations and Comparison with Experimental Observations
There is no direct measurement of quark bare masses because it is not possible to observe separate quarks due to their confinement properties. The value of separate bare quark masses can only be obtained through various theoretical calculations that usually lead to different numerical values. The results for quarks bare masses are rather scattered. For example it has been proposed [7] that

Calculations, carried out on lattices by C. Davies et al. [8] (see also [9] ) give values for the bare masses of light quarks that, the authors claim, are much more accurate than the previously published data. They find
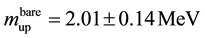
which gives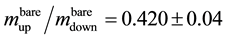
The ratio between bare quark masses is better determined than their explicit values and this is the only value that one can calculate in the present theory without appealing to free parameters. There are two parameters in eq. (9): c and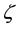

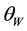
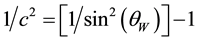
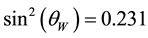
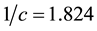

With the value 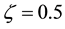
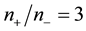
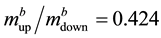
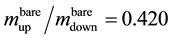
The range of values given by Davies calculation is 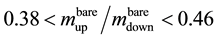
The average value 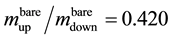

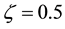
With the values adopted for c and 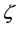
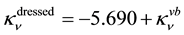


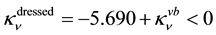
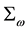

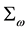
4. Other Considerations
4.1. The Neutrino Left Handed Chirality
The discovery (by Wu) that the parity symmetry is completely broken by weak interactions and that the electronic neutrino is left handed compelled the physicists to assume that the universe is, in actual fact, made of two different sorts of universes: a left-handed universe L and a right-handed universe R. This hypothesis, we have seen, leads to the conclusion that all fermions are zero-mass particles. The eigenvalue associated with neutrinos is negative 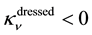
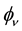
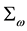
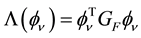
with
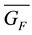
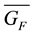
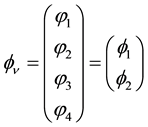
For 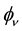

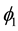

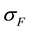
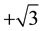
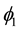
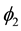
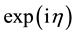
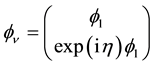
The Lagrangian of a neutrino then writes
that is

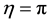

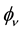
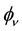

The eigenvalue associated with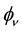
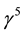
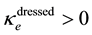
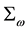
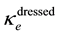
The particles masses can be computed without appealing to a Higgs mechanism as we have seen. We have already said that the Higgs field, identified with the polarization amplitude 
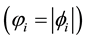
The model can however yield a value for the mass 


where
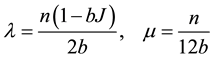
The minimum 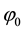

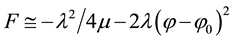
that is
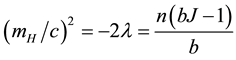
In other respect one has 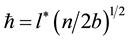
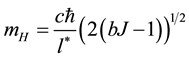
We now give to c its physical value. With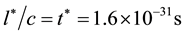

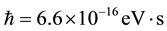
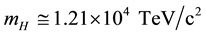
a value that is far out of reach even for the most modern colliders.
4.2. Regge Trajectories
The model presented here also provides a very simple explanation of Regge trajectories [10] . We have seen that the eigenvalue 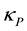

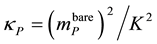
Let us gather 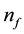


that is
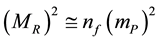
Finally
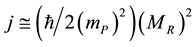
This linear dependence of the spin j along the square of the mass 
4.3. The CPT Theorem
The parity symmetry P is broken by weak interactions as we have seen. On can wonder whether the time inversion symmetry T, or the charge conjugation symmetry C can also be broken. We do not know the answer but a very general property, the CPT theorem, a product of these three invariance shows that the product CPT must be always verified.
The vector
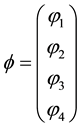
represents the state of a particle. The state 
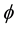

C is the charge conjugation operator.
In other respects the time reversal operator T changes the sign of the time component 
that is

Finally the operation of reversing the direction of one axis, say the 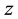
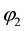
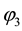
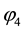

that is
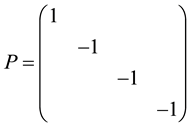
We see that
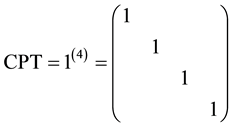
a simple and straightforward derivation of the CPT theorem.
4.4. On Electric Charges of Fermions
The electric charge Qf of a given fermion, lepton or quark, is derived from the hypercharge Yf through the formula
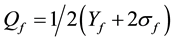
where 
The three generators of 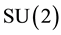
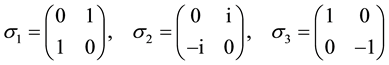
The interaction Lagrangian between leptons and their gauge field writes [3]
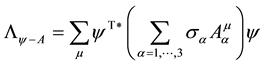
The quantities 
is added (and substracted) to the list of Pauli matrices (as in GWS theory)
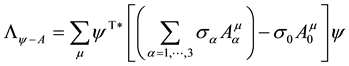
The amplitude of the hypercharge 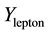

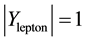
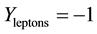

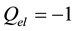
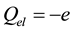


Let us now turn towards the electric charges of quarks. The eight generators of SU(3) are the eight Gell-Mann matrices

To make the expression of the Lagrangian more symmetric the 3-dimensional identity matrix
is added (and substracted) to the list of Gell-Mann matrices
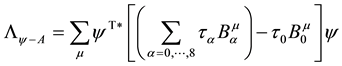
In order to compare the electric charges of leptons and quarks it is necessary to establish an endomorphism between the set of the eight Gell-Mann matrices and the set of three Pauli matrices. This endomorphism is given by
in the main term and 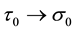
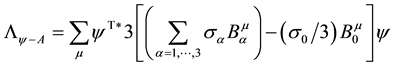
One observes that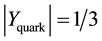
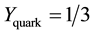

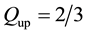
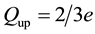
The isospin of the down quark is

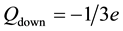
4.5. Three Families of Particles
As already argued, the symmetry properties of bare particles are determined by the matrix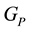
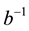
We have seen, in [1] , that the dimensionality d of space-time is given by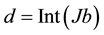

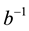
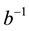
1)
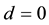
2)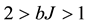
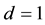
3)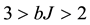
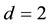
4)
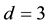
5)
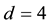
The three domains (3, 4 and 5) of cosmic temperatures would correspond to the three families of particles. The domain (5) 
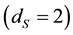

4.6. On the CKM Matrix
The idea that the three-fold multiplicity of families of particles may be explained by a dimensional re-organiza- tion of space-time in the core of a particle is supported by the following analysis of the CKM (Cabbibo, Kobayashi and Maskawa) matrix.
The CKM matrix V describes the amplitudes of transition probabilities between the set of three quarks with isospin −1/2, namely u, c and t, and the set of three quarks d, s and b, with isospin +1/2 through weak interaction. The CKM matrix V writes

The experimental values of the elements of the CKM matrix are given below in Equation (15).
Here we strive to find the CKM matrix by using a very simple geometrical argument. The probability 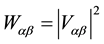
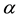

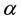
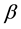


The perturbation 
with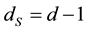
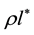
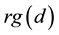
For 3-dimensional quarks (u and d) one has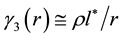

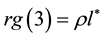
For 2-dimensional quarks (s and c) one has
and, therefore,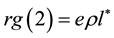

Finally for 1-dimensional quarks (t and b) one has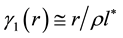


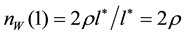
According to our hypothesis, the probability 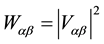
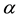
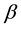
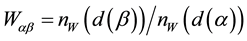
That is
and
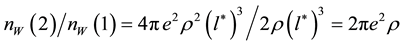
The matrix W then writes
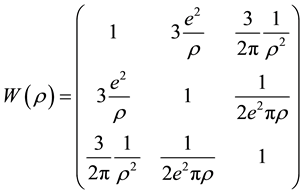
Since one must have 

Finally the transition probability amplitude is given by


One finds

to be compared with the experimental matrix [10]

The agreement is not that satisfactory, especially for the transitions between the quarks of muon family and those of tau family. This is not surprising given the crudeness of the calculations. One may consider, however, that the general trend is in the right direction and that the approach brings a valuable support to the granular structure of space-time and to the thermodynamic interpretation of the nature of fermions families. With the value 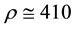
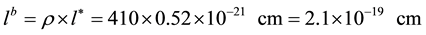
perhaps not completely out of the reach of realizable colliders.
5. Conclusions
The details of the organization of particles along the Standard model, their spins, charges and masses have been recovered in the framework of the discrete spaces model that we put forward. The neutrino chirality has been explained without appealing to a dichotomy between left and right universes. The introduction of this dichotomy is, in our opinion, a price too high to pay.
Our approach of physical phenomena implies a number of consequences:
1) The concept of infinity does not belong to the realm of physics. Infinity would only be a creation of mathematicians. We know that the observable universe is finite and therefore the infinitely large cannot be observed. We assume that, likewise, the infinitely small cannot be observed either.
2) The set of experimental results accumulated so far is enough to build a comprehensive theory of natural phenomena.
3) Many physicists believe that we cannot understand the laws of nature without appealing to complicated mathematics. Some physicists even believe that the necessary mathematics must be so complicated that they are outside the reach of a human brain. We do not share this prejudice. Notions of linear algebra and elements of group theory seem to be enough.
Finally let us list the main notions that have been introduced and that could be open to experimental observations.
a) First of all, we have introduced a metric limit 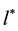

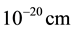
b) We have defined a so-called cosmic noise, a sort of temperature that describes the disorder of the most elementary physical systems (the cosmic bits) at a Planck scale. The cosmic noise, in our model, plays a central role in the organization and understanding of all natural phenomena. This noise could possibly be observed through phenomena relating to dark matter [3] or, perhaps, to the properties of quasars. The maps of dark matter would be, in reality, maps of cosmic noise.
c) The model has no need of a dichotomy of the universe between a right and a left universe. The left handedness character of a neutrino is a consequence of the present theory and no Higgs mechanism is necessary to give a mass to particles. The mass of the Higgs particle, if any, would be of the order of 104 TeV.
d) The model opens the possibility to the existence of a non-standard family of particles whose main properties are described in Section 5.
Finally we, obviously, do not claim that the model of discrete spaces could be a sort of Grand Unified Theory (GUT), but we simply hope that some significant steps have been made towards the solution of the sixth Hilbert’s problem [11] [12] , which is the expression of axioms of physics. We could also say that, since it gives a physical interpretation to so many natural phenomena, the model of discrete spaces that we put forward probably contains some elements of reality.
Acknowledgements
I would like to express my best thanks to two institutions and to their managers. The first is the French Atomic Commission (CEA) with Dr Jacques Chappert who accepted that I spend one year learning high energy physics as an ordinary student at the Marseilles-Luminy University. He also accepted that I work on the subject for so long a time with so few published material. The other is the National Scientific Research Centre (CNRS) with Dr Bart van Tiggelen and Franck Hekking who welcomed me as an external researcher in their laboratory. Finally I thank my friend Pr Roger Maynard, my daughter-in-law Dr Ana Cabral and, obviously, my wife Michèle who incited me not to give up.
References
- Peretto, P. (2014) Journal of Modern Physics, 8, 563-575.
- Peretto, P. (2014) Journal of Modern Physics, 14, 1370-1386.
- Peretto, P. (2014) Journal of Modern Physics, 18, 2049-2062.
- Koide, Y. (1983) Physical Review D, 28, 252. http://dx.doi.org/10.1103/PhysRevD.28.252
- Dodelson, S., Melchiorri, A. and Slosar, A. (2006) Physical Review Letters, 97, Article ID: 04301.
- Aguilar, A. (2010) Physical Review D, 81, 098.
- Testa, M. (1975) Physics Letters B, 56, 53-56.
- Davies, C. (2013) Physical Review D, 81, 1103.
- Daum, M., et al. (2000) Physical Review Letters, 85, 1815.
- Collins, P.D.B. (1997) An Introduction to Regge Physics and High Energy Physics. Cambridge University Press, Cambridge.
- Nakamura, K., et al. (2010) Journal of Physics G: Nuclear and Particle Physics, 37, Article ID: 075012. http://dx.doi.org/10.1088/0954-3899/37/7A/075021
- Corry, L. (1994) Archives of History of Exact Sciences, 51, 83-168. http://dx.doi.org/10.1007/BF00375141