Journal of Modern Physics
Vol.06 No.05(2015), Article ID:55725,11 pages
10.4236/jmp.2015.65066
Theoretical Calculation of the Low-Lying Electronic States of the Molecule BaS
Sally Shawa1, Mahmoud Korek1*, Ghassan Younes1, Nayla El-Kork2
1Faculty of Science, Beirut Arab University, Beirut, Lebanon
2Khalifa University, Sharjah, United Arab Emirates
Email: *fkorek@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 January 2015; accepted 15 April 2015; published 16 April 2015
ABSTRACT
Complete Active Space Self Consistent Field (CASSCF) with Multireference Configuration Interaction (MRCI) and Rayleigh-Schrödinger Perturbation Theory (RSPT2-RS2) methods have been used to investigate the potential energy curves for the 12 low-lying singlet and triplet electronic states in the representation 2s+1Λ(+/−) of the molecule BaS with Davidson corrections. The harmonic frequency we, the internuclear distance Re, the electronic energy with respect to the ground state Te, the rotational constants Be and the permanent dipole moment have been calculated for these elec- tronic states. The eigenvalues Ev, the rotational constants Bv, the centrifugal distortion constant Dv and the abscissas of the turning points Rmin and Rmax have been investigated using the canonical functions approach. Nine new electronic states have been investigated here for the first time. The comparison between the values of the present work and those available in the literature for several electronic states shows a good agreement.
Keywords:
Ab Initio Calculation, Electronic Structure, Spectroscopic Constants, Potential Energy Curves, Dipole Moments, Vibration-Rotation Calculation

1. Introduction
Examining the bonding of Alkaline earth sulfides molecules has been of both experimental and theoretical interest because of their promising variety of scientific areas including catalysis, biochemistry, material science [1] [2] , astrophysical applications [3] [4] and its significant role in the electronic transition chemical laser [5] - [7] . Barium sulfide BaS is one of the Alkaline earth sulfides that have been first obtained in 17th century by the reduction of the powder of barite BaSO4 with charcoal at high temperature [8] . Recently metal sulfide nanomaterials have attracted great attention because of their excellent properties and promising applications in electronic, optical and optoelectronic devices. Well-aligned nanostructure arrays on substrates are highly attractive for their enhanced properties and novel applications.
The rotational transitions of the main barium sulfide isotope have been recorded by Tiemann et al. [9] . In order to obtain the dipole moment for this molecule Melendres et al. [10] accomplished radio frequency Stark measurements of the J = 1 rotational level. The absorption band system of the molecule BaS has been determined by Clements and Barrow [11] . Helms et al. [12] measured the millimeter-wave spectra of six isotopic species of BaS in the frequency range 55 - 339 GHz which allows the determination of Dunham coefficients. Additional measurements of the pure rotational spectrum of BaS in the range 358 - 394 GHz were recorded [13] . Recently, Janczyk and Ziurys performed a pure rotational study of BaS in the frequency range of 355 - 396 GHz [13] . High resolution laser excitation spectra of the A1Π - X1Σ+ and a3Π - X1Σ+ electronic transitions in the 12,100 - 12,765 cm−1 spectral region were reported [14] . Rotational analysis of the electronic transitions B1Σ+ - X1S+ has been done with the calculation of the molecular constants for each state. It was noticeably difficult to determine those constants for the electronic state A1Σ+, as it showed numerous perturbations [15] .
The absence of theoretical calculation of higher excited states of the molecule BaS stimulate us to investigate, in the present work, more extensive ab initio calculation of barium sulfides molecule. Based on our previous theoretical calculations [16] - [24] , the potential energy curves and spectroscopic constants of the low lying 12 singlet, and triplet electronic states have been calculated where 9 electronic states have been investigated here for the first time. The transition energy with respect to the minimum energy for the ground state Te, the equilibrium internuclear distance Re, the harmonic frequency we, the rotational constant Be, and the permanent dipole moment have been calculated for the considered electronic states of this molecule. Taking advantage of the electronic structure of the investigated electronic states of the molecule BaS and by using the canonical functions approach [25] - [27] , the eigenvalue Ev, the rotational constant Bv, and the abscissas of the turning points Rmin and Rmax have been calculated for several vibrational levels of the considered electronic states.
2. Method of Calculations
In the present work we investigated the low-lying singlet and triplet electronic states of the molecule BaS using complete active space self-consistent field (CASSCF) procedure followed by a multireference configuration interaction (MRCI with Davidson correction) treatment for the electron correlation and Rayleigh-Schrödinger Perturbation Theory (RSPT2-RS2). The entire CASSCF configuration space was used as the reference in the MRCI calculations, which were done via the computational chemistry program MOLPRO [28] taking advantage of the graphical user interface GABEDIT [29] . The Barium species is treated as a system of 56 electrons by using the ECP46MWB basis set for s, p, and d functions (with 46 core electrons). The 16 electrons of the sulfide atom are considered using the Rydberg5 basis set for s, p and d functions. Among the 26 electrons explicitly considered for BaS (10 electrons for Ba and 16 for S) 22 inner electrons were frozen in subsequent calculations so that four valence electrons were explicitly treated, corresponding to 16 active orbitals. All computations were performed in the C2v symmetry.
3. Results and Discussion
The potential energy curves (PECs) for the 12 singlet and triplet electronic states, in the representation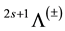 , of the molecule BaS were generated using the MRCI for 105 internuclear distances calculations in the range 1.9092Ǻ ≤ Re ≤ 4.9992 Ǻ (Figure 1, Figure 2)). By fitting the calculated energy values of the different investigated electronic states, into a polynomial in R around the internuclear distance at equilibrium Re, the harmonic vibrational frequencies ωe, the relative energy separations Te, and the rotational constants Be have been calculated. These values with the available data in literature are given in Table 1.
, of the molecule BaS were generated using the MRCI for 105 internuclear distances calculations in the range 1.9092Ǻ ≤ Re ≤ 4.9992 Ǻ (Figure 1, Figure 2)). By fitting the calculated energy values of the different investigated electronic states, into a polynomial in R around the internuclear distance at equilibrium Re, the harmonic vibrational frequencies ωe, the relative energy separations Te, and the rotational constants Be have been calculated. These values with the available data in literature are given in Table 1.
One can notice the small difference between the values of Te for the higher singlet and triplet electronic states. In literature there are fragmented experimental data for 3 lowest electronic states. By using the RSPT2-RS2 method we found that the ground state is (1)1Π, by repeating the calculation with the MRCI technique we found that the ground state is X1Σ+ which is confirmed experimentally. The comparison of our calculated values of Te with the only value available in literature for the electronic state (1)1Π shows an acceptable agreement. While by comparing the available data of Re in literature for 3 electronic states with our investigated values one can find
Figure 1. Potential energy curves of the electronic states 1Σ±, 1Δ and 1Π of the molecule BaS.
Figure 2. Potential energy curves of the electronic states 3Σ±, 3Δ and 3Π of the molecule BaS.
that a very good agreement for the 2 electronic states (1)1Π and (1)3Π with an average relative difference ΔRe/Re = 5.2% and an acceptable agreement for the ground state. For the vibrational frequency we our calculated value is in excellent agreement with that given by Barrow et al. [33] for the electronic state (1)3Π while this agreement becomes acceptable for the 2 electronic states X1Σ+ and (1)1Π. No comparison for the spectroscopic data for the other electronic states since they are given here for the first time.
4. Dipole Moment
The static dipole moment is a fundamental electrostatic property of a neutral molecule, its importance lying in the description of numerous physical phenomena. The expectation value of this operator is sensitive to the nature of the least energetic and most chemically relevant valence electrons. The calculated values of the dipole moments for the considered lowest-lying electronic states are plotted in term of the internuclear distance R in Figure 3, Figure 4. In our calculation we considered the Ba atom at the origin. Since the dipole moment have negative sign for the considered states where R ≥ 2.0592Å the dipole moment vector are directed from S to Ba atom.
Table 1. Spectroscopic constants for the singlet and triplet electronic states of the molecule BaS.
a and b are for present work using respectively MRCI and RSPT2-RS2 methods. cRef. [30] , dRef. [31] , eRef. [32] , fRef. [14] .
Figure 3. Static dipole moment curves of the electronic states 1Σ±, 1Δ and 1Π of the molecule BaS.
5. Vibration-Rotation Calculation
The vibrational calculation of a diatomic molecule is a promising approach for realizing a quantum computer. The vibrational states of these molecules represent the qubits and tailored the femtosecond laser pulses to implement quantum gate operations [30] . These vibrational states of molecules are stable over the time scales of interest, therefore the number of qubits is not limited to ten and by using more vibrational states, it may be possible to represent quantum information units having more than two states |0>, |1>, |2>, |3>・・・ [31] . This vibrational state approach has a number of qubits proportional to the number of vibrational degrees of freedom and more qubits can be realized using a N-atom molecule. Using the canonical functions approach [25] - [27] the radial Schrödinger equation can be replaced by the system of equations
Figure 4. Static dipole moment curves of the electronic states 3Σ+, 3Δ and 3Π and 3Φ of the molecule BaS.
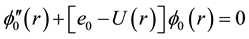 (1)
(1)
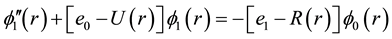 (2-1)
(2-1)
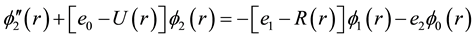 (2-2)
(2-2)
・・・
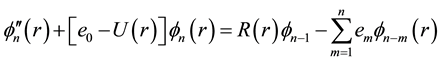 (2-n)
(2-n)
where R(r) = 1/r2, Equation (1) represents the pure vibrational Schrödinger equation and the remaining equations are the pure rotational Schrödinger equations. Once e0 = Ev is calculated, e1 = Bv, e2 = Dv, ××× can be obtained by using alternatively Equations (2-n). By using the cubic spline interpolation between each two consecutive points of the potential energy curves obtained from the ab initio calculation the abscissas of the turning points Rmin and Rmax have been calculated (Table A1 in Appendix). By comparing our calculated values of Bv with those given in literature for the 3 electronic states X1Σ+, (1)1Π, and (1)3Π given in literature [13] -[15] [33] [34] , one can find that, these experimental values are systematically greater than our calculated values by ≈0.02 cm−1 for the ground state and by ≈0.01 cm−1 for the (1)1Π, and (1)3Π states for the investigated vibrational levels. The comparison of our calculated values of Ev with those given in literature [13] -[15] [33] [34] is not possible since the origin of energy in these references is considered at v = 0 while in our calculation this origin is at the minimum of the potential energy curve for each electronic state. But we compared the difference of energy 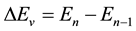 between each 2 consecutive vibrational levels of our calculated values with those given in literature [13] -[15] [33] [34] , we found that this difference varies from one vibrational level to another and depend on the considered electronic state, but an overall good agreement can be considered where the relative difference is 4.5% ≤ ΔEv/Ev ≤ 12%.
between each 2 consecutive vibrational levels of our calculated values with those given in literature [13] -[15] [33] [34] , we found that this difference varies from one vibrational level to another and depend on the considered electronic state, but an overall good agreement can be considered where the relative difference is 4.5% ≤ ΔEv/Ev ≤ 12%.
6. Conclusion
In the present work, an ab initio calculation of 12 singlet and triplet lowest electronic states in the 2s+1Λ± representation has been performed via CASSCF/MRCI methods. The potential energy curves have been calculated along with the spectroscopic constants Te, Re, Be, and ωe for these states and the static dipole moment μ. In literature there is a limited number of data for the investigated values either theoretically or experimentally. The comparison of our calculated values with either the theoretical or the experimental data available in the literature demonstrated an overall good agreement. Nine new electronic states have been investigated here for the first time. The investigated data in the present work may help for more experimental or theoretical studies in the future for higher electronic states.
References
- Kretzschmar, I., Schröder, D., Schwarz, H. and Armentrout, P.B. (2003) International Journal of Mass Spectrometry, 228, 439-456. http://dx.doi.org/10.1016/S1387-3806(03)00137-4
- Armentrout, P.B., Kretzschmar, I., Schröder, D. and Schwarz, H. (2001) International Journal of Mass Spectrometry, 210/211, 283-301. http://dx.doi.org/10.1016/S1387-3806(01)00400-6
- Takano, S., Yamamoto, S. and Saito, S. (1989) Chemical Physics Letters, 159, 563-566. http://dx.doi.org/10.1016/0009-2614(89)87533-5
- Halfen, D.T., Apponi, A.J., M.Thompsen, J. and Ziurys, L.M. (2001) Journal of Chemical Physics, 115, 11131-11138.
- Bernard, D.J., Slafer, W.D., Love, P.J. and Lee, P.H. (1977) Applied Optics, 16, 2108-2115. http://dx.doi.org/10.1364/AO.16.002108
- Field, R.W., Jones, C.R. and Broida, H.P. (1974) Journal of Chemical Physics, 60, 4377-4382.
- Sutton, D.G. and Suchard, S.N. (1975) Applied Optics, 14, 1898-1910. http://dx.doi.org/10.1364/AO.14.001898
- Licetus, F. (2012) Litheosphorus Sive De Lapide Bononiensi Utini: Ex typographia Nicolai Schiratti Bologna. University Library of Bologna, Italy, 1640.
- Tiemann, E., Ryzlewicz, Ch. and Törring, T. (1976) Zeitschrift fur Naturforschung Section A―Journal of Physical Sciences, 31, 128-130.
- Melendres, C.A., Hebert, A.J. and Street Jr., K. (1969) Journal of Chemical Physics, 51, 855-856.
- Clements, R.M. and Barrow, R.F. (1968) Chemical Communications (London), 1408a.
- Helms, D.A., Winnewisser, M. and Winnewisser, G. (1980) Journal of Physical Chemistry, 84, 1758-1765. http://dx.doi.org/10.1021/j100451a003
- Janczyk, A. and Ziury, L.M. (2005) Journal of Molecular Spectroscopy, 236, 11-15. http://dx.doi.org/10.1016/j.jms.2005.11.011
- Li, G., Wang, J.G. and Bernath, P.F. (2012) Journal of Molecular Spectroscopy, 271, 10-14. http://dx.doi.org/10.1016/j.jms.2011.10.003
- Morbi, Z. and Bernath, P.F. (1995) Journal of Molecular Spectroscopy, 171, 210-222. http://dx.doi.org/10.1006/jmsp.1995.1113
- Taher-Mansour, F., Allouche, A.R. and Korek, M. (2008) Journal of Molecular Spectroscopy, 248, 61-65. http://dx.doi.org/10.1016/j.jms.2007.11.012
- Korek, M., Kontar, S., Taher-Mansour, F. and Allouche, A.R. (2009) International Journal of Quantum Chemistry, 109, 236-242. http://dx.doi.org/10.1002/qua.21779
- Hamdan, A. and Korek, M. (2010) Chemical Physics, 369, 13-18. http://dx.doi.org/10.1016/j.chemphys.2010.01.023
- Hamdan, A. and Korek, M. (2011) International Journal of Quantum Chemistry, 111, 2960-2965. http://dx.doi.org/10.1002/qua.22602
- Fahs, H., Korek, M., Allouche, A.R. and Aubert-Frecon, M. (2004) Chemical Physics, 299, 97-103. http://dx.doi.org/10.1016/j.chemphys.2003.12.009
- Badreddine, K., El-Kork, N. and Korek, M. (2012) Journal of Modern Physics, 3, 839-849.
- Fahs, H., Korek, M., Allouche, A.R. and Aubert-Frecon, M. (2002) Journal of Chemical Physics, 117, 3715-3720. http://dx.doi.org/10.1063/1.1493769
- Farhat, A., Korek, M., Marques, M.A.L. and Abdul-Al, S.N. (2012) Canadian Journal of Chemistry, 90, 631-639. http://dx.doi.org/10.1139/v2012-036
- Korek, M., El-Kork, N., Moussa, A.N. and Bentiba, A. (2013) Journal of Chemical Physics Letters, 575, 115-121.
- Kobeissi, H., Korek, M. and Dagher, M. (1989) Journal of Molecular Spectroscopy, 138, 1-12. http://dx.doi.org/10.1016/0022-2852(89)90092-1
- Kobeissi, H. and Korek, M. (1992) Journal of Computational Chemistry, 13, 1103-1108. http://dx.doi.org/10.1002/jcc.540130909
- Korek, M. (1999) Computer Physics Communications, 119, 169-178. http://dx.doi.org/10.1016/S0010-4655(98)00180-5
- Werner, H.J., Knowles, P.J., Lindh, R., Manby, F.R., Schütz, M., Celani, P., Korona, T., Rauhut, G., Amos, R.D., Bernhardsson, A., Berning, A., Cooper, D.L., Deegan, M.J.O., Dobbyn, A.J., Eckert, F., Hampel, C., Hetzer, G., Lloyd, A.W., McNicholas, S.J., Meyer, W., Mura, M.E., Nicklaß, A., Palmieri, P., Pitzer, R., Schumann, U., Stoll, H., Stone, A.J., Tarroni, R. and Thorsteinsson, T. (2009) MOLPRO Is a Package of ab initio Programs. http://www.molpro.net/info/molpro2006.1/molpro_manual
- Allouche, A.R. (2011) Journal of Computational Chemistry, 32, 174-182. http://dx.doi.org/10.1002/jcc.21600
- Tesch, C.M., Kurtz, L. and de Vivie-Riedle, R. (2001) Chemical Physics Letters, 343, 633-641. http://dx.doi.org/10.1016/S0009-2614(01)00748-5
- Mishima, K., Tokumo, K. and Yamashita, K. (2008) Chemical Physics, 343, 61-75. http://dx.doi.org/10.1016/j.chemphys.2007.10.027
- Zhao, M. and Babikov, D. (2006) Journal of Chemical Physics, 125, 24105-24111. http://dx.doi.org/10.1063/1.2220039
- Barrow, R.F., Burton, W.G. and Jones, P.A. (1970) Physical Chemistry Laboratory, Oxford University. http://pubs.rsc.org
- Cummins, P.G., Eield, R.W. and Renhorn, I. (1981) Journal of Molecular Spectroscopy, 90, 327-352. http://dx.doi.org/10.1016/0022-2852(81)90131-4
Appendix
Table A1. Values of the eigenvalues Ev the rotational constants Bv, and the abscissas of the turning points Rmin and Rmax for the different vibrational levels of X1Σ+, (1)1Π, (1)3Σ+, (1)3Π, and (3)3Π states of the BaS molecule.
NOTES
*Corresponding author.







