Journal of Modern Physics
Vol.06 No.02(2015), Article ID:54195,7 pages
10.4236/jmp.2015.62022
Cell Gas Free Energy as an Approximation of the Continuous Model
Vira A. Boluh1, Alexei L. Rebenko2
1Faculty of Mathematics, Zhytomyr, Ukraine
2Institute of Mathematics, Ukrainian National Academy of Sciences, Kyiv, Ukraine
Email: virashevchuk@ukr.net, rebenko@imath.kiev.ua
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 February 2015; accepted 15 February 2015; published 25 February 2015
ABSTRACT
A continuous infinite system of point particles interacting via two-body strong superstable potential is considered in the framework of cell gas (CG) model of classical statistical mechanics. We consider free energy of this model as an approximation of the correspondent value of the continuous system. It converges to the free energy of the conventional continuous gas if the parameter of approximation 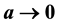 for any values of an inverse temperature
for any values of an inverse temperature  and volume per particle
and volume per particle .
.
Keywords:
Strong Superstable Potential, Quasi-Lattice Approximation, Cell Gas

1. Introduction
One of the most important mathematical problem of statistical mechanics is description of the gas-liquid phase transition within the framework of standard model of 2-partical Lenarda-Johnson type intermolecular interaction. The presence of phase transition at some temperature 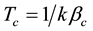 (
( is the Boltzmann constant,
is the Boltzmann constant, 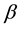 is inverse temperature in units of inverse energy) means that at
is inverse temperature in units of inverse energy) means that at 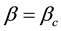 in some interval of change of density
in some interval of change of density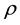 , pressure
, pressure 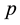 does not depend on density or a specific volume of
does not depend on density or a specific volume of 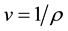 (see, for example [1] ). Taking into account the well-known thermodynamics formulas it means that free energy of the system depends on specific volume
(see, for example [1] ). Taking into account the well-known thermodynamics formulas it means that free energy of the system depends on specific volume 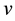 linearly in the indicated interval of change of density. This result was obtained as early as the end of 60th for the lattice gas model in the articles of F. A. Berezin and Ya. G. Sinai [2] for unpositive potentials and R. L. Dobrushin [3] for more general potentials of interaction.
linearly in the indicated interval of change of density. This result was obtained as early as the end of 60th for the lattice gas model in the articles of F. A. Berezin and Ya. G. Sinai [2] for unpositive potentials and R. L. Dobrushin [3] for more general potentials of interaction.
However, the lattice gas is some kind of “toy” model which is very far from the real continuous system. The model of cell-type gas, which actually is the model of the continuous system of point particles and differs from the standard model of gas only by determination of the phase (configuration) space, was offered in recent work [4] of one of the authors of this article.
Cell gas in 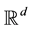 is a continuous gas but its space of configurations is arranged so that for a given partition
is a continuous gas but its space of configurations is arranged so that for a given partition 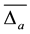 of
of 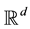 into elementary hiper-cubes
into elementary hiper-cubes 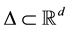 with a rib
with a rib 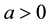 there is no more then one point particle in each cell (cube). These particles move in
there is no more then one point particle in each cell (cube). These particles move in 


Why do we need this result? In the article [4] it was shown that it was possible to introduce an approximation of the interaction potential in such a way that the cell gas model grows into the model of the lattice gas on the lattice

2. Notations and Main Results
2.1. Configuration Space
Let 




where 





and

By 







and hence as a measure 

Define the Lebesgue-Poisson measure 


The restriction of 





Let 



We will write 











Then for any 


and

Definition 2.1. Infinite system of point particles in 


For detail structure of this model see [4] .
2.2. Definition of the System
We consider a general type of two-body interaction potential

(A): Assumption on the interaction potential. Potential 








where

The potentials of this type are strong superstable.
Definition 2.2. Interaction is called strong superstable (SSS), if there exist





Remark 2.1. Superstable interactions were introduced by D. Ruelle (see [11] or [12] , Ch. 3.2.9 and [10] ). Y. M. Park (see [14] ) was the first, who used the condition (12) with 

One of the most popular example which is used in molecular physics is Lenard-Jonson potential:

where constants
Figure 1. The typical behavior of the potentials. (14)
Remark 2.2. For the potentials which are considered in this article (see (9)-(11)) the corresponding con- stants 


where

See for the proof [13] .
2.3. Partition Functions, Free Energy and Pressure
The main physical characteristics of the system are determined by thermodynamic potentials that associated with small and grand partition functions by the following formulas: 1) free energy

where limit is done in such a way that volume per particle



2) pressure

where 

The correspondent values for cell gas model are defined by the same formulas but with help of partition functions(see Definition 2.1):

and

where

Remark 2.3. The product of functions 





Now, we can formulate the main result of the paper.
Theorem 1 Suppose that the interaction potential 



for any


Theorem 2 Suppose that the interaction potential 



holds for all positive 

3. The Proof of the Main Results
The proof of the Theorem 2.1 is the same as the corresponding proof of such theorem for 

To prove the Theorem 2.2 we insert the unite

where


and


Separating the first term of the expansion which corresponds to the value 

where

The Equation (31) gives:


To estimate the second term in (33) we split the energy 

where

and use SSS inequality (12). Then

where

We denote the integral in (32) (after estimating (37)) by the letter 


Every set in 














to the variables 

respect to permutations of variables 











To estimate the ratio of the partition functions in (40) we use the following lemma.
Lemma 1 Suppose that the interaction potential 


for any


Proof. Let us fix some 



with any 



with


where


and chose the 


Then, taking into account that for

and

we obtain:

Holder’s inequality to (49) with respect to probability measure 

Using the property (9) and definition (42) we have:

Using this inequality and taking into account that 

Taking into account that 

with
Now, the proof of the Theorem 2 follows from the trivial estimates of the combinatorial sums in (40). Let for simplicity 



with

It is clear from the Equations (15), (16), (38) that

so, this gives the proof of the main result. □
4. Conclusion
The main result of the article is presented by the Theorem 2.2. It proves that all thermodynamics properties of the infinite system which is defined by phase space (2.1) and interaction potential (2.9) - (2.11) can be described by the cell gas model, phase space and thermodynamics descriptions which are determined by the formulas (2.7), (2.22) - (2.25). In other words, this model approximates the statistical continuous system of interacting point particles up to any preassigned accuracy. It is needed to mark another surprising fact that the set 

Acknowledgements
We thank the referee for valuable remarks which improved the original version. The authors gratefully acknowledge the financial support of the Ukrainian Scientific Project “Investigation of the spectral characteristics and critical behavior of complex systems of mathematical physics” (2011-2015).
References
- Huang, K. (1963) Statistical Mechanics. John Wiley and Sons, Inc., London.
- Berezin, F.A. and Sinai, Ya.G. (1967) Transactions of the Moscow Mathematical Society, 17, 197-212.
- Dobrushin, R.L. (1967) Berk. Sym. Mat. Stat. Prob., VII, 73-87.
- Rebenko, A.L. (2013) Reviews in Mathematical Physics, 25, 1-28.
- Rebenko, A.L. and Tertychnyi, M.V. (2007) Proc. Inst. Math. NASU, 4, 172-182.
- Rebenko, A.L. and Tertychnyi, M.V. (2009) Journal of Mathematical Physics, 50, 0333301-033310. arXiv:0901.0826
- Petrenko, S.M., Rebenko, A.L. and Tertychnyi, M.V. (2010) Ukrainian Mathematical Journal, 63, 425-440. arXiv:1007.4325
- Albeverio, S., Kondratiev, Yu.G. and Röckner, M. (1998) Journal of Functional Analysis, 154, 444-500. http://dx.doi.org/10.1006/jfan.1997.3183
- Rebenko, A.L. (2014) Proc. Inst. Math. NASU, 11, 257-315.
- Ruelle, D. (1970) Communications in Mathematical Physics, 18, 127-159. http://dx.doi.org/10.1007/BF01646091
- Ruelle, D. (1963) Helvetica Physica Acta, 36, 183-197.
- Ruelle, D. (1969) Statistical Mechanics (Rigorous Results). W.A. Benjamin, Inc., Amsterdam.
- Rebenko, A.L. and Tertychnyi, M.V. (2008) Methods of Functional Analysis and Topology, 14, 287-296.
- Park, Y.M. (1984) Communications in Mathematical Physics, 94, 1-33. http://dx.doi.org/10.1007/BF01212347
- Dobrushin, R.L. (1964) Teoriya Veroyatnostei i ee Primeneniya, IX, 626-643.
- Dobrushin, R.L. and Minlos, R.A. (1967) Teoriya Veroyatnostei i ee Primeneniya, XII, 595-618.







